PENGGUNAAN TEORI GRAPH DALAM PERHITUNGAN KOEFISIEN
KORELASI RANK KENDALL (
SKRIPSI
OKTAVIA BR TARIGAN
090823075
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PENGGUNAAN TEORI GRAPH DALAM PERHITUNGAN KOEFISIEN
KORELASI RANK KENDALL (
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
OKTAVIA BR TARIGAN
090823075
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : PENGGUNAAN TEORI GRAPH DALAM
PERHITUNGAN KOEFISIEN KORELASI RANK KENDALL (
Kategori : SKRIPSI
Nama : OKTAVIA BR TARIGAN
Nomor Induk Mahasiswa : 090823075
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (MIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, 22 Juni 2011
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs.Pasukat sembiring , M. Si Drs.Ujian Sinulingga, M. Si NIP. 195311131985031002 NIP. 195603031984031004
Diketahui /Disetujui oleh
Departemen Matematika FMIPA USU
Ketua,
Prof. Dr. Tulus, M.Si
PERNYATAAN
PENGGUNAAN TEORI GRAPH DALAM PERHITUNGAN KOEFISIEN KORELASI RANK KENDALL (
SKRIPSI
Saya mengakui bahwa skripsi ini hasil kerja saya sendiri, kecuali beberapa kutipan
dan ringkasan yang masing – masing disebutkan sumbernya.
Medan, juni 2011
Oktavia Br Tarigan
PENGHARGAAN
Puji dan syukur penulis ucapkan kepada Tuhan Yang Maha Esa dengan rahmat dan
karunia-Nya penulis dapat menyelesaikan skripsi ini. Skripsi ini disusun sebagai
syarat untuk mendapatkan gelar sarjana pada jurusan Matematika di FMIPA USU.
Dengan kerendahan hati penulis menyadari bahwa skripsi ini masih jauh dari
sempurna, tetapi penulis berharap kiranya skripsi ini dapat menambah bahan bacaan
yang bermanfaat bagi siapa saja yang membacanya. Selama proses penulisan skripsi
ini penulis banyak mendapat bantuan moril maupun materil dari berbagai pihak,
karena itu penulis mengucapkan terimakasih yang sebesar-besarnya kepada :
1. Bapak Drs. Ujian Sinulingga, M.Si dan Drs. Pasukat Sembiring, M.Si, selaku
pembimbing pada penyelesaian skripsi ini yang telah memberi panduan dan
penuh kepercayaan kepada saya untuk menyempurnakan skripsi ini. Panduan
ringkas dan padat serta profesional telah diberikan agar penulis dapat
menyelesaikan tugas ini.
2. Bapak Prof. Dr. Tulus, M.Si selaku ketua dan Sekretaris Departemen
Matematika FMIPA USU.
3. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan
Alam Universitas Sumatera Utara
4. Seluruh dosen pengajar pada Departemen Matematika FMIPA USU yang telah
membagikan ilmunya serta bimbingan dan arahan kepada penulis dan seluruh
staff pegawai yang telah memberikan bantuan dalam penyelesaian skripsi ini.
5. Ayahanda tercinta S. Tarigan Tambun dan Ibunda tercinta M Br Sitepu, kakak
serta adik - adik ku atas segala dukungan yang diberikan baik moril maupun
materil selama penyelesaian skripsi ini.
6. Sahabat-sahabatku yang telah banyak memberi dorongan semangat dan atas
semua bantuannya.
Akhirnya penulis berharap kiranya Tuhan Yang Maha Esa membalasnya kebaikan
dari semua pihak dan kiranya tulisan ini bermanfaat bagi pembaca khususnya bagi
ABSTRAK
Masalah yang dibahas dalam penelitian ini yaitu bagaimana suatu complete
asymmetric digraph sebagai suatu adjacency matriks dapat digunakan untuk
menentukan nilai koefisien korelasi rank kendall ( ). Hasil dari penelitian ini
menunjukkan bahwa suatu complete asymmetric digraph sebagai suatu adjacency
matriks dapat digunakan untuk menentukan koefisien korelasi rank kendall ( ).
USING GRAPH THEORY TO FIND COEFFICIENT CORRELATION RANK KENDALL ( )
ABSTRACT
The problem which is discussed in this research is how to use a complete asymmetric
digraph as a adjacency matrix to find value of coefficient correlation rank kendall ( ).
The result obtained from this research is that a complete asymmetric digraph can be
used to find value of coefficient correlation rank kendall ( ).
DAFTAR ISI
1.2Perumusan Masalah 3
1.3Tinjauan Pustaka 3
1.4Batasan Masalah 4
1.5Tujuan Penelitian 4
1.6Kontribusi Penelitian 4
1.7Metode Penelitian 5
BAB 2 LANDASAN TEORI 6
2.1Pembagian Ilmu Statistik 6
2.2Langkah – langkah Pemilihan Metode Statistik 7
2.3Klasifikasi Data 9
2.4Statistik Nonparametrik 10
2.5Keunggulan Statistik Nonparametrik 11
2.6Keterbatasan Statistik Nonparametrik 12
2.7Korelasi 12
2.7.1 Pengertian Korelasi 12
2.7.2 Koefisien Korelasi 13
2.7.4 Koefisien Rank Korelasi 14
2.7.5 Koefisien Korelasi Rank Kendall ( ) 14
2.7.6 Metode Perhitungan Koefisien Korelasi Rank
Kendall ( ) 14
2.8 Graph Teori 16
2.8.1 Konsep Dasar Graph 16
2.8.2 Graph Tak Berarah (Undirected Graph) 19
2.8.3 Representasi Graph Tidak Berarah (Undirected Graph)
Dalam Matriks 20
2.8.4 Graph berarah (Directed) 23
2.8.4.1 Representasi Graph Berarah (Digraph)
dalam Matriks 24
2.8.4.2 Complete Digraph 25
2.8.4.3 Asymmetric Digraph 25
2.8.4.4 Complete Asymmetric Digraph 26
BAB 3 PEMBAHASAN 27
3.1 Bentuk Graph Sebagai suatu Adjacency Matriks dalam
Menentukan Koefisien Korelasi Rank Kendall ( ) 27
3.2 Penggunaan Model 30
BAB 4 KESIMPULAN DAN SARAN 41
4.1 Kesimpulan 41
4.2 Saran 41
DAFTAR PUSTAKA 42
DAFTAR TABEL
Halaman
Table 3.1 Data Pengamatan Dokter Kepala Bagian Penyakit Dalam
Terhadap 20 Pasien Penderita Darah Tinggi 30
Table 3.2 Ranking Pengamatan Dokter Kepala Bagian Penyakit Dalam
Terhadap 20 Pasien Penderita Darah Tinggi 34
Tabel 3.3 Susunan perankingan Pengamatan Dokter Kepala Bagian
Penyakit Dalam Terhadap 20 Pasien Penderita Darah Tinggi. 35
Tabel 3.4 pasangan yang terurut secara natural (+1) dan pasangan yang
DAFTAR GAMBAR
Halaman
Gambar 2.1 Simple Graph 16
Gambar 2.2 Graph G(6,11) 17
Gambar 2.3 complete graph 19
Gambar 2.4 graph G(5,8) 21
Gambar 2.5 digraph dengan 4 verteks dan 6 arcs 24
Gambar 2.6 complete digraph 25
Gambar 2.7 Asymmetric Digraph 25
Gambar 2.8 Complete Asymmetric Digraph 26
ABSTRAK
Masalah yang dibahas dalam penelitian ini yaitu bagaimana suatu complete
asymmetric digraph sebagai suatu adjacency matriks dapat digunakan untuk
menentukan nilai koefisien korelasi rank kendall ( ). Hasil dari penelitian ini
menunjukkan bahwa suatu complete asymmetric digraph sebagai suatu adjacency
matriks dapat digunakan untuk menentukan koefisien korelasi rank kendall ( ).
USING GRAPH THEORY TO FIND COEFFICIENT CORRELATION RANK KENDALL ( )
ABSTRACT
The problem which is discussed in this research is how to use a complete asymmetric
digraph as a adjacency matrix to find value of coefficient correlation rank kendall ( ).
The result obtained from this research is that a complete asymmetric digraph can be
used to find value of coefficient correlation rank kendall ( ).
BAB 1
PENDAHULUAN
1.1Latar Belakang
Korelasi adalah studi yang membahas tentang derajat hubungan antara dua variabel
atau lebih. Korelasi merupakan salah satu teknik analisis statistika yang banyak
digunakan oleh peneliti karena peneliti umumnya tertarik terhadap peristiwa-peristiwa
yang terjadi dan mencoba menghubungkannya. Besarnya tingkat keeratan hubungan
antara dua variabel atau lebih dapat diketahui dengan mencari besarnya angka korelasi
yang biasa disebut dengan koefisien korelasi.
Metode statistika nonparametrik sering disebut metode bebas sebaran
(distribution free) karena model uji statistiknya tidak menetapkan syarat-syarat
tertentu tentang bentuk-bentuk distribusi parameter populasinya. Uji satistik
nonparametrik hanya menetapkan asumsi/persyaratan bahwa observasi-observasinya
harus independen dan bahwa variabel yang diteliti pada dasarnya harus memiliki
kontinyuitias. Banyak diantara uji-uji statistik nonparametrik kadangkala disebut
sebagai uji ranking, Karena teknik-teknik nonparametrik ini dapat digunakan untuk
skor yang bukan skor eksak dalam pengertian keangkaan, melainkan berupa skor yang
semata-mata berupa jenjang-jenjang (ranks).
Salah satu metode pengukuran koefisien korelasi nonparametrik adalah
koefisien korelasi rank kendall. Koefisien korelasi rank kendall pertama sekali
kendall dinotasikan dengan (tau). Koefisien korelasi rank Kendall ( digunakan
untuk mencari hubungan dan menguji hipotesis antara dua variabel atau lebih, bila
datanya berbentuk ordinal atau ranking.
Derajat keeratan antara dua peubah dapat ditunjukkan oleh rasio
(perbandingan) antara score +1 dan -1 yang sebenarnya (score actual) dengan
maximum score yang dapat dicapai. +1 diberikan untuk pasangan yang tersusun secara
natural dan -1 diberikan untuk pasangan yang tidak tersusun secara natural.
Koefisien korelasi rank kendall ( ) mempunyai kelebihan bila dibandingkan
dengan koefisien korelasi rank spearman (rs). bersifat lebih umum karena dapat
dihitung seperti sebaran normal dan dapat dicari koefisien korelasi parsilnya.
Teori graph pertama kali diperkenalkan oleh Leonard Euler pada tahun 1736
ketika dia membuktikan kemungkinan untuk melewati empat daerah yang terhubung
dengan tujuh jembatan di atas sungai Pregel di Königsberg, Rusia dalam sekali jalan
melewati tiap jembatan tepat sekali saja dan kembali ke tempat semula. Masalah
jembatan Königsberg tersebut dapat dinyatakan dalam bentuk graph dengan
menetukan keempat daerah itu sebagai titik (verteks) dan ketujuh jembatan sebagai
sisi (edge) yang menghubungkan pasangan verteks yang sesuai.
Perhitungan menggunakan graph theory dilakukan dengan membentuk
complete asymmetric digraph dengan vertex adalah setiap objek-objek pada
penelitian. Complete asymmetric digraph kemudian dituangkan ke dalam adjancency
matrix. Dari adjancency matrix yang terbentuk dapat dihitung score actualnya. Dan
untuk score maximum yang dapat dicapai adalah sama dengan jumlah edges dengan n
vertex pada complete asymmetric digraph. Banyaknya arc dapat diperoleh dari .
Sehingga diperoleh koefisien korelasi rank kendall ( ) adalah rasio (perbandingan)
1.2Perumusan Masalah
Yang menjadi permasalahan dalam tulisan ini adalah bagaimana bentuk digraph
sebagai suatu adjacency matrix digunakan pada penentuan koefisien korelasi rank
kendall ( ).
1.3Tinjauan Pustaka
Suatu graph G terdiri dari dua himpunan yang berhingga, yaitu himpunan titik – titik
tidak kosong yang disebut dengan verteks (symbol V(G)) dan himpunan garis – garis
yang disebut dengan edge (simbol E(G)). [6][7]
Suatu graph tak berarah (undirected graph) merupakan kumpulan dari titik
yang disebut dengan verteks dan segmen garis yang menghubungkan dua verteks yang
disebut edge. Secara matematis, sebuah graph G didefenisikan sebagai pasangan
himpunan dimana merupakan himpunan tidak kosong dari verteks – verteks
(simpul atau titik) dan merupakan himpunan tak terurut dari edge (sisi) yang
menghubungkan sepasang verteks. Atau dapat dinotasikan dengan . [2][6]
Suatu graph berarah (digraph) didefenisikan sebagai pasangan himpunan
, dimana merupakan himpunan tidak kosong dari verteks – verteks
(simpul atau titik) dan himpunan terurut yang menghubungkan sepasang verteks
1.4Batasan Masalah
Untuk memperjelas dan memudahkan penelitian ini agar tidak menyimpang dari
sasaran yang dituju maka penulis melakukan pembatasan masalah sebagai berikut:
1. Graph yang digunakan adalah graph berarah (digraph) yang tidak berbobot.
2. Graph sederhana (tidak memuat loop dan arc paralel)
3. Penelitian ini hanya menggunakan jumlah sampel sebanyak 20 sebagai data
simulasi.
1.5Tujuan Penelitian
Tulisan ini diharapkan dapat memperkenalkan model ( cara ) lain untuk menghitung
koefisien korelasi rank kendall . Pada tulisan ini dikenalkan cara menghitung
koefisien korelasi rank kendall menggunakan teori graph.
1.6Kontribusi Penelitian
Hasil dari pemecahan masalah dalam tulisan ini diharapkan dapat memberi manfaat
yaitu mendapatkan cara lain untuk mencari nilai koefisien korelasi rank kendall
1.7Metodologi Penelitian
Langkah-langkah untuk menentukan koefisien korelasi rank kendall ( ) melalui
pendekatan teori graphyaitu:
1. Membentuk complete asymmetric digraph dengan vertex adalah setiap objek
pada penelitian.
2. Membentuk adjacency matrix yang diperoleh dari complete asymmetric
digraph.
3. Menghitung score actual dari adjacency matrix yang terbentuk.
4. Menghitung score maximum yang mungkin. Score maximum sama dengan
jumlah arcs dengan n vertex pada complete asymmetric digraph. Banyaknya
arcs dapat diperoleh dari .
5. Mensubsitusikan score actual dan score maximum yang mungkin ke dalam
rumus koefisien korelasi rank kendall ( ) dengan pendekatan melalui graph
BAB 2
LANDASAN TEORI
2.1 Pembagian Ilmu Statistik
Secara garis besar ilmu statistik dibagi menjadi dua bagian yaitu:
1. Statistik Parametrik
Statistik parametrik adalah ilmu statistik yang digunakan untuk data – data yang
memiliki distribusi normal. Jika data tidak berdistribusi normal maka statistik
nonparametrik dapat digunakan. Apa yang dapat dilakukan jika data tidak
berdistribusi secara normal, namum statistik parametrik tetap ingin digunakan?
Untuk kasus seperti ini data harus ditransformasikan terlebih dahulu. Transformasi
data perlu dilakukan agar data mengikuti distribusi normal. Bagaimana cara
melakukan tranformasi data tidak dibahas dalam tulisan ini.
2. Statistik nonparametrik
Statistik nonparametrik disebut juga statistik bebas distribusi. Statistik
nonparametrik tidak mensyaratkan bentuk distribusi parameter populasi. Statistik
nonparametrik dapat digunakan pada data yang memiliki distribusi normal atau
tidak. Statistik nonparametrik biasanya digunakan untuk melakukan analisis pada
data nominal atau ordinal.
Contoh metode statistik nonparametrik antara lain adalah Median test, Friedman
2.2Langkah – Langkah Pemilihan Metode Statistik
Metode statistik nonparametrik digunakan bila salah satu syarat dalam statistik
parametrik tidak terpenuhi. Syarat – syarat yang perlu diperhatikan untuk menentukan
statistik apa yang digunakan dalam analisis, yaitu:
1. Apakah distribusi data diketahui?
Jika distribusi data tidak diketahui maka statistik yang sesuai adalah statistik
nonparametrik. Jika distribusi data diketahui, maka kita harus melihat jenis
distribusi data tersebut.
2. Apakah data berdistribusi normal?
Jika data tidak berdistribusi normal, maka statistik yang sesuai adalah statistik
nonparametrik. Jika data berdistribusi normal, maka statistik yang sesuai
adalah statistik parametrik.
3. Apakah sampel ditarik secara random?
Jika sampel tidak ditarik secara random maka statistik yang digunakan adalah
statistik nonparametrik. Jika sampel ditarik secara random maka statistik yang
digunakan adalah statistik parametrik.
4. Apakah varians kelompok sama?
Jika varians kelompok tidak sama, maka statistik yang sesuai adalah statistik
nonparametrik. Jika varians kelompok sama, maka statistik yang sesuai adalah
statistik parametrik.
5. Bagaimana jenis skala pengukuran data?
Jika skala pengukuran data nominal dan ordinal, maka statistik yang sesuai
adalah statistik nonparametrik. Jika skala pengukuran data interval dan rasio,
2.3 Klasifikasi Data
Secara umum dapat dikatakan bahwa tujuan diadakannya suatu observasi adalah
memperoleh keterangan tentang bagaimana kondisi suatu objek pada berbagai
keadaan yang ingin diperhatikan. Sebelum melakukan observasi terhadap variabel
yang akan diukur, terlebih dahulu perlu ditentukan skala pengukurannya, karena akan
mempengaruhi metode statistika yang akan digunakan.
Dergibson Siagian dan Sugiarto (2000, Hal: 19) menyatakan bahwa dalam
statistika dibedakan empat macam skala pengukuran yang mungkin dihasilkan yaitu:
1. Skala Nominal
Skala nominal merupakan pengukuran yang paling sederhana. Nominal berasal
dari kata ‘name’. Skala ini mengklasifikasikan (menggolongkan) setiap objek
atau kejadian ke dalam kelompok yang menunjukkan kesamaan atau
perbedaan ciri-ciri objek. Dengan skala nominal,hasil pengukuran bisa
dibedakan tetapi tidak bisa diurutkan mana yang lebih tinggi, mana yang lebih
rendah, mana yang utama dan mana yang bisa dikesampingkan. Setiap
observasi harus dimasukkan pada satu kategori saja tidak boleh lebih. Sebagai
contoh adalah variabel jenis kelamin (pria dan wanita).
2. Skala Ordinal
Dengan menggunakan skala ordinal,objek-objek juga dapat digolongkan dalam
kategori tertentu. Ukuran pada skala ordinal tidak memberika nilai absolute
pada objek, tetapi hanya urutan (ranking) relative saja sehingga kita dapat
mementukan mana yang lebih besar atau kecil (secara umum mana yang lebih
dan mana yang kurang). Sebagai contoh adalah status sosial (rendah, sedang,
3. Skala Interval
Skala interval memberikan ciri angka kepada kelompok objek yang
mempunyai skala nominal dan ordinal, ditambah dengan urutan yang sama
pada urutan objeknya.
Data skala interval diberikan apabila kategori yang digunakan bisa
dibedakan, diurutkan, mempnyai jarak tertentu, tetapi tidak bisa dibandingkan.
Data skala interval diperoleh sebagai hasil pengukuran dan biasanya
mempunyai satuan pengukuran. Cirri penting dari skala interval adalah
datanya bisa ditambahkan, dikurangi, digandakan, dan dibagi tanpa
mempengaruhi jarak relatif skor-skornya. Sebagai contoh, dalam penilaian
kinerja karyawan ( dengan skala 0 – 100 ), A mendapat penilaian 40 dan B
mendapat penilaian 80 bukan berarti kinerja B dua kali kinerja A.
4. Skala Rasio
Skala rasio mempunyai semua sifat skala interval ditambah satu sifat lain,
yaitu memberikan keterangan tentang nilai absolute dari objek yang diukur.
Skala rasio merupakan skala pengukuran yang ditujukan pada hasil
pengukuran yang bisa dibedakan, diurutkan, mempunyai jarak tertentu, dan
bisa dibandingkan. Sebagai contoh adalah umur, nilai uang, tinggi badan, dan
lain sebagainya.
2.4 Statistik Nonparametrik
Istilah nonparametrik pertama kali digunakan oleh Wolfwitz pada tahun 1942. Metode
statistik nonparametrik merupakan metode statistik yang dapat digunakan dengan
mengabaikan asumsi – asumsi yang melandasi penggunaan metode statistik
parametrik terutama yang berkaitan dengan distribusi normal. Istilah lain yang sering
digunakan untuk statistik nonparametrik adalah statistik bebas distribusi (
banyak digunakan pada penelitian – penelitian sosial. Data yang diperoleh pada
penelitian sosial pada umumnya berbentuk kategori atau berbentuk ranking.
Uji statistik nonparametrik adalah suatu uji statistik yang tidak memerlukan
adanya asumsi – asumsi mengenai distribusi data populasi. Uji statistik ini disebut
juga sebagai statistik bebas distribusi (distribution free). Statistik nonparametrik tidak
mensyaratkan bentuk distribusi parameter populasi berdistribusi normal. Statistik
nonparametrik dapat digunakan untuk menganalisis data yang berskala nominal atau
ordinal karena pada umumnya data berjenis nominal dan ordinal tidak berdistribusi
normal. Dari segi jumlah data, pada umumnya statistik nonparametrik digunakan
untuk data berjumlah kecil (n < 30).
2.5 Keunggulan Statistik Nonparametrik
Keunggulan statistik nonparametrik diantaranya:
1. Jika pengujian data menunjukkan bahwa salah satu atau beberapa asumsi yang
mendasari uji statistik parametrik (misalnya mengenai sifat distribusi data)
tidak terpenuhi, maka statistik nonparametrik lebih sesuai diterapkan
dibandingkan statistik parametrik.
2. Uji - ujinya lebih sederhana dan dapat dilaksanakan dengan cepat dan mudah,
sehingga hasil penelitiannya segera dapat disampaikan.
3. Untuk memahami uji – uji dalam statistik nonparametrik tidak memerlukan
dasar matematika serta statistika yang mendalam.
4. Uji – uji pada statistik nonparametrik dapat diterapkan jika kita menghadapi
keterbatasan data yang tersedia, misalnya jika data telah diukur menggunakan
skala pengukuran yang lemah (nominal atau ordinal).
5. Efisiensi statistik nonparametrik lebih tinggi dibandingkan dengan metode
2.6 Keterbatasan Statistik Nonparametrik
Disamping keunggulan, statistik nonparametrik juga memiliki keterbatasan. Beberapa
keterbatasan statistik nonparametrik antara lain:
1. Jika asumsi uji statistik parametrik terpenuhi, penggunaan uji nonparametrik
meskipun lebih cepat dan sederhana akan menyebabkan pemborosan
informasi.
2. Jika jumlah sampel besar, tingkat efisiensi statistik nonparametrik relatif lebih
rendah dibandingkan dengan metode parametrik.
3. Statistik nonparametrik tidak dapat digunakan untuk membuat prediksi
(peramalan).
2.7 Korelasi
2.7.1Pengertian Korelasi
Korelasi adalah statistik yang menyatakan derajat hubungan antara dua variabel atau
lebih tanpa memperlihatkan ada atau tidaknya hubungan kausal di antara variabel –
variabel tersebut.
Dalam korelasi akan dijumpai bahwa dua variabel bernilai positif, negatif
dan/atau nol. Dua variabel dikatakan berkorelasi positif jika kenaikan pada satu
variabel diikuti oleh kenaikan variabel lainnya dan/atau penurunan pada satu variabel
diikuti oleh penurunan variabel lainnya. Dengan kata lain dua variabel berkorelasi
positif jika variabel – variabelnya cenderung berubah secara bersama. Dua variabel
dikatakan berkorelasi negatif jika kenaikan pada satu variabel diikuti oleh penurunan
cenderung berubah dalam arah yang berlawan. Dua variabel dikatakan berkorelasi nol
jika perubahan satu variabel tidak ada hubungannya dengan variabel lainnya. Dengan
kata lain dua variabel dikatakan tidak berkorelasi.
2.7.2 Koefisien Korelasi
Besarnya tingkat keeratan hubungan antara dua variabel dapat diketahui dengan
mencari besarnya angka korelasi yang disebut koefisien korelasi. Koefisien korelasi
dinyatakan dengan lambang . Jika yang diukur adalah korelasi antara variabel x
dengan variabel y dinotasikan dengan .
Nilai dari koefisien korelasi berada diantara -1 dan +1. Jika dua variabel
berkorelasi positif maka nilai koefisien korelasi akan mendekati +1, jika dua variabel
berkorelasi negative maka nilai koefisien korelasi akan mendekati -1, jika dua variabel
tidak berkorelasi maka nilai koefisien korelasi akan bernilai 0. Sehingga besarnya nilai
koefisien korelasi dapat ditulis dalam pertidaksamaan .
2.7.3 Koefisien Determinasi
Koefisien determinasi merupakan pangkat dua dari koefisien korelasi, dinotasikan
dengan . Koefisien determinasi yaitu koefisien yang menunjukkan/menentukan
berapa besar peranan variabel x dalam menentukan besarnya y.
Apabila suatu variabel x mempunyai korelasi dengan variabel y dengan
determinasinya adalah yang menyatakan besarnya persentase x
menjelaskan y.
2.7.4 Koefisien Rank Korelasi
Untuk data ; i = 1, 2, 3, …, n yang berskala ordinal maka koefisien korelasi
antara x dan y dihitung berdasarkan statistika nonparametrik yang disebut dengan
koefisien rank korelasi. Koefisien rank korelasi pada statistika nonparametrik antara
lain koefisien rank korelasi Spearman, Kendall, Somer, Crammer dan sebagainya.
2.7.5 Koefisien Korelasi Rank Kendall
Koefisien korelasi rank kendall mempunyai kegunaan untuk mengukur derajat
hubungan dari dua peubah yang pengukurannya minimal dalam skala ordinal. Metode
ini dikemukakan untuk pertama kalinya oleh Maurice G. Kendall pada tahun 1938.
Koefisien korelasi rank kendall dinotasikan dengan .
2.7.6 Metode Perhitungan Koefisien Korelasi Rank Kendall ( )
Koefisien korelasi rank kendall ( ) dapat diperoleh dengan cara membandingkan score
actual dengan score maximum yang mungkin dicapai. Atau dengan kata lain score
actual adalah score +1 dan -1 yang sebenarnya. +1 diberikan untuk pasangan yang
tersusun secara natural dan -1 diberikan untuk pasangan yang tidak tersusun secara
yang dapat diuraikan menjadi . Sehingga koefisien korelasi rank
Kendall ( ) dapat dirumuskan :
Selanjutnya score actual diberi symbol S, dan score maksimum ditentukan
oleh susunan , dimana n adalah jumlah objek atau individu pada variabel random X
dan Y. Secara matematis dapat ditulis:
Atau
Dimana : S = score actual (jumlah score +1 dan -1)
n = jumlah objek atau individu pada variabel random X dan Y
Ada kalanya pada variabel random X dan Y mempunyai objek yang sama atau
sering disebut dengan rank kembar. Jika ada dua atau lebih nilai pengamatan (baik
untuk variabel random X atau Y) yang sama, maka nilai – nilai tersebut diberi rank
rata – rata. Pengaruh dari nilai rank kembar tersebut adalah merubah besarnyanilai
penyebut pada rumus koefisien korelasi rank kendall ( ). Dalam hal ini rumus
Dimana : S = score actual (jumlah score +1 dan -1)
n = jumlah objek atau individu pada variabel random X dan Y
= ; t adalah jumlah rank kembaran tiap kelompok
kembarnya untuk variabel X
= ; t adalah jumlah rank kembaran tiap kelompok
kembarannya untuk variabel Y
2.8 Graph Theory
2.8.1 Konsep Dasar Graph
Defenisi 2.1 Graph
Suatu graph G terdiri dari dua himpunan yang berhingga, yaitu himpunan titik – titik
tidak kosong yang disebut dengan verteks yang disimbolkan dengan V(G) dan
himpunan garis – garis yang disebut dengan edge yang disimbolkan dengan E(G).
Defenisi 2.2 Loop, Edge Paralel dan Simpel Graph
Sebuah edge yang menghubungkan pasangan verteks yang sama yakni disebut
loop. Dua edge yang berbeda yang menghubungkan verteks yang sama disebut edge
paralel. Dan jika ada suatu graph yang tidak memuat loop dan edge paralel disebut
simple graph (graph sederhana).
V1 e6 V4
e1 e2 e3 e4
V2 e5 V3
Defenisi 2.3 incident dan adjacent
Suatu edge dalam suatu graph G dengan verteks – verteks ujung dan disebut
saling insiden dengan dan sedangkan dan disebut dua buah verteks yang
saling adjacent. Dua buah edge dan disebut saling adjacent jika kedua edge
tersebut incident pada suatu verteks persekutuan. Sebagai contoh dapat dilihat pada
gambar 2.2.
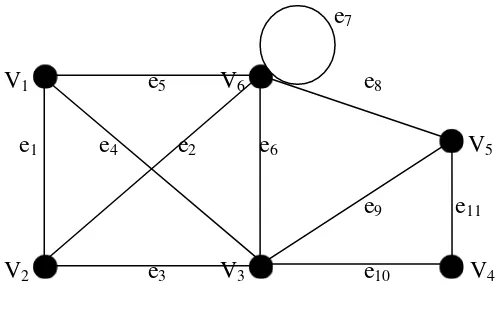
Gambar 2.2 Graph G(6,11)
Dari graph diatas dapat dilihat bahwa dan adalah lima buah edge
yang incident dengan verteks . Sedangkan dan merupakan dua buah edge
yang adjacent dan dengan adalah dua buah verteks yang adjacent.
Defenisi 2.3 Degree
Degree dari sebuah verteks dalam graph G adalah jumlah edge yang incident
dengan , dengan loop dihitung dua kali. Degree dari sebuah verteks dinotasikan
dengan . Bila jumlah edge yang incident dengan jumlah verteks adalah n
maka degree dari adalah n dan dinotasikan dengan .
Sebagai contoh, pada gambar 2.2dapat dilihat bahwa = = 3, = 5 ,
= = 2, dan = 6
Jika pada suatu graph ada suatu verteks yang tidak incident dengan suatu edge
atau dengan kata lain degree dari verteks tersebut sama dengan nol. Verteks itu
Defenisi 2.4 Graph Lengkap (Complete Graph)
Graph lengkap (complete graph) dengan n verteks (disimbolkan dengan ) adalah
graph sederhana dengan n verteks, dimana setiap 2 verteks bebeda dihubungkan
dengan suatu edge.
Teorema 2.4.1
Banyaknya edge dalam suatu graph lengkap dengan n verteks adalah atau
buah.
Bukti
Misalkan G adalah suatu graph lengkap dengan n verteks . Ambil
sembarang verteks (sebutlah ). Karena G merupakan graph lengkap, maka
dihubungkan dengan verteks lainnya ). Jadi ada buah
edge.
Selanjutnya, ambil sembarang verteks kedua (sebutlah ). Karena G adalah graph
lengkap, maka juga dihubungkan dengan semua verteks sisanya
sehingga ada buah edge yang berhubungan dengan . Salah satu edge
tersebut dihubungkan dengan . Garis ini sudah diperhitungkan pada waktu
menghitung banyaknya edge yang berhubungan dengan . Jadi ada edge
yang belum diperhitungkan.
Proses dilanjutkan dengan menghitung banyaknya edge yang berhubungan dengan
dan yang belum diperhitungkan sebelumnya. Banyak edge yang
didapat berturut – turut adalah : , , …, 3, 2, 1.
Jadi secara keseluruhan terdapat
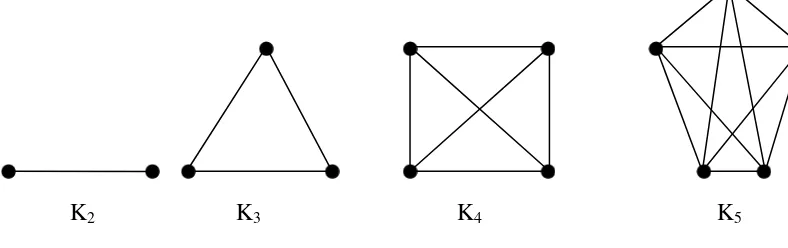
Sebagai contoh dapat dilihat gambar 2.3 dibawah ini:
K2 K3 K4 K5
Gambar 2.3 complete graph
2.8.2 Graph Tak Berarah ( undirected Graph )
Suatu graph tak berarah (undirected graph) merupakan kumpulan dari titik yang
disebut verteks dan segmen garis yang menghubungkan dua verteks yang disebut
edge. Secara matematis, sebuah graph G didefenisikan sebagai pasangan himpunan
( ).
Dimana: = himpunan tak kosong dari verteks – verteks (simpul atau titik)
=
= himpunan tak terurut dari edge (sisi) yang menghubungkan sepasang
verteks.
Atau dapat dinotasikan dengan
Defenisi diatas menyatakan bahwa dimana V tidak boleh kosong,
sedangkan E mungkin kosong sehingga sebuah graph dimungkinkan tidak mempunyai
2.8.3 Representasi Graph Tidak Berarah (Undirected graph) dalam Matriks
Matriks dapat digunakan untuk menyatakan suatu graph. Untuk menyelesaikan suatu
permasalahan model graph dengan bantuan komputer maka graph tersebut dapat
disajikan dalam bentuk matriks. Matriks – matriks yang dapat menyajikan model
graph tersebut antara lain:
1. Matriks Ruas
Matriks ruas adalah matriks yang berukuran atau yang
menyatakan ruas (edge) dari graph. Matriks ini tidak dapat mendeteksi adanya
verteks terpencil.
2. Matriks adjacency
Matriks adjacency merupakan matriks simetri. Matriks adjacency digunakan
untuk menyatakan graph dengan cara menyatakannya dalam jumlah edge yang
menghubungkan verteks – verteksnya. Jumlah baris dan kolom matriks
adjacency sama dengan jumlah verteks dalam graph. Sehingga matriks
hubungnya berbentuk matriks bujur sangkar.
Defenisi matriks adjacency:
Misalkan G adalah graph tak berarah dengan verteks (n
berhingga). Matriks hubung yang sesuai dengan graph G adalah matriks
dengan = jumlah edge yang menghubungkan verteks dengan
verteks ; .
Karena jumlah edge yang menghungkan verteks dengan verteks selalu
sama dengan jumlah edge yang menghubungkan dengan verteks maka
jelas bahwa matriks adjacency selalu merupakan matriks yang simetris
Notasi dari matiks adjacency yaitu:
1 jika ada edge dari verteks ke verteks
=
3. Matriks Incidence
Matriks incidence adalah matriks yang menghubungkan verteks dengan edge.
Notasi dari matriks incidence yaitu:
1 jika verteks terhubung ke edge
= 2 jika edge menghubungkan verteks ke verteks
0 dalam hal lain
4. Matriks Connection
Matriks connection dapat mendeteksi suatu graph terhubung atau tidak. Graph
terhubung jika dan hanya jika matriks tidak mengandung elemen nol. Tetapi
matriks connection tidak ada mendeteksi adanya edge sejajar dan loop.
Notasi dari matriks connection yaitu:
1 bila atau ada edge dari verteks ke verteks
=
0 Dalam hal lain
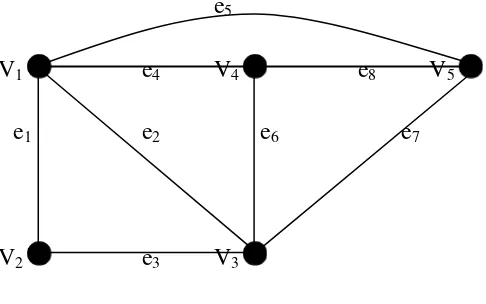
Sebagai contoh untuk graph seperti dibawah ini:
e5
V1 e4 V4 e8 V5
e1 e2 e6 e7
V2 e3 V3
Maka,
Matriks ruas:
Atau
Matriks adjacency:
Matriks Incidence:
Matriks connection:
2.8.4 Graph Berarah ( Directed Graph )
Suatu graph berarah (digraph) D adalah merupakan suatu pasangan dari himpunan
{V(D), A(D)} dimana V(D) = adalah himpunan berhingga yang tidak
kosong yang elemennya disebut node/vertex dan A(D) = adalah suatu
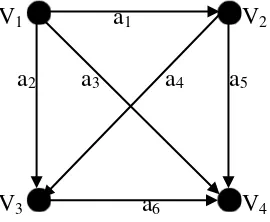
Suatu vertex didalam digraph D disajikan dengan sebuah titik dan sebuah arc
yang digambarkan berupa suatu penggalan garis dengan suatu anak panah dari vertex
ke vertex . Sebagai contoh, gambar dibawah ini menampilkan suatu digraph yang
terdiri dari empat verteks dan enam arcs.
V1
2.8.4.1Representasi Graph Berarah (Digraph) dalam Matriks
Cara menyatakan graph berarah dalam matris sebenarnya tidaklah jauh berbeda
dengan cara menyatakan graph tak berarah dalam suatu matriks. Perbedaannya hanya
terletak pada keikutsertaan informasi tentang arah garis yang terdapat dalam graph
berarah. Sebuah graph berarah dapat juga dipersentasekan dalam matriks adjacency,
matriks incidence dan matriks sirkuit. Adapun reorentase matriks dalam graph berarah
yang dibahas dalam tulisan ini adalah matriks adjacency.
Defenisi dari Matriks Adjacency tersebut adalah sebagai berikut:
Misalkan G adalah graph berarah yang terdiri dari n verteks tanpa arc paralel. Matriks
hubung yang sesuai dengan graph G adalah matriks bujursangkar
dengan notasi
1 jika ada arc dari verteks ke verteks
=
2.8.4.2Complete Digraph
Digraph disebut sebagai complete digraph (graf berarah lengkap) jika setiap pasang
vertex dihubungkan oleh sebuah arc. Atau sebuah graph adalah komplit jika setiap
vertex terhubung ke setiap vertex yang lain. Pada gambar di bawah ini dapat dilihat
suatu complete digraph.
Gambar 2.6 complete digraph
2.8.4.3Asymmetric Digraph
Suatu digraph dikatakan sebagai asymmetric digraph jika pada digraph yang terbentuk
memiliki paling banyak satu arc antara sepasang vertex tanpa loop. Dengan kata lain
tidak ada arc yang memiliki arc balik. Pada gambar dibawah ini dapat dilihat suatu
asymmetric digraph.
2.8.4.4Complete Asymmetric Digraph
Complete asymmetric digraph adalah suatu asymmetric digraph dimana terdapat tepat
satu antara setiap pasang vertex. Complete asymmetric digraph dengan vertices
mengandung arcs.
Bukti
Misalkan D adalah suatu complete asymmetric digraph dengan n verteks
. Ambil sembarang verteks (sebutlah ). Karena D merupakan
complete asymmetric digraph, maka dihubungkan dengan verteks lainnya
). Jadi ada buah arc.
Selanjutnya, ambil sembarang verteks kedua (sebutlah ). Karena D adalah complete
asymmetric digraph, maka juga dihubungkan dengan semua verteks sisanya
sehingga ada buah arc yang berhubungan dengan . Proses
dilanjutkan dengan menghitung banyaknya arc yang berhubungan dengan
dan yang belum diperhitungkan sebelumnya. Banyak arc yang
didapat berturut – turut adalah : , , …, 3, 2, 1.
Jadi secara keseluruhan terdapat
buah arc
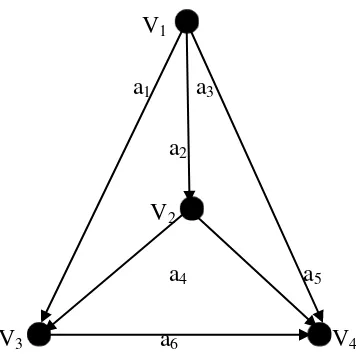
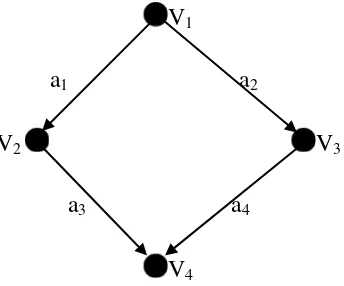
Pada gambar dibawah ini dapat dilihat suatu contoh dari complete asymmetric
digraph.
V1 a1 V2
a2 a3 a4 a5
V3 a6 V4
Complete asymmetric digraph dapat direpresentasikan dalam sebuah matriks
adjacency. Jumlah baris dan kolom adjacency matrix sama dengan jumlah vertex
dalam complete asymmetric digraph. Adjacency matrix yang sesuai adalah matrix
bujur sangkar , yaitu matriks A = dengan:
+1 jika ada arc dari titik ke dan ( ) tersusun secara natural
= -1 jika ada arc dari titik ke dan ( ) tidak tersusun secara natural
BAB 3
PEMBAHASAN
3.1 Bentuk Graph Sebagai Suatu Adjacency Matriks dalam Penentuan Koefisien Korelasi Rank Kendall ( )
Graph yang digunakan dalam penentuan koefisien korelasi rank kendall ( ) adalah
graph yang berarah (digraph), karena setiap objek pengamatan pada data yang
diberikan merupakan data berpasangan berurutan. Vertexnya adalah objek-objek
dalam penelitian. Dalam metode korelasi rank Kendall, objek-objek pengamatan
dihubungkan kesetiap objek-objek berikutnya yaitu dari objek pertama ke objek
kedua, kemudian dari objek pertama ke objek ke tiga, dan seterusnya sampai objek
ke-n. Setelah itu dilanjutkan dari objek kedua ke objek ketiga, objek kedua ke objek
keempat, dan seterusnya sampai objek n. Hal ini terus dilakukan sampai objek
ke-(n-1) ke objek ke-n. Atau dengan kata lain, jika objek-objek pada penelitian adalah
vertex dalam graph maka dari pengertian di atas dapat dituliskan:
(vi,vj) dengan i < j ; i,j = 1,2,3,…,n.
vi merupakan titik awal dan vj merupakan titik akhir, sehingga suatu arc dengan titik
ujung (vi,vj) menyatakan garis dari titik i dan titik j. Karena (vi,vj) dihubungkan hanya
sekali dengan i < j ; i,j = 1,2,3,…,n sehingga tidak ada garis paralel dan tidak ada arc
dengan titik ujung (vi,vi) maka graph yang terbetuk adalah suatu asymetric digraph.
Dan karena setiap pasang objek pada penelitian harus dihubungkan atau dengan kata
lain terdapat tepat satu arc antara setiap pasang vertex (vi,vj) dengan i < j ; i,j =
1,2,3,…,n maka bentuk graph yang digunakan dalam perhitungan adalah suatu
complete asymmetric digraph.
Complete asymmetric digraph yang terbentuk kemudian dituangkan ke dalam
vertex dalam complete asymmetric digraph. Adjacency matrix yang sesuai adalah
matrix bujur sangkar , yaitu matriks A = dengan:
+1 jika ada arc dari verteks ke dan ( ) tersusun secara natural
= -1 jika ada arc dari verteks ke dan ( ) tidak tersusun secara natural
1 jika tidak ada arc dari verteks ke
Sehingga terbentuk adjacency matrix-nya menjadi:
A=
Setelah adjacency matrix terbentuk dengan ketentuan seperti diatas,
selanjutnya ditentukan score actual dengan cara menjumlahkan nilai +1 dan -1 yang
diperoleh dari adjacency matrix. Kemudian menentukan score maximum yang
mungkin dicapai. Score maximum yang mungkin sama dengan banyaknya arcs dari
complete asymmetric digraph, sehingga score maximum dapat ditentukan dengan
dimana n adalah jumlah vertex dari complete asymmetric digraph.
Dengan demikian koefisien korelasi rank kendall ( dengan pendekatan
Atau
Untuk koefisien korelasi rank kendall dengan rank kembar maka rumus yang
digunakan adalah :
Dengan: S = score actual
; t adalah jumlah rank kembaran tiap kelompok kembarnya
untuk peubah x
; t adalah jumlah rank kembaran tiap kelompok kembarnya
untuk peubah y
Selanjutnya kita dapat menyusun hipotesis nihil dan hipotesis alternative yang
nantinya dapat diuji dengan uji hipotesis menggunakan rumusan:
Dimana : Z = test statistik untuk kendall rank korelasi
= koefisien korelasi rank kendall
3.2 Penggunaan Model
Sebagai uji model perhitungan koefisien korelasi rank Kendall ( ) menggunakan
graph theory, dicontohkan data berikut ini yang hanya merupakan data simulasi. Data
simulasi diambil dari buku statistik nonparametrik edisi kedua karangan Samsubar
Saleh. Berikut ini adalah data pengamatan dokter kepala bagian penyakit dalam
terhadap 20 pasien penderita darah tinggi.
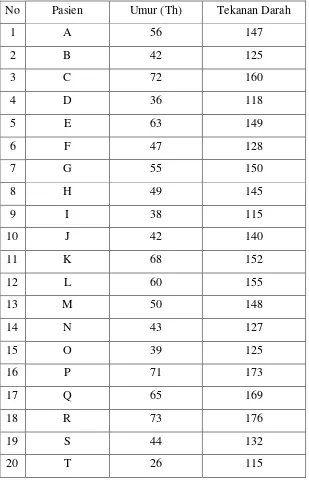
Table 3.1 Data Pengamatan Dokter Kepala Bagian Penyakit Dalam Terhadap 20
Pasien Penderita Darah Tinggi
Untuk mendapatkan nilai skor maksimum dari data diatas maka dapat diperoleh dari
jumlah arc maksimum yang diperoleh dari complete asymmetric digraph. 20 pasien
penderita darah tinggi menjadi verteks dari complete asymmetric digraph. Score
maximum sama dengan banyaknya arcs dari complete asymmetric digraph, sehingga
score maximum dapat ditentukan dengan dimana n adalah jumlah vertex dari
complete asymmetric digraph. Dari data diatas diketahui banyaknya n adalah 20,
sehingga score maksimum dapat diperoleh dari banyaknya arc dari complete
asymmetric digraph dengan menggunakan teorema 2.4.1, maka nilai score maksimum
dapat diperoleh dengan:
=
Dapat direpresentasikan dengan digraph akan diperoleh graph dengan 20 verteks dan
190 arcs. Dan dapat dilihat dalam gambar berikut :
V1 V2
V3 V4 V5
V6 V7 V8 V9
V10 V11 V12 V13 V14
V15 V16 V17 V18 V19 V20
Sehingga skor maksimum yang diperoleh adalah sama dengan banyaknya arc dari
complete asymmetric digraph yaitu 190.
Untuk menentukan nilai skore actualnya dapat diperoleh dengan menggunakan
matriks adjacency yang berbentuk matriks segitiga atas. Langkah – langkah untuk
mendapatkan matriks adjacency adalah sebagai berikut:
Lakukan perangkingan dari data diatas, dan akan diperoleh urutan ranking sebagai
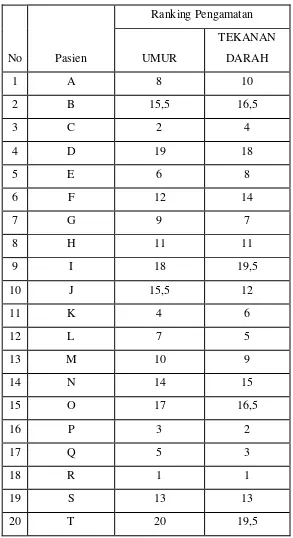
Table 3.2 Ranking Pengamatan Dokter Kepala Bagian Penyakit Dalam Terhadap
20 Pasien Penderita Darah Tinggi
Selanjutnya perankingan tersebut susun berdasarkan urutannya. Hasilnya disajikan
dalam tabel berikut ini:
Tabel 3.3 Susunan perankingan Pengamatan Dokter Kepala Bagian Penyakit
Dalam Terhadap 20 Pasien Penderita Darah Tinggi.
Setelah rank umur diurutkan secara natural, langkah selanjutnya adalah membentuk
Dari adjacency matriks diatas dihitung total nilai +1 dan -1. Dari sini diperoleh score
actual. Besarnya score actual dapat dilihat dari table dibawah ini. Setiap baris dalam
table ini menunjukkan banyaknya nilai +1 (pasangan yang tersusun secara natural)
dan banyaknya nilai -1 (pasangan yang tidak tersusun secara natural) dari setiap baris
dalam adjacency matriks.
Tabel 3.4 pasangan yang terurut secara natural (+1) dan pasangan yang tidak tersusun
secara natural (-1) dari setiap baris dalam adjacency matriks
Banyak Pasangan Yang terurut secara
natural (+1)
Banyak pasangan yang tidak terurut
Dari table diatas diperoleh score actual dengan menjumlahkan banyak pasangan yang
terurut secara natural dengan banyak pasangan yang tidak tersusun secara natural.
Karena yang akan diuji memiliki rank kembar, maka selanjutnya dicari nilai Tx dan
Ty. Dimana pengamatan terhadap umur dimisalkan dengan x dan pengamatan
terhadap tekanan darah dimisalkan dengan y. Pada rank pengamatan terhadap umur
terdapat satu kelompok nilai kembar yaitu: ranking 15,5 dengan t = 2. Sehingga nilai
Tx adalah :
=
= 1
Pada rank pengamatan terhadap tekanan darah terdapat dua kelompok nilai kembar
yaitu: ranking 16,5 dengan t = 2 dan ranking 19,5 dengan t = 2. Sehingga nilai Ty
adalah :
=
Dengan demikian harga koefisien korelasi rank Kendall dapat dicari
menggunakan rumus (3.3):
Selanjutnya pengujian terhadap :
1. Menentukan hipotesis nihil dan hipotesis alternative, yaitu:
H0 : tidak ada korelasi antara umur dengan tekanan darah
H1 : ada korelasi antara umur dengan tekanan darah
2. Kriteria pengambilan keputusan:
H0 diterima dan H1 ditolak apabila - Zα/2 ZH ≤ + Zα/2
H0 ditolak dan H1 diterima apabila ZH > + Zα/2 atau ZH < - Zα/2
4. Nilai kritis pada = 5% = ± Z1/2(1 ) = Z1/2(1-0,05)
Z1/2(0,95) = Z0,475 = ± 1,96 (gunakan kurva normal)
5. Kesimpulan
H0 ditolak karena ZH = 5,2330 > Z0,025 = + 1,96
Artinya : ada korelasi yang cukup berarti antara umur dengan tekanan darah dari 20
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
1. untuk menentukan score maksimum dapat diperoleh dari jumlah arc dari complete
asymmetric digraph.
2. Untuk mendapatkan score actual dapat diperoleh dengan menggunakan matriks
adjacency dari complete asymmetric digraph yang berbentuk matriks segitiga atas.
3. Dari hasil pembahasan diatas dapat disimpulkan bahwa graph berarah (digraph)
dapat digunakan untuk menentukan nilai koefisien korelasi rank kendall ( ).
4.2 Saran
Adapun saran yang dapat penulis berikan adalah:
1. Diharapkan untuk dapat membuat suatu program komputerisasi untuk mencari
koefisien korelasi rank kendall menggunakan graph teori mengingat akan ada data
yang berskala besar. Dengan adanya program komputerisasinya bentuk graph dari
adjacency matriksnya juga dapat tersaji dengan jelas, sehingga pembaca bisa
DAFTAR PUSTAKA
[1] Alavi, Y, Dkk. 1985. Graph Theory with Applications to Algorithms and
Computer Science. USA: John Wiley & Sons, Inc
[2] Beineke, Lowell W & Wilson, Robin J. 1983. Selected Topics in Graph Theory 2.
New York: Academic Press Inc.
[3] Djarwanto Ps. Edisi 2004. Statistika Nonparametrik. Yogyakarta:
BPFE-Yogyakarta
[4] Harary, Frank. 1971. Graph Theory. Second Printing. Philippines:
Addison-Wesley Publishing Company, Inc.
[5
[6] Johnsonbaugh, R. 2002. Matematika Diskrit. Jilid 2. Edisi Bahasa Indonesia.
Terjemahan Pearson Education Asia Pte.ltd. dan PT. Prenhallindo.
[7] Munir, Rinaldi. 2007. Matematika Diskrit. Edisi Ketiga. Bandung: Informatika
[8] Narsingh, Deo. 1984. Graph Theory with application to Engineering and
Computer Science. New Delhi: Prentice Hall of India, Private Limited.
[9] Palmer, Edgar M. 1985. Graphical Evolution. Amsterdam: Mathematisch
Centrum.
[10] Siagian,dkk. 2000. Metode statistika untuk bisnis dan ekonomi. Jakarta: PT
Gramedia Pustaka Utama
[11] Saleh, Samsubar. 1996. Statistik Nonparametrik. Edisi Kedua. Yogyakarta:
BPFE-Yogyakarta
[12] Wilson, Robin J. 1985. Introduction to Graph Theory. Third Edition. New York: