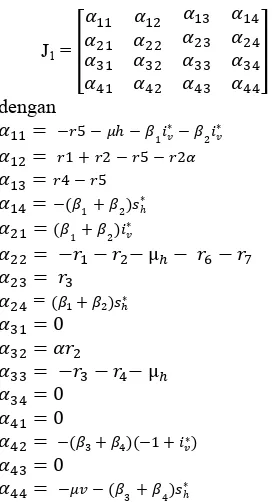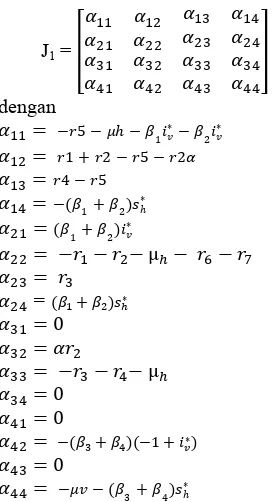ABSTRACT
SUGANDI PUTRA GINTING. Dynamic population of human and the vector in the infectious malaria disease through Plasmodium falciparum and Plasmodium vivax parasites. Supervised by PAIAN SIANTURI and ALI KUSNANTO.
Malaria is a disease that transmitted to human by the bitting of infectious Anopheles mosquitoes. This infectious desease caused by parasite genus Plasmodium. There are two species of the parasites studied here, that cause human malaria namely Plasmodium vivax and Plasmodium falciparum. The mathematical model in discribing the transmission of Plasmodium falciparum and Plasmodium vivax on human population is divided into four classes, the susceptible, the infectious, the dormant, and the recovered classes.
Mosquitoes that caused malaria are called the vector. In this case, the vector population is divided into two classes, the susceptible and infectious classes. There are two equilibrium states, a disease free state E0 and an endemic state E1. The stability of E0 and E1 is determined by considering the basic reproductive number (R0). The E0 is stable if R0 is less than one. On the other hand, the point E1 was stable given the value of R0 is greater than one.
ABSTRAK
SUGANDI PUTRA GINTING. Dinamika populasi manusia dan vektor pada penularan penyakit malaria oleh Plasmodium falciparum dan Plasmodium vivax. Dibimbing oleh PAIAN SIANTURI dan ALI KUSNANTO.
Malaria adalah penyakit yang ditularkan kepada manusia melalui gigitan nyamuk Anopheles. Malaria merupakan penyakit menular yang disebabkan oleh parasit genus Plasmodium. Terdapat dua jenis parasit yang menyebabkan penyakit malaria dalam studi ini, yaitu Plasmodium vivax dan Plasmodium falciparum. Model matematik untuk menggambarkan transmisi antara Plasmodium falciparum dan Plasmodium vivax dalam populasi manusia dibagi menjadi empat kelas yaitu kelas rentan, kelas tertular, kelas dorman, dan kelas pulih.
Nyamuk penyebab malaria ini selanjutnya disebut vektor. Pada kasus ini akan dibedakan populasi vektor menjadi dua kelas yakni, kelas yang rentan terhadap infeksi dan kelas yang telah terinfeksi. Terdapat dua titik kesetimbangan tetap yaitu titik bebas penyakit (E0) dan titik endemik (E1). Kestabilan E0 dan E1 ditentukan oleh bilangan reproduksi dasar (R0). Titik E0 adalah stabil ketika R0 < 1. Sebaliknya jika R0 > 1, titik E1 adalah stabil.
I PENDAHULUAN
1.1 Latar Belakang
Malaria telah diketahui sejak dahulu kala dan demam dikenal sebagai tanda orang yang akan terjangkit penyakit ini. Hal ini ditulis dalam sejarah tulisan Mesir kuno yang mengemukakan bahwa penyakit malaria disebabkan oleh parasit dari genus Plasmodium
yang dapat ditemukan pada burung, mamalia dan kadal, dimana proses penularannya melalui gigitan nyamuk Anopheles. Protozoa parasit jenis ini banyak sekali tersebar di wilayah tropik, misalnya di Amerika, Asia dan Afrika. Terdapat empat jenis parasit malaria yaitu,
Plasmodium vivax, Plasmodium falciparum,
Plasmodium ovale, dan Plasmodium malariae
dan lebih dari 3 ratus juta kasus malaria per tahun dengan 1 sampai 1,5 juta kasus kematian setiap tahunnya (kebanyakan terjadi pada anak-anak).
Dalam karya ilmiah ini akan dibahas suatu model SIDRS (Susceptible Infected Dormant
Removed Susceptible) dari penularan penyakit
malaria dalam suatu populasi. Terdapat 247 juta kasus malaria di dunia dan lebih dari satu juta kasus kematian setiap tahunnya (WHO, 2010). Pada kasus ini akan dibahas mengenai penyebaran penyakit malaria di Thailand. Malaria di Thailand ditemukan di sepanjang perbatasan Burma, Kamboja, dan Malaysia. Infeksi yang timbul dari Plasmodium
falciparum, Plasmodium vivax dan Plasmodium
malariae masing-masing berkembang menjadi
50-60%, 40-50% dan kurang dari 1%. Sedangkan Plasmodium ovale tidak ditemukan di Thailand. Di antara ketiga masalah malaria di atas yang menjadi permasalahan yang sangat besar ditemukan pada kasus Plasmodium vivax.
Pada tahun 1994 ditemukan 109.321 kasus malaria dan 45.123 di antaranya merupakan kasus malaria yang diakibatkan oleh
Plasmodium vivax.
Parasit malaria memiliki siklus kehidupan ganda yang sangat rumit, yaitu siklus reproduksi seksual terjadi pada tubuh nyamuk sendiri sedangkan reproduksi aseksualnya terjadi pada manusia. Pada reproduksi aseksual, terdapat
tahapan yang disebut tahap berenang bebas yakni tahap sporozoite. Parasit malaria dalam tahap ini akan diinfeksikan ke dalam aliran darah manusia melalui kulit manusia oleh nyamuk. Sporozoite ini akhirnya memasuki sel darah merah manusia, dimana bentuk awalnya ialah seperti cincin dan seperti bentuk amuba sebelum terjadi tahap pembelahan yang akan menjadi bentuk yang lebih kecil yang disebut
merozoite. Sel darah merah yang mengandung
merozoite ini kemudian akan pecah dan
melepaskan merozoite tersebut ke dalam aliran darah. Pada tahap ini penderita akan menggigil dan demam yang merupakan ciri khas dari penyakit malaria. Merozoite-merozoite ini akan menginfeksi sel-sel darah merah yang lain dan membangun siklus yang berulang.
Lebih dari dua milyar orang atau total 41% dari populasi dunia tinggal di daerah dimana malaria ditularkan secara teratur (misalnya, bagia Afrika, Timur Tengah, Amerika Selatan, Hispania dan Oseania) dan ada sekitar 1,5-2,7 juta orang yang meninggal akibat malaria setiap tahun. Perkembangan Plasmodium vivax
berbeda dengan Plasmodium falciparum yakni seseorang yang menderita Plasmodium
falciparum akan sembuh dari kesehatan yang
paling buruk (jika tidak meninggal), namun seorang yang terinfeksi Plasmodium vivax tidak akan meninggal namun akan tetap menderita kambuh.
1.2 Tujuan
Tujuan penulisan karya ilmiah ini adalah :
1. Mempelajari model matematika dari sistem penularan penyakit malaria dalam suatu populasi.
2. Menganalisis titik tetap yang diperoleh. 3. Melakukan simulasi terhadap model
yang diberikan sehingga terlihat parameter yang mempengaruhi populasi.
II LANDASAN TEORI
2.1 Persamaan Diferensial Linear Orde 1 Suatu persamaan yang dinyatakan sebagai
g , .
disebut persamaan diferensial (PD) linear orde 1. Jika g(t) = 0, PD disebut PD homogen dan jika g(t) ≠ 0, PD disebut PD linear tak homogen.
(Tu 1994)
2.2 Sistem Persamaan Diferensial Mandiri Suatu persamaan diferensial (SPD) dinyatakan sebagai
, . dengan f fungsi kontinu bernilai real dari x dan mempunyai turunan parsial kontinu. SPD tersebut disebut SPD mandiri (autonomous) bilamana tidak memuat waktu (t) secara eksplisit di dalamnya. tetap disebut juga titik kritis atau titik keseimbangan. Untuk selanjutnya akan digunakan istilah titik tetap.
(Tu 1994)
2.4 Nilai Eigen dan Vektor Eigen
Diberikan matriks koefisien konstan A berukuran n x n, dengan SPD homogen berikut , = , (2.3) Suatu vektor tak nol x dalam ruang
disebut vektor eigen dari A jika untuk suatu
skalar berlaku
Ax = λx (2.4) Nilai skalar dinamakan nilai eigen dari A. Untuk mencari nilai dari matriks A, maka persamaan (4) dapat ditulis kembali sebagai ( A- I )x = 0 (2.5) dengan I matriks identitas. Persamaan (2.5) mempunyai solusi tak nol jika dan hanya jika
p( ) = det( A- λI ) = │A- I│= 0 (2.6) Persamaan (6) disebut persamaan karakteristik dari matriks A. sehingga didapat persamaan linear
2.6 Kestabilan Titik tetap Diberikan SPD sebarang
, . (2.8)
Tentukan titik tetap yang memenuhi
f . Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigennya, yaitu :λidimana i = 1,2,…,n yang diperoleh dari
persamaan karakteristik (2.5).
Secara umum kestabilan titik tetap mempunyai tiga perilaku :
2. Tak Stabil, jika terdapat paling
sedikit satu i dimana Re(λi ) > 0.
3. Sadel, jika perkalian dua buah nilai eigen sembarang adalah negatif (λiλj <
0 untuk i dan j sembarang).
(Tu 1994)
2.7 Kondisi Routh Hurwitz
Misalkan a1, a2,…, ak bilangan-bilangan real, aj
= 0 jika j > k. Semua nilai eigen dari persamaan karakteristik
p(λ) = λk +a1λk-1 +…+ ak-2 λ2 + ak-1 λ1 + ak = 0
mempunyai bagian real yang negatif jika dan hanya jika determinan dari matriks i x i, untuk
Sehingga menurut kondisi Routh-Hurwitz, untuk suatu k, k = 2, 3, 4 disebutkan bahwa titik tetap
Hurwitz disajikan pada teorema 1 dan 2 berikut.
Teorema 1
Misalkan A, B, C bilangan real. Bagian real dari setiap nilai eigen persamaan karakteristik
p( λ) = λ3 +A λ2 + Bλ + C = 0 (2.9) adalah negatif jika dan hanya jika A > 0, C > 0 dan AB > C.
Teorema 2
Misalkan A,B,C dan D bilangan real. Bagian real dari setiap nilai eigen persamaan karakteristik
Bilangan Reproduksi Dasar ditulis R0 adalah
nilai harapan dari kasus kedua yang dihasilkan pada suatu populasi yang seluruhnya rentan oleh suatu jenis individu yang terinfeksi/menular. Kondisi yang timbul adalah :
1. Jika R0 < 1, maka setiap individu yang menular akan menginfeksi kurang dari satu individu baru dan penyakit tidak akan berkembang.
2. Jika R0 > 1, maka setiap individu yang menular akan menginfeksi lebih dari satu individu baru, dan penyakit tersebut dapat menyerang populasi sehingga menjadi wabah.
3.1 Perumusan Model
Model yang akan dibahas dalam karya ilmiah ini adalah model SIDRS (Susceptible
Infected Dormant Removed Susceptible) dari
penularan penyakit malaria dalam suatu populasi. Dalam model ini terdapat tiga populasi yang berbeda yaitu rentan S(t), terinfeksi I(t), dan sembuh R(t).S(t) digunakan untuk mewakili jumlah orang yang belum terinfeksi oleh penyakit pada waktu t, atau mereka yang rentan terhadap penyakit. I(t) menunjukkan jumlah individu yang telah terinfeksi oleh penyakit dan mampu menyebarkan penyakit kepada mereka yang masuk dalam kategori rentan. R(t) digunakan untuk menunjukkan banyaknya orang-orang yang telah terinfeksi dan kemudian pulih dari penyakit.
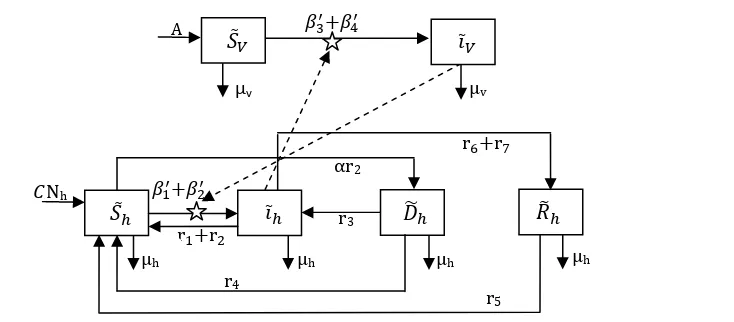
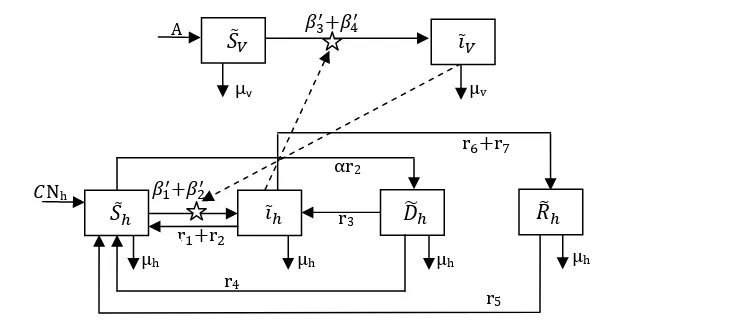
Secara skematik, diagram alur model SIDRS pada penularan penyakit malaria dalam suatu populasi ditunjukkan pada diagram kompartemen di bawah (Gambar 1). Misalkan jumlah populasi pada waktu t dinyatakan dengan N = Nh(t). Populasi ini dibagi menjadi
digolongkan ke kelas rentan ( ) dengan laju
kelahiran sebesar C. Individu yang berada di kelas rentan akan mengalami kematian dengan laju kematian sebesar , atau masuk ke kelas terinfeksi ( ) karena terjangkit plasmodium
falciparum ( ′) dan plasmodium vivax ( ′).
Laju penularan individu dari kelas rentan ( ) ke kelas Dorman ( ) karena terjangkit
plasmodium vivax namun tidak terlihat gejala
sebesar . Selanjutnya individu yang berada di kelas terinfeksi akan mati dengan laju kematian sebesar , atau sembuh dan masuk ke kelas rentan karena tidak adanya sistem kekebalan tubuh dengan laju atau sembuh dengan laju penyembuhan sebesar sehingga dimasukkan ke kelas sembuh ( ). Kemudian individu di kelas sembuh akan mati dengan laju kematian sebesar , atau menjadi rentan kembali karena sistem kekebalan tubuh dapat hilang sehingga kembali masuk ke kelas rentan dengan laju hilangnya kekebalan tubuh sebesar . Individu yang berada pada kelas Dorman ( ) akan mengalami kematian dengan laju atau sewaktu-waktu dapat kehilangan kekebalan tubuh dan masuk ke kelas terinfeksi dengan laju r3 atau sembuh namun
kehilangan kekebalan tubuh dengan laju r4 dan
menjadi rentan kembali sehingga siap untuk terinfeksi.
Selain itu, pada diagram kompartemen di atas (Gambar 1) terdapat diagram alur yang
menjelaskan populasi vektor yang membawa virus malaria. Diagram ini akan menunjukkan 2 Gambar 1 Diagram model penularan penyakit malaria pada manusia (yang dibagi dalam empat
kelas , ̃ , , dan ) dan populasi vektor (yang dibagi dalam dua kelas dan ̃ )
̃
kelas yang berbeda yakni kelas rentan S = (t) yakni ditujukan kepada populasi vektor yang masih steril dari virus malaria dan kelas infeksi
I = (t) yaitu ditujukan kepada vektor yang sudah terinfeksi oleh virus malaria. Total populasi vektor dinyatakan dengan NV = +
. Vektor yang lahir digolongkan ke dalam populasi rentan ( ) dengan laju kelahiran A. Vektor yang berada di kelas rentan akan mengalami kematian dengan laju μv , atau masuk ke kelas terinfeksi ( ) dengan laju
.
Selanjutnya vektor yang berada pada kelas terinfeksi akan mengalami kematian dengan laju μv. Laju perubahan populasi manusia atau vektor pada suatu kelas ialah jumlah manusia atau vektor yang masuk dalam kelas tersebut dikurangi dengan jumlah manusia atau vektor yang meninggalkan kelas tersebut. Penjelasan di atas dapat dituliskan dalam bentuk persamaan-persamaan berikut:
µh adalah laju kematian populasi
µv adalah laju kematian vektor
adalah laju penularan P.falciparum dari nyamuk ke tubuh manusia
adalah laju penularan P.vivax dari nyamuk ke tubuh manusia
adalah laju penularan P.falciparum dari tubuh manusia ke tubuh nyamuk
adalah laju penularan P.vivax dari tubuh manusia ke tubuh nyamuk
adalah laju kelahiran populasi
Nh adalah total banyaknya populasi
α adalah rasio dorman manusia yang terinfeksi
adalah tingkat dimana seseorang terinfeksi P.falciparum
adalah tingkat dimana seseorang terinfeksi P.vivax
adalah tingkat dimana manusia tidak aktif namun akan kambuh kembali adalah laju pemulihan manusia yang dorman oleh P.vivax
adalah tingkat pemulihan manusia dan akan menjadi manusia yang rentan adalah laju pemulihan manusia dari infeksi P.falciparum
adalah laju pemulihan manusia dari infeksi P.vivax
(t) adalah banyaknya vektor rentan (t) adalah banyaknya vektor menular
dengan kondisi sh+ih+dh+rh=1 dan sv+iv=1, dan ,
,
Selanjutnya akan dicari titik tetap untuk persamaan (3.7), (3.8), (3.9), dan (3.10) yang kemudian akan dianalisis kestabilan di sekitar titik tetap tersebut serta dinamika populasinya.
3.2 Titik Tetap
Analisis titik tetap pada SPD sering digunakan untuk menentukan suatu solusi konstan. Titik tetap dari persamaan .
. akan diperoleh dengan menetapkan
sh(t) = 0, ih(t)= 0, dh(t) = 0 dan
iv(t) sehingga diperoleh
persamaan-persamaan di bawah ini:
(i) persamaan di atas secara serentak akan diperoleh dua titik tetap yaitu titik tetap tanpa penyakit dan titik tetap endemik.
3.3 Titik Tetap tanpa Penyakit
Titik tetap tanpa penyakit merupakan kondisi dimana semua individu sehat dan tetap sehat tiap waktu dengan kata lain tidak terdapat penyakit. Titik tetap ini diperoleh ketika banyaknya vektor yang terinfeksi sama dengan nol ( ) yang didapat dari persamaan (iv), kemudian disubstitusi ke persamaan (i), (ii), dan (iii) maka akan diperoleh nilai , , dan sehingga diperoleh titik tetap dari persamaan-persamaan (3.7), (3.8), (3.9), dan (3.10) yaitu , , , .
3.4 Titik Tetap Endemik
Pada titik tetap endemik akan menghasilkan solusi nontrivial. Di sini titik tetap endemik merupakan kondisi dimana penyakit masih terdapat di dalam populasi
vektor dan manusia. Dari persamaan (19), (20), (21), dan (22) diperoleh titik tetap endemik
E1 = (sh*,ih*,dh*,iv*) dengan
3.5. Analisis Kestabilan Titik Tetap
Misalkan persamaan (3.7)-(3.10) dituliskan sebagai berikut :
sh(t) = A(sh, ih, dh, iv)
ih(t) = B(sh, ih, dh, iv)
dh(t)= C(sh, ih, dh, iv)
iv(t)= D(sh, ih, dh, iv)
Dari persamaan di atas dapat diperoleh matriks
Jacobi.
J0 =
=
dengan,
J = { } untuk I = 1, 2, 3, 4 dan j =1, 2, 3, 4
3.5.1 Kestabilan Titik Tetap tanpa Penyakit Pelinearan pada titik tetap akan menghasilkan matriks Jacobi sebagai berikut:
Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik
det J . Persamaan
karakteristik dari J adalah ( +µ + ) ( t t t ) = 0 sehingga diperoleh salah satu nilai eigen dari J yaitu = µ r dan nilai eigen yang lainnya diperoleh dari akar polinomial
Karena semua parameter yang terlibat positif maka t , , dan t
sehingga kestabilan di titik bergantung pada nilai . Kondisi akan terpenuhi ketika R0 < 1 maka titik tetap stabil dan sebaliknya kondisi tidak dipenuhi ketika
R0> 1 maka titik tetap sadel. Kondisi stabil
yang dipenuhi ketika R0 < 1 dimana R0 merupakan bilangan reproduksi dasar virus dalam populasi , sehingga ketika
merupakan kondisi stabil asimtotik karena virus malaria tidak dapat bertahan dalam populasi. Sebaliknya, ketika merupakan kondisi tidak stabil karena virus malaria dapat bertahan dan meningkat dalam populasi. Sehingga menurut kriteria Routh-Hurwitz, titik E0 stabil.
3.5.2 Kestabilan Titik Tetap Endemik
Pelinearan pada titik tetap akan menghasilkan matriks Jacobi sebagai berikut:
J1 =
Untuk memperoleh nilai eigen digunakan persamaan karakteristik det J . Persamaan karakteristik dari J adalah
w w w w dan nilai
eigennya diperoleh dari akar polinomial p( λ) = λ4
+w3 λ3 + w2 λ2 + w1λ + w0 = 0. Karena
semua parameter yang terlibat positif maka
w , , dan dengan
menggunakan software Mathematica dibuktikan
w sehingga menurut
Routh-Hurwitz, titik stabil.
Berikut ini adalah tabel kondisi kestabilan dari kedua titik tetap yang diperoleh.
Tabel 1 Kondisi kestabilan titik tetap.
Kondisi
Simpul stabil
Spiral Tidak stabil
Sadel Spiral stabil
Dari Tabel 1 dapat dilihat bahwa kondisi kestabilan dari titik tetap yang diperoleh saling bertentangan. Ketika titik tetap yang pertama stabil, titik tetap yang kedua tidak stabil dan ketika titik tetap yang pertama tidak stabil, titik tetap yang kedua stabil.
0 200 400 600 800 1000 1200 1400 0.0 3.6 Dinamika Populasi Penularan Malaria
Untuk mengamati pengaruh masuknya virus malaria ke dalam populasi manusia maupun vektor pada waktu tertentu maka diperlukan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi dengan variabel waktu. Hal ini membutuhkan nilai awal untuk semua parameter dan variabel.
Pada proses penggambarannya diambil nilai awal populasi nyamuk atau vektor yang terinfeksi adalah 5% dari total populasi nyamuk.
Dalam karya ilmiah ini dianalisis dinamika populasi untuk dua kondisi yaitu
di mana populasi akan stabil karena penyakit hilang dari populasi dan di mana penyakit bertahan dalam populasi dan meningkat menjadi wabah.
3.6.1 Dinamika Populasi untuk
Proses penggambarannya dengan menggunakan Mathematica 7 yang dievaluasi ketika ditetapkan h = 0.0000421 per hari yang sesuai dengan harapan hidup yang sesungguhnya dari 65 tahun untuk manusia, dan
V = 1/30, yang sesuai dengan harapan hidup dari 30 hari untuk nyamuk Anopheles. Nilai-nilai = 1/20 per hari dan = 1/14 per hari, sesuai dengan waktu yang dibutuhkan orang manusia yang terinfeksi dengan P. falciparum
dan P.vivax untuk meninggalkan kelas
terinfeksi dan menjadi rentan kembali, yaitu 20 hari untuk P. falciparum dan 14 hari untuk P .
vivax. Nilai-nilai = 1/365 per hari, =
1/(2*365) per hari sesuai dengan waktu yang dibutuhkan orang yang terinfeksi P.vivax untuk meninggalkan kelas dorman, yaitu 1 tahun untuk memasuki kelas yang terinfeksi , dan 2 tahun untuk memasuki kelas rentan. Nilai =1/(3*365) per hari sesuai dengan 3 tahun bagi orang-orang yang terinfeksi dengan P.vivax
akan kehilangan sistem imun. Nilai-nilai = 1 / 30 per hari, = 1 / 25 per hari sesuai dengan waktu yang dibutuhkan orang-orang yang terinfeksi P.falciparum dan P.vivax untuk pulih, yakni 30 hari untuk P.falciparum dan 25 hari untuk P.vivax, α = 0.65. Untuk mendapatkan titik tetap pada keadaan bebas penyakit yang stabil lokal, kita menetapkan masing-masing , , , sama dengan 0.025, 0.024, 0.03 dan 0.02.
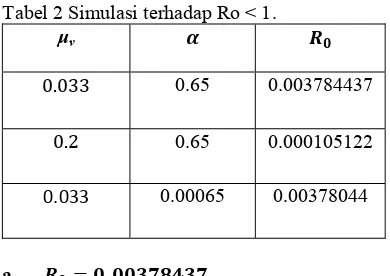
Untuk nilai dilakukan analisis untuk tiga kondisi yang berbeda dengan
mengubah nilai (laju kematian vektor) dan α (rasio dorman manusia yang terinfeksi) seperti yang ditunjukkan pada tabel berikut.
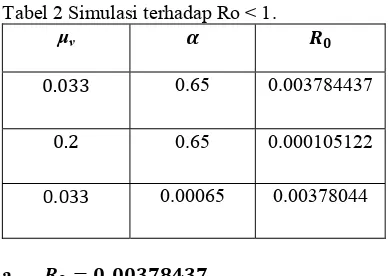
Tabel 2 Simulasi terhadap Ro < 1. μv
. 0.65 0.003784437
. 0.65 0.000105122
0.033 0.00065 0.00378044
a. .
Kondisi . dipenuhi
ketika = 0.033 dan α = 0.65. Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,
Gambar 2 Dinamika populasi , . , dan terhadap waktu t.
Pada gambar di bawah ini akan dilakukan simulasi populasi Sh terhadap waktu t dengan
0 200 400 600 800 1000 1200 1400
0.0
0 200 400 600 800 1000 1200 1400 0.0
ketika rasio jumlah manusia yang terinfeksi virus tetap dengan α = 0.65 dan laju kematian murni pada vektor dinaikkan menjadi . sehingga diperoleh gambar dinamika populasi di bawah ini,
Gambar 4 Dinamika populasi , . , dan terhadap waktu t.
Pada gambar di bawah ini akan dilakukan simulasi populasi Sh terhadap waktu t dengan
mengubah nilai parameter dan .
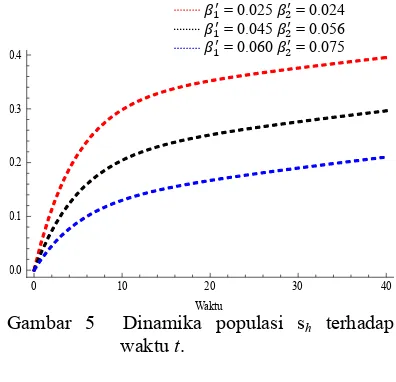
Gambar 5 Dinamika populasi sh terhadap
waktu t.
c. .
Kondisi . dipenuhi ketika rasio jumlah manusia yang terinfeksi virus diturunkan menjadi α = 0.00065 dan laju kematian murni pada vektor tetap . sehingga diperoleh gambar dinamika populasi di bawah ini,
Gambar 6 Dinamika populasi , . , dan terhadap waktu t.
Pada Gambar 2, Gambar 4 dan Gambar 6 dapat dilihat bahwa kurva Sh stabil naik menuju
satu, namun pada kurva Ih stabil turun menuju
ke nol. Hal ini berarti bahwa banyaknya manusia yang terinfeksi akan mengurangi banyaknya manusia yang rentan karena total populasi dianggap konstan. Penurunan pada kurva mengakibatkan penurunan pada kurva
Ih, hal ini dikarenakan semakin sedikit jumlah
nyamuk yang terinfeksi sehingga jumlah manusia yang terinfeksi pun semakin sedikit. Pada kurva Dh dapat kita lihat awalnya
mengalami sedikit kenaikan dan kemudian stabil turun menuju kepunahan. Hal ini berarti semakin sedikit jumlah nyamuk yang terinfeksi sehingga jumlah manusia yang dorman pun semakin sedikit. Pada Gambar 2, Gambar 4 dan Gambar 6 dilakukan simulasi dengan mengubah nilai parameter dan . Jika nilai
semakin besar maka jumlah manusia yang rentan akan semakin besar dan jika nilai
semakin kecil maka akan terjadi penurunan pada jumlah manusia rentan. Jika nilai semakin besar maka jumlah manusia rentan akan semakin kecil.
Gambar 3 dan Gambar 5 menunjukkan hubungan populasi Sh terhadap waktu t. Ketiga
kurva di atas dibandingkan berdasarkan nilai ′ dan ′ yang berbeda yaitu ′ = 0.025 dan
′ = 0.024, ′ = 0.045 dan ′ = 0.056, ′ =
0.060 dan ′ = 0.075. Dari kurva di atas dapat dilihat bahwa manusia yang rentan mengalami terus penaikan yang tajam menuju satu yang artinya menuju kestabilan. Semakin besar nilai
′ dan ′, kurva akan mengalami penaikan
ketika laju penularan Plasmodium falciparum
dan Plasmodium vivax dari nyamuk ke tubuh
manusia meningkat ′ dan ′ mengakibatkan banyaknya manusia yang rentan menurun.
3.6.2 Dinamika Populasi untuk
Proses penggambarannya dengan menggunakan Mathematica 7 yang dievaluasi ketika ditetapkan h = 0.0000421 per hari yang sesuai dengan harapan hidup yang sesungguhnya dari 65 tahun untuk manusia, dan
V = 1/120, yang sesuai dengan harapan hidup dari 30 hari untuk nyamuk Anopheles. Nilai-nilai = 1/20 per hari dan = 1/14 per hari, sesuai dengan waktu yang dibutuhkan orang manusia yang terinfeksi dengan P. falciparum
dan P.vivax untuk meninggalkan kelas
terinfeksi dan menjadi rentan kembali, yaitu 20 hari untuk P. falciparum dan 14 hari untuk P .
vivax. Nilai-nilai = 1/365 per hari, =
1/(2*365) per hari sesuai dengan waktu yang dibutuhkan orang yang terinfeksi P.vivax untuk meninggalkan kelas dorman, yaitu 1 tahun untuk memasuki kelas yang terinfeksi , dan 2 tahun untuk memasuki kelas rentan. Nilai =1/(3*365) per hari sesuai dengan 3 tahun bagi orang-orang yang terinfeksi dengan P.vivax
akan kehilangan sistem imun. Nilai-nilai = 1 / 30 per hari, = 1 / 25 per hari sesuai dengan waktu yang dibutuhkan orang-orang yang terinfeksi P.falciparum dan P.vivax untuk pulih, yakni 30 hari untuk P.falciparum dan 25 hari untuk P.vivax, α = 0.70. Untuk mendapatkan titik tetap pada keadaan endemik yang stabil lokal, kita menetapkan masing-masing , , , sama dengan 0.14, 0.1, 0.15 dan 0.1.
Untuk nilai dilakukan analisis untuk tiga kondisi yang berbeda dengan mengubah nilai (laju kematian vektor) dan α (rasio dorman manusia yang terinfeksi) seperti yang ditunjukkan pada tabel berikut.
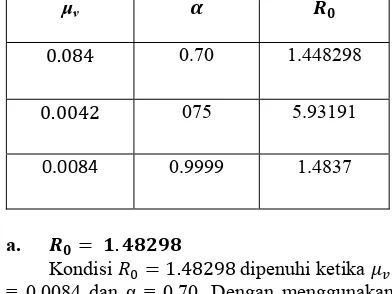
Tabel 3 Simulasi terhadap Ro >1.
μv
. 0.70 1.448298
. 075 5.93191
0.0084 0.9999 1.4837
a. .
Kondisi . dipenuhi ketika = 0.0084 dan α = 0.70. Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,
Gambar 7 Dinamika populasi , . , dan terhadap waktu t.
Pada gambar di bawah ini akan dilakukan simulasi populasi Sh terhadap waktu t dengan
mengubah nilai parameter dan .
Gambar 8 Dinamika populasi sh terhadap
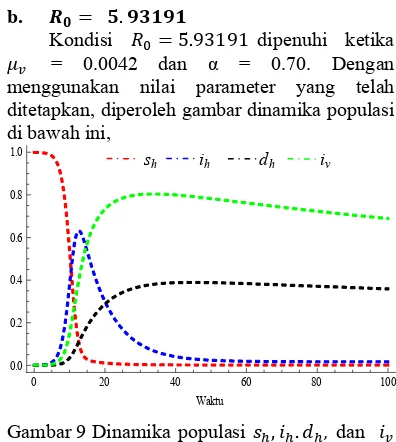
menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,
Gambar 9 Dinamika populasi , . , dan terhadap waktu t.
Pada gambar di bawah ini akan dilakukan simulasi populasi Sh terhadap waktu t dengan
mengubah nilai parameter dan .
Gambar 10 Dinamika populasi sh terhadap
waktu t.
c. .
Kondisi . dipenuhi ketika = 0.0084 dan α = 0.9999. Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,
Gambar 11 Dinamika populasi , . , dan terhadap waktu t.
Gambar 7, Gambar 9 dan Gambar 11 menunjukkan hubungan antara Sh, Ih, Dh, dan
terhadap waktu t. Kurva Sh terus menurun
menjauhi satu dan kurva Ih dan Dh naik
menjauhi nol serta kurva terus naik mendekati satu dan turun kembali namun bertahan pada titik kesetimbangannya, ini menunjukkan bahwa kurva Sh, Ih, Dh, dan
menjauhi , , , yang menandakan bahwa titik tetap tanpa penyakit tidak stabil pada sedangkan titik tetap endemik menjadi stabil di mana keempat kurva dapat dilihat menuju kestabilan titik tetap . Ini menunjukkan kondisi ketika penyakit dapat bertahan pada populasi.
Gambar 8 dan Gambar 10 merupakan dinamika populasi Sh terhadap waktu t. Ketiga
kurva tersebut dibandingkan berdasarkan nilai nilai ′ dan ′ yang berbeda yaitu ′
. dan ′ . , ′ . dan ′ 0,22,
. dan ′ . Semakin besar nilai , kurva terlihat semakin signifikan ke bawah sebelum kemudian menuju kestabilan . Laju manusia yang rentan ketika
′ . dan ′ . lebih kecil dari laju
manusia rentan ketika ′ . dan ′ . dan laju manusia rentan ketika . dan
′ . lebih kecil dari laju manusia rentan
ketika ′ . dan ′ . dan ′ . dan ′ . . Ini berarti bahwa semakin besar laju penularan Plasmodium falciparum
dan Plasmodium vivax dari nyamuk ke tubuh
manusia dan maka laju manusia yang rentan semakin kecil.
0 200 400 600 800 1000 1200 1400 0.0 5% dari total populasi nyamuk .
maka populasi manusia yang rentan adalah 100% dari total populasi manusia , sehingga kondisi awal lainnya dan
. Ketika populasi awal nyamuk yang terinfeksi 50% dari total populasi nyamuk
. maka populasi manusia yang rentan adalah 100% dari total populasi manusia
sehingga kondisi awal yang lainnya
dan .
Berikut akan dibandingkan dinamika populasi dan pengaruhnya terhadap populasi manusia ketika populasi awal vektor yang terinfeksi 5% dan 50% dari total populasi vektor untuk R0 < 1 dan R0 > 1.
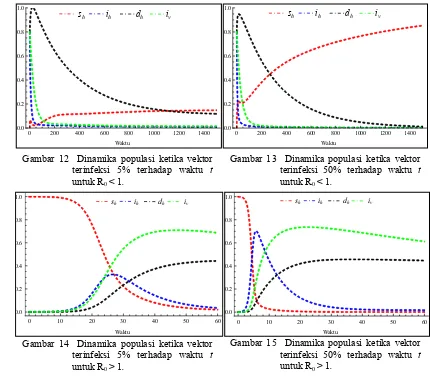
Pada Gambar 12 dan Gambar 13 dapat dilihat bahwa kurva nyamuk yang terinfeksi 5% lebih curam dibandingkan 50%. Hal ini dikarenakan nyamuk yang terinfeksi 50% lebih banyak menginfeksi manusia dibandingkan 5%. Sehingga pada kurva infeksi 50% garis kurva manusia rentan lebih datar dibanding pada kurva infeksi 5% yang cenderung lebih tajam kenaikannya. Dengan kata lain banyaknya nyamuk yang terinfeksi mempengaruhi jumlah manusia yang terinfeksi atau tertular. Semakin
banyak nyamuk yang terinfeksi semakin banyak pula manusia yang terinfeksi.
Berbeda halnya pada Gambar 14 dan Gambar 15 dapat dilihat bahwa kurva nyamuk yang terinfeksi 50% lebih curam dibandingkan 5%. Peningkatan banyaknya manusia yang terinfeksi lebih cepat terjadi pada nyamuk yang terinfeksi 50%. Hal ini dikarenakan nyamuk yang terinfeksi 50% lebih banyak menginfeksi manusia dibandingkan 5%.
0 200 400 600 800 1000 1200 1400 0.0
Gambar 12 Dinamika populasi ketika vektor terinfeksi 5% terhadap waktu t
untuk R0 < 1.
Gambar 13 Dinamika populasi ketika vektor terinfeksi 50% terhadap waktu t
untuk R0 < 1.
Gambar 14 Dinamika populasi ketika vektor terinfeksi 5% terhadap waktu t
untuk R0 > 1.
Gambar 15 Dinamika populasi ketika vektor terinfeksi 50% terhadap waktu t
untuk R0 > 1.
IV SIMPULAN
Dalam tulisan ini telah dipelajari model matematika dari penularan penyakit malaria untuk Plasmodium falciparum dan Plasmodium
vivax . Dari model tersebut dihasilkan dua titik
tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik.
Terdapat dua titik kesetimbangan tetap yaitu titik bebas penyakit (E0) dan titik endemik (E1). Kestabilan E0 dan E1 ditentukan oleh rumusan yang disebut bilangan reproduksi dasar (R0). Titik E0 adalah stabil ketika R0 kurang dari satu. Sebaliknya jika R0 lebih besar dari satu, titik E1 adalah stabil.
Dari grafik bidang solusi dapat dilihat bahwa ketika nilai laju penularan virus dari tubuh nyamuk ke tubuh manusia diperbesar mengakibatkan laju manusia rentan semakin kecil. Semakin banyak nyamuk yang terinfeksi semakin sedikit manusia yang rentan. Ketika laju kematian nyamuk semakin besar maka jumlah populasi manusia rentan akan semakin besar, demikian sebaliknya jika laju kematian
nyamuk semakin kecil maka populasi manusia rentan akan semakin kecil.
Banyaknya populasi awal nyamuk yang terkena virus sangat berpengaruh ke dalam populasi manusia, khususnya manusia rentan. Semakin banyak populasi awal nyamuk yang terkena virus maka populasi manusia rentan akan semakin cepat berkurang, demikian sebaliknya.
Dalam karya tulis ini, dinamika populasi manusia dan vektor digambarkan dalam beberapa contoh ilustratif dengan banyaknya vektor yang terinfeksi sebesar 5% dan 50%. Diperoleh hasil bahwa untuk , populasi vektor yang dengan terinfeksi 5% mencapai kestabilan lebih cepat daripada populasi vektor dengan terinfeksi 50%. Untuk
, terjadi situasi yang berkebalikan. Dalam penelitian ini juga ditunjukkan bahwa interaksi antara manusia yang rentan dengan manusia terinfeksi tidak berpengaruh terhadap dinamika populasi manusia.
DINAMIKA POPULASI MANUSIA DAN VEKTOR PADA PENULARAN PENYAKIT MALARIA
OLEH PLASMODIUM FALCIPARUM DAN PLASMODIUM VIVAX
SUGANDI PUTRA GINTING
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
DAFTAR PUSTAKA
Anton, H. 1995. Aljabar Linear Elementer
(Edisi ke-5). Terjemahan Pantur Silaban
dan I Nyoman Susila. Erlangga, Jakarta. Driessche, PVD dan Watmough, J. 2005.
Reproduction Number and Sub-Threshold Endemic Equilibria for Compartemental
Model of Disease Transmission. Math.
Biosci : 1-21
Pongsumpan P dan Tang I.M. Mathematical Model of Plasmodium Vivax and
Plasmodium Falciparum Malaria. Applied
Mathematical Sciences, Vol. 3, (2009), pp. 283–290.
Strogatz, SH. 1994. Nonlinear Dynamics and Chaos, With Applications to Physics,
Biology, Chemistry, and Engineering.
Addison-Wesley Publishing Company, Reading, Massachusete.
TU PNV. 1994. Dynamical System, An Introduction with Application in
Economics and Biology. Springer-Verlag.
Heidelberg, Germany.
WHO. 2010. Malaria. http://www.who.int/
mediacentre/ diakses pada tanggal 31
Januari 2010.
DINAMIKA POPULASI MANUSIA DAN VEKTOR PADA PENULARAN PENYAKIT MALARIA
OLEH PLASMODIUM FALCIPARUM DAN PLASMODIUM VIVAX
SUGANDI PUTRA GINTING
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
ABSTRACT
SUGANDI PUTRA GINTING. Dynamic population of human and the vector in the infectious malaria disease through Plasmodium falciparum and Plasmodium vivax parasites. Supervised by PAIAN SIANTURI and ALI KUSNANTO.
Malaria is a disease that transmitted to human by the bitting of infectious Anopheles mosquitoes. This infectious desease caused by parasite genus Plasmodium. There are two species of the parasites studied here, that cause human malaria namely Plasmodium vivax and Plasmodium falciparum. The mathematical model in discribing the transmission of Plasmodium falciparum and Plasmodium vivax on human population is divided into four classes, the susceptible, the infectious, the dormant, and the recovered classes.
Mosquitoes that caused malaria are called the vector. In this case, the vector population is divided into two classes, the susceptible and infectious classes. There are two equilibrium states, a disease free state E0 and an endemic state E1. The stability of E0 and E1 is determined by considering the basic reproductive number (R0). The E0 is stable if R0 is less than one. On the other hand, the point E1 was stable given the value of R0 is greater than one.
ABSTRAK
SUGANDI PUTRA GINTING. Dinamika populasi manusia dan vektor pada penularan penyakit malaria oleh Plasmodium falciparum dan Plasmodium vivax. Dibimbing oleh PAIAN SIANTURI dan ALI KUSNANTO.
Malaria adalah penyakit yang ditularkan kepada manusia melalui gigitan nyamuk Anopheles. Malaria merupakan penyakit menular yang disebabkan oleh parasit genus Plasmodium. Terdapat dua jenis parasit yang menyebabkan penyakit malaria dalam studi ini, yaitu Plasmodium vivax dan Plasmodium falciparum. Model matematik untuk menggambarkan transmisi antara Plasmodium falciparum dan Plasmodium vivax dalam populasi manusia dibagi menjadi empat kelas yaitu kelas rentan, kelas tertular, kelas dorman, dan kelas pulih.
Nyamuk penyebab malaria ini selanjutnya disebut vektor. Pada kasus ini akan dibedakan populasi vektor menjadi dua kelas yakni, kelas yang rentan terhadap infeksi dan kelas yang telah terinfeksi. Terdapat dua titik kesetimbangan tetap yaitu titik bebas penyakit (E0) dan titik endemik (E1). Kestabilan E0 dan E1 ditentukan oleh bilangan reproduksi dasar (R0). Titik E0 adalah stabil ketika R0 < 1. Sebaliknya jika R0 > 1, titik E1 adalah stabil.
DINAMIKA POPULASI MANUSIA DAN VEKTOR PADA PENULARAN PENYAKIT MALARIA
OLEH PLASMODIUM FALCIPARUM DAN PLASMODIUM VIVAX
SUGANDI PUTRA GINTING
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul : Dinamika populasi manusia dan vektor pada penularan penyakit
malaria oleh Plasmodium falciparum dan Plasmodium vivax
Nama : Sugandi Putra Ginting NRP : G54063323
Menyetujui
Pembimbing I Pembimbing II
Dr. Paian Sianturi Drs. Ali Kusnanto, M.Si
NIP. 19620212 199011 1 001 NIP. 19650820 198903 1 001
Mengetahui
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS NIP. 19650505 198903 2 004
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Tuhan Yesus atas segala berkat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini juga tidak terlepas dari dukungan dan bantuan berbagai pihak. Penulis mengucapkan terimakasih yang sebesar-besarnya kepada:
1. Keluargaku terkasih: Bapak dan mamak terkasih, yang telah memberikan kasih sayang, doa, didikan, serta dukungan baik secara moril dan materi, nasihat, dan motivasi yang sangat berharga bagi penulis. “Kekelengenndu la erleka man bangku”. Untuk kakak dan abangku, Kak Tua, Kak Susi, Bang Jefry terimakasih selalu memberikan semangat dan nasihat bagi penulis;
2. Dr. Paian Sianturi. selaku dosen pembimbing I, Drs. Ali Kusnanto, M.Si. selaku pembimbing II. Terimakasih atas waktu, ilmu yang diberikan dan kesabarannya dalam membimbing penulis. Semua ilmu yang Pak Paian dan Pak Ali berikan sangat bermanfaat bagi penulis. TERIMA KASIH;
3. Dr. Ir. Endar H. Nugrahani, MS. selaku dosen penguji. Terimakasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis;
4. Semua dosen Departemen Matematika, terimakasih atas ilmu yang telah diberikani;
5. Ibu Susi, ibu Ade, bapak Yono, mas Bono, mas Heri, mas Deni dan seluruh staf pegawai Departemen Matematika, terimakasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di departemen Matematika;
6. Teman-teman satu bimbingan: Kak Danu dan Ache terimakasih buat semangatnya; 7. Kakak kelas angkatan 42 dan 41 yang tidak bisa penulis sebutkan satu per satu;
8. Teman-teman angkatan 43: Ratna yang baik, Emta, Narsih, Destya, Suci, Lia, Sophie, Resti yang udah nungguin, Margi, Agung, Fardan, Wira, Adhi, Nia, Arum, Ecka, Rias, Erni, Irsyad, Arif, Peli, Elly, Cici, Maria Herlina, Cupid, Vera, Rizky NS, Rizki SN, Nanu, Dandi, Zul, Andrew, Ucok, Kabil, Sabar, Lina, Handra, Mubarok, Faisol, Slamet, Razon, Nobo, Syahrul, Nidya. Terimakasih atas doa, dukungan dan semangatnya, terimakasih atas kebersamaannya selama 3 tahun di Math’43;
9. Adik kelas angkatan 44 dan 45 yang tidak bisa penulis sebutkan satu per satu;
10. Teman-teman Pengurus Permata 2007-2009 dan 2009-2011, terimakasih buat doa dan semangatnya;
11. Teman-teman Permata yang telah memberikan semangat dan doa serta dukungan kepada penulis dalam menyelesaikan karya ilmiah ini;
12. Bebere-bebereku : Andre, Rendy, Regina, Mima, dan Keke, terimakasih untuk canda tawanya;
13. Bang Edo, Kak Yanthi, beserta kedua bebere (Babang dan Dedek): terimakasih buat doa, semangat serta canda tawanya;
14. Teman-teman satu kosan yang tidak bisa penulis sebutkan satu per satu;
15. Friska Kembaren, terimakasih buat doa, support, dan semuanya. Aku mengasihindu;
Penulis menyadari tulisan ini masih memiliki kekurangan dan jauh dari kesempurnaan. Oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.
Semoga karya ilmiah ini bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan khususnya Matematika.
Bogor, Maret 2011
RIWAYAT HIDUP
Penulis lahir di Berastagi (Medan-Sumatra Utara) pada tanggal 20 Juli 1987 sebagai anak bungsu dari empat bersaudara, anak dari Sofian Ginting dan Rosnana Pandia.
Tahun 2000 penulis lulus dari SDN 040481 Cintarakyat. Tahun 2003 penulis lulus dari SLTPN 1 Berastagi. Tahun 2006 penulis lulus dari SMAN 1 Berastagi dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Ujian Saringan Masuk IPB (USMI). Pada tahun 2007, penulis memilih dan masuk Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
DAFTAR ISI
Halaman
DAFTAR ISI ... vii DAFTAR GAMBAR ... viii DAFTAR TABEL ... viii DAFTAR LAMPIRAN ... viii
PENDAHULUAN
1.1 Latar Belakang ... 1 1.2 Tujuan ... 1
LANDASAN TEORI
2.1 Persamaan Diferensial Linear Orde 1 ... 2 2.2 Sistem Persamaan Diferensial Mandiri ... 2 2.3 Titik Tetap ... 2 2.4 Nilai Eigen dan Vektor Eigen ... 2 2.5 Pelinearan ... 2 2.6 Kestabilan Titik Tetap ... 3 2.7 Kondisi Routh-Hurwitz ... 3 2.8 Bilangan Reproduksi Dasar (R0) ... 3
PEMBAHASAN
3.1 Perumusan Model ... 4 3.2 Titik Tetap ... 6 3.3 Titik Tetap tanpa Penyakit ... 6 3.4 Titik Tetap Endemik ... 6 3.5 Analisis Kestabilan Titik Tetap ... 6 3.5.1 Kestabilan Titik Tetap tanpa Penyakit ... 6 3.5.2 Kestabilan Titik Tetap Endemik ... 7 3.6 Dinamika Populasi Penularan Malaria ... 8 3.6.1 Dinamika Populasi untuk R0 < 1 ... 8 3.6.2 Dinamika Populasi untuk R0 > 1 ... 10
SIMPULAN ... 13
DAFTAR PUSTAKA ... 14
DAFTAR GAMBAR
Halaman 1 Diagram model penularan penyakit malaria pada manusia (yang dibagi dalam empat
kelas , ̃ , , dan ) dan populasi vektor (yang dibagi dalam dua kelas dan ̃ ) . 4 2 Dinamika populasi sh, ih, dh, dan terhadap waktu t ... 8
3 Dinamika populasi sh terhadap waktu t ... 8
4 Dinamika populasi sh, ih, dh, dan iv terhadap waktu t ... 9
5 Dinamika populasi sh terhadap waktu t ... 9
6 Dinamika populasi sh, ih, dh, dan iv terhadap waktu t ... 9
7 Dinamika populasi sh, ih, dh, dan iv terhadap waktu t ... 10
8 Dinamika populasi sh terhadap waktu t ... 10
9 Dinamika populasi sh, ih, dh, dan iv terhadap waktu t ... 11
10 Dinamika populasi sh terhadap waktu t ... 11
11 Dinamika populasi sh, ih, dh, dan iv terhadap waktu t ... 11
12 Dinamika populasi sh, ih, dh, dan ketika vektor terinfeksi 5% untuk R0 < 1 ... 12 13 Dinamika populasi sh, ih, dh, dan ketika vektor terinfeksi 50% untuk R0 < 1 ... 12
14 Dinamika populasi sh, ih, dh, dan ketika vektor terinfeksi 5% untuk R0 > 1 ... 12 15 Dinamika populasi sh, ih, dh, dan ketika vektor terinfeksi 50% untuk R0 > 1 ... 12
DAFTAR TABEL
Halaman 1 Kondisi Kestabilan Titik Tetap ... 7 2 Simulasi terhadap R0 < 1 ... 8 3 Simulasi terhadap R0 > 1 ... 10
DAFTAR LAMPIRAN
Halaman 1 Pembuktian Teorema 1 ... 15
2 Pembuktian Teorema 2 ... 15 3 Penurunan Persamaan (3.7) – (3.10) ... 16 4 Mencari Titik Tetap ... 17 5 Mencari Matriks Jacobi ... 19 6 Persamaan Karakteristik tanpa Penyakit ... 20 7 Pembuktian t2.t1-t0> 0 untuk Tanpa Penyakit ... 22
8 Mencari nilai w3, w2, w1,dan w0untuk Persamaan Karakteristik Endemik ... 22 9 Pembuktian w3.w2.w1> . dan w3, w1,dan w0 > 0 untuk Endemik ... 23 10 Nilai Eigen Titik Tetap Bebas Endemik ... 24 11 Program Mathematica 7 untuk Gambar Dinamika Populasi untuk R0 = 0.00378437 ... 25 12 Program Mathematica 7 untuk Gambar Simulasi Populasi sh ... 26
13 Program Mathematica 7 untuk Gambar Dinamika Populasi untuk R0 = 0.000105122 ... 27 14 Program Mathematica 7 untuk Gambar Simulasi Populasi sh ... 27
16 Program Mathematica 7 untuk Gambar Dinamika Populasi untuk R0 = 1.48298 ... 29 17 Program Mathematica 7 untuk Gambar Simulasi Populasi sh ... 29
18 Program Mathematica 7 untuk Gambar Dinamika Populasi untuk R0 = 5.93191 ... 30 19 Program Mathematica 7 untuk Gambar Simulasi Populasi sh ... 31
20 Program Mathematica 7 untuk Gambar Dinamika Populasi untuk R0 = 1.4837 ... 32 21 Program Mathematica 7 untuk Gambar Dinamika populasi ketika vektor awal
terinfeksi 5% untuk R0 < 1 ... 32 22 Program Mathematica 7 untuk Gambar Dinamika populasi ketika vektor awal
terinfeksi 50% untuk R0 < 1... 33 23 Program Mathematica 7 untuk Gambar Dinamika populasi ketika vektor awal
terinfeksi 5% untuk R0 > 1... 33 24 Program Mathematica 7 untuk Gambar Dinamika populasi ketika vektor awal
I PENDAHULUAN
1.1 Latar Belakang
Malaria telah diketahui sejak dahulu kala dan demam dikenal sebagai tanda orang yang akan terjangkit penyakit ini. Hal ini ditulis dalam sejarah tulisan Mesir kuno yang mengemukakan bahwa penyakit malaria disebabkan oleh parasit dari genus Plasmodium
yang dapat ditemukan pada burung, mamalia dan kadal, dimana proses penularannya melalui gigitan nyamuk Anopheles. Protozoa parasit jenis ini banyak sekali tersebar di wilayah tropik, misalnya di Amerika, Asia dan Afrika. Terdapat empat jenis parasit malaria yaitu,
Plasmodium vivax, Plasmodium falciparum,
Plasmodium ovale, dan Plasmodium malariae
dan lebih dari 3 ratus juta kasus malaria per tahun dengan 1 sampai 1,5 juta kasus kematian setiap tahunnya (kebanyakan terjadi pada anak-anak).
Dalam karya ilmiah ini akan dibahas suatu model SIDRS (Susceptible Infected Dormant
Removed Susceptible) dari penularan penyakit
malaria dalam suatu populasi. Terdapat 247 juta kasus malaria di dunia dan lebih dari satu juta kasus kematian setiap tahunnya (WHO, 2010). Pada kasus ini akan dibahas mengenai penyebaran penyakit malaria di Thailand. Malaria di Thailand ditemukan di sepanjang perbatasan Burma, Kamboja, dan Malaysia. Infeksi yang timbul dari Plasmodium
falciparum, Plasmodium vivax dan Plasmodium
malariae masing-masing berkembang menjadi
50-60%, 40-50% dan kurang dari 1%. Sedangkan Plasmodium ovale tidak ditemukan di Thailand. Di antara ketiga masalah malaria di atas yang menjadi permasalahan yang sangat besar ditemukan pada kasus Plasmodium vivax.
Pada tahun 1994 ditemukan 109.321 kasus malaria dan 45.123 di antaranya merupakan kasus malaria yang diakibatkan oleh
Plasmodium vivax.
Parasit malaria memiliki siklus kehidupan ganda yang sangat rumit, yaitu siklus reproduksi seksual terjadi pada tubuh nyamuk sendiri sedangkan reproduksi aseksualnya terjadi pada manusia. Pada reproduksi aseksual, terdapat
tahapan yang disebut tahap berenang bebas yakni tahap sporozoite. Parasit malaria dalam tahap ini akan diinfeksikan ke dalam aliran darah manusia melalui kulit manusia oleh nyamuk. Sporozoite ini akhirnya memasuki sel darah merah manusia, dimana bentuk awalnya ialah seperti cincin dan seperti bentuk amuba sebelum terjadi tahap pembelahan yang akan menjadi bentuk yang lebih kecil yang disebut
merozoite. Sel darah merah yang mengandung
merozoite ini kemudian akan pecah dan
melepaskan merozoite tersebut ke dalam aliran darah. Pada tahap ini penderita akan menggigil dan demam yang merupakan ciri khas dari penyakit malaria. Merozoite-merozoite ini akan menginfeksi sel-sel darah merah yang lain dan membangun siklus yang berulang.
Lebih dari dua milyar orang atau total 41% dari populasi dunia tinggal di daerah dimana malaria ditularkan secara teratur (misalnya, bagia Afrika, Timur Tengah, Amerika Selatan, Hispania dan Oseania) dan ada sekitar 1,5-2,7 juta orang yang meninggal akibat malaria setiap tahun. Perkembangan Plasmodium vivax
berbeda dengan Plasmodium falciparum yakni seseorang yang menderita Plasmodium
falciparum akan sembuh dari kesehatan yang
paling buruk (jika tidak meninggal), namun seorang yang terinfeksi Plasmodium vivax tidak akan meninggal namun akan tetap menderita kambuh.
1.2 Tujuan
Tujuan penulisan karya ilmiah ini adalah :
1. Mempelajari model matematika dari sistem penularan penyakit malaria dalam suatu populasi.
2. Menganalisis titik tetap yang diperoleh. 3. Melakukan simulasi terhadap model
yang diberikan sehingga terlihat parameter yang mempengaruhi populasi.
II LANDASAN TEORI
2.1 Persamaan Diferensial Linear Orde 1 Suatu persamaan yang dinyatakan sebagai
g , .
disebut persamaan diferensial (PD) linear orde 1. Jika g(t) = 0, PD disebut PD homogen dan jika g(t) ≠ 0, PD disebut PD linear tak homogen.
(Tu 1994)
2.2 Sistem Persamaan Diferensial Mandiri Suatu persamaan diferensial (SPD) dinyatakan sebagai
, . dengan f fungsi kontinu bernilai real dari x dan mempunyai turunan parsial kontinu. SPD tersebut disebut SPD mandiri (autonomous) bilamana tidak memuat waktu (t) secara eksplisit di dalamnya. tetap disebut juga titik kritis atau titik keseimbangan. Untuk selanjutnya akan digunakan istilah titik tetap.
(Tu 1994)
2.4 Nilai Eigen dan Vektor Eigen
Diberikan matriks koefisien konstan A berukuran n x n, dengan SPD homogen berikut , = , (2.3) Suatu vektor tak nol x dalam ruang
disebut vektor eigen dari A jika untuk suatu
skalar berlaku
Ax = λx (2.4) Nilai skalar dinamakan nilai eigen dari A. Untuk mencari nilai dari matriks A, maka persamaan (4) dapat ditulis kembali sebagai ( A- I )x = 0 (2.5) dengan I matriks identitas. Persamaan (2.5) mempunyai solusi tak nol jika dan hanya jika
p( ) = det( A- λI ) = │A- I│= 0 (2.6) Persamaan (6) disebut persamaan karakteristik dari matriks A. sehingga didapat persamaan linear
2.6 Kestabilan Titik tetap Diberikan SPD sebarang
, . (2.8)
Tentukan titik tetap yang memenuhi
f . Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigennya, yaitu :λidimana i = 1,2,…,n yang diperoleh dari
persamaan karakteristik (2.5).
Secara umum kestabilan titik tetap mempunyai tiga perilaku :
2. Tak Stabil, jika terdapat paling
sedikit satu i dimana Re(λi ) > 0.
3. Sadel, jika perkalian dua buah nilai eigen sembarang adalah negatif (λiλj <
0 untuk i dan j sembarang).
(Tu 1994)
2.7 Kondisi Routh Hurwitz
Misalkan a1, a2,…, ak bilangan-bilangan real, aj
= 0 jika j > k. Semua nilai eigen dari persamaan karakteristik
p(λ) = λk +a1λk-1 +…+ ak-2 λ2 + ak-1 λ1 + ak = 0
mempunyai bagian real yang negatif jika dan hanya jika determinan dari matriks i x i, untuk
Sehingga menurut kondisi Routh-Hurwitz, untuk suatu k, k = 2, 3, 4 disebutkan bahwa titik tetap
Hurwitz disajikan pada teorema 1 dan 2 berikut.
Teorema 1
Misalkan A, B, C bilangan real. Bagian real dari setiap nilai eigen persamaan karakteristik
p( λ) = λ3 +A λ2 + Bλ + C = 0 (2.9) adalah negatif jika dan hanya jika A > 0, C > 0 dan AB > C.
Teorema 2
Misalkan A,B,C dan D bilangan real. Bagian real dari setiap nilai eigen persamaan karakteristik
Bilangan Reproduksi Dasar ditulis R0 adalah
nilai harapan dari kasus kedua yang dihasilkan pada suatu populasi yang seluruhnya rentan oleh suatu jenis individu yang terinfeksi/menular. Kondisi yang timbul adalah :
1. Jika R0 < 1, maka setiap individu yang menular akan menginfeksi kurang dari satu individu baru dan penyakit tidak akan berkembang.
2. Jika R0 > 1, maka setiap individu yang menular akan menginfeksi lebih dari satu individu baru, dan penyakit tersebut dapat menyerang populasi sehingga menjadi wabah.
3.1 Perumusan Model
Model yang akan dibahas dalam karya ilmiah ini adalah model SIDRS (Susceptible
Infected Dormant Removed Susceptible) dari
penularan penyakit malaria dalam suatu populasi. Dalam model ini terdapat tiga populasi yang berbeda yaitu rentan S(t), terinfeksi I(t), dan sembuh R(t).S(t) digunakan untuk mewakili jumlah orang yang belum terinfeksi oleh penyakit pada waktu t, atau mereka yang rentan terhadap penyakit. I(t) menunjukkan jumlah individu yang telah terinfeksi oleh penyakit dan mampu menyebarkan penyakit kepada mereka yang masuk dalam kategori rentan. R(t) digunakan untuk menunjukkan banyaknya orang-orang yang telah terinfeksi dan kemudian pulih dari penyakit.
Secara skematik, diagram alur model SIDRS pada penularan penyakit malaria dalam suatu populasi ditunjukkan pada diagram kompartemen di bawah (Gambar 1). Misalkan jumlah populasi pada waktu t dinyatakan dengan N = Nh(t). Populasi ini dibagi menjadi
digolongkan ke kelas rentan ( ) dengan laju
kelahiran sebesar C. Individu yang berada di kelas rentan akan mengalami kematian dengan laju kematian sebesar , atau masuk ke kelas terinfeksi ( ) karena terjangkit plasmodium
falciparum ( ′) dan plasmodium vivax ( ′).
Laju penularan individu dari kelas rentan ( ) ke kelas Dorman ( ) karena terjangkit
plasmodium vivax namun tidak terlihat gejala
sebesar . Selanjutnya individu yang berada di kelas terinfeksi akan mati dengan laju kematian sebesar , atau sembuh dan masuk ke kelas rentan karena tidak adanya sistem kekebalan tubuh dengan laju atau sembuh dengan laju penyembuhan sebesar sehingga dimasukkan ke kelas sembuh ( ). Kemudian individu di kelas sembuh akan mati dengan laju kematian sebesar , atau menjadi rentan kembali karena sistem kekebalan tubuh dapat hilang sehingga kembali masuk ke kelas rentan dengan laju hilangnya kekebalan tubuh sebesar . Individu yang berada pada kelas Dorman ( ) akan mengalami kematian dengan laju atau sewaktu-waktu dapat kehilangan kekebalan tubuh dan masuk ke kelas terinfeksi dengan laju r3 atau sembuh namun
kehilangan kekebalan tubuh dengan laju r4 dan
menjadi rentan kembali sehingga siap untuk terinfeksi.
Selain itu, pada diagram kompartemen di atas (Gambar 1) terdapat diagram alur yang
menjelaskan populasi vektor yang membawa virus malaria. Diagram ini akan menunjukkan 2 Gambar 1 Diagram model penularan penyakit malaria pada manusia (yang dibagi dalam empat
kelas , ̃ , , dan ) dan populasi vektor (yang dibagi dalam dua kelas dan ̃ )
̃
kelas yang berbeda yakni kelas rentan S = (t) yakni ditujukan kepada populasi vektor yang masih steril dari virus malaria dan kelas infeksi
I = (t) yaitu ditujukan kepada vektor yang sudah terinfeksi oleh virus malaria. Total populasi vektor dinyatakan dengan NV = +
. Vektor yang lahir digolongkan ke dalam populasi rentan ( ) dengan laju kelahiran A. Vektor yang berada di kelas rentan akan mengalami kematian dengan laju μv , atau masuk ke kelas terinfeksi ( ) dengan laju
.
Selanjutnya vektor yang berada pada kelas terinfeksi akan mengalami kematian dengan laju μv. Laju perubahan populasi manusia atau vektor pada suatu kelas ialah jumlah manusia atau vektor yang masuk dalam kelas tersebut dikurangi dengan jumlah manusia atau vektor yang meninggalkan kelas tersebut. Penjelasan di atas dapat dituliskan dalam bentuk persamaan-persamaan berikut:
µh adalah laju kematian populasi
µv adalah laju kematian vektor
adalah laju penularan P.falciparum dari nyamuk ke tubuh manusia
adalah laju penularan P.vivax dari nyamuk ke tubuh manusia
adalah laju penularan P.falciparum dari tubuh manusia ke tubuh nyamuk
adalah laju penularan P.vivax dari tubuh manusia ke tubuh nyamuk
adalah laju kelahiran populasi
Nh adalah total banyaknya populasi
α adalah rasio dorman manusia yang terinfeksi
adalah tingkat dimana seseorang terinfeksi P.falciparum
adalah tingkat dimana seseorang terinfeksi P.vivax
adalah tingkat dimana manusia tidak aktif namun akan kambuh kembali adalah laju pemulihan manusia yang dorman oleh P.vivax
adalah tingkat pemulihan manusia dan akan menjadi manusia yang rentan adalah laju pemulihan manusia dari infeksi P.falciparum
adalah laju pemulihan manusia dari infeksi P.vivax
(t) adalah banyaknya vektor rentan (t) adalah banyaknya vektor menular
dengan kondisi sh+ih+dh+rh=1 dan sv+iv=1, dan ,
,
Selanjutnya akan dicari titik tetap untuk persamaan (3.7), (3.8), (3.9), dan (3.10) yang kemudian akan dianalisis kestabilan di sekitar titik tetap tersebut serta dinamika populasinya.
3.2 Titik Tetap
Analisis titik tetap pada SPD sering digunakan untuk menentukan suatu solusi konstan. Titik tetap dari persamaan .
. akan diperoleh dengan menetapkan
sh(t) = 0, ih(t)= 0, dh(t) = 0 dan
iv(t) sehingga diperoleh
persamaan-persamaan di bawah ini:
(i) persamaan di atas secara serentak akan diperoleh dua titik tetap yaitu titik tetap tanpa penyakit dan titik tetap endemik.
3.3 Titik Tetap tanpa Penyakit
Titik tetap tanpa penyakit merupakan kondisi dimana semua individu sehat dan tetap sehat tiap waktu dengan kata lain tidak terdapat penyakit. Titik tetap ini diperoleh ketika banyaknya vektor yang terinfeksi sama dengan nol ( ) yang didapat dari persamaan (iv), kemudian disubstitusi ke persamaan (i), (ii), dan (iii) maka akan diperoleh nilai , , dan sehingga diperoleh titik tetap dari persamaan-persamaan (3.7), (3.8), (3.9), dan (3.10) yaitu , , , .
3.4 Titik Tetap Endemik
Pada titik tetap endemik akan menghasilkan solusi nontrivial. Di sini titik tetap endemik merupakan kondisi dimana penyakit masih terdapat di dalam populasi
vektor dan manusia. Dari persamaan (19), (20), (21), dan (22) diperoleh titik tetap endemik
E1 = (sh*,ih*,dh*,iv*) dengan
3.5. Analisis Kestabilan Titik Tetap
Misalkan persamaan (3.7)-(3.10) dituliskan sebagai berikut :
sh(t) = A(sh, ih, dh, iv)
ih(t) = B(sh, ih, dh, iv)
dh(t)= C(sh, ih, dh, iv)
iv(t)= D(sh, ih, dh, iv)
Dari persamaan di atas dapat diperoleh matriks
Jacobi.
J0 =
=
dengan,
J = { } untuk I = 1, 2, 3, 4 dan j =1, 2, 3, 4
3.5.1 Kestabilan Titik Tetap tanpa Penyakit Pelinearan pada titik tetap akan menghasilkan matriks Jacobi sebagai berikut:
Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik
det J . Persamaan
karakteristik dari J adalah ( +µ + ) ( t t t ) = 0 sehingga diperoleh salah satu nilai eigen dari J yaitu = µ r dan nilai eigen yang lainnya diperoleh dari akar polinomial
Karena semua parameter yang terlibat positif maka t , , dan t
sehingga kestabilan di titik bergantung pada nilai . Kondisi akan terpenuhi ketika R0 < 1 maka titik tetap stabil dan sebaliknya kondisi tidak dipenuhi ketika
R0> 1 maka titik tetap sadel. Kondisi stabil
yang dipenuhi ketika R0 < 1 dimana R0 merupakan bilangan reproduksi dasar virus dalam populasi , sehingga ketika
merupakan kondisi stabil asimtotik karena virus malaria tidak dapat bertahan dalam populasi. Sebaliknya, ketika merupakan kondisi tidak stabil karena virus malaria dapat bertahan dan meningkat dalam populasi. Sehingga menurut kriteria Routh-Hurwitz, titik E0 stabil.
3.5.2 Kestabilan Titik Tetap Endemik
Pelinearan pada titik tetap akan menghasilkan matriks Jacobi sebagai berikut:
J1 =
Untuk memperoleh nilai eigen digunakan persamaan karakteristik det J . Persamaan karakteristik dari J adalah
w w w w dan nilai
eigennya diperoleh dari akar polinomial p( λ) = λ4
+w3 λ3 + w2 λ2 + w1λ + w0 = 0. Karena
semua parameter yang terlibat positif maka
w , , dan dengan
menggunakan software Mathematica dibuktikan
w sehingga menurut
Routh-Hurwitz, titik stabil.
Berikut ini adalah tabel kondisi kestabilan dari kedua titik tetap yang diperoleh.
Tabel 1 Kondisi kestabilan titik tetap.
Kondisi
Simpul stabil
Spiral Tidak stabil
Sadel Spiral stabil
Dari Tabel 1 dapat dilihat bahwa kondisi kestabilan dari titik tetap yang diperoleh saling bertentangan. Ketika titik tetap yang pertama stabil, titik tetap yang kedua tidak stabil dan ketika titik tetap yang pertama tidak stabil, titik tetap yang kedua stabil.
0 200 400 600 800 1000 1200 1400 0.0 3.6 Dinamika Populasi Penularan Malaria
Untuk mengamati pengaruh masuknya virus malaria ke dalam populasi manusia maupun vektor pada waktu tertentu maka diperlukan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi dengan variabel waktu. Hal ini membutuhkan nilai awal untuk semua parameter dan variabel.
Pada proses penggambarannya diambil nilai awal populasi nyamuk atau vektor yang terinfeksi adalah 5% dari total populasi nyamuk.
Dalam karya ilmiah ini dianalisis dinamika populasi untuk dua kondisi yaitu
di mana populasi akan stabil karena penyakit hilang dari populasi dan di mana penyakit bertahan dalam populasi dan meningkat menjadi wabah.
3.6.1 Dinamika Populasi untuk
Proses penggambarannya dengan menggunakan Mathematica 7 yang dievaluasi ketika ditetapkan h = 0.0000421 per hari yang sesuai dengan harapan hidup yang sesungguhnya dari 65 tahun untuk manusia, dan
V = 1/30, yang sesuai dengan harapan hidup dari 30 hari untuk nyamuk Anopheles. Nilai-nilai = 1/20 per hari dan = 1/14 per hari, sesuai dengan waktu yang dibutuhkan orang manusia yang terinfeksi dengan P. falciparum
dan P.vivax untuk meninggalkan kelas
terinfeksi dan menjadi rentan kembali, yaitu 20 hari untuk P. falciparum dan 14 hari untuk P .
vivax. Nilai-nilai = 1/365 per hari, =
1/(2*365) per hari sesuai dengan waktu yang dibutuhkan orang yang terinfeksi P.vivax untuk meninggalkan kelas dorman, yaitu 1 tahun untuk memasuki kelas yang terinfeksi , dan 2 tahun untuk memasuki kelas rentan. Nilai =1/(3*365) per hari sesuai dengan 3 tahun bagi orang-orang yang terinfeksi dengan P.vivax
akan kehilangan sistem imun. Nilai-nilai = 1 / 30 per hari, = 1 / 25 per hari sesuai dengan waktu yang dibutuhkan orang-orang yang terinfeksi P.falciparum dan P.vivax untuk pulih, yakni 30 hari untuk P.falciparum dan 25 hari untuk P.vivax, α = 0.65. Untuk mendapatkan titik tetap pada keadaan bebas penyakit yang stabil lokal, kita menetapkan masing-masing , , , sama dengan 0.025, 0.024, 0.03 dan 0.02.
Untuk nilai dilakukan analisis untuk tiga kondisi yang berbeda dengan
mengubah nilai (laju kematian vektor) dan α (rasio dorman manusia yang terinfeksi) seperti yang ditunjukkan pada tabel berikut.
Tabel 2 Simulasi terhadap Ro < 1. μv
. 0.65 0.003784437
. 0.65 0.000105122
0.033 0.00065 0.00378044
a. .
Kondisi . dipenuhi
ketika = 0.033 dan α = 0.65. Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,
Gambar 2 Dinamika populasi , . , dan terhadap waktu t.
Pada gambar di bawah ini akan dilakukan simulasi populasi Sh terhadap waktu t dengan
0 200 400 600 800 1000 1200 1400
0.0
0 200 400 600 800 1000 1200 1400 0.0
ketika rasio jumlah manusia yang terinfeksi virus tetap dengan α = 0.65 dan laju kematian murni pada vektor dinaikkan menjadi . sehingga diperoleh gambar dinamika populasi di bawah ini,
Gambar 4 Dinamika populasi , . , dan terhadap waktu t.
Pada gambar di bawah ini akan dilakukan simulasi populasi Sh terhadap waktu t dengan
mengubah nilai parameter dan .
Gambar 5 Dinamika populasi sh terhadap
waktu t.
c. .
Kondisi . dipenuhi ketika rasio jumlah manusia yang terinfeksi virus diturunkan menjadi α = 0.00065 dan laju kematian murni pada vektor tetap . sehingga diperoleh gambar dinamika populasi di bawah ini,
Gambar 6 Dinamika populasi , . , dan terhadap waktu t.
Pada Gambar 2, Gambar 4 dan Gambar 6 dapat dilihat bahwa kurva Sh stabil naik menuju
satu, namun pada kurva Ih stabil turun menuju
ke nol. Hal ini berarti bahwa banyaknya manusia yang terinfeksi akan mengurangi banyaknya manusia yang rentan karena total populasi dianggap konstan. Penurunan pada kurva mengakibatkan penurunan pada kurva
Ih, hal ini dikarenakan semakin sedikit jumlah
nyamuk yang terinfeksi sehingga jumlah manusia yang terinfeksi pun semakin sedikit. Pada kurva Dh dapat kita lihat awalnya
mengalami sedikit kenaikan dan kemudian stabil turun menuju kepunahan. Hal ini berarti semakin sedikit jumlah nyamuk yang terinfeksi sehingga jumlah manusia yang dorman pun semakin sedikit. Pada Gambar 2, Gambar 4 dan Gambar 6 dilakukan simulasi dengan mengubah nilai parameter dan . Jika nilai
semakin besar maka jumlah manusia yang rentan akan semakin besar dan jika nilai
semakin kecil maka akan terjadi penurunan pada jumlah manusia rentan. Jika nilai semakin besar maka jumlah manusia rentan akan semakin kecil.
Gambar 3 dan Gambar 5 menunjukkan hubungan populasi Sh terhadap waktu t. Ketiga
kurva di atas dibandingkan berdasarkan nilai ′ dan ′ yang berbeda yaitu ′ = 0.025 dan
′ = 0.024, ′ = 0.045 dan ′ = 0.056, ′ =
0.060 dan ′ = 0.075. Dari kurva di atas dapat dilihat bahwa manusia yang rentan mengalami terus penaikan yang tajam menuju satu yang artinya menuju kestabilan. Semakin besar nilai
′ dan ′, kurva akan mengalami penaikan
ketika laju penularan Plasmodium falciparum
dan Plasmodium vivax dari nyamuk ke tubuh
manusia meningkat ′ dan ′ mengakibatkan banyaknya manusia yang rentan menurun.
3.6.2 Dinamika Populasi untuk
Proses penggambarannya dengan menggunakan Mathematica 7 yang dievaluasi ketika ditetapkan h = 0.0000421 per hari yang sesuai dengan harapan hidup yang sesungguhnya dari 65 tahun untuk manusia, dan
V = 1/120, yang sesuai dengan harapan hidup dari 30 hari untuk nyamuk Anopheles. Nilai-nilai = 1/20 per hari dan = 1/14 per hari, sesuai dengan waktu yang dibutuhkan orang manusia yang terinfeksi dengan P. falciparum
dan P.vivax untuk meninggalkan kelas
terinfeksi dan menjadi rentan kembali, yaitu 20 hari untuk P. falciparum dan 14 hari untuk P .
vivax. Nilai-nilai = 1/365 per hari, =
1/(2*365) per hari sesuai dengan waktu yang dibutuhkan orang yang terinfeksi P.vivax untuk meninggalkan kelas dorman, yaitu 1 tahun untuk memasuki kelas yang terinfeksi , dan 2 tahun untuk memasuki kelas rentan. Nilai =1/(3*365) per hari sesuai dengan 3 tahun bagi orang-orang yang terinfeksi dengan P.vivax
akan kehilangan sistem imun. Nilai-nilai = 1 / 30 per hari, = 1 / 25 per hari sesuai dengan waktu yang dibutuhkan orang-orang yang terinfeksi P.falciparum dan P.vivax untuk pulih, yakni 30 hari untuk P.falciparum dan 25 hari untuk P.vivax, α = 0.70. Untuk mendapatkan titik tetap pada keadaan endemik yang stabil lokal, kita menetapkan masing-masing , , , sama dengan 0.14, 0.1, 0.15 dan 0.1.
Untuk nilai dilakukan analisis untuk tiga kondisi yang berbeda dengan mengubah nilai (laju kematian vektor) dan α (rasio dorman manusia yang terinfeksi) seperti yang ditunjukkan pada tabel berikut.
Tabel 3 Simulasi terhadap Ro >1.
μv
. 0.70 1.448298
. 075 5.93191
0.0084 0.9999 1.4837
a. .
Kondisi . dipenuhi ketika = 0.0084 dan α = 0.70. Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,
Gambar 7 Dinamika populasi , . , dan terhadap waktu t.
Pada gambar di bawah ini akan dilakukan simulasi populasi Sh terhadap waktu t dengan
mengubah nilai parameter dan .
Gambar 8 Dinamika populasi sh terhadap