Metode Branch and Bound (AND/OR) pada Load Balancing
Teks penuh
Gambar
Dokumen terkait
Dengan penentuan asupan gizi maksimal pada tiap simpulnya, proses pencarian akan membawa kita pada solusi yang optimum, karena tidak semua objek pada permasalahan ini dapat dimasukan
Tujuan penelitian ini adalah untuk menentukan batas bawah dari metode branch and price pada program bilangan bulat sehingga dapat mencapai solusi optimal... 1.5
Adapun tujuan dari penelitian ini adalah untuk menentukan solusi optimal penentuan truk pengangkut sampah pada Dinas Kebersihan dan Pertamanan Kota Padang dengan menggunakan
Pendekatan solusi dari suatu masalah optimisasi Diskrit atau Kombinatorik dapat diperoleh dengan menggunakan metode Branch & Bound secara langsung pada permasalahan
Penyelesaian dari metode Branch and Bound ialah untuk mencari solusi optimal yang dilakukan secara berulang hingga membentuk pohon pencarian (search tree) dan dilakukan
Tabel 1 menyajikan nilai fungsi objektif dari solusi optimal, jumlah iterasi dan percabangan, serta waktu yang dibutuhkan CPU untuk menyelesaikan perhitungan yang
Metode Branch and Bound merupakan metode baku untuk menyelesaikan problema PITL, akan tetapi secara komputasi tidak efisien karena subproblema harus diselesaikan pada setiap
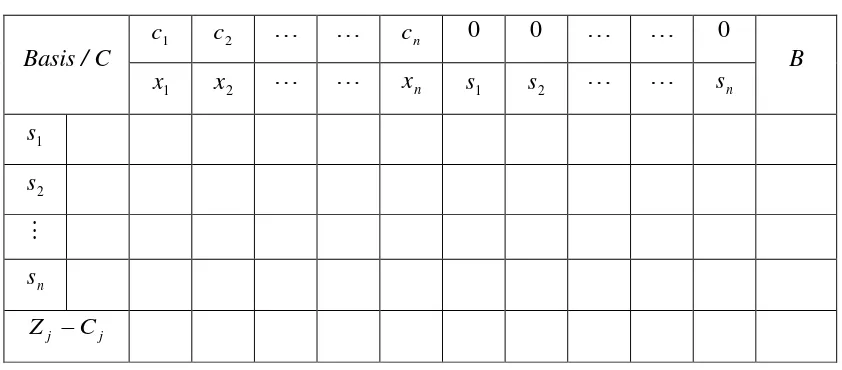
Kendala diubah menjadi bentuk persamaan, dengan menambahkan variabel slack untuk kendala bertanda ≤, untuk kendala bertanda ≥ dikurangi dengan surplus dan untuk kendala bertanda = maka