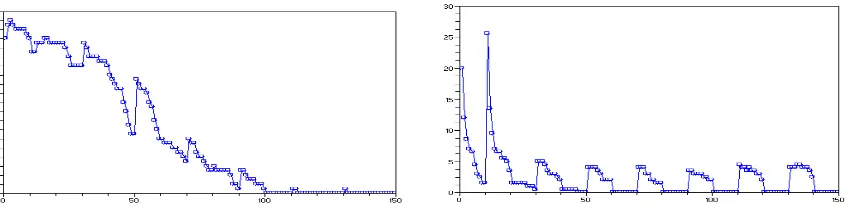
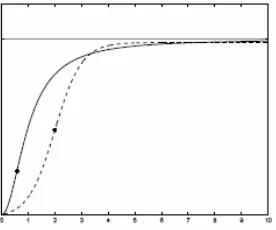
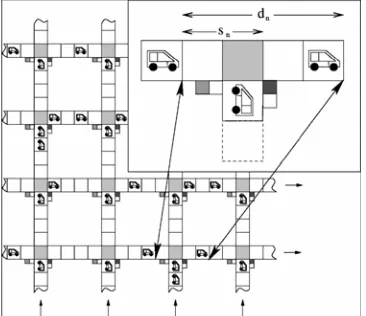
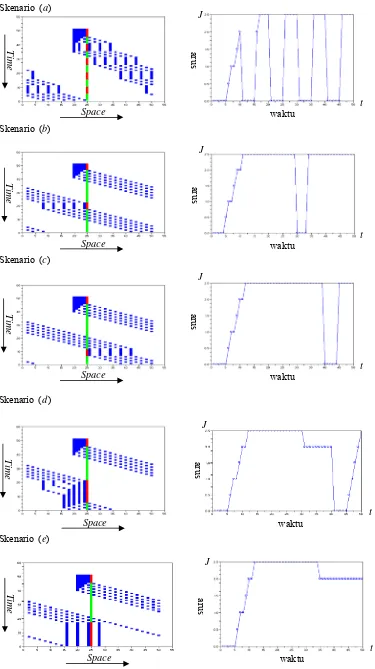
Traffic Light Strategies in Optimizing the Traffic Flow
Teks penuh
Gambar
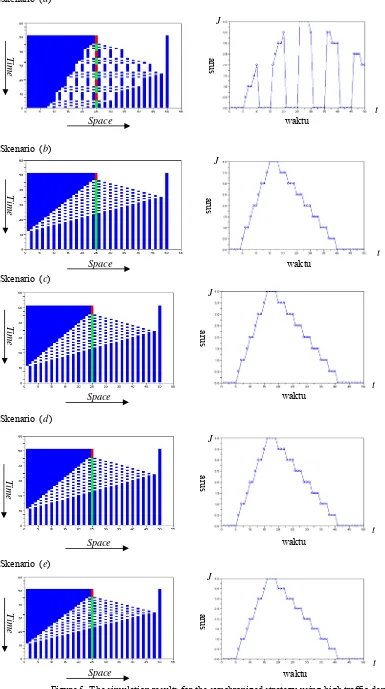
Dokumen terkait
Berdasarkan visi dan misi yang dimiliki perusahaan agar bisa menetukan strategi bersaing yang tepat Batik Gres Tenan perlu mempelajari faktor internal dan
Terdapat pengaruh PDRB, Upah minimum dan Inflasi secara bersama-sama terhadap tingkat Pengangguran terbuka di Provinsi Jawa Tengah sebesar 90.9% dan sisanya
Pendugaan faktor-faktor berpengaruh terhadap tingkat kesejahteraan dengan menggunakan model regresi logistik binari menunjukkan bahwa variabel demografi (jumlah keluarga, umur
puisi kita saat ini berada pada jalur konvensi puisi modern, terlihat dalam dalam puisi-puisi tersebut terdapat adanya hubungan manusia dengan Tuhan tampak menonjol dalam
eustachius, infeksi bakteri atau virus pada telinga tengah, peradangan nasal karena.. rinitis alergi atau karena infeksi virus saluran pernafasan
RahmatNya tiada terbatas sehingga kami dapat menyelesaikan tugas penyusunan Karya Tulis Ilmiah dengan judul “Hubungan Pengetahuan Tentang Pemilihan Makanan Jajanan
Peta Jenis Tanah dan Penggunaan Lahan Kecamatan Tuntang Kabupaten Semarang Skala 1:100.000 Kenampakan Penggunaan Lahan Sawah Pada Jenis Tanah Latosol Coklat Tua Desa
yang banyak ditumbuhi mangrove dan merupakan kawasan hutan mangrove yang dilindungi, karena banyak memberikan manfaat langsung maupun tidak langsung bagi kehidupan