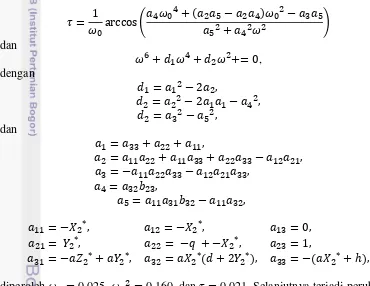DINAMIKA MODEL POPULASI SPESIES TUNGGAL PADA
LINGKUNGAN TERCEMAR DENGAN WAKTU TUNDA
TUNGGAL DISKRET
LAILATUL QODARIAH
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Dinamika Model Populasi Spesies Tunggal pada Lingkungan Tercemar dengan Waktu Tunda Tunggal Diskret adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
LAILATUL QODARIAH. Dinamika Model Populasi Spesies Tunggal pada Lingkungan Tercemar dengan Waktu Tunda Tunggal Diskret. Dibimbing oleh ELIS KHATIZAH dan ALI KUSNANTO.
Dalam karya ilmiah ini dijelaskan tentang model populasi spesies tunggal pada lingkungan tercemar. Dalam model ini dipelajari perilaku kestabilan populasi spesies tunggal yang terkena efek polutan akibat pencemaran lingkungan. Perilaku kestabilan yang dipelajari adalah perilaku kestabilan yang dibatasi, yaitu perilaku kestabilan model ketika tidak ada penambahan polutan eksogen ke dalam lingkungan tercemar dan ketika ada penambahan polutan eksogen ke dalam lingkungan tercemar. Pada kondisi titik tetap tertentu, perilaku kestabilan lokal ditentukan dengan kriteria Routh-Hurwitz dan perilaku kestabilan global dianalisis menggunakan fungsi Lyapunov. Mengubah nilai-nilai parameter sistem seperti parameter penambahan polutan eksogen ke dalam lingkungan tercemar akan memunculkan bifurkasi Hopf. Keberadaan bifurkasi Hopf dianalisis menggunakan kriteria Liu yang berkaitan dengan kriteria Routh-Hurwitz. Model populasi spesies tunggal pada karya ilmiah ini juga mempelajari efek waktu tunda tunggal diskret sebagai realisasi bahwa penyerapan polutan oleh populasi dari lingkungan tercemar tidak seketika terserap oleh populasi, melainkan membutuhkan waktu hingga akhirnya mencemari populasi. Panjang waktu tunda ditentukan menggunakan kriteria Nyquist sebagai upaya mempertahankan kestabilan model. Simulasi menggunakan software matematika digunakan sebagai upaya mengilustrasikan hasil analisis model.
Kata kunci: bifurkasi Hopf, spesies tunggal, waktu tunda.
ABSTRACT
LAILATUL QODARIAH. The Dynamics of a Single-Species Population in a Polluted Environment with Single Discrete Time Delay. Supervised by ELIS KHATIZAH dan ALI KUSNANTO.
Changing the value of parameters system such as the parameter of additional of exogenous pollutants into the polluted environment will trigger Hopf bifurcation existence. The occurrence of Hopf bifurcation was analyzed by Liu criterion that related to the Routh-Hurwitz criterion. A single-species population model in this manuscript also describes the effect of a single discrete time delay as a realization that the absorption of pollutants was not immediately absorbed by the population, but needing a time to contaminate the population. Furthermore, the time delay was estimated by using the Nyquist criterion in order to maintain the stability of the model. Mathematical simulation using a software was used to illustrate the results of models analysis.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
DINAMIKA MODEL POPULASI SPESIES TUNGGAL PADA
LINGKUNGAN TERCEMAR DENGAN WAKTU TUNDA
TUNGGAL DISKRET
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2014
Judul Skripsi : Dinamika Model Populasi Spesies Tunggal pada Lingkungan Tercemar dengan Waktu Tunda Tunggal Diskret
Nama : Lailatul Qodariah NIM : G54100016
Disetujui oleh
Elis Khatizah, MSi Pembimbing I
Drs Ali Kusnanto, MSi Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Judul yang dipilih dalam studi pustaka yang dilaksanakan sejak bulan Januari 2014 ini ialah Dinamika Model Populasi Spesies Tunggal pada Lingkungan Tercemar dengan Waktu Tunda Tunggal Diskret.
Terima kasih penulis ucapkan kepada semua pihak yang telah membantu dalam penyelesaian karya ilmiah ini khususnya Ibu Elis Khatizah, MSi dan Bapak Drs Ali Kusnanto, MSi selaku pembimbing, serta Bapak Dr Paian Sianturi yang telah banyak memberi saran. Di samping itu, penghargaan penulis sampaikan kepada Bapak Winardi dan Ibu Masyitoh selaku orangtua yang memberikan dukungan, semangat, dan doa tanpa henti. Ungkapan terima kasih juga disampaikan kepada adik, kakak, seluruh keluarga, serta teman-teman atas segala doa, semangat, dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
DAFTAR ISI
DAFTAR GAMBAR viii
DAFTAR LAMPIRAN viii
PENDAHULUAN
Latar Belakang 1
Tujuan Penelitian 2
TINJAUAN PUSTAKA 2
HASIL DAN PEMBAHASAN 8
Model Matematika 8
Model Matematika Populasi Spesies Tunggal pada Lingkungan Tercemar
Tanpa Waktu Tunda 8
Model Matematika Populasi Spesies Tunggal pada Lingkungan Tercemar
dengan Waktu Tunda Tunggal Diskret 15
Perkiraan Panjang Waktu Tunda 20
SIMULASI MODEL TANPA WAKTU TUNDA 22
DINAMIKA MODEL DENGAN WAKTU TUNDA 32
SIMPULAN 33
DAFTAR PUSTAKA 34
LAMPIRAN 36
DAFTAR GAMBAR
1 Dinamika Populasi Spesies Tunggal untuk Model = 0 23 2 Dinamika Populasi Spesies Tunggal untuk Model > 0 dengan <
0 24
3 Dinamika Populasi Spesies Tunggal untuk Model > 0 dengan >
0 25
4 Kestabilan Global pada Titik Tetap 25
5 Dinamika Populasi Spesies Tunggal pada Lingkungan Tercemar
Berdasarkan Parameter q 26
6 Dinamika Populasi Spesies Tunggal pada Lingkungan Tercemar
Berdasarkan Parameter p 28
7 Dinamika Populasi Spesies Tunggal pada Lingkungan Tercemar
Berdasarkan Parameter 29
DAFTAR LAMPIRAN
1 Penondimensionalan Model 36
2 Penentuan Titik Tetap untuk Model = 0 37
3 Penentuan Titik Tetap untuk Model > 0 37
4 Penentuan Nilai Eigen untuk Model = 0 39
5 Penentuan Nilai Eigen untuk Model > 0 41
6 Kestabilan Global 44
7 Pelinearan Model dengan Waktu Tunda 44
8 Mencari Persamaan Karakteristik Model dengan Waktu tunda 47 9 Analisis Bifurkasi Hopf Model dengan Waktu Tunda 48 10 Transformasi Laplace pada Model dengan Waktu Tunda 49
11 Kriteria Nyquist 51
12 Kode Program Bidang Solusi 53
13 Kode Program Bidang Fase 53
PENDAHULUAN
Latar Belakang
Pencemaran lingkungan merupakan risiko yang timbul dari pesatnya perkembangan industri saat ini. Kehadiran racun atau polutan yang merupakan zat, bahan, atau unsur yang tercampur dalam lingkungan dengan kadar berlebih dapat mengubah, menghalangi, atau mengganggu fungsi lingkungan. Hal ini merupakan indikator terjadinya pencemaran lingkungan (Siahaan 2004). Fenomena pencemaran ini akan menyebabkan berkurangnya daya dukung lingkungan yang kemudian akan memengaruhi laju pertumbuhan spesies di lingkungan.
Hujan asam adalah salah satu contoh fenomena lingkungan yang menggambarkan adanya fenomena pencemaran udara. Hujan asam disebabkan oleh jenis senyawa tertentu dari polusi udara yang bercampur dengan uap air, seperti hujan atau kabut. Hujan asam ini kemudian jatuh ke bumi sebagai larutan asam dengan komponen utamanya adalah oksidasi dari Sulfur dan Nitrogen. Kedua komponen ini secara dominan dihasilkan dari pembangkit listrik pembakaran batu bara, pelumeran tembaga, pabrik, dan emisi kendaraan bermotor. Oksidasi ini berubah secara kimiawi pada atmosfer dan kembali ke bumi melalui hujan, salju, kabut atau debu. Proses pengasaman lingkungan ini dapat mengubah struktur ekologi sehingga memengaruhi komunitas ekologi (Van Lier dan Irene1980).
Beberapa tahun terakhir, masalah polusi lingkungan ini menjadi perhatian serius karena polusi dapat memengaruhi kelangsungan hidup jangka panjang dari spesies dan keanekaragaman hayati dari habitat (Siahaan 2004). Oleh karena itu, studi tentang efek dari polutan pada populasi dan penilaian risiko untuk populasi menjadi cukup penting. Masalah memperkirakan efek dari polutan pada populasi melalui model matematika merupakan cara yang efektif.
Penelitian terkait pendugaan efek polutan pada sistem ekologi menggunakan model matematika dilakukan pertama kali oleh Hallam dan rekannya pada tahun 1983 (Hallam et al. 1983). Sejak itu banyak penelitian yang mempelajari efek dari polutan pada lingkungan tercemar, termasuk Pal dan Samanta yang memaparkan model populasi spesies tunggal pada lingkungan tercemar dengan mempertimbangkan adanya kontrol pencemaran pada populasi (Pal dan Samanta 2010).
Selanjutnya, dipahami bahwa banyak proses alami atau buatan manusia pada sistem ekologi, pengobatan, proses kimia, dan proses lainnya merupakan proses yang melibatkan waktu tunda. Waktu tunda sangat sering terjadi, hampir pada semua kondisi, sehingga memedulikannya adalah memedulikan realitas (Kuang 1993). Mempertimbangkan waktu tunda dalam mempelajari efek polutan terhadap populasi pada lingkungan tercemar juga dianggap perlu. Hal ini terjadi karena polutan pada lingkungan tercemar tidak seketika terserap oleh populasi, melainkan membutuhkan waktu hingga akhirnya mencemari populasi tersebut.
2
yang disusun oleh Sharma dan Samanta (2013). Dari model ini akan dianalisis karakteristik, kestabilan, dinamika, dan perkiraan panjang waktu tunda pada populasi spesies tunggal yang dipengaruhi oleh lingkungan tercemar.
Tujuan Karya Ilmiah
Tujuan karya ilmiah ini adalah:
1. Menganalisis dinamika kestabilan dan menunjukkan adanya bifurkasi Hopf pada model matematika populasi spesies tunggal pada lingkungan tercemar tanpa waktu tunda Sharma dan Samanta (2013).
2. Menganalisis dinamika kestabilan dan menunjukkan adanya bifurkasi Hopf pada model matematika populasi spesies tunggal pada lingkungan tercemar dengan waktu tunda tunggal diskret Sharma and Samanta (2013).
3. Memperkirakan panjang waktu tunda pada model matematika populasi spesies tunggal pada lingkungan tercemar dengan waktu tunda tunggal diskret Sharma dan Samanta (2013).
TINJAUAN PUSTAKA
Diberikan fungsi persamaan diferensial sebagai berikut.
̇ (1)
Persamaan (1) disebut sistem dimensi satu atau sistem orde satu dengan x(t) adalah nilai real fungsi dari waktu dan f(x) adalah nilai real fungsi dari yang bergantung terhadap waktu. Persamaan (1) memunyai titik tetap jika memenuhi . Titik tetap disebut juga titik kritis atau titik kesetimbangan (Tu 1994).
Persamaan (1) dikatakan sistem persamaan diferensial linear jika f merupakan fungsi linear dan persamaan (1) dikatakan sistem persamaan diferensial taklinear jika f merupakan fungsi taklinear. Untuk suatu sistem persamaan diferensial taklinear, analisis kestabilannya dilakukan melalui pelinearan. Tahap pertama dalam pelinearan terhadap persamaan (1) adalah mengasumsikan persamaan (1) sebagai persamaan taklinear dengan turunan parsial dari persamaan (1) kontinu di
Rn. Menggunakan ekspansi Taylor di sekitar titik tetapnya diperoleh
̇ , (2)
dengan [
]
3 dan adalah suku berorde tinggi yang memiliki sifat (Tu 1994).
Persamaan (2) dapat dituliskan dalam bentuk ̇ .
Misalkan matriks A berukuran , maka suatu vektor taknol x di Rn disebut vektor eigen dari A, jika untuk suatu skalar , yang disebut nilai eigen dari A, berlaku
(3)
Vektor x disebut vektor eigen yang bersesuaian dengan nilai eigen. Untuk mencari nilai eigen dari matriks A yang berukuran , maka persamaan (3) dapat ditulis sebagai berikut.
(4)
dengan I adalah matriks identitas, maka persamaan (4) akan memiliki solusi taknol jika dan hanya jika
, (5)
dengan merupakan persamaan karakteristik dari A (Meiss 2007).
(Giesl 2007; Meiss 2007) menjelaskan bahwa kestabilan titik tetap dapat ditentukan dengan memperhatikan nilai-nilai eigen, yaitu yang diperoleh dari persamaan karakteristik. Secara umum, kestabilan titik tetap memunyai perilaku sebagai berikut.
1. Stabil, jika
a. untuk setiap i.
b. Terdapat ( ) untuk sembarang j dan , untuk setiap . Stabil asimtotik jika untuk setiap i. Stabil asimtotik terbagi menjadi dua, yaitu asimtotik lokal dan asimtotik global. Titik dikatakan titik tetap stabil asimtotik lokal jika hanya berlaku untuk nilai-nilai state awal di sekitar titik tetap, sedangkan titik dikatakan titik tetap stabil asimtotik global jika berlaku untuk semua nilai-nilai state awal, semua state akan bergerak menuju satu titik tetap yang sama.
2. Tidak stabil, jika terdapat paling sedikit satu i sehingga .
3. Sadel, jika perkalian dua buah nilai eigen real sembarang adalah negatif untuk i dan j sembarang). Sadel hiperbolik, jika , untuk setiap i.
4
Teorema Routh-Hurwitz Criterion 1: Misalkan bilangan-bilangan real, jika . Semua nilai dari persamaan karakteristik
, (6) memunyai bagian real yang negatif jika dan hanya jika untuk setiap i=1,2,…,k, determinan dari matriks Mi
[
]
adalah positif. Sehingga menurut kondisi Routh-Hurwitz dalam teorema 1, untuk suatu k, disebutkan bahwa titik tetap stabil asimtotik lokal jika dan hanya jika
,
Untuk kasus k = 3, kondisi Routh-Hurwitz disajikan pada teorema berikut. Teorema Routh-Hurwitz Criterion 2: Misalkan A, B, C bilangan real. Bagian real dari setiap nilai eigen persamaan karakteristik
(7)
adalah negatif jika dan hanya jika A, B, C positif dan AB > C (Fisher 1990).
Bukti:
Routh – Hurwitz criterion 2: Misalkan A, B, C adalah bilangan real, bagian real nilai eigen dari persamaan polinomial karakteristik
3 2
adalah negatif jika dan hanya jika A, C positif dan AB > C.
Dari persamaan 3 2 maka .
Menurut teorema Routh – Hurwitz criterion 2 persamaan karakteristik
3 2 memunyai bagian real nilai eigen negatif jika
| | | | | | positif, sehingga
| | | | | |
5
| | |
| |
|
karena maka
Routh – Hurwitz criterion 2 terbukti Kestabilan dapat bersifat lokal dan bersifat global. Kestabilan lokal mudah ditentukan dengan pendekatan linear. Sedangkan kestabilan global cukup sulit ditentukan. Menggunakan fungsi Lyapunov adalah salah satu metode yang dapat digunakan dalam menentukan kestabilan global. Verhulst (1990) menjelaskan bahwa fungsi Lyapunov dari suatu sistem persamaan diferensial bersifat tidak tunggal. Misal diberikan fungsi dan titik kestabilan persamaan (1). Fungsi V disebut fungsi Lyapunov jika memenuhi ketiga pernyataan berikut.
1. Fungsi V kontinu dan memunyai turunan parsial pertama yang kontinu Pada E.
2. Fungsi untuk dengan , dan = 0 dengan (dengan titik tetap merupakan titik minimum global).
3. Fungsi ̇ untuk setiap .
L o ’ (2009) memberikan fungsi Lyapunov yang memenuhi ketiga pernyataan di atas.
1. Fungsi Lyapunov logaritma diperkenalkan oleh Goh untuk sistem Lokta-Volterra
∑
( )
2. Fungsi Lyapunov kuadratik umum (common quadratic Lyapunov functions)
∑
3. Fungsi Lyapunov kuadratik gabungan (composite quadratic Lyapunov function)
[∑
]
Titik kestabilan sistem persamaan (1) dikatakan memiliki kestabilan global jika terdapat fungsi Lyapunov V dengan titik tetap sehingga,
6
3. Terdapat M himpunan invarian terbesar dalam { | ̇ }, maka setiap solusi x(t) menuju ke M untuk .
Persamaan diferensial dengan waktu tunda merupakan salah satu bentuk persamaan diferensial dimana turunan dari fungsi yang tidak diketahui berapa waktu tunda yang diberikan. Hal ini berkaitan dengan nilai dari fungsi waktu yang dibutuhkan suatu proses. Bentuk umum persamaan diferensial dengan waktu tunda untuk , yaitu
( ), (8) Dengan positif yang merepresentasikan lama waktu tunda. Pada persamaan (8), f adalah fungsi bentuk ke Bentuk persamaan diferensial dengan waktu tunda kontinu, yaitu
∫ , (9) dan persamaan diferensial dengan waktu tunda diskret, yaitu
, (10) untuk , dan .
Persamaan (8) disebut persamaan diferensial dengan waktu tunda berbentuk linear jika f merupakan fungsi linear dan persamaan (8) disebut persamaan diferensial dengan waktu tunda berbentuk taklinear jika f merupakan fungsi taklinear. Persamaan diferensial dengan waktu tunda yang berbentuk taklinear, memerlukan pelinearan agar dapat diselesaikan secara eksplisit. Menggunakan transformasi koordinat berikut.
,
dengan merupakan titik tetap persamaan diferensial waktu tunda taklinear. Diperoleh
̇ , (11) adalah perpindahan jarak sangat kecil dari titik tetap diantara . Menggunakan ekspansi Taylor disekitar titik tetapnya, diperoleh
̇ ,
dengan (
) dan (
)
7 Misalkan matriks ̇ berukuran , maka suatu vektor taknol A di Rn
disebut vektor eigen dari ̇, jika untuk suatu skalar , yang disebut nilai eigen dari ̇, berlaku
̇ (12)
Dengan solusi dan vektor A disebut vektor eigen yang bersesuaian dengan nilai eigen. Untuk mencari nilai eigen dari matriks ̇ yang berukuran , maka persamaan (12) dapat ditulis sebagai berikut.
( ) (13) I adalah matriks identitas, maka persamaan (13) akan memiliki solusi taknol jika dan hanya jika
( ) , (14) dengan merupakan persamaan karakteristik dari ̇(Lakshamanan dan Senthilkumar 2010).
Sharma dan Samanta (2013) menjelaskan secara umum, jika merupakan titik tetap bersifat stabil yang memiliki bagian real nilai eigen negatif dengan akar persamaan karakteristik (14) adalah Analisis kestabilan titik tetap berdasarkan nilai waktu tunda dapat dilakukan dengan memperhatikan kestabilan titik tetap dan kondisi transversalitas, yaitu kondisi yang dapat mengubah sifat kestabilan bila melewati suatu titik kritis pada garis imajiner dan akar persamaan karakteristik (14) akan bergerak menuju bidang imajiner yang positif ketika nilai waktu tunda melebihi titik kritis Kondisi untuk transversalitas adalah sebagai berikut.
karena
.
Dengan demikian, titik tetap memunyai batasan kestabilan menurut waktu tunda sebagai berikut.
1. stabil untuk , 2. tidak stabil untuk , dan
3. mengalami bifurkasi Hopf pada saat .
8
HASIL DAN PEMBAHASAN
Model Matematika
Pal dan Samanta (2010) memodelkan populasi spesies tunggal pada lingkungan tercemar dengan mempertimbangkan keberadaan fungsi kontrol berupa input polutan eksogen pada populasi, kemudian mempertimbangkan adanya efek waktu tunda diskret bagi polutan dalam mencemari lingkungan tercemar. Kemudian, Sharma dan Samanta (2013) dengan menggunakan model dasar yang sama seperti Pal dan Samanta, mempertimbangkan kembali adanya efek waktu tunda tunggal diskret bagi polutan pada lingkungan tercemar dalam mencemari populasi dengan mempertimbangkan keberadaan fungsi kontrol berupa input polutan eksogen dalam lingkungan yang tercemar.
Model Matematika Populasi Spesies Tunggal
pada Lingkungan Tercemar Tanpa Waktu Tunda
Dalam karya ilmiah ini akan dibahas model populasi spesies tunggal pada lingkungan tercemar Sharma dan Samanta (2013), untuk melihat dinamika pertumbuhan populasi spesies tunggal pada lingkungan tercemar. Modelnya sebagai berikut.
Asumsi yang dipakai pada model adalah
A1. Ada polutan yang diberikan pada lingkungan dan organisme hidup, yang kemudian polutan tersebut masuk ke dalam lingkungan dan tubuh organisme hidup tersebut.
A2. Untuk tingkat pertumbuhan populasi, diasumsikan bahwa tingkat kelahiran adalah dan tingkat kematian adalah , dengan
, dan semua parameter positif.
9
Melalui penondimensionalan ini, sistem persamaan (15) dapat dituliskan menjadi
dengan
. (Lampiran 1) Tabel Notasi
Notasi Definisi
n(t) konsentrasi biomassa populasi pada waktu t c(t) konsentrasi polutan pada populasi pada waktu t s(t) konsentrasi polutan pada lingkungan pada waktu t
X merepresentasikan konsentrasi biomassa populasi Y merepresentasikan konsentrasi polutan pada populasi Z merepresentasikan konsentrasi polutan pada lingkungan k tingkat pengurangan polutan pada lingkungan karena
adanya asupan populasidari lingkungantercemar
r tingkat pengurangan polutan di dalam tubuh populasi karena adanya sekresi
m tingkat pengurangan polutan di dalam tubuh populasi karena adanya metabolisme
h tingkat pengurangan polutan pada lingkungan secara alami oleh lingkungan
tingkat pengurangan polutan pada lingkungan karena kaitannya dengan konsentrasi polutan pada populasi
f tingkat pengurangan konsentrasi biomassa populasi karena kompetisi antarspesies
u(t) tingkat input polutan eksogen yang diasumsikan fungsi smooth bounded taknegatif pada waktu t
a
merepresentasikan tingkat pengurangan polutan pada lingkungan karena adanya asupan populasi dari lingkungan tercemar dan tingkat pengurangan konsentrasi biomassa populasi karena kompetisi antarspesies
p tingkat pertumbuhan alami populasi dalam keadaan tidak ada polutan dalam populasi
10
biomassa populasi akibat kompetisi antarspesies
d tingkat pengurangan polutan pada populasi yang berhubungan dengan sekresi dan kematian populasi
merepresentasikan penambahan input polutan eksogen ke dalam lingkungan pada waktu t
Penentuan Titik Tetap Model Populasi Spesies Tunggal
pada Lingkungan Tercemar
Dalam penentuan titik tetap model populasi spesies tunggal pada lingkungan tercemar tanpa waktu tunda, terdapat dua kasus, yaitu kasus pertama merepresentasikan tidak ada penambahan input polutan eksogen ke dalam lingkungan tercemar pada waktu t yang dilambangkan dengan , sehingga mengubah sistem persamaan (16) menjadi Model
kasus kedua merepresentasikan ada penambahan input polutan eksogen ke dalam lingkungan tercemar pada waktu t yang dilambangkan dengan . Selanjutnya kasus kedua ini akan disebut sebagai Model .
Analisis Titik Tetap untuk Model
Titik tetap Model diperoleh dengan menyelesaikan sistem persamaan berikut.
Diperoleh titik tetap .
11
Analisis Kestabilan Titik Tetap untuk Model
Pelinearan Model menghasilkan matriks Jacobi sebagai berikut.
Kestabilan titik tetap dapat dilihat dari nilai eigen yang dihasilkan oleh matriks Jacobi Model yang dievaluasi pada titik tetap tersebut.
Untuk menganalisis kestabilan titik tetap substitusikan ke dalam persamaan matriks Jacobi Model . Diperoleh
(
)
Selanjutnya penyelesaian persamaan karakteristik ( ) menghasilkan nilai eigen untuk matriks , yaitu
Parameter p dan q diasumsikan bernilai positif, sehingga , dan . Dari nilai eigen yang diperoleh, disimpulkan bahwa kestabilan bersifat sadel hiperbolik karena bagian real nilai eigen pertama bernilai positif dan bagian real kedua nilai eigen selanjutnya bernilai negatif serta nilai eigen yang diperoleh merupakan nilai eigen taknol (Meiss 2007).
Untuk menganalisis kestabilan titik tetap Substitusikan ke dalam persamaan matriks Jacobi Model , diperoleh
Selanjutnya, penyelesaian persamaan karakteristik ( ) 0, menghasilkan nilai eigen untuk matriks , yaitu
√
Jika dan , maka bagian real nilai eigen kompleks akan bernilai negatif. Dari nilai eigen yang diperoleh, disimpulkan bahwa kestabilan bersifat stabil asimtotik lokal (Giesl 2007).
12
Analisis Titik Tetap untuk Model
> 0
Diberikan Model sebagai berikut.
Titik tetap Model diperoleh dengan menyelesaikan sistem persamaan berikut.
(20)
Diperoleh titik tetap Model yaitu
dengan
(Lampiran 3)
Analisis Kestabilan Titik Tetap untuk Model
> 0
Untuk menganalisis kestabilan titik tetap
substitusikan ke dalam persamaan matriks Jacobi Model , diperoleh
(
13
Selanjutnya penyelesaian persamaan karakteristik
menghasilkan nilai eigen untuk matriks
, yaitu
Jika , maka komponen nilai eigen akan bernilai positif dan kestabilan titik tetap bersifat tidak stabil, karena tidak semua bagian real nilai eigen bernilai negatif. Sedangkan jika maka komponen nilai eigen akan bernilai negatif dan kestabilan titik tetap bersifat stabil asimtotik lokal, karena semua bagian real nilai eigen bernilai negatif (Giesl 2007).
Untuk menganalisis kestabilan titik tetap Substitusikan ke dalam persamaan matriks Jacobi Model .Diperoleh
Untuk menyederhanakan , dimisalkan
(
)
Selanjutnya, dilakukan penyelesaian terhadap persamaan karakteristik ( ) , yaitu
, dengan
(Lampiran 5) Karena semua parameter diasumsikan positif, jika dan maka menurut kriteria Routh-Hurwitz, sistem bersifat stabil asimtotik lokal (Fisher 1990).
14
, , dan Menggunakan fungsi Lyapunov yang bersifat definit positif pada titik tetap dapat ditentukan batas titik tetap yang harus dipenuhi agar memiliki kestabilan global. Pal dan Samanta (2010) menggunakan fungsi Lyapunov berikut pada model spesies tunggal pada lingkungan tercemar
( )
Turunan dari fungsi Lyapunov terhadap t, diperoleh
dengan
Untuk memenuhi kondisi kestabilan global, turunan dari fungsi Lyapunov terhadap t harus memiliki sifat definit negatif, oleh karena itu
harus memenuhi ,
Titik tetap memiliki kestabilan global jika memenuhi batas berikut.
(Lampiran 6)
Analisis Bifurkasi Hopf untuk Model
> 0
Pada titik tetap bifurkasi Hopf tidak dapat terlihat secara eksplisit dari parameter yang terdapat pada Model . Sehingga diasumsikan adalah salah satu dari semua parameter yang terkait pada Model > 0. Jika nilai parameter terjadi saat bifurkasi Hopf di titik tetap , maka dengan kondisi , Liu (1994) membuktikan bahwa syarat perlu dan cukup agar terjadi bifurkasi Hopf, yaitu
15 Dengan demikian, titik tetap mengalami bifurkasi Hopf pada
Model Matematika Populasi SpesiesTunggal Pada
Lingkungan Tercemar dengan Waktu Tunda Tunggal Diskret
Selanjutnya akan dibahas model populasi spesies tunggal pada lingkungan tercemar dengan waktu tunda tunggal diskret. Model ini menggambarkan pertumbuhan populasi spesies tunggal pada lingkungan tercemar dengan ada penambahan input polutan eksogen ke dalam lingkungan tercemar pada waktu t dan efek penundaan yang membuat model lebih mempertimbangkan realitas. Konsep penundaan ini terjadi karena penyerapan polutan oleh populasi dari lingkungan tercemar tidak seketika terserap oleh populasi, melainkan membutuhkan waktu hingga akhirnya mencemari populasi. Berikut ini adalah sistem persamaan modelnya
dengan nilai awal dan untuk
Semua parameter yang digunakan dalam persamaan (21) sama seperti yang digunakan pada Model kecuali parameter yang merupakan konstanta positif waktu tunda. merepresentasikan waktu yang diperlukan polutan untuk mencemari populasi.
Analisis Titik Tetap dan Kestabilan Model Populasi Spesies
Tunggal pada Lingkungan Tercemar dengan Waktu Tunda
Tunggal Diskret
Titik tetap Model yaitu16
digunakan titik tetap , yang memiliki kestabilan bersifat stabil asimtotik lokal dan global.
Dilakukan transformasi koordinat pada sistem (21) agar sistem tetap berpusat pada kesetimbangan titik tetap Transformasi koordinat yang dilakukan sebagai berikut.
dengan u(t), v(t), dan w(t) adalah perpindahan jarak titik tetap sangat kecil dari titik tetap yang berada diantara .
Selanjutnya dilakukan pelinearan terhadap sistem persamaan (21). Dihasilkan dua matriks Jacobi sebagai berikut.
(
)
17 Penggunaan ekspansi Taylor, pada pelinearan sistem persamaan (21) diperoleh
( ) ( ) (Lampiran 7) Selanjutnya, diasumsikan solusi sistem persamaan yang menggambarkan perpindahan jarak sangat kecil karena adanya penundaan. Solusi sistem ini adalah fungsi eksponensial seperti pada persamaan diferensial biasa, yaitu
dengan ( ) , diperoleh persamaan karakteristik
, (22) dimana (23) (Lampiran 8)
Analisis Bifurkasi Hopf Model dengan Waktu Tunda Tunggal
Diskret
Asumsikan persamaan karakteristik (22) memiliki solusi imajiner murni berbentuk . Dengan dipertimbangkan adanya bifurkasi Hopf pada titik tetap . Kemungkinan adanya perubahan kestabilan pada dapat terjadi karena adanya perubahan nilai parameter sehingga terjadi perubahan kestabilan bersifat stabil jika dan bersifat tidak stabil jika . Oleh karena itu digunakan nilai eigen dengan dalam melakukan analisis adanya bifurkasi Hopf.
Substitusikan nilai eigen pada persamaan (22) dan pisahkan antara bagian real dan bagian imajiner, diperoleh
(24)
Eliminasi dengan menguadratkan dan menjumlahkan persamaan bagian real dan bagian imajiner, diperoleh
18 dimana
Misalkan , diperoleh
(26) Klaim 1
Untuk , maka persamaan (26) tidak memiliki akar positif.
selanjutnya
, atau
, (27)
kemudian, diperoleh
√
Jika maka sehingga ( ) Hal ini menunjukkan bahwa tidak ada satupun dari yang bernilai positif dan menunjukkan bahwa persamaan (26) tidak memiliki akar yang positif. Sehingga tidak ada sedemikian sehingga membuat nilai eigen dari persamaan (26) adalah positif. Oleh karena itu, hanya mungkin jika setiap bagian real nilai eigen persamaan (22) negatif ketika waktu tunda Titik tetap memenuhi
pada kriteria Routh-Hurwitz persamaan (22) (Fisher 1990) dan memenuhi yang memiliki bagian real nilai eigen negatif pada waktu tunda dan titik tetap pada persamaan diferensial dengan waktu tunda memiliki kestabilan bersifat stabil asimtotik lokal ketika waktu tunda .
Klaim 2
Untuk maka sehingga persamaan (26) memiliki setidaknya satu akar positif.
Jika maka ( ) dan ( )
sehingga persamaan (25) memiliki akar positif pada solusi berbentuk akar imajiner . Dari persamaan (24), diperoleh
19 ketika , maka persamaan (22) akan memiliki akar berbentuk imajiner dengan kondisi sebagai berikut.
dan .
Untuk mengetahui kurva berada pada keadaan stabil, dilakukan identifikasi kondisi tranversalitas sebagai berikut.
( )
Dari persamaan (22), diperoleh
( ) dan
( ) (Lampiran 9) Substitusikan pada persamaan (29), maka diperoleh bagian real dan bagian imajiner sebagai berikut.
( )
( )
Jika adalah akar positif dari persamaan (26), maka yang merupakan akar dari persamaan (25) adalah akar positif, sehingga kondisi tranversalitas terpenuhi, yaitu
karena
20
Kondisi ini menunjukkan bahwa terjadi kondisi tidak stabil ketika , sehingga terjadi bifurkasi Hopf pada titik kritis , yang merupakan nilai positif terkecil dari
Titik tetap memenuhi pada kriteria Routh-Hurwitz persamaan (22) (Fisher 1990) dan memenuhi dan kondisi tranversalitas
sehingga titik tetap pada persamaan diferensial dengan waktu tunda memiliki kestabilan bersifat tidak stabil ketika waktu tunda (Sharma dan Samanta 2013).
Menggunakan Klaim 1 dan Klaim 2, titik tetap memenuhi pada kriteria Routh-Hurwitz (Fisher 1990) dan memenuhi kemudian memenuhi dan kondisi tranversalitas
sehingga titik tetap pada persamaan diferensial dengan waktu tunda memiliki kestabilan bersifat stabil asimtotik lokal ketika waktu tunda dan bersifat tidak stabil ketika waktu tunda (Sharma dan Samanta 2013).Dengan
Titik tetap menunjukkan adanya bifurkasi Hopf pada , merupakan nilai parameter yang membuat titik tetap mengalami bifurkasi Hopf (Sharma dan Samanta 2013).
Perkiraan Panjang Waktu Tunda
Mempertimbangkan bahwa sistem persamaan diferensial Model dan setiap nilai real merupakan fungsi kontinu yang didefinisikan pada [– ] dari suatu kondisi awal [– ]. Dapat dilakukan perkiraan panjang waktu tunda untuk mempertahankan kestabilan suatu sistem.
Pelinearan sistem persamaan dengan waktu tunda tunggal diskret pada titik tetap diperoleh
21
dengan,
Transformasikan persamaan (30) menggunakan transformasi Laplace, diperoleh
̅ ̅ ̅ ̅ ̅ (31) ̅ ̅ ̅
dengan ∫ dan ̅ ̅ ̅ adalah hasil transformasi Laplace dari
Gunakan persamaan (31) dan persamaan (23), diperoleh ̅
̅
(Lampiran 10) Invers transformasi Laplace dari ̅ akan memunyai terminologi eksponensial yang meningkat terhadap waktu, jika ̅ memiliki kutub dengan bagian real positif. Titik tetap stabil asimtotik lokal jika memenuhi syarat cukup dan perlu untuk setiap kutub dari ̅ yaitu memiliki bagian real negatif (Erbe et al. 1986).
Kriteria Nyquist merupakan kriteria penguat kestabilan yang fokus pada pemaksimuman nilai frekuensi dari akar persamaan karakteristik berbentuk imajiner murni (Nyquist 1932).
(Erbe et al. 1986) menjelaskan kriteria Nyquist. Jika adalah panjang busur lingkaran sepanjang suatu kurva yang melingkari separuh lingkaran pada bagian kanan, kemudian kurva ̅ akan mengelilingi nilai awalsebanyak selisih banyaknya kutub dan banyaknya nol pada kurva separuh lingkaran bagian kanan, maka dapat ditunjukkan titik tetap memiliki stabil asimtotik lokal bila memenuhi kondisi berikut.
dengan .
22
dengan adalah nilai waktu tunda paling kecil dimana ada suatu solusi bagian real bernilai nol (Freedman dan Rao 1983).
Menggunakan persamaan (32), persamaan (33), dan persamaan (24), diperoleh (34) (35) Menggunakan persamaan (34) dan persamaan (35), diperoleh
[| | √| | | | ], (36) Dengan Dan
√ (37) dengan
| |
jadi, kestabilan sistem terjadi ketika , dengan merupakan waktu maksimum bagi sistem bersifat stabil asimtotik lokal.
(Lampiran 10)
SIMULASI MODEL TANPA WAKTU TUNDA
Dinamika populasi spesies tunggal pada lingkungan tercemar untuk kurun waktu tertentu dapat ditunjukkan melalui kurva bidang solusi dan bidang fase. Proses komputasi untuk menghasilkan kurva bidang solusi dan bidang fase ini menggunakan bantuan software matematika dengan terlebih dahulu memberikan nilai untuk parameter dan nilai awal untuk masing-masing variabel.
Asumsikan bahwa tingkat kematian populasi spesies tunggal pada lingkungan tercemar adalah positif atau agar tidak terjadi kepunahan pada populasi. Asumsi ini memberikan syarat yang berarti bahwa tingkat pertumbuhan populasi spesies tunggal pada kondisi populasi tidak terkena polutan harus positif. Dengan demikian, batas konsentrasi polutan yang terdapat pada populasi pada waktu t adalah . Dalam simulasi ini, asumsi tersebut harus dipenuhi oleh setiap titik tetap. Khusus untuk titik tetap
nilai-nilai parameter yang digunakan harus terlebih dahulu memenuhi dua kondisi parameter batas keberadaan titik tetap
23 penambahan input polutan eksogen ke dalam lingkungan tercemar untuk memperoleh kestabilan bersifat stabil asimtotik lokal. Kondisi merepresentasikan bahwa tingkat pengurangan polutan pada lingkungan tercemar harus lebih besar daripada penambahan input polutan eksogen ke dalam lingkungan tercemar untuk memperoleh kestabilan bersifat tidak stabil.
Selanjutnya, untuk titik tetap nilai-nilai parameter yang digunakan harus terlebih dahulu memenuhi dua kondisi parameter batas keberadaan titik tetap yaitu dan Kondisi merepresentasikan bahwa kemampuan populasi mengurangi polutan yang berasal dari lingkungan tercemar harus lebih besar daripada pengurangan polutan secara alami oleh alam. Representasi kondisi untuk titik tetap
sama seperti kondisi untuk
.
Tabel 1 Nilai parameter yang digunakan pada pada Model dan Model dengan
Parameter Nilai
p 2.28
q 2.92
a 4.14
d 0.54
h 0.2
Tabel 2 Nilai parameter yang digunakan Model dan
Parameter Nilai
p 2.28
q 2.92
a 4.14
d 0.54
h 0.1
Dinamika Populasi Spesies Tunggal untuk Model
24
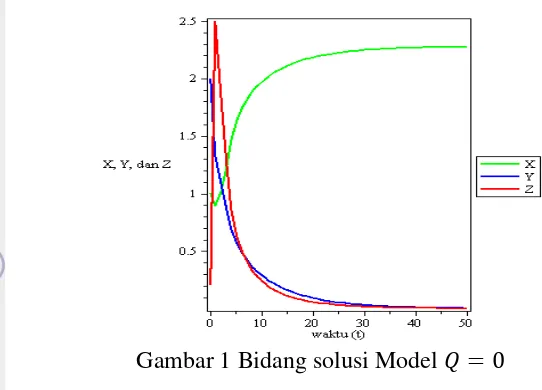
Gambar 1 Bidang solusi Model
Gambar 1 menunjukkan dinamika Model yaitu kondisi model ketika tidak ada penambahan input polutan eksogen ke dalam lingkungan tercemar. Pada model ini, konsentrasi polutan pada lingkungan dan populasi menurun. Pengurangan ini dapat mempertahankan keberadaan populasi pada lingkungan tercemar yang ditandai dengan meningkatnya konsentrasi biomassa populasi.
Dinamika Populasi Spesies Tunggal untuk Model
> 0 dengan
<
[image:36.595.90.415.468.687.2]Untuk mengamati dinamika model ini pada bidang solusi, digunakan nilai parameter pada Tabel 2 dengan = 1.25 serta nilai awal X(0) = 1, Y(0) = 1, dan Z(0) = 5. Dihasilkan titik tetap ,4 28 ,12 5 dengan nilai eigen -2 92 - 1 dan -2 sehingga titik tetap adalah stabil asimtotik lokal.
Gambar 2 Bidang solusi pada Model dan
25 ini, terjadi peningkatan konsentrasi polutan pada lingkungan dan populasi. Peningkatan tersebut mengakibatkan konsentrasi biomassa populasi relatif rendah. Hal ini menggambarkan bahwa keberadaan populasi pada lingkungan tercemar terancam punah.
Dinamika Populasi Spesies Tunggal untuk Model
> 0 dengan
>
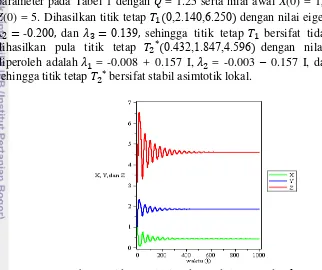
[image:37.595.117.439.234.504.2]Untuk mengamati dinamika model ini pada bidang solusi, digunakan nilai parameter pada Tabel 1 dengan = 1.25 serta nilai awal X(0) = 1, Y(0) = 1, dan Z(0) = 5. Dihasilkan titik tetap ,2 14 ,6 25 dengan nilai eigen -2 92 , - 2 dan 139 sehingga titik tetap bersifat tidak stabil. Dan dihasilkan pula titik tetap 432,1 847,4 596 dengan nilai eigen yang diperoleh adalah = -0.008 + 0.157 I, = -0.003 – 0.157 I, dan - 893 sehingga titik tetap bersifat stabil asimtotik lokal.
Gambar 3 Bidang solusi pada Model dan
Gambar 3 menunjukkan dinamika Model > 0 dan yaitu kondisi ketika ada penambahan input polutan eksogen ke dalam lingkungan tercemar dan pengurangan polutan pada lingkungan tercemar lebih besar daripada penambahan input polutan eksogen ke dalam lingkungan tercemar. Pada model ini, terjadi perubahan kestabilan yang ditandai dengan adanya osilasi kemudian menuju titik tetap 432,1 847,4 596 .
Kestabilan Global pada Titik Tetap
26
Gambar 4 Bidang fase yang menunjukkan kestabilan global
Gambar 4 menunjukkan untuk semua titik awal akan bergerak menuju satu titik tetap yang sama, yaitu titik tetap 432,1 847,4 596 yang berbentuk spiral.
Titik tetap merupakan titik tetap yang memiliki kestabilan yang tetap, yaitu selalu bersifat tidak stabil dan bersifat stabil asimtotik lokal. Sedangkan titik tetap merupakan titik tetap yang dapat berubah sesuai dengan perubahan nilai parametertingkat pengurangan polutan pada tubuh populasi melalui sekresi, metabolisme, atau pengurangan polutan lainnya (q), nilai parameter tingkat pertumbuhan alami populasi dalam keadaan tidak ada polutan dalam populasi (p), dan nilai parameter penambahan polutan eksogen ke dalam lingkungan tercemar ( ). Pada simulasi karya ilmiah ini akan dibahas perubahan kestabilan titik tetap dan .
Dinamika Populasi Spesies Tunggal pada Lingkungan Tercemar
Berdasarkan Parameter
q
Tabel 4 Pengaruh perubahan nilai parameter q terhadap bifurkasi Hopf
No q Kestabilan Titik Tetap
.
1 < 2.90 Tidak stabil Stabil asimtotik lokal
2 2.90-2.91 Tidak stabil Tidak stabil
27
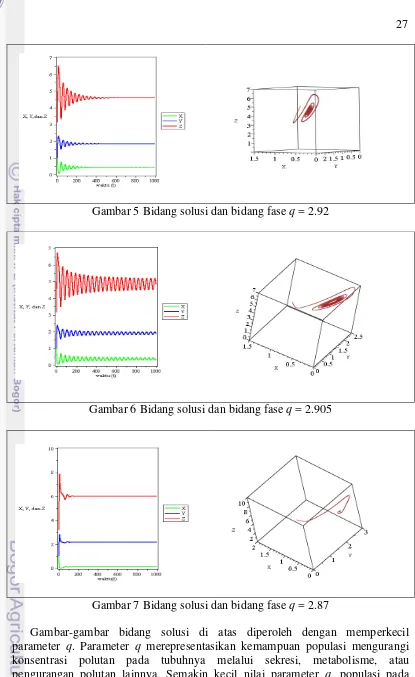
Gambar 5 Bidang solusi dan bidang fase q = 2.92
Gambar 6 Bidang solusi dan bidang fase q = 2.905
Gambar 7 Bidang solusi dan bidang fase q = 2.87
28
biomassa populasi relatif rendah. Selanjutnya, pada gambar-gambar bidang fase di atas terdapat kemunculan limit cycle akibat adanya bifurkasi Hopf.
[image:40.595.69.490.161.770.2]Dinamika Populasi Spesies Tunggal pada Lingkungan Tercemar
Berdasarkan Parameter
p
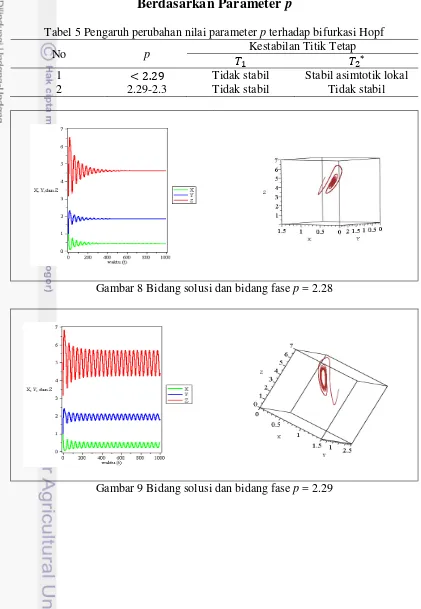
Tabel 5 Pengaruh perubahan nilai parameter p terhadap bifurkasi Hopf
No p Kestabilan Titik Tetap
1 Tidak stabil Stabil asimtotik lokal
2 2.29-2.3 Tidak stabil Tidak stabil
Gambar 8 Bidang solusi dan bidang fase p = 2.28
29
[image:41.595.112.517.55.264.2]Gambar 10 Bidang solusi dan bidang fase p = 2.3
Gambar-gambar bidang solusi di atas diperoleh dengan memperbesar parameter p. Parameter p menggambarkan tingkat pertumbuhan alami populasi dengan kondisi populasi bebas daripengaruh polutan. Parameter p yang semakin besar mengakibatkan ketidakstabilan pada sistem yang ditandai dengan adanya osilasi dan peningkatan konsentrasi polutan pada lingkungan. Kondisi ini dapat mengancam keberadaan populasi pada lingkungan tercemar. Selanjutnya pada gambar-gambar bidang fase di atas terdapat kemunculan limit cycle akibat adanya bifurkasi Hopf.
[image:41.595.107.519.423.762.2]Dinamika Populasi Spesies Tunggal pada Lingkungan Tercemar
Berdasarkan Parameter
Tabel 6 Pengaruh perubahan nilai parameter terhadap bifurkasi Hopf
No Kestabilan Titik tetap
1 Tidak stabil Stabil asimtotik lokal
2 1.270-1.291 Tidak stabil Tidak stabil
3 1.291 Tidak stabil Stabil asimtotik lokal
4 >1.33 Stabil asimtotik lokal Tidak berlaku
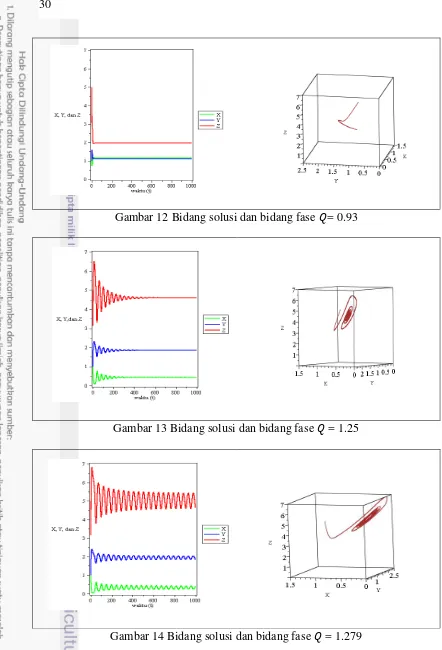
30
Gambar 12 Bidang solusi dan bidang fase = 0.93
Gambar 13 Bidang solusi dan bidang fase = 1.25
31
Gambar 15 Bidang solusi dan bidang fase = 1.298
Gambar 16 Bidang solusi dan bidang = 1.33
32
Gambar-gambar bidang solusi di atas diperoleh dengan mengubah parameter menjadi lebih besar. Parameter merepresentasikan penambahan input polutan eksogen ke dalam lingkungan tercemar. Memperbesar parameter mengakibatkan konsentrasi biomassa populasi relatif rendah, tetapi konsentrasi polutan pada lingkungan dan populasi relatif tinggi. Hal ini menggambarkan populasi terancam punah pada lingkungan tercemar. Selanjutnya pada gambar-gambar bidang fase di atas terdapat kemunculan limit cycle akibat terjadi bifurkasi Hopf.
DINAMIKA MODEL DENGAN WAKTU TUNDA
Pada bagian ini akan dibahas dinamika populasi spesies tunggal dalam lingkungan tercemar yang mempertimbangkan efek waktu tunda. Parameter waktu tunda yang akan digunakan adalah
dan
, dengan
dan
[image:44.595.85.455.317.603.2]
diperoleh 0.025, 0.160, dan 0.021. Selanjutnya terjadi perubahan kestabilan pada titik tetap 432,1 847,4 596 karena perubahan nilai parameter .
Tabel 7 Perubahan kestabilan titik tetap 432,1 847,4 596 berdasarkan nilai parameter
Titik tetap Kondisi Kestabilan
33 Selanjutnya, menggunakan kriteria Nyquist, nilai frekuensi dimaksimumkan untuk mendapatkan nilai waktu tunda maksimum. Penggunaan kriteria ini dimaksudkan untuk mempertahankan kestabilan model dengan waktu tunda. Nilai frekuensi dan nilai waktu tunda maksimum yang akan digunakan adalah
| | √| | | |
√ dengan
| |
diperoleh nilai 2.217 dan 0.672. Sehingga kestabilan titik tetap 432,1 847,4 596 dapat dipertahankan jika kondisi waktu tunda yang diberikan pada interval (0, ).
Tabel 8 Perubahan kestabilan titik tetap 432,1 847,4 596 berdasarkan nilai parameter
Titik tetap Kondisi Kestabilan
432,1 847,4 596 Stabil asimtotik lokal Tidak stabil Muncul bifurkasi Hopf Adanya perubahan kestabilan akibat perubahan parameter yang terjadi pada titik tetap 432,1 847,4 596 dapat dijadikan indikasi munculnya bifurkasi. Akan tetapi, kemunculan bifurkasi Hopf yang dapat dilihat melalui kemunculan limit cycle masih sulit dibuktikan dalam bidang fase karena keterbatasan penulis dalam menggunakan software matematika lain yang lebih mumpuni dalam menganalisis sistem persamaan diferensial dengan waktu tunda dimensi tiga.
SIMPULAN
34
sehingga polutan pada lingkungan meningkat dan populasi pada lingkungan tersebut terancam punah. Semakin besar penambahan polutan eksogen ke dalam lingkungan tercemar, semakin mengancam keberadaan populasi pada lingkungan tercemar semakin terancam punah. Dengan demikian, kondisi yang mampu mempertahankan keberadaan populasi pada lingkungan tercemar adalah peningkatan dalam hal kemampuan populasi mengurangi polutan yang ada dalam tubuhnya, penurunan tingkat pertumbuhan alami populasi dan pengurangan input polutan eksogen yang diberikan pada lingkungan tercemar.
Selain pengaruh di atas, dinamika populasi spesies tunggal dalam lingkungan tercemar juga dapat dipengaruhi oleh parameter waktu tunda . Adanya efek waktu tunda membuat model mempertimbangkan realitas. Realitas yang dimaksudkan adalah penyerapan polutan oleh populasi dari lingkungan tercemar tidak seketika terserap oleh populasi, melainkan membutuhkan waktu hingga akhirnya mencemari populasi. Dengan mengubah nilai-nilai parameter, dinamika populasi akantidak stabil. Akan tetapi, melalui pendugaan panjang waktu tunda didapatkan nilai waktu tunda maksimum. Oleh sebab itu, kestabilan dinamika populasi terjadi pada selang waktu tunda .
DAFTAR PUSTAKA
Erbe LH, Freedman HI, Rao VSH. 1986. Three Species Food Chain Models with Mutual Interference and Time Delays. Mathematical Biossciences. 80(1):57-80.
Fisher SD. 1990. Complex Variables Second Edition. California (US): Wadsworth & Brooks/Cole Brooks & Software, Pacific Grove.
Freedman HI, Rao VSH. 1983. The Trade Off Between Mutual Interference and Time Lags in Predator Prey Systems. Bulletin of Mathematical Biology. 45, (6):991–1004.
Giesl P. 2007.Construction of Global Lyapunov Functions Using Radial Basis Functions. Hiedelberg (DE): Springer-Verlag.
Hallam GP, Clark CE, Lassiter RR.1983. Effects of Toxicants on Populations: A Qualitative Approach. 1. Equilibrium Environmental Exposure. Ecological Modelling. 18(4): 291–304.
Kuang Y. 1993. Delay Differential Equation with Application in Population Dynamics. Boston:Academic Press.
Lakshmanan M,Senthilkumar DV. 2010. Dynamics of Nonlinear Time-Delay
Systems. Hiedelberg (DE): Springer-Verlag.
L o ’ VD 2 9 o r c o of L p ov F c o for c SIS, SIR and SIRS Epidemic Model with Variable Population Size, Mat-Red Foro, Vol. 26, www.red-mat.unam.mx/foro/volumenes/Vol026.
Liu WM. 1994. Criterion of Hopf Bifurcations without Using Eigenvalues.Journal of Mathematical Analysis and Applications. 182(1): 250–256.
35 Nyquist H. 1932. Regeneration Theory.Bell System Technical Journal.
11:126-147.
Pal AK, Samanta GP. 2010. Dynamics Model of A Single Species System in A Polluted Environment. Journal of Applied Mathematics & Computing. 16(1-2): 231-242.
Sharma S, Samanta GP. 2013. Mathematical Analysis of A Single Species Population Model in A Polluted Environment with Discrete Time Delays.Journal of Mathematics.574213:18 doi:10.1155/2013/574213. Siahaan NHT. 2004. Hukum Lingkungan dan Ekologi Pembangunan Edisi Kedua.
Herman Sinaga, Yati Sumiharti, editor. Jakarta(ID): Erlangga.
Strogatz SH. 1994. Nonlinear Dynamics and Chaos, with Application to Physics, Biology, Chemistry, and Engineering. New York (US): Addison-Wesley Publishing Company.
TuPNV. 1994. Dynamic System: An Introduction with Application in Economics and Biology. Hiedelberg (DE): Springer-Verlag.
Van Lier, Irene H. 1980. Acid Rain and The International Law. Bunsel Environmental Consultant. Toronto.
36
Lampiran 1 Penondimensionalan Model
Dilakukan penondimensionalan persamaan (16) dengan skala parameter yang digunakan, yaitu
( ( ) ( ))
( ) ( ( ))
( )
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
(
) (
)
Misalkan
37
Lampiran 2 Penentuan Titik Tetap untuk Model
Titik tetap Model diperoleh dengan menyelesaikan sistem persamaan (19)
Substitusikan persamaan (41) ke persamaan (42) dan (43), diperoleh dan Sehingga titik tetap
Dari persamaan (42) dan (43). Jika diperoleh nilai maka pastilah nilai , sehingga dengan mensubstitusikan nilai Z dan Y ke persamaan (41) diperoleh Sehingga diperoleh titik tetap
Lampiran 3 Penentuan Titik Tetap untuk Model > 0
Titik tetap Model diperoleh seperti penyelesaian pada persamaan (41), dan (42), kecuali pada persamaan (43)
Substitusikan persamaan (41) dan (44) ke persamaan (41), diperoleh sehingga titik tetap
Eliminasi pada persamaan (21), menghasilkan
38
Sederhanakan persamaan (46), diperoleh
( )
Misalkan
√
maka diperoleh
( )
( )
Substitusikan persamaan (47) ke persamaan (41), diperoleh
39
( )
Dihasilkan titik tetap
Lampiran 4 Penentuan Nilai Eigen untuk Model Misalkan Model dituliskan sebagai berikut.
Dengan melakukan pelinearan diperoleh matriks Jacobi sebagai berikut.
40
Pelinearan Titik Tetap
Substitusikan titik tetap ke dalam matriks Jacobi Model dengan pendekatan limit
,
(
) .
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik ( ) , sehingga diperoleh
| |
|
|
Pelinearan Titik Tetap
Substitusikan titik tetap ke dalam matriks Jacobi Model
,
(
41
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik ( ) , sehingga diperoleh
| |
|
|
( )
√
Lampiran 5 Penentuan Nilai Eigen untuk Model > 0 Misalkan Model dituliskan sebagai berikut.
Dengan melakukan pelinearan diperoleh matriks Jacobi sebagai berikut.
(
)
( )
( )
42
Pelinearan Titik Tetap
Substitusikan titik tetap ke dalam matriks Jacobi Model
,
(
)
.
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik
, sehingga diperoleh |
43
|
| ( )
| |
(( ) )
Pelinearan Titik Tetap
Substitusikan titik tetap ke dalam matriks Jacobi Model
,
, misalkan
(
).
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik ( ) , sehingga diperoleh
| |
|
|
44
diperoleh
Lampiran 6 Kestabilan global
( )
Turunan dari fungsi Lyapunov terhadap t, diperoleh
dengan
Lampiran 7 Pelinearan Model Dengan Waktu Tunda
Misalkan model dengan waktu tunda dituliskan sebagai berikut.
45
(
)
( )
( )
( )
46 ( ) ( ) ( ) ( ) ( )
Substitusikan titik tetap ke dalam matriks Jacobi , diperoleh
47 ( )
Substitusikan titik tetap ke dalam matriks Jacobi , diperoleh
( ) misalkan ( )
Sesuai dengan deret Taylor ̇ , dengan (
) dan (
) merupakan matriks Jacobi x yang
dievaluasi pada titik tetapnya dan merupakan matriks Jacobi yang dievaluasi pada titik tetapnya (Lakshamanan dan Senthilkumar 2010).
Pelinearan model dengan waktu tunda diperoleh
( ) ( )
Lampiran 8 Mencari persamaan karakteristik model dengan waktu tunda
48
( )
misalkan
.
Lampiran 9 Analisis bifurkasi Hopf model dengan waktu tunda
Asumsikan persamaan karakteristik (22) memiliki solusi imajiner murni berbentuk . Substitusikan nilai eigen pada persamaan (22) dan pisahkan bagian real dan imajiner dari persamaan yang diperoleh
disederhanakan menjadi persamaan (24).
Kuadratkan persamaan (24) dan gunakan metode eliminasi, diperoleh
( )
( ) , disederhanakan menjadi persamaan (25).
Gunakan persamaan (24) dalam memperoleh nilai
49
Perubahan kestabilan titik tetap berdasarkan nilai dapat dilakukan menggunakan kondisi tranversalitas, yaitu dengan mendiferensialkan persamaan karakteristik (22) terhadap , sehingga diperoleh
( )
( )
( )
Substitusikan pada persamaan (29), maka diperoleh bagian real dan bagian imajiner.
Lampiran 10 Transformasi Laplace pada model dengan waktu tunda Gunakan transformasi Laplace berikut.
( ) ̅ ∫ dan
( )
50
[ ] ∫
∫
∫
Transformasikan sistem persamaan (30)
̅ ̅ ̅
̅ ̅
̅ ̅ ̅ ∫
̅ ̅ ̅ ∫
∫
̅ ̅ ̅ ∫
∫
̅ ̅ ̅ ∫
∫
̅ ̅ ̅ ∫ ̅
̅ ̅ ̅ ∫
51 ̅ ̅ ̅
̅ ̅ ̅ ̅
̅ ̅ ̅
Transformasi persamaan (30) menggunakan transformasi Laplace, menghasilkan persamaan (31).
Susun ulang persamaan (31)
̅ ̅ ̅
̅ ̅ ̅
̅ ̅ ̅
̅ ̅ ̅ ̅
̅ ̅ ̅ ̅
̅ ̅ ̅
̅
, kemudian, diperoleh
̅
̅ (0) .
Lampiran 11 Kriteria Nyquist
Titik tetap memiliki sifat stabil asimtotik lokal bila memenuhi kondisi (32) dan (33).
Menggunakan persamaan (32) dan persamaan (24), diperoleh persamaan (34) dan (35).
Menggunakan persamaan (34) akan ditentukan menggunakan , dengan adalah batas paling atas dari . Mempertimbangkan , sedemikian sehingga memenuhi , dimana .
52
.
Memaksimumkan nilai dengan | | dan | |
| | | | , dihasilkan persamaan (36)
Menggunakan persamaan (34), diperoleh persamaan (52)
Menggunakan persamaan (35) dan persamaan (52)
artinya
dengan memanipulasi didapatkan
+
menggunakan bagian kiri dari persamaan yang diperoleh persamaan (35) dan persamaan (52), diperoleh
| |
dengan | |
| | | | (i) Dengan | |
( ) | |
53 | | (ii) Diperoleh
| | | |
Sehingga dihasilkan persamaan (37).
Lampiran 12 Kode program bidang solusi
atau
1
54
55
Riwayat Hidup
Penulis dilahirkan di serang pada tanggal 13 Maret 1992, anak kedua dari tiga bersaudara, anak dari Bapak Winardi dan Ibu Masyitoh.
Tahun 2010 Penulis lulus dari SMAN 2 Krakatau Steel dan melanjutkan pendidikan di jurursan Matematika, fakultas Matematika dan Ilmu Pengetahuan Alam (MIPA), Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB (USMI).