Gerak Melingkar dan Gerak Parabola GuruPintar MODUL 1 GM DAN GP
Teks penuh
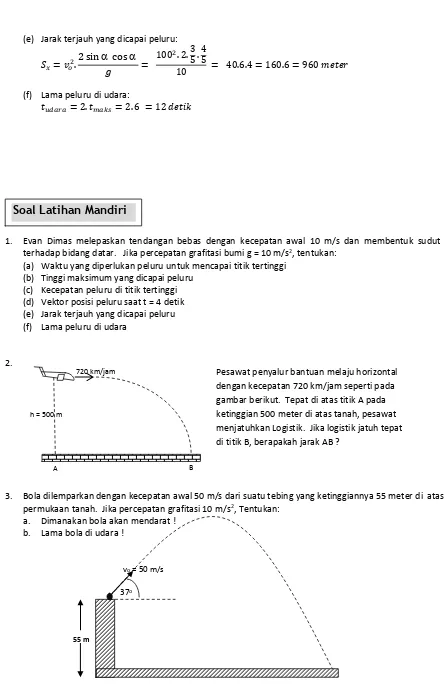
Gambar
Dokumen terkait
Puji syukur Alhamdulillah Allah SWT yang telah melimpahkan rahmat dan karunia-Nya penulis dapat menyelesaikan Karya Tulis Ilmiah ini yang berjudul“Gambaran Pengetahuan
Pada perikanan tangkap, tidak ada produksi yang digunakan untuk bibit/benih, sehingga untuk melihat ketersediaan pangan ikan dari perikanan tangkap Provinsi Jambi
PEMERINTAH KABUPATEN OGAN ILIR. DINAS PENDIDIKAI\ DAN
X adalah koordinat foto yang dikoreksi sepanjang sumbu x untuk titik a, y adalah koordinat foto yang dikoreksi sepanjang sumbu y untuk titik a, xc adalah jarak fiducial
-- Melaksanakan rujukan penderita yang tidak Melaksanakan rujukan penderita yang tidak dapat ditangani (jangan beri salep mata, agar dapat ditangani (jangan beri salep mata, agar
Kabupaten Rokan Hulu dan Kuantan Singingi merupakan kabupaten yang harus mendapatkan prioritas pertama dalam penanggulangan kemiskinan yang dilakukan melalui intervensi
Globalisasi sebenarnya tidak semata-mata berorientasi pada satu pihak- katakanlah sains Barat – namun lebih ideal bersifat dua belah pihak yakni disampi ada