PIRAMIDA PASCAL: SUATU PENGEMBANGAN SEGITIGA PASCAL

PIRAMIDA PASCAL: SUATU PENGEMBANGAN SEGITIGA PASCAL

I Wayan Puja Astawa

SMKN 1 Abang, Kab. Karangasem, Bali

Abstract. The ability to expand and generalize is one of the most important facilities a teacher can help a student develop. In this articles, the familiar application of Pascal’s triangle to determine the coefficients of a binomial expansion ( + ) is develoved by the use of “Pascal’s pyramid” to consider the coefficients of a trinomial expansion (a + b + c)n_{, kwartonomial expansion (a + b + c + d)}n_{, untill polinomial} expansion. Whereas a binomial expansion can be represented by a readily visible triangle, trinomial expansion, kwartonomial expansion until polinomial expansion are represented by the more complex pyramid. There is a unique relationships between Pascal’s triangle and Pascal’s pyramid. The general formula of (a + b)n _called binomial theorem also could be used to determine the formula of trinomial expansion, kwartonomial expansion, until polinomial expansion.

Keyword. binomial’s teorem, kwartonomial, pascal's triangle, pascal's pyramid,

polynomial, trinomial,

1. Pendahuluan

Pada tahun 1963 Blaise Pascal menerbitkan buku yang berjudul

Traité du Triangle Arithmétique dan di

dalamnya terdapat susunan bilangan

yang kemudian dikenal dengan

segitiga Pascal. Meski dikenal dengan nama Pascal, ternyata segitiga Pascal telah dikenal di Cina sebelum tahun 1300 seperti oleh Al-Karaji (953 – 1029), Omar Khayyam (1048 – 1131), Jia Xian (1010 – 1070) dan Ying Hui (1238 – 1290).

Segitiga Pascal merupakan

koefisien-koefisien binomial atau bentuk

aljabar bersuku dua yang tersusun dalam bentuk segitiga. Koefisien

binomial dapat dinyatakan dengan menggunakan kombinasi dan aljabar.

Dengan kombinasi, koefisien

binomial dilambangkan dengan n_r . Bentuk n_r menyatakan banyak cara membuat himpunan bagian dengan r elemen dari suatu himpunan dengan n elemen. Secara aljabar, koefisien binomial merupakan koefisien suku a b pada ekspansi bentuk aljabar dua suku (a + b) untuk n bilangan cacah. Dimulai dengan 1. Setiap baris berikutnya mulai dan berakhir dengan 1. Bilangan lainnya diperoleh dengan menambahkan dua suku terdekat dari baris di atasnya.

(a + b)0 (a + b)1 (a + b)2 (a + b)3 (a + b)4 …       0 0       0 1       1 1       0 2       1 2       2 2       0 3       1 3       2 3       3 3       0 4       1 4       2 4       3 4       4 4

…

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

…

Sebagai contoh, untuk menentukan (a + b) gunakan koefesien-koefesien pada baris ke-5 sehingga:

(a + b) = 4 0 a + 4 1 a b + 4 2 a b + 4 3 ab + 4 4 b atau (a + b) = 1a + 4a b + 6a b + 4ab + 1b .

Dengan menggunakan notasi sigma, ekspansi binomial (a + b) dapat dituliskan dalam bentuk:

)

1

(

...

b

a

r

n

)

b

a

(

n n r r 0 r n  



_















dimana a, b bilangan real, n bilangan cacah dan n_r koefesien binomial dari suku ke-r + 1.

Dalam pembelajaran matematika,

kemampuan untuk menjabarkan dan membuat generalisasi sangat penting bagi guru dalam membantu siswa

mengembangkan kemampuan

matematik. Penerapan segitiga Pascal untuk menentukan ekspansi (a + b) sudah dipelajari sejak pendidikan menengah.

Yang menjadi pertanyaan adalah

bagaimana kalau suku bentuk

aljabar tersebut ditambah? Misalnya (a + b + c)n_{, (a + b + c + d)}n_{, dan} seterusnya sampai bentuk aljabar n buah suku. Dalam konteks ini, segitiga Pascal masih bisa digunakan walaupun harus melalui beberapa tahapan operasi aljabar. Oleh karena itu, pada artikel ini akan diselidiki

susunan koefesien-koefesien dan

rumus dari ekspansi trinomial (a + b + c)n_.

2. Metoda Penulisan

Artikel ini merupakan hasil kajian

pustaka/hasil pemikiran dalam

upaya untuk menggali dan

mengembangkan pengetahuan

matematika yang sudah ada. Hasil pengembangan ini diharapkan dapat

memperkaya teori/materi

matematika, yang nantinya dapat

digunakan untuk memecahkan

masalah yang muncul baik dalam matematika maupun dalam ilmu

lainnya yang memerlukan bantuan matematika.

3. Hasil dan Pembahasan

a. Piramida Pascal

Segitiga pascal merupakan susunan bilangan-bilangan yang merupakan

koefesien-koefesien binomial dari

ekspansi dua suku, misalnya suku-sukunya a dan b. Bagaimana jika terdiri dari 3 suku yaitu a, b dan c atau (a + b + c)n_{. Untuk itu akan} dicoba menguraikan (a + b + c)n

untuk pangkat n kecil dengan

menggunakan formula segitiga

pascal, sebagai berikut.

Untuk n = 0, 1, 2, 3 dan 4 berturut-turut diperoleh (a + b + c)0 _{= 1, (a + b} + c)1 _{= a + b + c, (a + b + c)}2 _{= 1a}2 ₊ 2ab + 2ac + 1b2 _{+ 2bc + 1c}2_{, (a + b +} c)3 _{= 1a}3 _{+ 3a}2_{b + 3a}2_{c + 3ab}2 _{+ 6abc} + 3ac2 _{+ 1b}3 _{+ 3b}2_{c + 3bc}2 _{+ 1c}3_{, (a +} b + c)4 _{= 1a}4 _{+ 4a}3_{b + 4a}3_{c + 6a}2_b2 ₊ 12a2_{bc + 6a}2_c2 _{+ 4ab}3 _{+ 12ab}2_{c +} 12abc2 _{+ 4ac}3 _{+ 1b}4 _{+ 4b}3_{c + 6b}2_c2 ₊ 4bc3 _{+ 1c}4_.

Dari contoh uraian di atas, terlihat bahwa jumlah suku-suku dari uraian (a + b + c)n _{dimana n = 0, 1, 2, 3, 4,} … berturut-turut adalah 1, 3, 6, 10, 15, … yang merupakan bilangan segitiga.

Ekspansi pertama: (a + b + c)0

mempunyai koefesien tunggal yaitu 1.

Ekspansi kedua: (a + b + c)1

mempunyai koefesien: 1a + 1b + 1c yang diwakili oleh segitiga lapis pertama dengan angka-angka hanya pada titik-titik sudutnya.

1 1 1

Ekspansi ketiga: (a + b + c)2

mempunyai koefesien: 1a2 _{+ 2ab +} 2ac + 1b2 _{+ 2bc + 1c}2 _{yang dapat} disusun dalam segitiga lapis kedua, yaitu

1 2 2 1 2 1

Ekspansi keempat: (a + b + c)3 mempunyai koefesien: 1a3 _{+ 3a}2_{b +} 3a2_{c + 3ab}2 _{+ 6abc + 3ac}2 _{+ 1b}3 ₊ 3b2_{c + 3bc}2 _{+ 1c}3 _{yang dapat disusun} dalam segitiga lapis ketiga, yaitu

1 3 3 3 6 3 1 3 3 1 Ekspansi kelima: (a + b + c)4 mempunyai koefesien: 1a4 _{+ 4a}3_{b +} 4a3_{c + 6a}2_b2 _{+ 12a}2_{bc + 6a}2_c2 _{+ 4ab}3 + 12ab2_{c + 12abc}2 _{+ 4ac}3 _{+ 1b}4 ₊ 4b3_{c + 6b}2_c2 _{+ 4bc}3 _{+ 1c}4 _{yang dapat}

disusun dalam segitiga lapis

keempat, yaitu 1 4 4 6 12 6 4 12 12 4 1 4 6 4 1

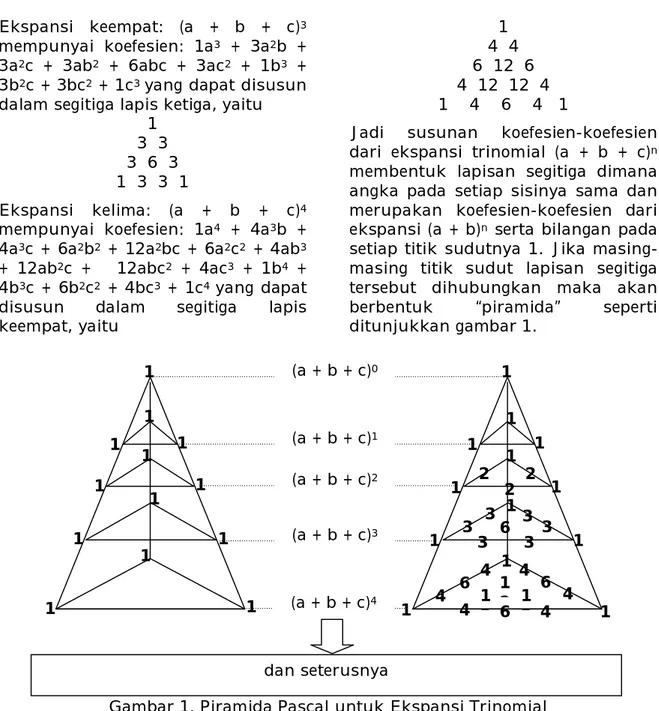
Jadi susunan koefesien-koefesien

dari ekspansi trinomial (a + b + c)n membentuk lapisan segitiga dimana angka pada setiap sisinya sama dan merupakan koefesien-koefesien dari ekspansi (a + b)n _{serta bilangan pada} setiap titik sudutnya 1. Jika masing-masing titik sudut lapisan segitiga tersebut dihubungkan maka akan

berbentuk “piramida” seperti

ditunjukkan gambar 1.

Gambar 1. Piramida Pascal untuk Ekspansi Trinomial

Konstruksi bilangan-bilangan di atas

merupakan pengembangan dari

segitiga pascal, sehingga konstruksi koefesien-koefesien dari uraian (a + b

+ c)n _{tersebut dikenal dengan}

Piramida Pascal (Posamentier, 1990:

432).

1) Hubungan antara Segitiga Pascal dan Piramida Pascal

Di dalam piramida Pascal tampak bahwa bilangan-bilangan pada setiap sisi segitiga merupakan

bilangan-bilangan baris bersesuaian dari

segitiga Pascal. Misalnya bilangan-bilangan pada tiap sisi dari (a + b +

c)3 _{adalah 1 3 3 1 sama dengan} bilangan-bilangan baris ke-5 dalam

segitiga pascal. Hubungan ini

merupakan petunjuk untuk

menentukan metode dalam

menurunkan piramida pascal, yaitu sebagai berikut.

Misalkan bilangan-bilangan pada

setiap sisi dari ekspansi trinomial (a + b + c)n _{diwakili oleh} bilangan-bilangan pada baris yang bersesuaian dari segitiga Pascal. Buatlah segitiga Pascal sampai bilangan baris ke-n+1.

Kemudian kalikanlah

bilangan-bilangan tiap baris dari segitiga

Pascal dengan bilangan-bilangan

dan seterusnya 1 1 1 1 1 1 2 2 2 1 1 1 3 3 1 3 3 3 1 6 3 1 1 2 4 6 6 4 1 2 4 1 4 2 4 6 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (a + b + c)0 (a + b + c)4 (a + b + c)3 (a + b + c)2 (a + b + c)1

pada baris terakhir secara berurutan. Hasil ini menunjukkan koefesien-koefesien dari ekspansi trinomial yang dicari.

Sebagai contoh, menentukan

koefesien dari (a + b + c)4_.

Bilangan-bilangan pada sisi tepi dari (a + b + c)4 _{adalah 1 4 6 4 1. Bilangan} ini merupakan bilangan baris ke-5 dari segitiga Pascal yang merupakan koefesien dari ekspansi (a + b)4_.

Tabel 1. Menentukan koefesien dari (a + b + c)4 bilangan baris ke-5

dari segitiga Pascal

Segitiga Pascal sampai baris ke-5

Koefesien dari ekspansi (a + b + c)4 1 × 4 × 6 × 4 × 1 × 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 4 4 6 12 6 4 12 12 4 1 4 6 4 1

2) Penerapan Piramida Pascal

Untuk Ekspansi Trinomial

( + + )

Langkah-langkah menguraikan (a + b + c)n _{adalah: 1) menentukan susunan}

koefesien-koefesien (segitiga)

menggunakan piramida pascal dan 2) menggunakan koefesien-koefesien itu untuk menentukan ekspansi dari (a + b + c)n _{menurut suku-sukunya,} dengan aturan sebagai berikut.

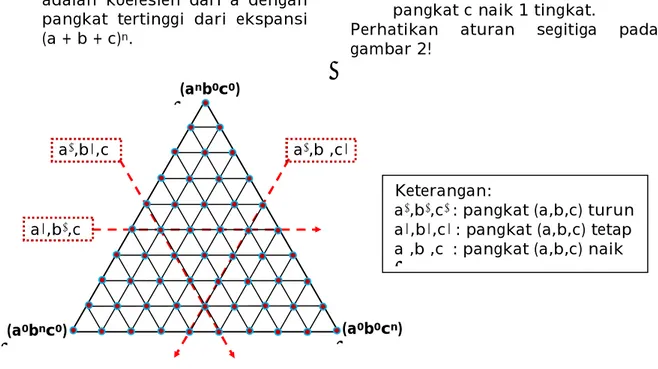
1. Bilangan baris ke-1 dari segitiga adalah koefesien dari a dengan pangkat tertinggi dari ekspansi (a + b + c)n_.

2. Bilangan-bilangan pada setiap

baris merupakan

koefesien-koefesien dari perkalian antara

variabel a dengan pangkat

turun 1 tingkat dari baris sebelumnya dan variabel lain dengan pangkat naik 1 tingkat dari baris sebelumnya sehingga derajat tiap suku sama dengan n.

3. Dalam 1 baris pangkat a tetap sedangkan pangkat b turun 1 tingkat dari kiri ke kanan dan pangkat c naik 1 tingkat.

Perhatikan aturan segitiga pada

gambar 2!

Gambar 2. Ilustrasi Aturan Penggunaan Piramida Pascal

3) Rumus Umum dari Ekspansi Trinomial ( + + )

Sebelum membahas rumus umum untuk ekspansi (a + b + c)n_{, akan} a|_,b↓_,c↑

(an_b0_c0₎

(a0_bn_c0_{) (a}0_b0_cn₎

a↓_,b|_,c↑ _a↓_,b↑_,c|

Keterangan:

a↓_,b↓_,c↓_{: pangkat (a,b,c) turun} a|_,b|_,c|_{: pangkat (a,b,c) tetap} a↑_,b↑_,c↑_{: pangkat (a,b,c) naik}

diuraikan kembali mengenai piramida Pascal yang dikembangkan

dari segitiga Pascal. Dengan

menggunakan notasi kombinasi

maka segitiga Pascal dapat dituliskan sebagai berikut.       0 0       0 1       1 1       0 2       1 2       2 2 ………..       0 r       1 r       2 r … _      j r … _      2 r r       1 r r       r r ……….       0 n _      1 n       2 n … _      r n … _      2 n n       1 n n       n n

Susunan koefesien-koefesien dari

ekspansi trinomial (a + b + c)n _pada

piramida Pascal diperoleh dengan cara sebagai berikut.

      0 n ×       1 n ×       2 n × …       r n × …       n n ×       0 0       0 1       1 1       0 2       1 2       2 2 ………..       0 r       1 r       2 r … _      j r … _      2 r r       1 r r       r r ……….       0 n       1 n       2 n … _      r n … _      2 n n       1 n n       n n

Dengan menggunakan aturan

tersebut, maka formula umum untuk

ekspansi (a + b + c)n _dapat

ditentukan sebagai berikut. (a + b + c)n ₌       0 n [ _      0 0 an_{] +}       1 n [ _      0 1 a n-1_{b +}       1 1 an–1_{c] +}       2 n [ _      0 2 an-2_b2 ₊       1 2 an-2_{bc +}       2 2 an-2_c2_{] + … +}       r n [ _      0 r an-r br ₊       1 r an-r _br-1 _{c +}       2 r an-r _br-2 _c2 _{+ …} + _      j r an-r _br-j _cj _{+ … +}       r r an-r _cr_{] + … +}       1 n n [ _       0 1 n a bn-1 ₊        1 1 n a bn-2_{c +} … + _        2 n 1 n abcn-2 ₊         1 n 1 n acn-1_{] +}       n n [ _      0 n bn ₊       1 n bn-1_{c +}       2 n bn-2_c2 _{+ … +}       1 n n bcn-1 ₊       n n cn_]

Bentuk umum suku-suku dari

ekspansi (a + b + c)n _yang koefesien-koefesiennya baris ke-r+1 adalah:

      r n [ _      0 r an-r _br ₊       1 r an-r _br-1 _{c +}       2 r an-r br-2 _c2 _{+ … +}       j r an-r _br-j _cj _{+ … +}       r r a n-r _cr_{] atau}       r n  _       r 0 j j r an – r _br – j _cj

Dengan demikian ekspansi (a + b + c)n _{dapat ditulis secara singkat} sebagai berikut. (a + b + c)n ₌       0 n [ _      0 0 an_{] +}       1 n  _       1 0 j j 1 an – 1 _b1 – j _cj ₊       2 n  _       2 0 j j 2 an – 2 _b2 – j _cj ₊ … + _      r n  _       r 0 j j r an - r _br - j _cj _{+ … +}       1 n n  _         1 n 0 j j 1 n a bn - j - 1 _cj ₊       n n  _       n 0 j j n bn - j _cj atau (a + b + c)n _{= }        n 0 r r n  _       r 0 j j r an - r _br - j _cj =  _       n 0 r r n an - r _        r 0 j j r br - j _cj

Jadi rumus umum dari ekspansi trinomial (a + b + c) adalah seperti ditunjukkan rumus 2.

.... (2)

b. Piramida Pascal untuk Ekspansi (a + b + c + d)n

Pada pembahasan sebelumnya,

terlihat bahwa segitiga pascal dapat dikembangkan dalam menentukan konfigurasi koefesien-koefesien dari ekspansi (a + b + c)n _{yang dikenal} Piramida Pascal. Selanjutnya, apakah metode tersebut dapat dikembangkan untuk ekspansi polinomial (a + b + c + d)n_{, (a + b + c + d + e)}n _dan seterusnya. Oleh karena itu, akan diselidiki dulu formula dari ekspansi (a + b + c + d)n _{sebagai berikut.}

Pertama, ekspansi (a + b + c + d)0 menghasilkan koefesien tunggal yaitu 1

Kedua, ekspansi (a + b + c + d)1 memiliki koefesien-koefesien : 1a + 1b + 1c + 1d yang diwakili oleh piramida dengan elemen 1 pada tiap titik sudutnya.

Ketiga, ekspansi (a + b + c + d)2 memiliki koefesien-koefesien : 1a2 ₊

2ab + 2ac + 2ad + b2 _{+ 2bc + 2bd + c}2 + 2cd + d2 _{yang diwakili oleh} piramida dengan konfigurasi sebagai berikut.

Terlihat bahwa koefesien-koefesien pada tiap rusuk sama, yaitu 1 2 1 yang merupakan baris ke-3 dari

segitiga pascal dan

koefesien-koefesien pada tiap bidang piramida juga sama:

1 2 2 1 2 1

yang merupakan bilangan segitiga baris ke-3 dari piramida pascal.

Langkah-langkah menentukan

konfigurasi koefesien dari ekspansi (a + b + c + d)n_{, pada dasarnya sama}

dengan langkah-langkah

menentukan konfigurasi koefesien dari ekspansi trinomial.

1

2

2

2

1

1

1

2

2

2

1

1

1

1

(a + b + c)

n

=

 _       n 0 r r n

a

n - r  _       r 0 j j r

b

r - j

c

j

Contoh ekspansi (a + b + c + d)4

1. Koefesien-koefesien tiap rusuk piramida unit untuk ekspansi (a + b + c + d)4 _{adalah 1 4 6 4 1} yang merupakan baris ke-5 dari segitiga pascal.

2. Piramida unit untuk ekspansi (a + b + c + d)4 _{dibentuk dari} piramida pascal untuk ekspansi (a + b + c)n _dengan

koefesien-koefesien pada segitiga alas

adalah koefesien dari ekspansi (a + b + c)4_{, yaitu:}

3. Kalikanlah koefesien-koefesien

pada tiap segitiga unit dari

piramida pascal secara

berturutan dengan: 1 4 6 4 1 sehingga diperoleh piramida unit untuk ekspansi (a + b + c)4_. Hubungan antara segitiga Pascal dan piramida Pascal ditunjukkan oleh gambar 3.

Gambar 3. Menentukan Koefesien dari ekspansi (a + b + c + d)4

Cara I

Cara II

1 4 4 4 6 12 12 12 6 6 4 6 12 4 ₁₂ 6 12 4 24 12 1 12 4 6 6 4 12 1 12 4 4 6 4 1 1 1 1 1 1 1 2 2 2 1 1 1 3 3 1 ₃ 3 3 1 6 3 1 12 4 6 6 4 12 4 12 4 4 6 4 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 ₁ 1 3 1 2 3 1 2 1 1 1 1 3 1 3 1 4 6 4 1 1 1x 1x 4x 6x 4x 1x 3x 1x 3x 1x 2x 1x 1x 1x 1x x1x x4x x6x x4x x1x

1

4 4

6 12 6

4 12 12 4

1 4 6 4 1

1) Aturan Penggunaan Piramida Pascal untuk Ekspansi (a + b + c + d)n _.

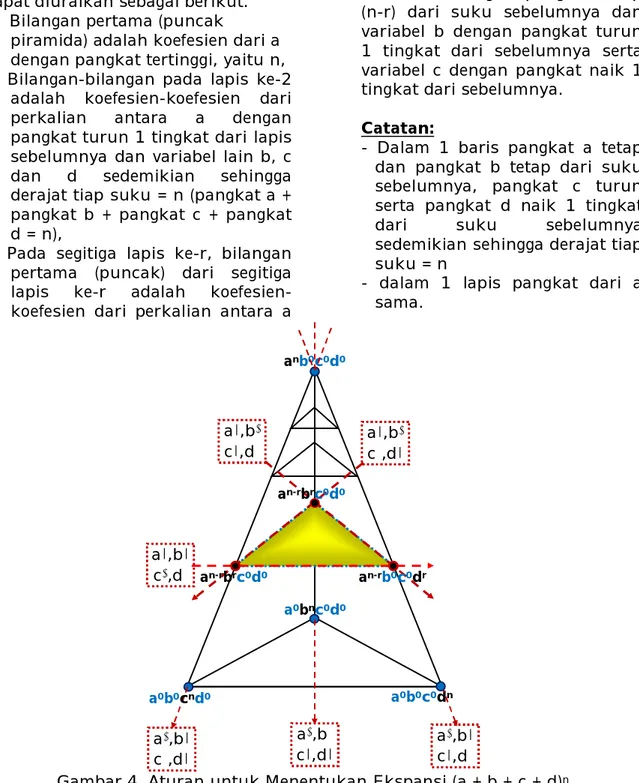
Aturan dari penggunaan piramida pascal untuk ekspansi (a + b + c + d)n dapat diuraikan sebagai berikut. a) Bilangan pertama (puncak

piramida) adalah koefesien dari a dengan pangkat tertinggi, yaitu n, b) Bilangan-bilangan pada lapis ke-2 adalah koefesien-koefesien dari

perkalian antara a dengan

pangkat turun 1 tingkat dari lapis sebelumnya dan variabel lain b, c

dan d sedemikian sehingga

derajat tiap suku = n (pangkat a + pangkat b + pangkat c + pangkat d = n),

c) Pada segitiga lapis ke-r, bilangan pertama (puncak) dari segitiga

lapis ke-r adalah

koefesien-koefesien dari perkalian antara a

dengan pangkat n-r dan variabel b dengan pangkat r, sedangkan koefesien pada baris ke-2 dari

lapis ke-r adalah

koefesien-koefesien dari perkalian antara variabel a dengan pangkat tetap (n-r) dari suku sebelumnya dan variabel b dengan pangkat turun 1 tingkat dari sebelumnya serta variabel c dengan pangkat naik 1 tingkat dari sebelumnya.

Catatan:

- Dalam 1 baris pangkat a tetap dan pangkat b tetap dari suku sebelumnya, pangkat c turun serta pangkat d naik 1 tingkat

dari suku sebelumnya

sedemikian sehingga derajat tiap suku = n

- dalam 1 lapis pangkat dari a sama.

Gambar 4. Aturan untuk Menentukan Ekspansi (a + b + c + d)n

2) Formula Umum dari Ekspansi (a + b + c + d)n_.

Untuk menentukan formula umum dari ekspansi (a + b + c + d)n _akan

ditinjau kembali proses yang

diuraikan sebelumnya, yaitu 1)

menentukan konfigurasi koefesien-koefesiennya dan 2) menggunakan koefesien-koefesien tersebut untuk ekspansi (a + b + c + d)n_{. Dengan}

menggunakan kombinasi maka

konfigurasi koefesien-koefesien dari a|_,b↓ c↑_,d| a|_,b↓ c|_,d↑ a|_,b| c↓_,d↑ _an-r_br_c0_d0 an-r_br_c0_d0 an-r_b0_c0_dr an_b0_c0_d0 a0_b0_c0_dn a0_bn_c0_d0 a0_b0_cn_d0 a↓_,b| c↑_,d| a↓_,b↑ c|_,d| a↓_,b| c|_,d↑

ekspansi (a + b + c + d)n _{dapat ditulis} sebagai berikut.

Dengan menggunakan aturan

tersebut maka formula umum dari ekspansi (a + b + c + d)n _dapat dirumuskan sebagai berikut.

(a + b + c + d)n ₌       0 n [ _      0 0       0 0 an_{] +}       1 n [ _      0 1       0 0 an-1 _{b +}       1 1 ( _      0 1 an–1_{c +}       1 1 an - 1 _{d) +}       2 n [ _      0 2       0 0 an-2_b2 ₊       1 2 ( _      0 1 an-2_{bc +}       1 1 an – 2 _{bd) +}       2 2 ( _      0 2 a n-2_c2 ₊       1 2 an-2_{cd +}       2 2 an-2 _d2_{)] + … +}       r n [ _      0 r       0 0 an-r _br ₊       1 r ( _      0 1 an-r _br-1 _c + _      1 1 an-r _br-1 _{d ) +}       2 r ( _      0 2 an-r _br-2 _c2 + _      1 2 an-r _br-2 _{cd +}       2 2 an-r _br-2 _d2 _{) +} … + _      j r ( _      0 j an-r _br-j _cj ₊       1 j an-r _br-j _cj – 1 _{d +}       2 j an-r _br-j _cj – 2 _d2 _{+ … +}       m j         0 0         2 2         0 2         0 1         0 1         1 2         0 j         1 j         2 j         2 -j j         1 -j j         j j         m j         0 r         1 r         2 r         2 -r r         1 -r r         r r         j r         0 0         0 0         0 1         0 1         0 0         2 2         0 2         0 1         0 1         1 2         0 0         2 2         0 2         0 1         0 1         1 2         0 r         1 r         2 r         2 -r r         1 -r r         r r         j r         0 n         1 n         2 n         2 -n n         1 -n n         n n         r n

×

        0 n         1 n         2 n         r n         n n

×

        0 2         1 2         2 2

×

        0 2         2 2

×

        0 0

×

        0 r         1 r         2 r         j r         r r         n n         0 n

       1 n         2 n         r n

×

an-r _br-j _cj – m _dm _{+ … +}       1 j j an-r _br-j _c dj – 1 ₊       j j an-r _br-j _dj _{) + … +}       r r ( _      0 r an-r _cr ₊       1 r an-r _cr – 1 _{d +}       2 r an-r _cr – 2 d2 _{+ … +}       j r an-r _cr – j _dj _{+ … +}       1 r r an-r _{c d}r – 1 ₊       r r an-r _dr _{)] + … +}       n n [       0 n       0 0 bn ₊       1 n ( _      0 1 bn-1_{c +}       1 1 bn-1_{d )} + _      2 n ( _      0 2 bn-2_c2 ₊       1 2 bn-2_{cd +}       2 2 b n-2_d2 _{) + … +}       r n ( _      0 r bn – r _cr ₊       1 r bn – r cr– 1 _{d +}       2 r bn – r _cr – 2 _d2 _{+ … +}       j r bn – r _cr – j _dj _{+ … +}       r r bn - r _dr _{) +}       n n (       0 n cn ₊       1 n cn – 1 _{d +}       2 n cn – 2 _d2 _{+ …} + _      r n cn – r _dr _{+ … +}       n n dn _)]

Bentuk umum suku-suku dengan

koefesien-koefesien pada segitiga

lapis ke-r dari piramida Pascal dapat ditulis sebagai berikut.

Suku-suku pada segitiga ke-r = _

     r n [       0 r       0 0 an-r _br ₊       1 r ( _      0 1 an-r _br-1 _{c +}       1 1 an-r _br-1 _{d ) +}       2 r ( _      0 2 an-r _br-2 _c2 ₊       1 2 an-r _br-2 _{cd +}       2 2 an-r _br-2 _d2 _{) + …} + _      j r ( _      0 j an-r _br-j _cj ₊       1 j an-r _br-j _cj – 1 _d + _      2 j an-r _br-j _cj – 2 _d2 _{+ … +}       m j an-r _br-j cj – m _dm _{+ … +}       1 j j an-r _br-j _{c d}j – 1 ₊       j j an-r _br-j _dj _{) + … +}       r r ( _      0 r an-r _cr ₊       1 r an-r _cr – 1 _{d +}       2 r an-r _cr – 2 _d2 _{+ …} + _      j r an-r _cr – j _dj _{+ … +}       1 r r an-r _{c d}r – 1 ₊       r r an-r _dr _)] Atau

Suku-suku pada segitiga ke-r = _

     r n  _       r 0 j j r  _       j 0 m m j an – r _br – j _cj – m _dm = _      r n an – r _        r 0 j j r  _       j 0 m m j br – j _cj – m _dm

Karena r bergerak dari 0  n maka rumus umum untuk ekpansi (a + b + c + d)n _{seperti ditunjukkan rumus 3.}

…. (3)

c. Piramida Pascal untuk Ekspansi (a + b + c + d + e)n

Bentuk geometri dari konfigurasi koefesien-koefesien dari ekspansi 5 suku dapat dilihat pada lampiran, yang merupakan pengembangan dari

segitiga pascal juga. Dengan

demikian konfigurasi

koefesien-koefesien dari ekspansi dengan 3

suku, 4 suku, dan 5 suku atau lebih

dapat diwakili oleh

bilangan-bilangan yang membentuk piramida pascal.

Dengan berpedoman pada formula umum dari ekspansi 3 suku, dan 4 suku maka formula/rumus umum dari ekspansi 5 suku dapat ditulis seperti ditunjukkan rumus 4.

(a + b + c + d)n _{= = }        n 0 r r n an – r _        r 0 j j r br – j _        j 0 m m j cj – m _dm

…. (4)

d. Ekspansi Polinomial ( + +

+ ⋯ + )

Dengan mengacu pada metode yang telah diuraikan sebelumnya, maka

rumus umum untuk ekspansi

polynomial dengan k suku yang berbeda dapat ditentukan.

Misalkan suku-suku tersebut: a1, a2, a3, … , ak dengan k bilangan asli, n bilangan cacah, maka rumus umum

dari ekspansi polinomial

ditunjukkan oleh rumus 5. (a1+a2+a3+…+ak)n = ₁n r1 n 0 1 r 1 a r n _   _      2 r 1 r 2 1 r 0 2 r 2 1 a r r _   _       _{r2 r3} 3 2 r 0 3 r 3 2 a r r _   _       …  _           i r 0 1 i r 1 i r i r i 1 i i _a r r …  _            1 k r 0 k r k r k k r 1 k r 1 k k 1 k _{a a} r r …. (5) untuk i = 1, 2, 3, … , k-1, k bilangan asli dan n bilangan cacah

3. Simpulan dan Saran

Berdasarkan uraian pada

pembahasan, maka bentuk umum

dari ekspansi polynomial dapat

disederhanakan sebagai berikut.

Tabel 2. Rangkuman Hasil Pengembangan

Banyak suku

Bentuk ekspansi

Bentuk

Geometris Formula/Rumus umum

2 (a + b)n _{Segitiga Pascal} (lampiran 1)         n 0 k k n an-k _bk 3 (a+b+c)n _Piramida Pascal (lampiran 2)  _       n 0 r r n an – r _        r 0 j j r br – j _cj 4 (a+b+c+d)n _Piramida Pascal 1 derivatif (lampiran 3)  _       n 0 r r n an – r _        r 0 j j r br – j  _       j 0 m m j cj – m _dm 5 (a+b+c+d+e)n _Piramida Pascal 2 derivatif (lampiran 4)  _       n 0 r r n an – r _        r 0 j j r br – j _        j 0 m m j cj – m  _       m 0 s s m dm – s _es … … … … k (a1+a2+a3+…+ ak)n Piramida Pascal (k-3) derivatif 1 r n 1 n 0 1 r 1 a r n _   _      r1 r2 2 1 r 0 2 r 2 1 a r r _   _       3 r 2 r 3 2 r 0 3 r 3 2 a r r _   _       …  _           i r 0 1 i r 1 i r i r i 1 i i _a r r …  _            1 k r 0 k r k r k k r 1 k r 1 k k 1 k _{a a} r r (a + b + c + d + e)n _{= }        n 0 r r n an – r _        r 0 j j r br – j _        j 0 m m j cj – m _        m 0 s s m dm – s _es

DAFTAR PUSTAKA

Naga, Dali S. 1980. Berhitung Sejarah dan Pengembangannya. Jakarta: PT Gramedia.

Posamentier, Alfred S. dan Jay Stepelmen. 1990. Teaching Secondary School

Mathematics Techniques and Enrichment Units Third Edition. Merril

Publishing Company Columbus.

Tentang Penulis:

I Wayan Puja Astawa. Lahir di Selumbung tanggal 16 Januari 1981. Pendidikan yang pernah ditempuh S1 Pendidikan Matematika IKIP Negeri Singaraja dan S2 Pendidikan matematika di Pascasarjana Undiksha Singaraja. Bertugas di SMK Negeri 1 Abang, Karangasem, Bali sejak tahun 2003 sampai sekarang. Aktif sebagai ketua MGMP Matematika Kabupaten Karangasem.

Piramida Pascal untuk Ekspansi (a + b)

n n = 2 1 n = 4 n = 1 n = 0 n = 3 1 1 1 2 1 1 1 3 3 1 1 4 6 4

Piramida Pascal untuk Ekspansi (a + b + c)

n n = 2 1 n = 4 n = 1 n = 0 n = 3 1 1 1 1 1 1 2 2 2 1 1 1 3 3 3 3 6 3 3 4 6 4 1 4 6 12 4 12 12 1 4 6 4 1

Piramida Pascal 1 Derevatif untuk Ekspansi (a + b + c + d)

n n = 2 1 n = 4 n = 1 n = 0 n = 3 1 1 1 1 1 2 2 2 1 1 1 2 2 2 1 3 3 3 1 1 1 3 3 3 3 6 3 3 4 6 4 1 4 6 12 4 12 12 1 4 6 4 1 4 4 4 6 6 6 12 12 12 4 4 4 12 12 12 12 24 12 12 3 3 3 6 6 6 1

Piramida Pascal 2 Derevatif untuk Ekspansi (a + b + c + d + e)

n n = 1 n = 0 n = 2 n = 3 1 1 1 1 1 1 1 2 2 2 2 1 2 2 2 1 1 1 2 2 2 1 3 3 3 3 3 6 6 6 3 3 3 6 6 6 1 1 1 3 3 3 3 6 3 3 1 3 3 3 3 3 3 6 6 6 4 4 4 12 12 24 12 12 12 12 4 4 4 6 6 6 12 12 12 1 4 6 4 1 4 6 12 4 12 12 1 4 6 4 1 4 4 4 4 6 12 12 12 6 6 6 12 12 12 1 1 4 12 12 12 12 24 12 12 4 12 12 12 12 12 12 24 24 24 1 n = 4