Statistika -Ukuran Penyebaran data : Penjelasan Rumus dan Contoh Soal Jangkauan, Simpangan, Ragam Terlengkap Ukuran penyebaran data

Statistika -Ukuran Penyebaran data : Penjelasan Rumus

dan Contoh Soal Jangkauan, Simpangan, Ragam

Terlengkap

Ukuran penyebaran data

Dalam pengukuran statistika terdpat pula Ukuran Penyebaran data. Ukuran penyebaran data

merupakan ukuran yang menunjukkan seberapa jauh data menyebar dari rata-rata. Terdapat

ukuran penyebaran data yang akan kita pelajari pada artikel ini, yaitu Jangkauan (range),

Simpangan rata-rata, Ragam (variasi), dan Simpangan Baku. namun, sebelum anda

mempelajari postingan ini, sebaiknya anda baca dulu materi sebelumnya tentang

pengertian

Statistika

,

Ukuran Pemusatan data

Dan

Ukuran Letak Data

.

Penjelasan dan uraian lengkapnya akan dijelaskan pada penjelasan di bawah ini.

Jangkauan (Range)

Jangkauan merupakan selisih data terbesar dan data terkecil. Jangkauan sering dilambangkan

dengan R.

1. Jangkauan Data

R = x

maks

– x

min

Keterangan:

R = jangkauan

X

maks

= data terbesar

X

min

= data terkecil

Contoh Soal Jangkauan Data

Tentukan jangkauan dari data : 3,6,10,5,8,9,6,4,7,5,6,9,5,2,4,7,8.

Jawab :

R = x

maks

– x

min

= 10-2 = 8

Jadi, jangkaun data tersebut adalah 8.

2. Jangkauan interkuartil

Jangkauan interkuartil adalah selisih antara kuartil ketiga dan kuartil pertama.

H = Q

3

– Q

1

Keterangan :

H = jangkauan interkuartil

Q

3

= kuartil ketiga

Q

1

= kuartil pertama

3. Simpangan kuartil ( jangkauan semi interkuartil)

Singan kuartil adalah setengah dari selisih kuartil ketiga dan kuartil pertama.

Sk = ½ Q

3

– Q

1

Keterangan :

Sk = simpangan kuartil

Q

3

= kuartil ketiga

Q

1

= kuartil pertama

Simpangan Rata- Rata

Simpangan rata-rata merupakan nilai rata-rata dari selisih setiap data dengan nilai mean atau

rataan hitungnya. Simpangan rata-rata sering dilambangkan dengan SR.

1. Data Tunggal

Keterangan :

SR = simpangan rata-rata

Xi = data ke-i

X = rataan hitung

n = banyak data

Contoh Soal Simpangan Rata rata Data tunggal

Tentukan simpangan rata-rata dari data 4,6,8,5,4,9,5,7.

Jawab :

Jadi, simpangan rata-ratanya adalah 1,5

2. Data Bergolong (Berkelompok)

Keterangan :

SR = simpangan rata-rata

Xi = data ke-i

X = rataan hitung

fi = frekuensi data ke-i

Contoh Soal Simpangan Rata rata Data Berkelompok

Tentukan simpangan rata-rata dari data berikut:

Data

f

41-45

6

46-50

3

51-55

5

56-60

8

61-65

8

Jawab:

Data

f

x

i

f

i

x

i

|x

i

-x|

Fi|x

i

-x|

41-45

6

43

258 11,5

69

46-50

3

48

114 6,5

19,5

51-55

5

53

265 1,5

7,5

56-60

8

58

464 3,5

28

61-65

8

63

504 8,5

68

Jumlah 30

1.635

165

Jadi, simpangan rata-ratanya adalah 5,5.

Ragam

Ragam atau variasi adlah nilai yang menunjukkan besarnya penyebaran data pada kelompok

data. Ragam atau variasi dilambangkan dengan s

2

_.

1. Variasi untuk data tunggal

Keterangan :

s

2

_{= variasi}

x

i

= data ke –i

x = rataan hitung

n = banyak data

2. Variasi untuk data bergolong (berkelompok)

Keterangan :

s

2

_{= variasi}

x

i

= data ke –i

x = rataan hitung

fi = frekuensi data ke-i

Simpangan baku

Simpangan baku atau disebut juga deviasi standar merupakan akar dari jumlah kuadrat diviasi

dibagi banyaknya data. Simpangan baku sering dilambangkan dengan s.

Keterangan :

S = simpangan baku

x

i

= data ke –i

x = rataan hitung

n = banyak data

2. Simpangan baku untuk data bergolong (berkelompok)

Keterangan :

s = simpangan baku

x

i

= data ke –i

x = rataan hitung

fi = frekuensi data ke-i

Contoh Soal Simpangan Baku

Tentukan variari dan simpangan baku dari data : 4,6,8,7,9,8.

Data f

41-45 6

46-50 3

51-50 5

56-60 8

61-65 8

Jawab :

Data

f

x

i

f

i

x

i

(x

i

-x)

2

f

i

(x

i

-x)

2

41-45

6

43

258

132.25

93.5

46-50

3

48

144

42.25

126.75

51-50

5

53

265

2.25

11.25

56-60

8

58

464

12.25

98

61-65

8

63

504

72.25

578

Jumlah 30

1.635

676

Jadi, variasinya = 22,53 dan simpangan bakunya = 4,75.

Statistika : Ukuran Penyebaran Data

Blog Koma

- Dengan menentukan pemusatan data dan ukuran letak data ternyata

belum cukup untuk memberikan gambaran yang jelas dari suatu data. Pada pengukuran

statistika, selain ukuran pemusatan dan ukuran letak, juga ada

Ukuran Penyebaran Data

.

Ukuran penyebaran data adalah ukuran yang menunjukkan seberapa jauh data suatu

menyebar dari rata-ratanya. Pada

ukuran penyebaran data

, kita akan mempelajari materi

Jangkauan (Range), Simpangan, Ragam (Variansi), ukuran penyebaran pada nilai

kuartil,

dan

Pencilan (Outlier)

. Sebelum membaca tentang ukuran penyebaran data,

sebaiknya kita baca dulu materi "Statistika Secara Umum" dan "Statistika : Penyajian Data".

Jangkauan (Range)

Jangkauan sering disebut range atau rentang. Jangkauan dari suatu data didefinisikan

sebagai selisih antara data terbesar dengan data terkecil. Disini kita simbolkan jangkauan

dengan huruf R.

Rumus umum jangkauan (range) :

Keterangan :

X

min

=

nilai atau data terkecil

X

maks

=

nilai atau data terbesar

♣

Jangkauan data tunggal

Untuk jangkauan data tunggal, langsung tentukan nilai terbesar dan terkecilnya, lalu

dikurangkan.

Contoh

Tentukan jangkauan(range) dari data-data di bawah ini.

6, 7, 3, 4, 8, 3, 7, 6, 10, 15, 20

Penyelesaian :

Dari data di atas diperoleh

x

maks

=20

dan

x

min

=3

*). Menentukan jangkauannya :

R

=

x

maks

−

x

min

=20−3=17

Jadi, jangkauan data tersebut adalah 17.

♣

Jangkauan data Berkelompok

Untuk data bergolong, nilai tertinggi diambil dari nilai tengah kelas tertinggi dan nilai

terendah diambil dari nilai kelas yang terendah.

Contoh

Tentukan range dari tabel berikut ini.

Penyelesaian :

*). Nilai tengah kelas terendah :

x

min

=

3+52

=4

*). Nilai tengah kelas tertinggi :

x

maks

=

18+202

=19

*). Menentukan jangkauannya :

R

=

x

maks

−

x

min

=19−4=15

Jadi, jangkauan data tersebut adalah 15.

Simpangan Rata-rata

Simpangan rata-rata atau deviasi rata-rata adalah ukuran yang menyatakan seberapa

besar penyebaran tiap nilai data terhadap nilai meannya (rata-ratanya).

♠

Simpangan rata-rata data tunggal

Rumus menghitung simpangan rata-rata data tunggal :

Keterangan :

SR

=

Simpangan rata-rata

n

=

ukuran data (total frekuensi)

x

i

=

data ke-

i

dari data

x

1

,

x

2

,

x

3

,...,

x

n

x

¯¯¯

=

rataan hitung.

∑

=

notasi sigma yang artinya jumlahan.

|

x

i

−

x

¯¯¯

|=

harga mutlak dari

x

i

−

x

¯¯¯

yang hasilnya selalu positif.

contoh :

|3|=3

dan

|−3|=3

Contoh :

Diketahui data: 7, 6, 8, 7, 6, 10, 5. Tentukan simpangan rata-ratanya.

Penyelesaian :

*). Menentukan rata-ratanya,

x

¯¯¯

=7+6+8+7+6+10+57=497=7

*). Menentukan simpangan rata-ratanya :

SR

=1

n

∑

i=1n

|

x

i

−

x

¯¯¯

|=17

∑

i=17

|

x

i

−7|=17(|7−7|+|6−7|+|8−7|+|

7−7|+|6−7|+|10−7|+|5−7|)=17(|0|+|−1|+|1|+|0|+|−1|+|3|+|

−2|)=17(0+1+1+0+1+3+2)=17(8)=87

Jadi, simpangan rata-ratanya adalah

87

♠

Simpangan rata-rata data berkelompok

Keterangan :

SR

=

Simpangan rata-rata

n

=

banyak kelas

x

i

=

nilai tengah kelas ke-

i

x

¯¯¯

=

rataan hitung.

f

i

=

frekuensi kelas ke-

i

∑

i=1n

f

i

=

total frekuensi

Contoh :

Tentukan simpangan rata-rata pada tabel berikut ini.

Penyelesaian :

*). Menentukan rata-rata :

x

¯¯¯

=

∑

i=1n

f

i

.

x

i

∑

i=1n

f

i

=630040=157,5

*). Menentukan simpangan rata-ratanya :

SR

=

∑

i=1n

f

i

.|

x

i

−

x

¯¯¯

|

∑

i=1n

f

i

=26040=5,15.

Jadi, simpangan rata-ratanya adalah 5,15.

Simpangan Baku (Standar Deviasi) Data tunggal

Diketahui sekumpulan data kuantitatif yang tidak dikelompokkan dan dinyatakan oleh

x

1

,

x

2

,...,

x

n

. Dari data tersebut, dapat diperoleh nilai simpangan baku (

S

) yang ditentukan

oleh rumus berikut.

Data sampel berlaku untuk

n

<30

dan data populasi untuk

n

≥30

Contoh:

Dari 40 siswa kelas XI IPA diperoleh nilai yang mewakili adalah 7, 9, 6, 3, dan 5. Tentukan

simpangan baku dari data tersebut.

Penyelesaian :

*). Menentukan rata-rata :

x

¯¯¯

=

7+9+6+3+55

=

305

=6

*). Melengkapkan tabel

*). Menentukan simpangan baku

−−−

√

=5√=2,24

Jadi, simpangan bakunya adalah 2,24.

Simpangan Baku (Standar Deviasi) Data Berkelompok

Sekumpulan data kuantitatif yang dikelompokkan, dapat dinyatakan oleh

x

1

,

x

2

,...,

x

n

dan masing-masing data mempunyai frekuensi

f

1

,

f

2

,...,

f

n

. Simpangan baku (

S

) dari data

tersebut diperoleh dengan menggunakan rumus

Data sampel berlaku untuk

n

<30

dan data populasi untuk

n

≥30

Contoh :

Hasil tes Matematika 30 siswa kelas XI IPA seperti ditunjukkan pada tabel di bawah.

Berdasarkan data tersebut, tentukan simpangan bakunya.

Penyelesaian :

*). Menentukan rata-ratanya :

x

¯¯¯

=

∑

i=1n

f

i

.

x

i

∑

i=1n

f

i

=49030=16,33

*). Menentukan simpangan bakunya

s

=

∑

i=15

f

i

.(

x

i

−

x

¯¯¯

)

2

n

−−−−−−−−−−−−

−



⎷



=836,730−−−−−

√

=27,89−−−−−

√

=5,28

Jadi, simpangan bakunya adalah 5,28.

Ragam (Variansi)

Variansi (ragam) adalah rata-rata dari jumlah kuadrat simpangan tiap data. Ragam bisa

dirumuskan sebagai :

Ragam

=

S

2

Artinya ragam diperoleh dari nilai simpangan baku dikuadratkan.

Contoh :

Dari contoh soal yang berkaitan dengan simpangan baku data berkelompok di atas, diperoleh

simpangan bakunya adalah 5,28. Sehingga nilai ragamanya (variansi) adalah :

Ragam

=

S

2

=(5,28)

2

=27,89

Koefisien Keragaman (KK)

Rumus koefisien keragaman (KK) dari sekumpulan data

x

1

,

x

2

,

x

3

,...,

x

n

adalah

KK

=

Sx

¯¯¯

Keterangan :

KK

=

Koefisien Keragaman

S

=

simpangan baku

x

¯¯¯

=

nilai rata-rata data.

Contoh :

Pak Murtono seorang pengusaha. Bidang usaha yang ia jalani adalah penerbitan, tekstil, dan

angkutan. Dalam 5 bulan terakhir, ia mencatat keuntungan bersih ketiga bidang usahanya.

Hasilnya tampak pada Tabel berikut

Jika Pak Murtono berpendapat bahwa bidang usaha yang akan dipertahankan hanya dua

bidang usaha dengan kriteria bidang usaha dengan keuntungan bersih yang stabil, tentukanlah

bidang usaha yang sebaiknya tidak dilanjutkan.

Penyelesaian :

*). Menghitung rataan, simpangan baku, dan koefisien keragaman dari setiap bidang usaha.

i). Bidang usaha penerbitan

x

¯¯¯

SKK

=60+116+100+132+725=96=

∑

i=15

(

x

i

−

x

¯¯¯

)

2

n

−1−−−−

−−−−−−

−



⎷



=(60−96)

2

+(116−96)

2

+(100−96)

2

+(132−96)

2

+(72−

96)

2

5−1−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

−−−−−−−−−−−−−−−−−−

√

=35844−−−−

−

√

=29,93=

Sx

¯¯¯

=29,9396=0,31

ii). Bidang usaha tekstil

x

¯¯¯

SKK

=156=40,69=

Sx

¯¯¯

=40,69156=0,26

ii). Bidang usaha angkutan

x

¯¯¯

SKK

=161,6=100,58=

Sx

¯¯¯

=100,58161,6=0,62

Jadi, sebaiknya Pak Murtono tidak melanjutkan usaha angkutan karena keuntungannya tidak

stabil (nilai KK paling besar).

Ukuran Penyebaran Data pada Nilai Kuartil

Dari data kita bisa menentukan nilai kuartilnya baik kuartil kesatu (

Q

1

), kuartil kedua

(

Q

2

), dan kuatil ketiga (

Q

3

). Untuk cara menentukan nilai kuartil, silahkan baca materi

"Statistika : Ukuran Letak Data". Dari nilai-nilai kuartil tersebut juga berlaku ukuran

penyebaran yaitu Jangkauan antarkuartil (Hamparan) yang kita simbolkan dengan JK dan

Jangkauan semi antarkuartil (Simpangan Kuartil) yang kita simbolkan dengan SK.

Rumus masing-masing :

JK

=

Q

3

−

Q

1

dan

SK

=12(

JK

)=12(

Q

3

−

Q

1

)

Dari nilai penyebaran pada kuartil dikenal juga istilah Langkah (L), yang dirumuskan :

L

=32(

JK

)=32(

Q

3

−

Q

1

)

Catatan :

Buku lain juga menyebutkan istilah Jangkauan antarkuartil = Jangkauan interkuartil dan

Jangkauan semi antarkuartil = Jangkauan semi interkuartil .

Pencilan (Outlier)

Istilah Pagar dalam dan pagar luar :

*). Pagar dalam (PD) adalah nilai data yang berada satu langkah di bawah kuartil pertama.

Rumusnya :

PD

=

Q

1

−

L

*). Pagar luar (PL) adalah nilai data yang berada satu langkah di atas kuartil ketiga..

Rumusnya :

PL

=

Q

3

+

L

Pengertian Pencilan :

Semua data yang nilainya kurang dari pagar dalam atau lebih dari pagar luar disebut

pencilan. Pencilan adalah datum yang memiliki karakteristik berbeda dari datum lainnya.

Dapat dikatakan bahwa pencilan merupakan datum yang tidak konsisten (tidak normal)

dalam kumpulan data.

Contoh :

Hasil tes matematika dari 20 siswa tercatat sebagai berikut.

70, 68, 71, 68, 66, 73, 65, 74, 65, 64, 78, 79, 61, 81, 60, 97, 44, 64, 83, 56.

Jika ada data pencilan, tentukan datum tersebut.

Penyelesaian :

*). Data setelah diurutkan menjadi :

44, 56, 60, 61, 64, 64, 65, 65, 66, 68, 68, 70, 71, 73, 74, 78, 79, 81, 83, 97

ada 20 datum (

n

=20

) .

*). Menentukan nilai kuartil data, jangkauan antarkuartil, langkah, pagar dalam(PD) dan

pagar luar(PL).

Q

1

Q

1

Q

2

Q

2

Q

3

Q

3

JKLPDPL

=

X

14(n+1)

=

X

14(20+1)

=

X

5,25

=

x

5

+0,25(

x

6

−

x

5

)=64+0,25(64−64)=64+0=64=

X

24(n+1)

=

X

24(20+1)

=

X

10,5

=

x

10

+0,5(

x

11

−

x

10

)=68+0,5(68−68)=68+0=68=

X

34(n+1)

=

X

34(20+1)

=

X

15,75

=

x

15

+0,

75(

x

16

−

x

15

)=74+0,75(78−74)=74+3=77=

Q

3

−

Q

1

=77−64=13=32(

J

K

)=32.(13)=19,5=

Q

1

−

L

=64−19,5=44,5=

Q

3

+

L

=77+19,5=96,5

Jadi, ada dua pencilan dalam data ini, yaitu 44 dan 97 karena datum 44 nilainya kurang dari

PD dan datum 97 nilainya lebih besar dari PL.

4. Ukuran Penyebaran Data

Ukuran Penyebaran Data adalah ukuran yang digunakan untuk menyatakan sebaran atau

variasi dari suatu kelompok data. Berikut ini beberapa ukuran yang biasa digunakan :

A. Range/ Jangkauan

Range/Jangkauan adalah perbedaan antara nilai terbesar dan nilai terkecil pada sekelompok

data.

Sifat – sifat :

 Hanya dua nilai yang digunakan

 Dipengaruhi oleh Nilai yang ekstrem

 Mudah dihitung dan dan dipahami

B. Deviasi Absolut Rata-rata

Deviasi Absolut Rata-rata adalah jumlah nilai absolut setiap deviasi dari rata-rata dibagi

banyaknya pengamatan.

Sifat – sifat :

 Tidak terlalu dipengaruhi oleh nilai besar atau kecil

 Seluruh pengamatan digunakan dalam perhitungan

C. Variansi

Variansi adalah rata-rata deviasi kuadrat dari rata-rata hitung.

Rumus Variansi Populasi :

Rumus Variansi Sampel :

Sifat – sifat :

 Seluruh pengamatan digunakan dalam perhitungan

 Tidak terlalu dipengaruhi oleh pengamatan yang ekstrem

 Unitnya agak sulit digunakan, biasanya adalah unit kuadrat awal

D. Standar Deviasi

Standar Deviasi adalah akar kuadrat dari Variansi.

Rumus Standar Deviasi Populasi :

Rumus Standar Deviasi Sampel :

Sifat -sifat :

 Mempunyai satuan yang sama dengan data aslinya

 Merupakan akar kuadrat dari jarak kuadrat rata terhadap nilai rata-rata

 Nilainya pasti positif

 Merupakan ukuran penyebaran data yang paling sering dilaporkan



Home



Matematika SD



Matematika SMP



Matematika SMA



Matematika Dasar



Matematika Umum



Contoh Soal

Home » RUMUS MATEMATIKA SMP » SMP » Ukuran Penyebaran Data Statistika

Ukuran Penyebaran Data Statistika

Ukuran Penyebaran Data Statistika - Di dalam artikel sebelumnya kita

telah bersama-sama mempelajari materi pelajaran matematika

mengenai Ukuran Pemusatan Data yang di dalamnya meliputi Mean,

Median, dan Modus. Pada kesempatan kali ini kita akan belajar mengenai

ukuran penyebaran data. Untuk mengetahui lebih jelas mengenai apa

yang dimaksud dengan ukuran penyebaran data maka sebaiknya kalian

menyimak dengan baik penjelasan yang akan diberikan oleh Rumus

Matematika Dasar berikut ini:

Ukuran penyebaran data adalah nilai ukuran yang memberikan gambaran

mengenai seberapa besar suatu data menyebar dari titik-titik

pemusatannya. Ukuran penyebaran data meliputi jangkauan, kuartil,

jangkauan interkuartil, serta jangkauan semiinterkuartil atau biasa disebut

juga sebagai simpangan kuartil.

Pengertian Jangkauan, Kuartil, Jangkauan Interkuartil, dan

Jangkauan Semiinterkuartil

Jangkauan

Yang dimaksud dengan jangkauan dari suatu data adalah selisih antara

nilai terbesar dan nilai terkecil yang ada di dalam data tersebut.

Jangkauan dapat dirumuskan sebagai berikut:

Jangkauan = data terbesar – data terkecil.

Mari kita simak contoh soal mengenai jangkauan di bawah ini:

Contoh Soal:

Berikut adalah nilai rapor Putri selama 1 semester terakhir:

78 80 85 90 75

94 92 88 89 95

84 85 92 96 87

Tentukanlah jangkauan dari data tersebut!

Penyelesaian:

Data terbesar = 96

Data terkecil = 75

Jangkauan = data terbesar – data terkecil

Jangkauan = 96 – 75

Jangkauan = 21

Kuartil

Kuartil adalah ukuran yang membagi data yang sudah diurutkan menjadi

empat bagian yang sama. Contohnya adalah sebagai berikut:

Data yang berada di batas pengelompokan pertama disebut sebagai

Kuartil Bawah (Q1)

, data yang berada pada batas pengelompokan yang

kedua disebut sebagai

Kuartil Tengah (Q2)

, sedangkan data yang ada

pada batas pengelompokan ketiga disebut dengan

Kuartil Atas (Q3).

Untuk menentukan nilai-nilai kuartil kita harus mengurutkannya lalu

kemudian menentukan kuartil tengahnya terlebih dahulu (Q

2

) yang

merupakan median dari data tersebut. Setelah itu, seluruh data yang ada

di sebelah kiri digunakan untuk mencari kuartil bawah (Q

1

). Nilai Q

1

adalah median dari data yang ada di sebelah kiri Q

2

sedangkan Q

3

adalah

median dari seluruh data yang ada di sebelah kanan Q

2

.

Pada suatu data yang memiliki ukuran yang cukup besar, nilai-nilai kuartil

dapat ditentukan dengan menggunakan rumus berikut ini:

Letak

Qi

= data ke-

i

/4 (

n

+ 1)

i

= 1, 2, dan 3

Rumus tersebut dapat digunakan setelah data diurutkan naik.

Contoh Soal:

Tentukan nilai kuartil dari data berikut:

3 7 7 7 8 8 9 10 11 11 11

Penyelesaian:

Kareana datanya sudah terurut naik, maka kita bisa menentukan nilai Q

1

,

Q2, dan Q

3

sebagai berikut (

n

= 11).

Letak Q

1

= data ke-1/4 (11 + 1) = data ke-3

Karena data ke-3 = 7 maka Q

1

= 7

Letak Q

2

= data ke-2/4 (11 + 1) = data ke-6

Karena data ke-6 = 8 maka Q

2

= 8

Letak Q

3

= data ke-3/4 (11 + 1) = data ke-9

Karena data ke-9 = 11 maka Q

3

= 11

Jangkauan Kuartil dan Jangkauan Semiinterkuartil

Jangkauan interkuartil merupakan selisih antara kuartil atas dan kuartil

bawah. Sehingga dapat dirumuskan menjadi:

Q

R

= Q

3

- Q

1

Sedangkan jangkauan semiinterkuartil merupakan setengah dari

jangkauan interkuartil. Sehingga dapat dirumuskan menjadi:

Q

d

= 1/2 Q

R

atau Q

d

= 1/2(Q

3

- Q

1

)

Contoh Soal:

Tentukan jangkauan, jangkauan interkuartil, dan jangkauan

semiinterkuartil dari data berikut:

3, 5, 1, 4, 2, 7, 9, 6, 6, 8, 7.

Penyelesaian:

Data diurutkan menjadi :

Diketahui:

data terbesar = 9

data terkecil = 1

Q

1

= 3

Q

2

= 6

Q

3

= 7

Jangkauan = data terbesar – data terkecil = 9 – 1 = 8

Jangkauan interkuartil = Q

R

= Q

3

- Q

1

= 7 – 3 = 4

Jangkauan semiinterkuartil = 1/2(Q

3

- Q

1

) = 1/2 x 4 = 2

Demikianlah ulasan lengkap seputar

Ukuran Penyebaran Data

semoga

apa yang telah disampaikan di atas dapat kalian pahami dengan baik.

Sampai bertemu kembali pada pembahasan materi pelajaran matematika

selanjutnya. Selamat belajar!!!

TUGAS MAKALAH

STATISTIKA DESKRIPTIF

“UKURAN PENYEBARAN DATA (SIMPANGAN RATA – RATA , STANDAR

DEVIASI , JANGKAUAN KUARTIL , JANGKAUAN PERSENTIL”

Kelompok 8



Farid Naufal Bayu Agung

11113401



Mariah Ulfah Apriani

11113454



Doni Supriadi

11113473



Cista Daniarti

11113480



Fadhilla Hianing Alsfia

11113489



Ratu Halimatussa’adiyah

11113552



Al Fattah Nur Halim Suhandi

11113622

Dosen : Morinof Hendra

Jakarta

2012

KATA PENGANTAR

Puji syukur kehadirat Tuhan Yang Maha Kuasa atas segala limpahan Rahmat, Inayah,

Taufik dan Hidayah-Nya sehingga kami dapat menyelesaikan penyusunan makalah ini dalam

bentuk maupun isinya yang sangat sederhana.

Penulisan makalah ini digunakan untuk memenuhi salah satu tugas mata pelajaran

Statistika Deskriptif. Oleh karena itu, kami mengucapkan rasa terima kasih kepada :

1. Bapak Morinof Hendra selaku dosen pengajar mata kuliah Statistika Deskriptif

2. Teman-temanku semua yang telah mendukung dan memberi semangat kepada

penulis

Harapan kami semoga makalah ini membantu menambah pengetahuan dan

pengalaman bagi para pembaca, sehingga kami dapat memperbaiki bentuk maupun isi

makalah ini sehingga kedepannya dapat lebih baik.

Makalah ini kami akui masih banyak kekurangan karena pengalaman yang kami

miliki sangat kurang. Oleh kerena itu kami harapkan kepada para pembaca untuk

memberikan masukan-masukan yang bersifat membangun untuk kesempurnaan makalah ini.

Jakarta,26 Mei 2012

Tim penyusun

i

DAFTAR ISI

KATA PENGANTAR...i

DAFTAR ISI...ii

BAB I PENDAHULUAN

1.1 Latar Belakang...1

1.2 Rumusan Masalah...1

1.3 Tujuan...1

BAB II LANDASAN TEORI

2.1 Pengertian Ukuran Penyebaran Data...2

BAB III PEMBAHASAN

3.1 Simpangan Rata - Rata ……….………...3

3.2 Standar Deviasi ...4

3.3 Jangkauan Kuartil...6

3.4 Jangkauan Persentil …. ………...9

BAB IV PENUTUP

4.1 Kesimpulan...10

4.2 Saran...10

DAFTAR PUSTAKA

ii

BAB I

PENDAHULUAN

1.1

Latar Belakang

Pengetahuan kita tentang berbagai macam ukuran sangat diperlukan agar

kita dapat memperoleh gambaran lebih lengkap dalam memahami tentang data

– data yang telah terkumpul . Kita telah memahami dua macam ukuran , yaitu :

1.

Ukuran gejala meliputi rata – rata hitung , rata – rata ukur , rata – rata

harmonic , dan modus .

2.

Ukuran letak meliputi median , kuartil , desil , dan persentil .

Di samping kedua ukuran yang telah kita pahami tersebut kita masih akan

membahas ukuran lain , yaitu simpangan atau ukuran penyebaran . Ukuran

terakhir ini menggambarkan bagaimana terpencarnya sekumpulan data

kuantitatif atau bilangan – bilangan . beberapa ukuran yang akan kami bahas di

dalam makalah ini adalah simpangan rata – rata , standar deviasi , jangkauan

kuartil , dan jangkauan persentil .

1.2

Rumusan Masalah

Pada makalah ini kami merumuskan beberapa hal :

1.

Pengertian ukuran penyebaran data

3.

Standar deviasi

4.

Jangkauan kuartil

5.

Jangkauan persentil

1.3

Tujuan

1.

Untuk memenuhi tugas dari dosen pada mata kuliah Statistika Deskriptif.

2.

Agar pembaca mengerti apa maksud dari ukuran penyebaran data.

1

BAB II

LANDASAN TEORI

2.1

Pengertian Ukuran Penyebaran Data

Setelah mengetahui tentang distribusi frekuensi nilai rata – rata dari data

yang sdang kita teliti , kita juga perlu mengetahui tentang ukuran yang dapat

digunakan untuk mengetahui variabilitas atau penyebaran datanya . Ukuran

yang dimaksud dalam dunia statistik dikenal denga nama variabilitas data atau

ukuran penyebaran data .

Ukuran penyebaran data itu yakni , berbagai macam ukuran statistik yang

dapat digunakan untuk mengetahui luas penyebaran data atau variasi data atau

homogenitas data atau stabilitas data .

2

BAB III

3.1SIMPANGAN RATA-RATA (Mean Deviation)

Simpangan rata-rata (SR) : yang di maksud dengan simpangan (deviation)

adalah selisih antara nilai pengamatan ke I dengan nilai rata-rata atau antara xi

dengan X (X rata-rata) penjumlahan daripada simpangan-simpangan dalam

pengamatan kemudian di bagi dengan jumlah pengamatan , N , di sebut dengan

simpangan rata-rata

Dalam setiap nilai Xi akan mempunyai simpangan sebesar xi-X . karena

nilai xi berfariasai di atas dan dibawah nilai rata-ratanya maka jika nilai

simpangan tersebut di jumblahkan akan sama dengan “nol”.untuk dapat

mengitung rata-rata dari simpangan tersebut maka nilai yang di ambil adalah

nilai “absolute” dari simpangan itu sendiri,artinya tidak menghiraukan apakah

nilai simpangan tersebut positif (+) atau negative (-) rata-rata.



Data tidak bekelompok

SR = 1 ∑|X - X|

n



Data dikelompokan

SR = 1/n ∑f | X - X|

Ketarangan :

SR = Simpangan Rata-rata

X = Nilai data

= NILAI Rata-rata hitung

f = Frekuensi kelas ( data berkelompok )

N = Banyaknya data

3

Contoh soal

Diketahui suatu deretan bilangan 4 ,6 ,9, 5 hitunglah

- simapangan Rata –rata

Jawab :

SR = 1/n ∑ |X-

|

= µ = 1/n

= ¼ (4+6+9+5) = 1/4 . 24 = 6

SR = ¼(|4-6| + |6-6| + |9-6| + |5-6|)

= ¼(2+0+3+1)

=6/4 = 1.5

3.2STANDAR DEVIASI

Dalam kamus bahasa Indonesia istilah deviasi diartikansebagai

penyimpangan. Dalam dunia statistik istilah deviasi adalah simpangan atau

selisih dari masing-masing skor atau interval dari nilai rata-rata hitung

(deviation from the mean). Sedangkan deviasi standar atau standart deviation

adalah pengembangan dari deviasi rata-rata.

Karl Person

memberikan jalan

keluar dari deviasi rata-rata yang kurang dipertanggung jawabkan dengan tidak

membedakan deviasi “Plus” dan deviasi “Minus”. Jalan keluarnya sebagai

berikut:

1.

Mengkuadratkan semua deviasi yang ada baik yang deviasi yang bertanda

“Plus” atau deviasi yang bertanda “Minus”. Dengan demikian baik yang

bertanda “Plus” akan tetap “Plus”, sedangkan yang bertanda “Minus” akan

menjadi “Plus”.

4

2.

Kemudian dari hasil kuadrat dijumlahkan dan dicara rata-ratanya.

3.

Kemudian diakarkan dari rata-rata tersebut

Deviasi standar atau Standart Deviation dilambangkan dengan

SD

atau δ.

Disebut standar deviasi karena merupakan pengembangan dari deviasi rata-rata

yang mempunyai kelemahan itu kemudian distandarisasi atau dibakukan

sehingga tingkat kepercayaannya lebih atau dapat dipertanggung

jawabkan,maka dalam dunia statistik deviasi standar sering digunakan.

Rumus standar deviasi adalah:

SD=

Keterangan :

SD= deviasi standar atau standart deviation

= jumlah deviasi standar setelah dikuadratkan dari masing-masing

deviasi

N= number of cases

Contoh soal:

Tinggi

badan(X)

f

Deviasi

(x=X-Mx)

150

1

-15,8

249,64

155

1

-10,8

116,64

157

1

-8,8

77,44

160

1

-5,8

33,64

163

1

-2,8

7,84

167

1

1,2

1,44

172

1

6,2

38,44

176

1

10,2

104,04

178

1

12,2

148,84

180

1

14,2

201,64

1658

10=N

0=

979,6=

5

JAWAB:

a.

Mencari meannya dengan :

Mx=

=

=165,8

b.

Mencari deviasi masing-masing nilai (x) dengan rumus x=X-Mx

(lihat kolom 3)

c.

Mengkuadratkan masing-masing deviasi yang sudah didapat pada langkah 2,

menjadi

, kemudian menjumlahkan

menjadi

= 979,6

d.

Mencari standar deviasi dengan rumus:

SD=

=

= 97.96

3.3JANGKAUAN KUARTIL

Kuartil adalah suatu harga yang membagi histogram frekuensi menjadi 4

bagian yang sama, sehingga disini akan terdapat 3 harga kuartil yaitu kuartil I

( K1), kuartil II (K2) dan kuartil III (K3), dimana harga kuarti II sama dengan

harga median.

Jangkauan kuartil disebut juga simpangan kuartil atau rentang semi antar

kuartil atau deviasi kuartil.

Kuartil dibagi menjadi 3 yaitu:

a.

Kuartil pertama ialah nilai dalam distribusi yang membatasi 25% frekuansi di

bagian bawah distribusi yang membatasi 25% frekuensi dibagian atas dan 75%

frekuensi dibagian bawah destribusi

b.

Kuartil kedua ialah nilai dalm distribusi yang membatasi 50% frekuensi

6

c.

Kuartil ketiga ialah nilai dalam distribusi yang membatasi 75% frekuensi di

bagian atas dan 25% frekuensi bagian bawah

Untuk kelompok data dimana n ≥ 100, dapat ditentukan 99 nilai, P

1

, P

2

, …

P

99

, yang disebut persentil pertama, kedua dan ke-99, yang membagi kelompok

data tersebut menjadi 100 bagian,masing-masing mempunyai bagian dengan

jumlah observasi yang sama, dan sedemikian rupa sehingga 1% data/observasi

sama atau lebih kecil dari P

1

, 2% data/observasi sama atau lebih kecil dari P

2.

Jangkauan kuartil

dirumuskan dengan:

JK=

(Q

₃

-Q

₁

)

Contoh:

Nilai

f

21-26

15

27-32

10

33-38

15

39-44

20

45-50

16

51-56

14

57-62

10

=100

Ditanya: nilai jangkauan kuartil?

7

Jawab :

=26,5+6

=38,5+6

=26,5+6

=38,5+6

=26.5+

=38,5+ 13,8

=26,5+4 =52,3

=30,5

JK=

(Q₃-Q₁)

=

(52,3 - 30,5)

=

(21,8)

= 10,9

8

3.4JANGKAUAN PERSENTIL

Bagian rumus yang berubah hanyalah bagian yang menentukan letak titik

persentil, dan bagian-bagian yang lain nya yang menyesuaikan persentil yang di

maksud.

Tabel

Letak Beberapa Titik Persentil

Persentil ke-1 n/100

Persentil ke-12 12n/100

Persentil ke-27 27n/100

persentil ke-87 87n/100

Persentil ke-99 99n/100

Jangkauan Persentil

dirumuskan dengan:

JP

₁₀₋₉₀

= P

₉₀

- P

₁₀

Dengan:

P₁₀ = persetil kesepuluh

P₉₀ = persentil kesembilanpuluh

Contoh:

JP

₂₀₋₈₀

= JP

₈₀

- JP

₂₀

9

BAB IV

PENUTUP

4.1 KESIMPULAN

Dari data di atas kita bisa menyimpulkan bahwa Statistika Deskriptif

masih berkaitan dengan pelajaran matematika , contohnya ukuran penyebaran

data . Ukuran penyebaran data bisa dibilang hampir mirip dengan matematika

hanya saja ukuran penyebaran data lebih mendalam di banding matematika .

4.2 SARAN

Kegiatan pratikum tentang Statistika Deskriptif hendaknya dapat

dilakukan dengan lebih cermat . Melakukan penghitung ukuran penyebaran data

di butuhkan kesabaran dan juga ketelitian .

Penyebaran Data

Pengertian Ukuran Penyebaran Data

Ukuran Penyebaran Data adalah suatu ukuran baik parameter atau

statistika untuk mengetahui seberapa besar penyimpangan data dengan nilai rata-rata hitungnya.Melalui ukuran penyebaran dapat diketahui seberapa jauh data-data menyebar dari titik pemusatannya atau suatu kelompok data terhadap pusat.Ukuran ini kadang-kadang dinamakan pula ukuran variasi yang

menggambarkan berpencarnya data kuantitatif.

Ukuran Penyebaran Data mencakup data : 1. Ungroup Data

Merupakan data yang belum dikelompokan atau bisa disebut data tunggal 2. Group Data

Merupakan data yang telah dikelompkkna biasanya berupa tabel distribusi frekuensi.

2.3 Macam-macam Ukuran Penyebaran Data

Beberapa Ukuran Penyebaran data yang terkenal meliputi sebagai berikut : 1. Jangkauan ( Range )

2. Simpangan Rata-rata ( Mean Deviation )

3. Variasi ( Variance )

4. Simpangan Baku ( Standard Deviation )

5. Simpangan Kuartil ( Quartil Deviation )

6. Jangkauan ( Persentil )

Pengertian dan Perhitungan Ukuran Penyebaran

Data

Jangkauan ( Range )

Jangkaun (Range) menyatakan ukuran yang menunjukan selisih nilai antara nilai maksimum dan nilai minimum atau selisih dari bilangan terbesar dengan bilangan terkecil.

Jangkauan (Range) merupakan ukuran penyebaran yang sangat kasar,sebab hanya bersangkutan dengan bilangan terbesar dan terkecil.Semakin kecil nilai Jangkauan (Range) maka kualitas data akan semakin baik,dan sebaliknya semakin besar nilai Jangkauan (Range),maka kualitas data semakin tidak baik.

Contoh Soal :

Kelas

K.A.

Rata-rata

Nilai IPK

11.2A.11

3,58

11.2B.11

3,05

11.2C.11

3,00

Jawab:

Jangkauan (Range) = 3,58 – 3,00

Jangkauan (Range) = Nilai Maks –

Nilai Min

= 0,58

Simpangan Rata-rata (Mean Deviation)

Simpangan Rata-rata (Mean Deviation) merupakan jumlah nilai mutlak dari selisih semua nilai dengan niali rata-rata dan dibagi banyaknya data.

Keterangan : Y = Nilai data

Ȳ = Nilai rata-rata N = Jumlah data

Contoh Soal :

Nilai UTS akuntansi dari 5 mahasiswa Komputerisasi Akuntansi adalah 9,6,7,8,5.Tentukan simpangan rata-rata !

Nilai Mahasiswa Y - Ȳ Nilai Mutlak

5 -2 2 6 -1 1 7 0 0 8 1 1 9 2 2

Simpangan Rata-rata = Σ

|

Y - Ȳ|

Data Tunggal

N

Total 35 6 Rata-rata Ȳ 7

Jawab:

Rata-rata Ȳ = ( 5 + 6 + 7 + 8 + 9 ) = 35 = 7

5 5

Simpangan Rata-rata = |5-7| + |6-7| + |7-7| + |8-7|+ |9-7|

Data Tunggal 5

= 2 + 1+ 0 + 1+ 2 = 6

= 1,2

5

Keterangan : Y = Nilai data Ȳ = Nilai rata-rata N = Jumlah data f = Frekuensi

Contoh Soal:

Tentukan Simpangan Rata-rata dari data berikut :

Nilai UTS SIM Frekuensi Nilai Tengah (Y) 4 --- 6 36 5

Simpangan Rata-rata = Σ

f

|

Y - Ȳ|

DataKelompok

N

7 --- 9 44 8

Jumlah 80

Jawab:

Nilai UTS Frekuens i (Y) Ʃf . Y | Y - Ȳ | Ʃf . | Y - Ȳ | 4 – 6 36 5 36 x 5 = 180 1,65 59,4 7 -- 9 44 8 44 x 8 = 352 1,35 59,4 Jumlah 80 532 118,8

Ȳ = Ʃ f . Y = 532 Simpangan Rata-rata = Ʃ f | Y - Ȳ

|

N 80 Data Kelompok N

= 6,65 = 118,8

80

= 1,485

Varisi (Variance)

Variasi (Variance) merupakan rata-rata kuadrat selisih atau simpangan dari semua nilai data terhadap rata-rata hitung.

Variansi ( S²) =

Σ

| Y

- Ȳ |²

Data Tunggal

N

Keterangan : Y = N ilai data Ȳ = Nilai rata- rata N = Jumlah data

Contoh Soal:

Nilai UTS akuntansi dari 5 mahasiswa Komputerisasi Akuntansi adalah 9,6,7,8,5.Tentukan Variansi !

Jawab :

Rata- rata Ȳ = ( 5 + 6 + 7 + 8 + 9 ) = 35 = 7

5 5

Variansi (S²) = |5-7|² + |6-7|² + |7-7|² + |8-7|² + |9-7|²

Data Tunggal 5

= -2² + -1²+ 0² + 1²+ 2 ²= 10

= 2

5 5

Variansi ( S² ) = Σ

f

|

Y - Ȳ |²

Data Kelompok N

Keterangan : Y = Nilai data Ȳ = Nilai rata- rata N = Jumlah data f = Frekuensi

Contoh :

Tentukan Variansi dari data berikut :

Nilai UTS SIM Frekuensi Nilai Tengah ( Y ) 4 --- 6 36 5 7 --- 9 44 8 Jumlah 80

Jawab :

Nilai UTS Frekue nsi ( Y) Σ f . Y | Y - Ȳ |² Σ f. | Y - Ȳ |² 4 – 6 36 5 36 x 5 =180 (5 - 6,65) ²=2,7225 98,01 7 – 9 44 8 44 x 8 =352 (8 – 6,65) ²=1,8225 80,19 Jumla h 80 532 178,2

Ȳ = Ʃ f . Y = 532 Variansi = Ʃ f | Y - Ȳ |

²

N 80 Data Kelompok N

= 6,65 = 178,2

80

= 2,2275

Simpangan Baku (Standard Deviation)

Simpangan Baku (Standard Deviation) merupakan akar kuadrat dari variansi dan menunjukan standar penyimpangan data terhadap nilai rata-ratanya.

Simpangan Baku =



Variansi (S²) atau



Σ

| Y

-

Ȳ |²

Data Tunggal



N

Keterangan : Y = Nilai data Ȳ = Nilai rata-rata N = Jumlah data

Contoh :

Nilai UTS akuntansi dari 5 mahasiswa Komputerisasi

Akuntansi adalah 9,6,7,8,5.Tentukan simpangan baku !

Jawab :

Rata-rata Ȳ = ( 5 + 6 + 7 + 8 + 9 ) = 35 = 7

5 5

Variansi (S²) = |5-7|² + |6-7|² + |7-7|² + |8-7|² + |9-7|²

Data Tunggal 5

= -2² + -1²+ 0² + 1²+ 2 ²= 10

= 2

5 5

Simpangan Baku =



Variansi (S²)

Data Tunggal =



2

Simpangan Baku =



Σ

f

| Y

- Ȳ |²

Data Kelompok



N

Keterangan : Y = Nilai data Ȳ = Nilai data N = Jumlah data f = Frekuensi

Contoh :

Tentukan Simpangan Baku dari data berikut :

Nilai UTS SIM

Frekuensi Nilai Tengah (Y) 4 – 6 36 5 7 -- 9 44 8 Jumlah 80

Jawab :

Nilai UTS Frekue nsi ( Y ) Σ f . Y | Y - Ȳ |² Σ f. | Y - Ȳ |² 4 – 6 36 5 36 x 5 =180 (5 - 6,65) ²=2,7225 98,01 7 – 9 44 8 44 x 8 =352 (8 – 6,65) ²=1,8225 80,19 Jumlah 80 532 178,2

Ȳ = Ʃ f . Y = 532 Variansi = Ʃ f | Y - Ȳ |

²

N 80 Data Kelompok N

= 6,65 = 178,2

80

Simpangan Baku =



Variansi (S²) = 2,2275

Data Kelompok =



2,2275

Simpangan Kuartil (Quartil Deviation)

Simpangan Kuartil (Quartil Deviation) merupakan rentang atau jarak semi antar kuartil.

Simpangan Kuartil = 1

( Q3 – Q1 )

Data Tunggal 2

Keterangan : Q1 = Kuarti Atas Q2 = Kuartil Tengah Q3 = Kuartil Bawah

Contoh Soal:

Diketahui data 3,6,2,6,7,5,4,3,8,2,5.Tentukan Simpangan Kuartil !

Jawab :

2,2,

3

,3,4,

5

,5,6,

6

,7,8

Simpangan Kuartil

=1/2( 6 – 3)

Data

Tunggal = 1,5

Simpangan Kuartil = 1

( Q3 – Q1 )

Data Kelompok 2

Keterangan : Q1 = Kuarti Atas Q2 = Kuartil Tengah Q3 = Kuartil Bawah

Contoh :

Tentukan Simpangan Kuartil.Dari data berikut !

Nilai Frekue nsi 57 --- 61 3 62 --- 66 5 67 --- 71 10

72 --- 76 12 77 – 81 10 82 – 86 8 Jumlah (n) 48

Jawab :

Untuk menentukan Q1 kita perlu ¼ x 48 =12,jadi Q1 terletak pada b=67-0,5 = 66,5; p= 5;F =8 ;f = 10.

Nilai Q1 = 66,5+ 12 – 8 . 5

10 = 66,5 + 2 = 68,5

Untuk menentukan Q1 kita perlu ¾ x 48 =36,jadi Q1 terletatk pada b=77-0,5 = 76,5;p= 5;F = 28;f = 10. Nilai Q3 = 76,5 + 36 – 28 . 5 10 = 76,5 + 4 = 80,5 Jadi,Simpangan Kuartil = ½ ( Q3 – Q1 ) = ½ ( 80,5 – 68,5 ) = ½ .12 = 6

Jangkauan Persentil

Jangkaun Persentil merupakan nilai yang membagi bilangan tersebut atas 100 bagian yang sama banyaknya setelah bilangan bilangan tersebut diurutkan dari yang terkecil sampai yang terbesar.

Jangkauan Persentil = Letak P

i

= data

ke i ( N + 1 )

100

Keterangan : N = Jumlah data i = Persentil ke -

Contoh :

Diketahui data : 9,3,8,4,5,6,8,7,5,7 Tentukan P20 dan P70!

Jawab :

Data diurutkan : 3 ,4, 5, 5, 6, 7, 7 ,8, 8, 9

Letak P20 = data ke 20 (10 + 1) = data ke 2 1/5

100 Nilai P20 = data ke 2 + 1 (data ke 3 – data ke2)

5

= 4 + 1/5 (5 – 4) = 4 1/5

JP 20 –70 = P70

-- P20

Letak P70 = data ke 70 ( 10 + 1) = data ke 7 7/10

100

Nilai P70 = data ke 7 + 7 (data ke 8 - data ke7)

10 = 7 + 7/10 ( 8 – 7 ) = 7 7/10 Jawab : JP 20 – 70 = P70 – P20 = 7 7/10 – 4 1/5 = 77/10 – 42/10 = 35/10 = 3 1/2

Mencari Ilmu

Selasa, 20 Mei 2014

Makalah Ukuran Penyebaran Data (Darman)

BAB I

PENDAHULUAN A. Latar belakang

Ukuran penyebaran data merupakan salah satu materi statistika yang didalamnya dibahas tentang sejauh mana data itu menyebar dari nilai rata-rata dalam data. Sebenarnya materi ini cukup mudah untuk kta pahami namun dalam menentukan nilai-nilai dari setiap komponen yang termasuk dalam ukuran

penyebaran data seringkali kita beleum mampu memhami ataupun kita keliru dalam mentukan nilai-nilai dari komponen-komponen tersebut.

B. Tujuan

 Memahami materi ukuran penyebaran data serta mampu menentukan nilai-nilai

dari komponen ukuran penebaran data.



Bagaiman kita memahami seperti apa ukuran penyebaran data ?



Apa saja yang termasuk dalam ukuran penyebaran data ?



Bagaimana kita menentukan nilai-nilai dari komponen ukuran penyebaran

data ?

D. Manfaat Penulisan

 Untuk dijadikan pegangan dalam pembelajaran statistika khususnya dalam

materi ukuran penyebaran data

BAB II

PEMBAHASAN

A. Ukuran Penyebaran Data

Dengan menentukan pemusatan data dan ukuran letak data ternyata belum cukup untuk memberikan gambaran yang jelas dari suatu data. Mengapa demikian? Untuk mengetahuinya, simaklah permasalahan berikut dengan

cermat! Dinas pertanian menyarankan penggunaan pupuk jenis baru dengan merk A dan B agar dapat meningkatkan hasil panen jagung. Setelah dilakukan uji coba pada 8 petak lahan yang sama, hasil panen jagung disajikan dalam tabel berikut.

Tabel 1.Data hasil panen jagung dalam ton Pupuk A 8 8 6 5 4 9 5 7 Pupuk B 6 6 7 7 8 7 6 5

Dari data tabel diatas rata–rata hasil panen dengan pupuk A dan pupuk B sama, yaitu 6,5 ton. Namun, apabila data tersebut digunakan untuk mengukur kualitas pupuk setiap lahan. Apakah kualitas pupuk A akan sama dengan pupuk B? Belum tentu. Coba Anda perhatikan tabel 1.20, hasil panen pupuk B memiliki rentang yang lebih kecil dari pupuk A, yaitu 5 sampai 8. Jadi, dengan

menggunakan pupuk B, hasil panen setiap petak lebih seimbang. Dengan demikian, untuk memberikan gambaran suatu data yang lebih lengkap diperlukan suatu ukuran, yaitu ukuran penyebaran data.

Sehingga dapat disimpulkan bahwa :

Ukuran penyebaran data adalah ukuran yang menunjukkan seberapa jauh data suatu menyebar dari rata–ratanya.

Beberapa ukuran penyebaran sebagai berikut.

1. Jangkauan

sering disebut range atau rentang. Jangkauan dari suatu data

didefinisikan sebagai selisih antara data terbesar dengan data terkecil. Untuk memahaminya, perhatikan contoh di bawah ini!

Contoh 1

Data terurut dari banyaknya buku pelajaran yang dimiliki 9 siswa yaitu: 4, 5, 6, 6, 7, 7, 7, 8, 9

Jangkauan data di atas adalah R = xmaks – x min = x9 – x1 = 9 – 4 = 5

Dapat disimpulkan bahwa untuk menentukan jangkauan suatu kumpulan data tunggal dapat menggunakan persamaan:

kumpulan data tunggal dapat menggunakan persamaan:

R = xmaks– xmin

Keterangan:

R = jangkauan/range/rentang

Xmaks = data terbesar

Xmin = data terkecil

Jangkauan data berkelompok merupakan selisih antara nilai tengah kelas terakhir dengan nilai tengah kelas pertama.

Perhatikan tabel berikut ini!

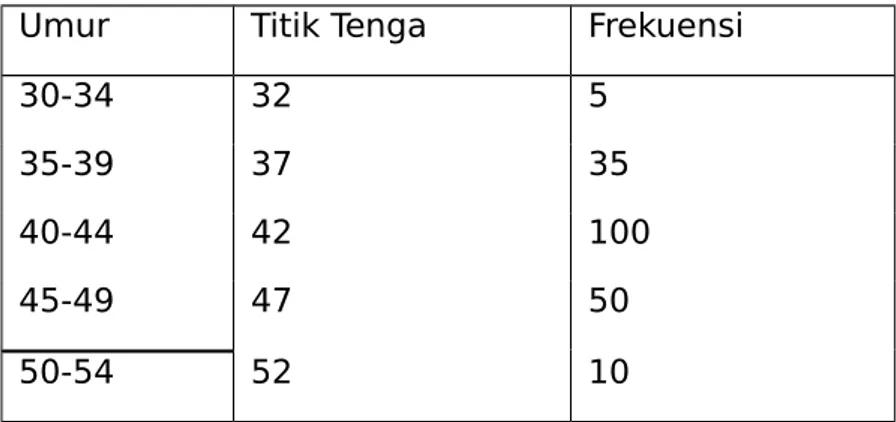
Tabel 2 Data umur peserta sertifikasi guru

Umur Titik Tenga Frekuensi

30-34 32 5

35-39 37 35

40-44 42 100

45-49 47 50

50-54 52 10

Tabel 2 menunjukkan data umur peserta yang mengikuti diklat sertifikasi guru yang berjumlah 200 orang.

Bila nilai tengah kelas pertama adalah 32 dan nilai tengah kelas terakhir adalah 52, maka

R = 52 – 32 = 20

Jadi, jangkauan data dari tabel 2 adalah 20. Dapat disimpulkan bahwa untuk menentukan jangkauan data berkelompok digunakan persamaan:

R = xmaks– xmin

R = jangkauan/range/rentang

Xmin = nilai tengah kelas pertama

2. Jangkauan Antarkuartil

Jangkauan antarkuartil juga disebut hamparan. Bagaimana cara

menentukan jangkauan antarkuartil ? Perhatikan contoh pada subbab jangkauan untuk data tunggal. Diperoleh nilai kuartil pertama Q1 = 5,5 dan kuartil ketiga Q3

= 7,5.

Jadi, jangkauan antarkuartilnya adalah H = 7,5 – 5,5 = 2.

Dapat disimpulkan bahwa:

Jangkauan antarkuartil adalah selisih antara kuartil ketiga dengan kuartil pertama.

Untuk menentukan jangkauan antarkuartil, dapat digunakan persamaan:

H = Q3 – Q1

Keterangan:

H = jangkauan antarkuartil (hamparan)

Q3 = kuartil ketiga

Q1 = kuartil pertama

3. Jangkauan semi antarkuartil

Jangkauan semi antarkuartil juga disebut simpangan kuartil. Apa

Untuk mengetahuinya, perhatikan contoh 1.7. Diperoleh nilai jangkauan antarkuartil H = 2, nilai jangkauan semi antarkuartilnya adalah

Dapat disimpulkan bahwa:

Jangkauan semi antarkuartil adalah nilai dari setengah kali jangkauan antarkuartil.

Pengertian di atas dapat dinyatakan dalam persamaan:

Keterangan:

Qd = jangkauan semi antarkuartil

H = jangkauan antarkuartil (hamparan)

4. Langkah

Apabila nilai jangkauan antarkuartilnya dikalikan satu setengah, maka diperoleh langkah sebesar:

L = 1

Jadi, dapat disimpulkan bahwa:

Langkah adalah nilai dari satusetengah dikalikan jangkauan antarkuartil.

Pengertian tersebut dapat ditunjukkan dengan persamaan:

L = 1 =

5. Pagar Dalam dan Pagar Luar

Untuk menentukan pagar dalam dan pagar luar, coba Anda lihat kembali hasil pada contoh sebelumnya. Apakah ada hubungannya?

Bila diperoleh, pagar dalam = Q1 – L = 5,5 – 3 = 2,5 pagar luar = Q3 + L = 7,5 + 3 = 10,5 Dapat disimpulkan bahwa untuk menentukan pagar dalam dan luar digunakan persamaan:

Pagar dalam = Q1 – L

Pagar luar = Q3 + L

Sehingga dapat didefinisikan:

Pagar dalam adalah nilai data yang berada satu langkah di bawah kuartil pertama.

Pagar luar adalah nilai data yang berada satu langkah di atas kuarti ketiga.

Pagar dalam dan pagar luar berfungsi sebagai batas penentu normal atau tidaknya suatu data.

Data xi dikatakan normal apabila nilai data yang satu dengan nilai data yang lain tidak jauh berbeda dan terletak di antara batas–batas pagar dalam dan pagar luar.

Data xi dikatakan tidak normal apabila nilai data tersebut tidak konsisten dalam kelompoknya, dan terletak kurang dari pagar dalam dan lebih dari pagar luar.

Data yang tidak konsisten dalam kelompoknya disebut pancilan atau data liar. Pencilan pada suatu kumpulan data menimbulkan kecurigaan sehingga pencilan itu perlu dikaji secara seksama. Apa yang menjadi penyebabnya? Munculnya data pencilan dalam suatu kumpulan data dapat terjadi akibat kesalahan ketika mencatat data dan juga kesalahan ketika melakukan pengukuran.

6. Statistik Lima Serangkai

Nilai–nilai statistik seperti jangkauan, jangkauan antarkuartil, jangkauan semi antarkuartil, langkah, pagar dalam, dan pagar luar akan lebih mudah ditentukan apabila kumpulan data disajikan dengan menggunakan statistik lima serangkai dalam bentuk bagan.

Untuk lebih jelasnya, perhatikan contoh berikut. Contoh 2

Diketahui data 31, 32, 27, 28, 29, 36, 35, 32, 34, tentukanlah: a. Statistik lima serangkai

b. Jangkauan

c. Jangkauan antarkuartil d. Jangkauan semi antarkuartil e. Langkah

f. Pagar dalam dan pagar luar

g. Jika terdapat nilai 10 dan 50, apakah kedua nilai data tersebut konsisten dalam kumpulan data yang sudah diketahui?

Jawab:

a. Statistik lima serangkai

* Urutkan data dari data yang terkecil hingga yang terbesar membentuk statistik jajaran, sebagai berikut:

27, 28, 29, 31, 32, 32, 34, 35, 36, 37, 38

Tentukan kuartil dengan mencari letak Q1, Q2, dan Q3.

Letak Q1 = = data ke–3, yaitu Q1 = = 29

Letak Q2 = = data ke–6, yaitu Q2 = = 32

Letak Q3 = = data ke–9, yaitu Q3 = x9 = 36

Jadi, statistik lima serangkai dapat disajikan pada tabel berikut.

xmin = 27 Xmax = 38

b. Jangkauan

R = xmaks– xmin

= 38 – 27 = 11

Jadi, jangkauan dari data adalah 11.

c. Jangkauan antarkuartil

H = Q3 – Q1

= 7

Jadi, jangkauan antarkuartil dari data adalah 7.

d. Jangkauan semi antarkuartil,

= 3,5

Jadi, jangkauan semi antarkuartil dari data adalah 3,5.

e. Langkah, L = 1,5 H

7= 1,5 × = 10,5

Jadi, langkah dari data adalah 10,5.

f. Pagar dalam = Q1 – L = 29 – 10,5 = 18,5 Pagar luar = Q3 + L = 36,5 + 10,5 = 46,5

g. Karena 10 lebih kecil dari pagar dalam dan 50 lebih besar dari pagar luar, nilai data 10 dan 50 tidak konsisten terhadap kumpulan data pada soal tersebut.

Menetukan Nilai statistik Lima Serangkai dalam tabel distribusi frekuensi

7. Simpangan Rata–Rata

Pada subbab terdahulu, Anda telah mempelajari nilai mean atau rata– rata hitung dari kumpulan data. Bagaimanakah hubungan ukuran penyebaran data terhadap rata–rata data tersebut? Untuk mengetahuinya, marilah kita simak contoh 3 berikut ini.

Diketahui hasil dari pengukuran adalah 3, 4, 5, 6, 8, 9. Penyebaran nilai data terhadap rata–ratanya dapat ditentukan dengan langkah– langkah berikut.

a. Sebelumnya, Anda menentukan terlebih dahulu nilai rata–rata dari data dengan n = 5, yaitu:

b. Tuangkan data-data tersebut dalam tabel. Tabel 3 3 -3 3 4 -2 2 6 0 0 8 2 2 9 3 3

c. Selanjutnya dari tabel tersebut, simpangan rata–rata data dapat diperoleh dengan persamaan:

Jadi, simpangan rata–rata data tersebut adalah 2. Dari contoh di atas, dapat disimpulkan bahwa:

Simpangan rata–rata atau deviasi rata–rata adalah ukuran yang menyatakan seberapa besar penyebaran tiap nilai data terhadap nilai meannya (rata– ratanya).

Bila diketahui data tunggal , , , ..., dengan rata–rata maka simpangan dari adalah , simpangan dari adalah , dan seterusnya sehingga diperoleh jumlah nilai mutlak simpangan, yaitu:

Simpangan rata–rata dapat didefinisikan sebagai: Keterangan : SR = simpangan rata-rata n =banyaknya data = data ke-i i= 1, 2, 3, …,n = mean

Untuk data dari tabel distribusi frekuensi, simpangan rata–rata dapat ditentukan dengan persamaan:

Keterangan :

SR = simpangan rata-rata = frekuensi data ke-i n =banyaknya data = data ke-i

i= 1, 2, 3, …,n

= mean

Untuk memahaminya perhatikan contoh berikut ini! Contoh 4

Data pengukuran berat masing–masing barang elektronik bila akan ditentukan simpangan rata–ratanya, maka tabel menjadi:

Berat(kg )

Titik tenga frekuensi

11-15 13 1 13 -16 16 16-20 18 4 72 -11 11 21-25 23 8 184 -6 6 26-30 28 10 280 -1 1 31-35 33 9 297 4 4 36-40 38 6 228 9 9 41-45 43 2 86 14 14 Jumlah - 40 1160 236 Maka diperoleh = 5,9

Jadi, simpangan rata–rata data pada tabel 4 adalah 5,9.

8. Variansi dan Simpangan Baku

Ukuran penyebaran data yang paling sering digunakan adalah variansi (ragam) dan simpangan baku (standar deviasi). Ragam dan simpangan baku menjelaskan penyebaran data di sekitar rataan. Pada bagian ini, kita hanya akan membahas cara menghitung dan mendapatkan ragam dan simpangan baku dari suatu data, sedangkan kegunaannya belum akan dipelajari pada bab ini.

a. Variansi (Ragam)

Coba Anda ingat kembali cara menentukan nilai mean atau rata– rata hitung dari suatu data. Mean atau rata–rata hitung mewakili suatu data sehingga dalam pengamatan diharapkan nilai data lebih kecil dari nilai rata–rata.

Untuk memahaminya, perhatikan nilai–nilai berikut: 1, 4, 8, 10, 12. Rata– rata data tersebut ( ) adalah 7 dan simpangan dari masing– masing data ( – )

adalah –6, –3, 1, 3, 5. Bila Anda perhatikan, jumlah dari simpangan di atas adalah nol.

Misalnya, kumpulan data , , ..., mempunyai rata–rata , maka simpangan masing–masing data dari rata–ratanya adalah ( ), (),

..., (). Jumlah dari semua simpangan :

Harus sama dengan nol. Untuk mengatasi hal itu, diperlukan suatu ukuran penyebaran, yaitu variansi (ragam). Variansi didasarkan pada jumlah kuadrat dari simpangan, didefinisikan sebagai:

Variansi (ragam) adalah rata–rata dari jumlah kuadrat simpangan tiap data.

Persamaan berikut digunakan untuk menentukan besarnya variansi (ragam).

Keterangan :

= variansi/ragam

Maka, nilai variansi/ragam dari data pada contoh di atas adalah:

Jadi, variansi dari data adalah 16.

Untuk data berkelompok atau data yang disajikan dalam tabel distribusi frekuensi, variansi atau ragam dapat dinyatakan dengan persamaan:

Untuk memahami penggunaannya, perhatikan contoh berikut ini! Dari data pada tabel 5 diperoleh data mengenai berat barang elektronik. Variansi/ragam dari data tersebut dapat ditentukan, yaitu dengan mengkuadratkan simpangannya. Bila rata–rata data = 29,

maka:

Tabel 5 Berat barang elektronik dalam (kg) Berat(kg

)

Titik tenga ) frekuensi

11-15 13 1 -16 256 256 16-20 18 4 -11 121 484 21-25 23 8 -6 36 283 26-30 28 10 -1 1 10 31-35 33 9 4 16 144 36-40 38 6 9 81 486 41-45 43 2 14 196 392 Jumlah - 40 - - 2060 Maka diperoleh:

Jadi, variansi atau ragam data pada tabel adalah 51,5.

b. Simpangan Baku (Standar Deviasi)

Untuk mengatasi kesulitan menafsirkan ukuran penyebaran data yang dinyatakan dalam satuan kuadrat yaitu variansi (ragam), digunakan suatu ukuran yang disebut simpangan baku atau standar deviasi. Simpangan baku mengukur penyebaran data dengan satuan yang sama dengan satuan data.

Bila satuan kuadrat merupakan bentuk variansi atau ragam, apa

hubungan variansi dengan simpangan baku? Untuk mengetahuinya, simaklah contoh berikut ini.

Data dari tabel 5 diperoleh nilai variansi atau ragam, yaitu: simpangan bakunya adalah:

s = = = 7,18

Jadi, nilai simpangan bakunya adalah 7,18.

Sehingga dapat disimpulkan bahwa:

Simpangan baku atau standar deviasi adalah nilai akar dari variansi atau ragam.

Simpangan baku/standar deviasi dapat dihitung dengan persamaan: 1) Untuk data tunggal

2) Untuk data berkelompok

dengan s = simpangan baku/standar deviasi