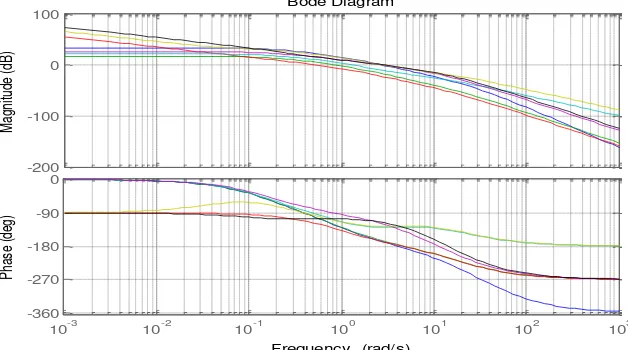
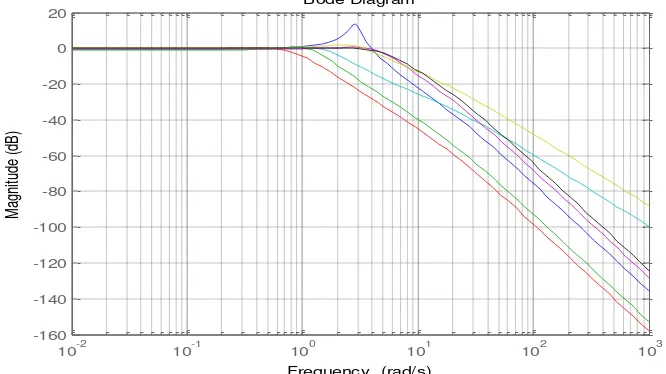
04 Perancangan dan Analisa Kendali Sistem Eksitasi Generator Tipe Arus Searah
Teks penuh
Gambar


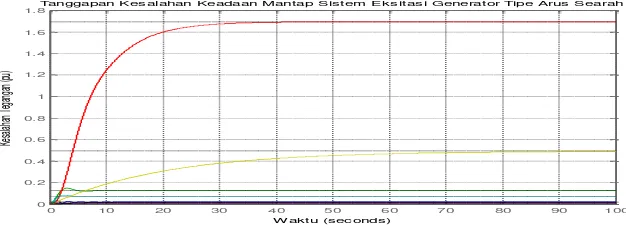
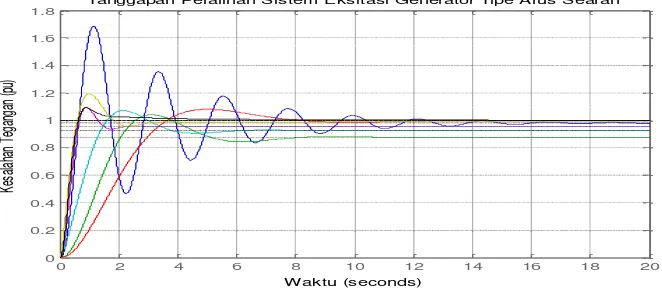
Dokumen terkait
Dalam kompetisi itu, aktor- aktor politik (politisi dan partai politik) bertemu, bersentuhan dan membangun jejaring dengan aktor lain, seperti masyarakat sipil dan
Dengan melihat kemampuan yang dimiliki oleh algoritma K-NN dalam proses klasifikasi, dan Transformasi Kosinus Diskrit dalam pengolahan sinyal untuk keperluan
Kemudian pada layar utama terdapat tombol ‘Show Original Image’ yang berfungsi untuk menampilkan kembali gambar asli image yang sudah di-load sebelumnya, Tujuan dari
Sedangkan pengertian Konsumen Menurut pengertian Pasal 1 angka 2 UU PK, “Konsumen adalah setiap orang pemakai barang dan/atau jasa yang tersedia dalam masyarakat, baik
Apa yang dapat kita lakukan (bagaimana organisasi akan menterjemahkan keinginan pelanggan pada atribut-atribut produk dan proses serta sasaran desain. Nilai-nilai dengan
keterampilan duru dan peserta didik melalui pembinaan untuk guru dan peserta didik dalam proses belajar mengajar dan memberikan sertivikasi guru dalam upaya meningkatkan
Sebelum melakukan pengamatan, diatur posisi sinyal pada mode X-Y dengan menekan tombol GND pada kedua kanal masukan hingga terlihat 1 titik
(4) Guru yang belum memiliki ijazah Sarjana (S1)/Diploma IV yang sudah memiliki pangkat Penata Muda Tingkat I golongan ruang III/b ke atas, apabila memperoleh