Penentuan Titik-Titik Batas Optimum Strata pada Penarikan Contoh Acak Berlapis dengan Pemograman Dinamik (Kasus : Pengeluaran per Kapita Provinsi Jawa Timur Tahun 2008) Mahyudi
Teks penuh
Gambar
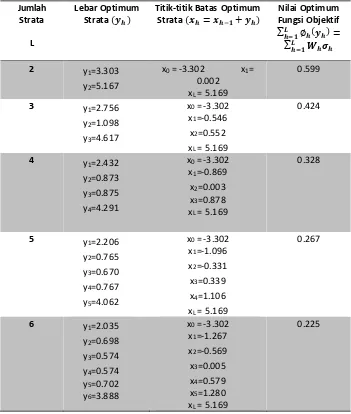
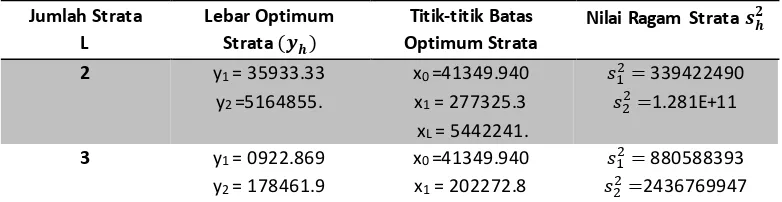
Dokumen terkait
Berdasarkan survey yang telah dilakukan peneliti cukup mewakili dari delapan item model COPA juga merupakan faktor yang akan diteliti untuk mengetahui
Adakah terdapat perbezaan yang signifikan dalam peningkatan keupayaan mengingati konsep Sejarah dan pencapaian pelajar dalam kalangan murid yang mengikuti dan tidak
Kuala Lumpur ; kcrana sudi telah membenarkan saya memperolehi data - data yang berguna untuk kajian saya. iii)Knkitangan di Muhkamah SoaAion , Cik Hg yang Lelah
0,479. Dengan demikian dapat disimpulkan bahwa lingkungan kerja memiliki pengaruh paling dominan terhadap produktivitas kerja karyawan di PTPN XII Kebun Renteng
Sejak dari idiologi, struktur kepengurusan, dan keberadaan tokoh-tokoh gerwani yang sebagian besar merupakan keluarga Komunis, penjelasan buku ini justru mengukuhkan
Sasaran Keberhasilan Kegiatan Penyelenggara pelaksanaan Ujian Kompetensi Keahlian ditingkat satuan pendidikan dalam hal ini adalah SMK Gazza Wiguna tentu mengharapkan
pengukuran sifat feroelektrik didapatkan bahwa senyawa hasil sintesis dari oksida logam berstruktur Aurivillius tipe PBTW menunjukkan adanya pola histerisis.. Kata kunci : Oksida
Penelitian ini dilakukan untuk mengetahui prevalensi gejala depresi pada pasien skizofrenia paranoid di RSJ Soeharto Heerdjan Jakarta pada tahun 2010 berdasarkan