ii
KATA PENGANTAR
Puji dan syukur penulis panjatkan ke hadirat Allah SWT, karena atas limpahan rahmat dan karunianya berupa kesehatan dan pemikiran yang jernih, sehingga penulis dapat menyelesaikan tesis dengan judul “Penerapan Pembelajaran Berbasis Masalah (Problem Based Learning) Untuk Meningkatkan Kemampuan Berpikir Kritis Dan Komunikasi Matematis Siswa Sekolah Dasar.”
Tesis ini disusun dalam rangka memenuhi salah satu syarat untuk memperoleh gelar Magister Pendidikan pada Program Studi Pendidikan Dasar, Universitas Pendidikan Indonesia. Penelitian ini berfokus pada upaya mengungkapkan peningkatan kemampuan berpikir kritis dan kemampuan komunikasi matematis, sebagai akibat yang diberikan berupa perlakuan pembelajaran berbasis masalah dan pembelajaran konvensional.
Tesis ini terdiri dari lima bab. Bab I, terdiri dari latar belakang masalah, rumusan masalah, tujuan penelitian, definisi operasional, dan hipotesis penelitian. Bab II, Kajian pustaka, terdiri dari pembelajaran berbasis masalah, berpikir kritis, kemampuan komunikasi matematis, teori belajar pendukung, dan penelitian yang relevan. Bab III Metode penelitian, terdiri dari disain penelitian, subyek penelitian, dan teknik pengolahan data. Bab IV merupakan hasil penelitian dan pembahasan. Bab V memaparkan simpulan dan saran-saran dari hasil penelitian.
Demikian tesis ini disusun dengan harapan memberikan tambahan wawasan pengetahuan dalam pengembangan pembelajaran matematika, khususnya bagi guru sebagai upaya mengoptimalkan kemampuan matematika siswa. Kritik dan saran untuk perbaikan tesis ini sangat diharapkan dan dihargai dengan setinggi-tingginya.
iii
UCAPAN TERIMA KASIH
Penulis menyadari dan merasakan sepenuhnya bahwa dalam penyelesaian tesis ini tidak terlepas dari bantuan, bimbingan, dan dukungan dari berbagai pihak. Untuk itu penulis menyampaikan ucapan terima kasih dan penghargaan setulus-tulusnya kepada yang terhormat:
1. Bapak Prof. Dr.H. Didi Suryadi, M.Ed. selaku Pembimbing I yang di tengah-tengah kesibukannya telah memberikan bimbingan, arahan, dan nasihat serta selalu memberi motivasi dengan penuh kesabaran mulai dari awal sampai akhir penyusunan tesis ini.
2. Bapak Drs. Turmudi, M.Ed., M.Sc., Ph.D. selaku Pembimbing II yang selalu meluangkan waktu di tengah-tengah kesibukannya untuk memberikan bimbingan, arahan, nasihat, dan motivasi dengan penuh perhatian dan kesabaran sampai selesai penyusunan tesis ini.
3. Bapak Prof. Dr. H. Tatang Herman, M.Ed. selaku penguji yang telah memberikan banyak arahan serta motivasi
4. Bapak Dr. M. Solehuddin, M.Pd., M.A. selaku ketua Program Studi Pendidikan Dasar, yang selalu memotivasi penyelesaian studi secepatnya kepada setiap mahasiswa.
5. Kepala Sekolah dan Guru SDN 1 Makmur, SDN 5 Makmur, SD 6 Makmur, SD 7 Makmur, dan SD 10 Makmur yang telah memberikan izin, bantuan dan kemudahan kepada penulis selama melaksanakan penelitian di sekolah-sekolah tersebut.
iv
dorongan yang kalian berikan sejak mengikuti perkuliahan sampai penyelesaian tesis ini.
7. Teman-teman seperjuangan di Program Studi Pendidikan Dasar, khususnya buat Tim 18 yang merupakan dosen tetap di Universitas Almuslim Bireuen yang telah memberikan motivasi dan semua pihak yang tidak dapat disebutkan namanya satu persatu.
Akhirnya, atas segala budi baik dari semua pihak yang telah memberikan bantuan dan dorongan, baik moral maupun spiritual, penulis serahkan kepada Allah SWT semoga mendapat balasan yang berlipat ganda. Amin.
Bandung, Juni 2011 Penulis
v
PERNYATAAN
Dengan sesungguhnya saya, Fachrurazi, menyatakan bahwa tesis yang berjudul “Penerapan Pembelajaran Berbasis Masalah (Problem Based Learning) untuk Meningkatkan Kemampuan Berpikir Kritis dan Komunikasi Matematis Siswa Sekolah Dasar” adalah benar-benar karya asli saya melalui hasil penelitian dan saya tidak melakukan penjiplakan atau pengutipan dengan cara yang tidak sesuai dengan etika yang berlaku dalam masyarakat keilmuan.
Bandung, Juni 2011 Yang membuat Pernyataan,
vi A. Pembelajaran Berbasis Masalah ... 18
B. Kemampuan Berpikir Kritis ... 25
C. Kemampuan Komunikasi Matematis ... 32
D. Teori Belajar Pendukung ... 35
D. Pengembangan Instrumen Penelitian ... 47
E. Teknik Pengumpulan Data ... 60
F. Teknik Pengolahan Data ... 61
G. Teknik Analisis Data ... 62
H. Prosedur Penelitian ... 63
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. Hasil Penelitian ... 66
vii
2. Hasil Postes Kemampuan Berpikir Kritis dan
Kemampuan Komunikasi Matematis ... 74
3. Peningkatan Kemampuan Berpikir Kritis dan Komunikasi Matematis Berdasarkan Pembelajaran ... 79
4. Peningkatan Kemampuan Berpikir Kritis dan Komunikasi Menurut Level Sekolah ... 83
5. Aktivitas Guru dan Siswa Selama Proses Pembelajaran... 94
6. Sikap Siswa Terhadap Pembelajaran Matematika... 96
7. Tanggapan Guru terhadap Pembelajaran Berbasis Masalah ... 100
B. Pembahasan Hasil Penelitian ... 101
1. Pembelajaran Berbasis Masalah ... 101
2. Level Sekolah ... 108
3. Kemampuan Berpikir Kritis ... 110
4. Kemampuan Komunikasi Matematis ... 113
5. Sikap Siswa Terhadap Pembelajaran Berbasis Masalah ... 119
BAB V KESIMPULAN DAN SARAN A. Kesimpulan ... 121
B. Saran ... 122
DAFTAR PUSTAKA ... 125 DAFTAR LAMPIRAN
A. Alat Pengumpul Data B. Data Penelitian C. Foto-foto Penelitian D. Surat-surat
viii
DAFTAR TABEL
Tabel Halaman
2.1 Langkah-langkah Pembelajaran Berbasis Masalah ... 25
3.1 Analisis Materi Pelajaran ... 47
3.2 Kriteria Skor Kemampuan Berpikir Kritis ... 48
3.3 Pedoman Penskoran Tes Kemampuan Komunikasi Matematis ... 50
3.4 Model Pedagogi Pembelajaran ... 53
3.5 Analisis Validitas Tes Kemampuan Berpikir Kritis dan Kemampuan Komunikasi Matematis ... 56
3.6 Analisis Kesukaran Tes Kemampuan Berpikir Kritis dan Kemampuan Komunikasi Matematis ... 58
3.7 Analisis Daya Pembeda Tes Kemampuan Berpikir Kritis dan Kemampuan Komunikasi Matematis ... 59
3.8 Klasifikasi N-Gain ... 62
4.1 Korelasi Postes Kemampuan Berpikir Kritis Versi Peneliti dan Pembanding ... 67
4.2 Korelasi Postes Kemampuan Berpikir Kritis Versi Peneliti dan Pembanding ... 68
4.3 Deskripsi Hasil Pretes Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 70
4.4 Hasil Uji Normalitas Skor Pretes Kemampuan Berpikir Kritis dan Kemampuan Komunikasi ... 71
4.5 Uji Homogenitas Skor Pretes Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 72
4.6 Hasil Pengujian Perbedaan Rata-rata Skor Pretes Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 73
ix
4.8 Hasil Uji Normalitas Skor Postes Kemampuan Berpikir Kritis
dan Komunikasi Matematis ... 76
4.9 Uji Homogenitas Skor Postes Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 77
4.10 Hasil Pengujian Perbedaan Rata-rata Skor Postes Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 78
4.11 Rata-Rata N-Gain Kemampuan Berpikir Kritis ... 79
4.12 Hasil Uji Normalitas Peningkatan Kemampuan Berpikir Kritis ... 80
4.13 Uji Homogenitas Peningkatan Kemampuan Berpikir Kritis ... 80
4.14 Pengujian Perbedaan Rata-rata Peningkatan Kemampuan Berpikir Kritis ... 81
4.15 Rata-rata N-Gain Kemampuan Komunikasi Matematis ... 82
4.16 Hasil Uji Normalitas Peningkatan Kemampuan Komunikasi Matematis ... 83
4.17 Uji Homogenitas Peningkatan Kemampuan Komunikasi Matematis .. 84
4.18 Pengujian Perbedaan Rata-rata Peningkatan Kemampuan Komunikasi ... 84
4.19 Rerata dan Devisiasi Baku N-Gain Kemampuan Berpikir Kritis Siswa Berdasarkan Level Sekolah ... 85
4.20 Uji Anova Dua Jalur Kemampuan Berpikir Kritis Berdasarkan Level Sekolah ... 87
4.21 Hasil Uji t Pengaruh Model Pembelajaran Berdasarkan Level Sekolah terhadap Kemampuan Berpikir Kritis... 89
4.22 Rerata dan Devisiasi Baku N-Gain Kemampuan Komunikasi Matematis Siswa Berdasarkan Level Sekolah ... 90
4.23 Uji Anova Dua Jalur Kemampuan Komunikasi Matematis Berdasarkan Level Sekolah ... 91
4.24 Hasil Uji t Pengaruh Model Pembelajaran Berdasarkan Level Sekolah terhadap Kemampuan Komunikasi Matematis... 94
4.25 Hasil Perhitungan Data Observasi Tiap Pertemuan ... 96
x
DAFTAR GAMBAR
Gambar Halaman
3.1 Prosedur Penelitian ... 65 4.1 Diagram Batang Rata-rata Skor Pretes Kemampuan
Berpikir Kritis dan Komunikasi Matematis... 71 4.2 Diagram Batang Rata-rata Skor Postes Kemampuan
Berpikir Kritis dan Komunikasi Matematis... 75 4.3 Peningkatan Kemampuan Berpikir Kritis Menurut Level Sekolah ... 88 4.4 Peningkatan Kemampuan Komunikasi Matematis
xi
DAFTAR LAMPIRAN
Lampiran A Alat Pengumpul Data
3.1 Kisi-kisi Soal Tes kemampuan Berpikir Kritis dan
Komunikasi Matematis ... 130
3.2 Soal Pretes Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 132
3.3 Soal Postes Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 137
3.4 Hasil Uji Instrumen dengan Bantuan Program Anates Versi 4.0.5 ... 142
3.5 Lembar Observasi Aktivitas Siswa dalam Pembelajaran Matematika dengan Pembelajaran Berbasis Masalah ... 147
3.6 Lembar Observasi Aktivitas Guru dalam Pembelajaran Matematika dengan Pembelajaran Berbasis Masalah ... 148
3.7 Angket Skala Sikap Siswa terhadap Penerapan Model Pembelajaran Berbasis Masalah ... 149
3.8 Daftar Isian Guru... 150
3.9 Rencana Pelaksanaan Pembelajaran ... 152
3.10 Lembar Kegiatan Siswa ... 168
3.11 Kunci Jawaban Kemampuan Berpikir Kritis dan Komunikasi Matematis ... 192
Lampiran B Data Penelitian 4.1 Korelasi Pemeriksaan Soal Kemampuan Berpikir Kritis dan Komunikasi Matematis dengan Analisis SPSS Versi 17 ... 196
4.2 Skor Pretes Kemampuan Berpikir Kritis Kelas Eksperimen ... 201
4.3 Skor Pretes Kemampuan Berpikir Kritis Kelas Kontrol ... 202
4.4 Uji Normalitas Skor Pretes Kemampuan Berpikir Kritis ... 203
4.5 Uji Homogenitas Skor Pretes kemampuan Berpikir Kritis ... 204
4.6 Uji Beda Rata-rata Skor pretes Kemampuan Berpikir Kritis ... 205
xii
4.8 Skor Postes Kemampuan Berpikir Kritis Kelas Kontrol ... 207
4.9 Uji Normalitas Postes Kemampuan Berpikir Kritis ... 208
4.10 Uji Homogenitas Skor Postes Kemampuan Berpikir Kritis ... 209
4.11 Uji Beda Rata-rata Skor Postes Kemampuan Berpikir Kritis ... 210
4.12 Gain Ternormalisasi Kemampuan Berpikir Kritis Kelompok Eksperimen ... 211
4.13 Gain Ternormalisasi Kemampuan Berpikir Kritis Kelompok Eksperimen ... 212
4.14 Uji Normalitas Peningkatan Kemampuan Berpikir Kritis ... 213
4.15 Uji Homogenitas Peningkatan Kemampuan Berpikir Kritis ... 214
4.16 Uji Perbedaan Peningkatan Kemampuan Berpikir Kritis ... 215
4.17 Skor Pretes Kemampuan Komunikasi Matematis Kelas Eksperimen ... 216
4.18 Skor Pretes Kemampuan Komunikasi Matematis Kelas Kontrol ... 217
4.19 Uji Normalitas Skor Pretes Kemampuan Komunikasi Matematis ... 218
4.20 Uji Homogenitas Skor Pretes Kemampuan Komunikasi Matematis ... 219
4.21 Uji beda Rata-rata Skor Pretes Kemampuan Komunikasi Matematis ... 220
4.22 Skor Postes Kemampuan Komunikasi Matematis Kelas Eksperimen ... 221
4.23 Skor Postes Kemampuan Komunikasi Matematis Kelas Kontrol ... 222
4.24 Uji Normalitas Skor Postes Kemampuan Komunikasi Matematis ... 223
4.25 Uji Homogenitas Skor Postes Kemampuan Komunikasi Matematis ... 224
4.26 Uji Beda Rata-rata Skor Postes Kemampuan Komunikasi Matematis ... 225
4.27 Gain Ternormalisasi Kemampuan Komunikasi Matematis Kelompok Eksperimen ... 226
4.28 Gain Ternormalisasi Kemampuan Komunikasi Matematis Kelompok Kontrol ... 227
4.29 Uji Normalitas Peningkatan Kemampuan Komunikasi Matematis ... 228
4.30 Uji Homogenitas Peningkatan Kemampuan Komunikasi Matematis ... 229
4.31 Uji Beda Peningkatan Kemampuan Komunikasi Matematis ... 230
4.32 Uji Normalitas N-gain Kemampuan Berpikir Kritis Level Sekolah ... 231
xiii
Level Sekolah ... 234 4.35 Uji Beda Rata-rata Komunikasi Matematis Berdasarkan
Level Sekolah ... 235 4.36 Uji Anova Dua Jalur Kemampuan Berpikir Kritis ... 237 4.37 Uji Anova Dua Jalur Kemampuan Komunikasi Matematis ... 240 4.38 Hasil Observasi Aktivitas Siswa dalam Pembelajaran Berbasis Masalah
Level Sekolah Tinggi ... 243 4.39 Hasil Observasi Aktivitas Siswa dalam Pembelajaran Berbasis Masalah
Level Sekolah Sedang ... 244 4.40 Hasil Observasi Aktivitas Siswa dalam Pembelajaran Berbasis Masalah
Level Sekolah Rendah... 245 4.41 Hasil Observasi Kegiatan Guru Kelas Eksperimen
Level Sekolah Tinggi ... 246 4.42 Hasil Observasi Kegiatan Guru Kelas Eksperimen
Level Sekolah Sedang ... 247 4.43 Hasil Observasi Kegiatan Guru Kelas Eksperimen
Level Sekolah Rendah... 248 4.44 Data Hasil Angket Siswa Penerapan Model
Pembelajaran Berbasis Masalah ... 249 4.45 Frekuensi dan Persentase Jawaban Angket Sikap Siswa
Kelas Eksperimen... 251
Lampiran C Foto-foto Penelitian
1. Aktivitas siswa dalam PBM pada Sekolah Level Tinggi ... 252 2. Aktivitas siswa dalam PBM pada Sekolah Level Sedang ... 253 3. Aktivitas siswa dalam PBM pada Sekolah Level Rendah ... 254
1 BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Perubahan cepat dan pesat sering kali terjadi dalam berbagai bidang seperti pendidikan, politik, ekonomi, ilmu pengetahuan, teknologi, dan budaya. Hal ini memungkinkan semua pihak dapat memperoleh informasi dengan melimpah, cepat, dan mudah dari berbagai sumber dan tempat di dunia. Di sisi lain kita tidak mungkin untuk mempelajari keseluruhan informasi dan pengetahuan yang tersedia karena sangat banyak dan tidak semuanya berguna dan diperlukan (Dikti dalam Hidayat, 2010). Kondisi seperti ini merupakan tantangan yang hanya dihadapi oleh orang-orang terdidik dan mempunyai kemampuan mendapatkan, memilih, dan mengolah informasi atau pengetahuan dengan efektif dan efisien. Agar orang-orang terdidik di masa depan mempunyai kemampuan seperti yang dikemukakan tadi diperlukan sistem pendidikan yang berorientasi pada pemecahan masalah, kemampuan berpikir kritis, kreatif, sistematis dan logis (Depdiknas, 2003). Hal ini sangat mungkin dimunculkan dalam pembelajaran matematika karena mengingat semua kemampuan tersebut merupakan bagian dari tujuan pembelajaran matematika (Depdiknas, 2003). Oleh karena itu pelajaran matematika perlu diberikan kepada setiap siswa sejak sekolah dasar.
secara luwes, akurat, efisien, dan tepat dalam pemecahan masalah. (2) Menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika dalam membuat generalisasi, menyusun bukti, atau menjelaskan gagasan dan pernyataan matematika. (3) Memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh. (4) Mengomunikasikan gagasan dengan simbol, tabel, diagram atau media lain untuk memperjelas keadaan atau masalah. (5) Memiliki sikap menghargai kegunaan matematika dalam kehidupan, yaitu memiliki rasa ingin tahu, perhatian dan minat dalam mempelajari matematika, serta sikap ulet dan percaya diri dalam pemecahan masalah (Depdiknas, 2006).
Tujuan mata pelajaran matematika itu memperlihatkan bahwa salah satu peranan matematika adalah mempersiapkan siswa agar sanggup menghadapi perubahan keadaan atau tantangan-tantangan di dalam kehidupan dan dunia yang selalu berkembang. Persiapan itu dapat dilakukan melalui latihan membuat keputusan dan kesimpulan atas dasar pemikiran secara logis, rasional, kritis, cermat, jujur, efisien dan efektif. Oleh karena itu dalam pembelajaran matematika, siswa harus mulai dibekali dengan keterampilan berpikir kritis. Kemunculan ide, gagasan, proses pencaharian, serta beragamnya pengetahuan awal siswa dalam bidang matematika harus berguna untuk menyelesaikan masalah-masalah di bidang lain.
Anderson (Hendrayana, 2008) bila berpikir kritis dikembangkan, seseorang akan cenderung untuk mencari kebenaran, berpikir divergen (terbuka dan toleran terhadap ide-ide baru), dapat menganalisis masalah dengan baik, berpikir secara sistematis, penuh rasa ingin tahu, dewasa dalam berpikir, dan dapat berpikir kritis secara mandiri. Oleh karena itu diperlukan upaya pendesainan bahan ajar dan kegiatan belajar mengajar untuk memfasilitasi siswa agar kemampuan berpikir kritisnya dapat berkembang.
Kemampuan berpikir kritis dapat dikembangkan melalui pembelajaran matematika di sekolah yang menitikberatkan pada sistem, struktur, konsep, prinsip, serta kaitan yang ketat antara satu unsur dengan unsur lainnya (Maulana, 2008). Matematika dengan hakikatnya sebagai ilmu yang berstruktur dan sistematis, sebagai suatu kegiatan manusia melalui proses yang aktif, dinamis, dan generatif, serta sebagai ilmu yang mengembangkan sikap berpikir kritis, objektif, dan terbuka, menjadi sangat penting dikuasai oleh siswa dalam menghadapi laju perubahan ilmu pengetahuan dan teknologi yang begitu pesat.
Kenyataannya, seperti yang diungkapkan oleh Begle (Ruseffendi, 1991), tidak dapat dipungkiri bahwa anggapan yang saat ini berkembang pada sebagian besar siswa adalah matematika bidang studi yang sulit dan tidak disenangi. Hanya sedikit siswa yang mampu menyelami dan memahami matematika sebagai ilmu yang dapat melatih kemampuan berpikir kritis.
pendidikan semata, tetapi juga sebagai proses fundamental yang memungkinkan siswa untuk mengatasi ketidaktentuan masa mendatang (Cabera dalam Maulana, 2008). Sungguh sangat naif apabila kemampuan berpikir kritis diabaikan oleh guru.
Sebagai upaya mengajarkan atau memfasilitasi siswa agar kemampuan berpikir kritisnya dapat berkembang, maka diperlukan situasi pembelajaran yang dirancang secara tepat. Kemampuan berpikir kritis dapat dikembangkan melalui pembelajaran yang bersifat student-centered (Zohar, 1994).
Upaya memfasilitasi agar kemampuan berpikir kritis siswa berkembang menjadi sangat penting, mengingat beberapa hasil penelitian masih mengindikasikan rendahnya kemampuan berpikir kritis siswa Indonesia. Hasil penelitian Suryanto dan Somerset (Zulkardi, 2001) terhadap 16 Sekolah Lanjutan Tingkat Pertama pada beberapa provinsi di Indonesia menunjukkan hasil tes mata pelajaran matematika sangat rendah, utamanya pada soal cerita matematika (aplikasi matematika). Kemampuan aplikasi merupakan bagian dari domain kognitif yang lebih rendah daripada kemampuan analisis, sintesis, dan evaluasi. Ketiga kemampuan tersebut digolongkan oleh Bloom (Duron, dkk., 2006) dalam kemampuan berpikir kritis.
konsep yang relevan, serta menemukan pola bentuk umum (kemampuan induksi). Hal ini menunjukkan rendahnya kemampuan berpikir kritis siswa, karena menurut Krulik dan Rudnick (Rohayati, 2005) bahwa penalaran mencakup berpikir dasar (basic thinking), berpikir kritis (critical thinking), dan berpikir kreatif (creative thingking).
Rendahnya kemampuan berpikir kritis juga terungkap dari hasil penelitian Mayadiana (2005) bahwa kemampuan berpikir kritis mahasiswa calon guru SD masih rendah, yakni hanya mencapai 36,26% untuk mahasiswa berlatar belakang IPA, 26,62% untuk mahasiswa berlatar belakang Non-IPA, serta 34,06% untuk keseluruhan mahasiswa. Hal serupa juga berdasarkan hasil penelitian Maulana (2008) bahwa nilai rata-rata kemampuan berpikir kritis mahasiswa program D2 PGSD kurang dari 50% skor maksimal.
Dari temuan-temuan di atas dapat dipahami bahwa kemampuan berpikir kritis siswa memang tidak dibiasakan untuk diajarkan sejak sekolah dasar. Sehingga tampak dengan jelas ketika siswa beranjak ke tingkat SMP, SMA hingga perguruan tinggi kemampuan kemampuan berpikir kritis menjadi masalah terhadap mahasiswa itu sendiri. Hal ini akan menjadi sebuah kekhawatiran yang sangat besar jika kemampuan berpikir kritis tidak diajarkan sejak sekolah dasar. Dengan demikian kemampuan berpikir kritis siswa sekolah dasar perlu untuk segera ditingkatkan, karena akan berdampak pada jenjang pendidikan selanjutnya.
Berdasarkan fakta tersebut, maka kemampuan berpikir kritis siswa sangat penting untuk dikembangkan. Oleh karena itu, guru hendaknya mengkaji dan memperbaiki kembali praktek-praktek pengajaran selama ini dilaksanakan, yang mungkin hanya sekadar rutinitas belaka.
Selain mengembangkan kemampuan berpikir kritis, mengembangkan kemampuan komunikasi matematis perlu dilakukan oleh guru dengan cara-cara seperti yang disarankan oleh NCTM dalam standar kurikulumnya. NCTM (1989) menyarankan agar siswa perlu diberi banyak kesempatan untuk menunjukkan kemampuan berkomunikasi dalam pembelajaran matematika dengan jalan mengemukakan ide-ide matematika mereka melalui lisan, tulisan, demonstrasi, dan melalui gambar-gambar. Selain itu, siswa juga perlu diberi kesempatan untuk dapat memahami, menginterpretasi, dan menilai ide-ide matematika yang diungkapkan dalam bentuk tulisan, lisan atau visual (gambar).
melatih siswa untuk dapat mengomunikasikan gagasan, baik komunikasi lisan maupun komunikasi tulisan. Selanjutnya menurut Turmudi, komunikasi adalah bagian esensial dari matematika dan pendidikan matematika. Hal ini merupakan cara untuk sharing gagasan dan mengklasifikasikan pemahaman.
Kemampuan komunikasi matematis perlu menjadi fokus perhatian dalam pembelajaran matematika, sebab melalui komunikasi, siswa dapat mengorganisasi dan mengonsolidasi berpikir matematikanya dan siswa dapat mengeksplorasi ide-ide matematika (NCTM, 2000). Oleh karena itu, siswa perlu dibiasakan dalam pembelajaran untuk memberikan argumen terhadap setiap jawabannya serta memberikan tanggapan atas jawaban yang diberikan oleh orang lain, sehingga apa yang sedang dipelajari menjadi bermakna baginya. Hal ini berarti guru harus berusaha untuk mendorong siswanya agar mampu berkomunikasi.
Menurut NCTM (1991) komunikasi matematis dapat terjadi ketika siswa belajar dalam kelompok, ketika siswa menjelaskan suatu algoritma untuk memecahkan suatu persoalan, ketika siswa menyajikan cara unik untuk memecahkan masalah, ketika siswa mengkonstruk dan menjelaskan suatu representasi grafik terhadap fenomena dunia nyata, dan ketika siswa memberikan suatu konjektur tentang gambar-gambar. Dari penjelasan tersebut, maka kemampuan komunikasi perlu diperhatikan dalam pembelajaran matematika sebab melalui komunikasi siswa dapat mengorganisasi dan mengonsolidasi berpikir matematisnya dan siswa dapat mengeksplorasi ide-ide matematika.
Rendahnya kemampuan komunikasi matematis ditunjukkan dalam studi Rohaeti (2003) bahwa rata-rata kemampuan komunikasi matematis siswa berada dalam kualifikasi kurang. Demikian juga Purniati (2003) menyebutkan bahwa respons siswa terhadap soal-soal komunikasi matematis umumnya kurang. Hal ini dikarenakan soal-soal pemecahan masalah dan komunikasi matematis masih merupakan hal-hal yang baru, sehingga siswa mengalami kesulitan dalam menyelesaikannya.
Sementara itu pada laporan TIMSS 2003, siswa Indonesia berada pada posisi 34 dari 45 negara yang disurvei. Prestasi Indonesia jauh di bawah Negara-negara Asia lainnya. Dari kisaran rata-rata skor yang diperoleh oleh setiap Negara 400-625 dengan skor ideal 1.000, nilai matematika Indonesia berada pada skor 411. Khususnya kemampuan komunikasi matematis siswa Indonesia, laporan TIMSS (Suryadi, 2005) menyebutkan bahwa kemampuan siswa Indonesia dalam komunikasi matematika sangat jauh di bawah Negara-negara lain. Sebagai contoh, untuk permasalahan matematika yang menyangkut kemampuan komunikasi matematis, siswa Indonesia yang berhasil benar hanya 5% dan jauh di bawah Negara seperti Singapura, Korea, dan Taiwan yang mencapai lebih dari 50%.
menjelaskan setiap jawaban yang diberikan dan memberikan alasan untuk setiap jawaban yang diajukan.
Paradigma baru dalam pembelajaran membuka kesempatan untuk menggunakan dan mengembangkan berbagai model pembelajaran yang berorientasi kepada pengembangan kemampuan komunikasi matematis dan keterampilan berpikir kritis siswa. Pembelajaran hendaknya menekankan keterlibatan siswa secara aktif dalam memahami konsep-konsep atau prinsip-prinsip matematika sehingga memungkinkan pembelajaran menjadi lebih bermakna (meaningful), siswa tidak hanya belajar untuk mengetahui sesuatu (learning to know about), tetapi juga belajar melakukan (learning to do), belajar menjadi diri sendiri (learning to be), belajar mengetahui (learning to know), dan belajar hidup dalam kebersamaan (learning to live together) (UNESCO dalam Mulyasa, 2006).
Moffitt (Permana, 2004) mengatakan bahwa PBM adalah suatu model pembelajaran yang melibatkan siswa aktif secara optimal, memungkinkan siswa melakukan investigasi, pemecahan masalah yang mengintegrasikan keterampilan dan konsep dari berbagai konten area. Model pembelajaran ini meliputi penyimpulan informasi sekitar masalah, melakukan sintesis dan merepresentasikan apa yang didapat dari orang lain. Hal senada dikemukakan oleh Dutch (Amir, 2009) bahwa PBM adalah metode instruksional yang menantang siswa agar belajar untuk belajar, bekerja sama dalam kelompok untuk mencari solusi bagi masalah nyata. Masalah ini digunakan untuk mengaitkan rasa keingintahuan serta kemampuan analisis dan inisiatif atas mata pelajaran. Pembelajaran berbasis masalah mempersiapkan siswa untuk berpikir kritis dan analitis atau menghadapi tantangan yang nanti diperlukan dalam karier dan kehidupan sehari-hari.
Hal ini sesuai dengan pendapat Arends (2008) menyatakan bahwa ada tiga hasil belajar (outcome) yang diperoleh pembelajar yang diajar dengan PBM yaitu: (1) inkuiri dan keterampilan melakukan pemecahan masalah; (2) belajar model peran orang dewasa (adult role behaviors), dan (3) keterampilan belajar mandiri (skills for independent learning). PBM juga bertujuan untuk membantu siswa belajar mandiri. Woods (2000) menyebutkan PBM lebih dari sekadar lingkungan yang efektif untuk mempelajari pengetahuan tertentu. Ia dapat membantu siswa membangun kecakapan sepanjang hidupnya dalam memecahkan masalah, kerja sama tim, dan berkomunikasi.
Pembelajaran Berbasis masalah memiliki ciri-ciri seperti (Tan, 2003; Wee & Kek, 2002); pembelajaran dimulai dengan pemberian masalah, masalah memiliki konteks dengan dunia nyata, siswa secara berkelompok aktif merumuskan masalah dan mengidentifikasi kesenjangan pengetahuan mereka, mempelajari dan mencari sendiri materi yang terkait dengan masalah dan melaporkan solusi dari masalah. Sementara pendidik lebih banyak memfasilitasi.
aktif siswa terhadap materi yang mengarah kepada penyelesaian masalah selama pembelajaran berlangsung.
Dari uraian tentang pembelajaran berbasis masalah dapat dipahami bahwa pembelajaran berbasis masalah dapat memupuk kemampuan berpikir kritis dan kemampuan komunikasi matematis siswa, karena model pembelajaran ini mengharuskan siswa untuk membangun sendiri pengetahuan berdasarkan pola pikir siswa. Dengan model pembelajaran ini siswa dibiasakan untuk berpikir kritis dalam menyelesaikan persoalan matematika yang disajikan dan dari apa yang telah diperoleh siswa kemudian dikomunikasikan kepada siswa lainnya. Dengan ide-idenya tersebut siswa akan memiliki kemampuan komunikasi matematis yang tinggi.
Dari beberapa alasan yang dikemukakan di atas, maka penulis berkeinginan untuk mengajukan sebuah penelitian yang berjudul “Penerapan Pembelajaran Berbasis Masalah Untuk Meningkatkan Kemampuan Berpikir Kritis Dan Komunikasi Matematis Siswa Sekolah Dasar”.
B. Rumusan Masalah
Berdasarkan permasalahan yang telah dipaparkan di atas maka rumusan masalah penelitian ini adalah sebagai berikut:
1. Apakah terdapat perbedaan peningkatan kemampuan berpikir kritis antara siswa yang belajar matematika menggunakan model pembelajaran berbasis masalah dengan siswa yang memperoleh pembelajaran secara konvensional? 2. Apakah terdapat perbedaan peningkatan kemampuan berpikir kritis antara
masalah dengan siswa yang memperoleh pembelajaran secara konvensional ditinjau dari level sekolah (tinggi, sedang, rendah)?
3. Apakah terdapat perbedaan peningkatan kemampuan komunikasi matematis antara siswa yang belajar matematika menggunakan model pembelajaran matematika berbasis masalah dengan siswa yang memperoleh pembelajaran konvensional?
4. Apakah terdapat perbedaan peningkatan kemampuan komunikasi matematis antara siswa yang belajar matematika menggunakan model pembelajaran berbasis masalah dengan siswa yang memperoleh pembelajaran secara konvensional ditinjau dari level sekolah (tinggi, sedang, rendah)?
5. Bagaimana sikap siswa terhadap pembelajaran matematika dengan model pembelajaran berbasis masalah?
C. Tujuan Penelitian
Sesuai dengan rumusan masalah, maka tujuan dari penelitian ini adalah sebagai berikut:
1. Mengetahui perbedaan kemampuan berpikir kritis siswa antara yang belajar matematika menggunakan model pembelajaran berbasis masalah dengan siswa yang menggunakan pembelajaran konvensional.
3. Mengetahui perbedaan kemampuan komunikasi matematis antara siswa yang belajar matematika menggunakan model pembelajaran berbasis masalah dengan siswa yang menggunakan pembelajaran konvensional.
4. Mengetahui perbedaan kemampuan komunikasi matematis siswa antara yang belajar matematika dengan pembelajaran berbasis masalah dan pembelajaran konvensional ditinjau dari level sekolah
5. Mengetahui sikap siswa terhadap model pembelajaran berbasis masalah.
D. Manfaat Penelitian
Penelitian ini diharapkan dapat memberikan masukan yang berarti dalam pemilihan kegiatan pembelajaran matematika di kelas dalam upaya meningkatkan kualitas belajar siswa. Adapun manfaat lain dari penelitian ini yaitu:
1. Bagi kepala sekolah, agar menjadi pertimbangan guna memfasilitasi guru dalam menerapkan pembelajaran berbasis masalah untuk meningkatkan kemampuan berpikir kritis dan kemampuan komunikasi matematis siswa. 2. Bagi guru, menjadi acuan tentang penerapan model pembelajaran berbasis
masalah sebagai alternatif untuk meningkatkan kemampuan berpikir kritis dan komunikasi matematis siswa.
3. Bagi siswa, melalui penggunaan pembelajaran berbasis masalah ini diharapkan dapat meningkatkan motivasi belajar, mengembangkan kemampuan berpikir kritis dan mampu mengomunikasikan gagasannya dengan baik dan lancar.
E. Definisi Operasional
Untuk menghindari terjadinya perbedaan penafsiran terhadap istilah-istilah yang terdapat pada rumusan masalah dalam penelitian ini, perlu dikemukakan definisi operasional sebagai berikut:
1. Pembelajaran berbasis masalah adalah model pembelajaran yang dimulai dengan menghadapkan siswa dengan masalah. Masalah yang diberikan berupa masalah nyata atau masalah yang disimulasikan yang kemudian dipecahakan oleh siswa melalui tahap orientasi siswa kepada masalah, mengorganisasikan siswa untuk belajar, membimbing penyelidikan individual maupun kelompok, mengembangkan dan menyajikan hasil karya pemecahan masalah, serta menganalisis dan mengevaluasi proses pemecahan masalah.
2. Pembelajaran konvensional adalah pembelajaran matematika yang berpusat pada guru. Guru menyampaikan materi pembelajaran di depan kelas, guru mendemonstrasikan penyelesaian masalah atau soal, siswa pasif, pertanyaan dari siswa jarang muncul, berorientasi pada satu jawaban yang benar. Aktivitas siswa mendengarkan, mencatat, bertanya, dan mengerjakan soal secara individual atau bekerja sama. Soal-soal yang diberikan kebanyakan serupa dengan contoh yang telah dijelaskan.
berpikir kritis dalam penelitian ini adalah kemampuan mengidentifikasi konsep, menggeneralisasi suatu situasi yang berkaitan dengan suatu konsep, keterampilan dan pemecahan masalah. Kemampuan tersebut diukur dengan tes kemampuan berpikir kritis, di mana tes yang dimaksud berbentuk soal uraian. 4. Kemampuan komunikasi matematis yang ditelaah dalam penelitian ini adalah:
menyatakan benda nyata, gambar, dan diagram ke dalam ide matematika atau sebaliknya, menyatakan peristiwa sehari-hari dalam bahasa atau simbol matematika atau sebaliknya dan kemampuan menjelaskan ide atau situasi dari suatu gambar yang diberikan dengan kata-kata sendiri dalam bentuk tulisan. Kemampuan komunikasi siswa dalam hal ini diukur dengan tes kemampuan komunikasi, di mana tes yang dimaksud berbentuk soal uraian.
5. Peningkatan kemampuan berpikir kritis dan kemampuan komunikasi matematis dalam penelitian ini ditentukan dengan gain yang ternormalkan dari skor postes dan pretes, yaitu dihitung dengan formula
.
F. Hipotesis
Berdasarkan rumusan masalah, maka hipotesis yang diajukan dalam penelitian ini adalah sebagai berikut:
1. Terdapat perbedaan peningkatan kemampuan berpikir kritis siswa antara yang belajar matematika menggunakan pembelajaran berbasis masalah dengan siswa yang pembelajarannya secara konvensional.
2. Terdapat perbedaan peningkatan kemampuan berpikir kritis siswa antara yang belajar matematika menggunakan pembelajaran berbasis masalah dengan siswa yang pembelajarannya secara konvensional ditinjau dari level sekolah (tinggi, sedang, rendah).
3. Terdapat perbedaan peningkatan kemampuan komunikasi matematis siswa antara yang belajar matematika dengan menggunakan pembelajaran berbasis masalah dengan siswa yang pembelajarannya secara konvensional.
4. Terdapat perbedaan peningkatan kemampuan komunikasi matematis siswa antara yang belajar matematika menggunakan pembelajaran berbasis masalah dengan siswa yang pembelajarannya secara konvensional ditinjau dari level sekolah (tinggi, sedang, rendah).
44 BAB III
METODE PENELITIAN
A. Desain Penelitian
Penelitian ini merupakan penelitian eksperimen karena peneliti melakukan perlakuan kepada subjek penelitian untuk selanjutnya ingin diketahui pengaruh perlakuan tersebut. Pada penelitian ini ada dua kelompok subjek penelitian yaitu kelompok eksperimen dan kelompok kontrol. Kelompok eksperimen mendapat perlakuan pembelajaran matematika dengan model pembelajaran berbasis masalah dan kelompok kontrol dengan perlakuan pembelajaran konvensional. Kedua kelompok diberikan pretes dan postes dengan menggunakan instrumen tes yang sama.
Desain eksperimen yang digunakan dalam penelitian ini adalah desain pretest-postest control group design (Ruseffendi, 1994). Adapun rancangan
penelitiannya dapat dilihat dalam bentuk sebagai berikut:
O X1 O
O X2 O
Keterangan:
O : Tes awal sama dengan tes akhir
X1 : Pembelajaran matematika dengan model pembelajaran berbasis masalah
Langkah-langkah yang ditempuh dalam penelitian ini adalah:
1. Secara acak dipilih dua kelompok dari subjek penelitian yang tersedia, yaitu dari masing-masing kualifikasi sekolah 2 kelas, selanjutnya subjek yang terpilih masing-masing sebagai kelompok eksperimen dan kelompok kontrol. 2. Memberikan pelatihan kepada guru tentang model pembelajaran berbasis
masalah, dan membuat kesepakatan bahwa pembelajaran dilaksanakan oleh guru yang bersangkutan, peneliti bertugas sebagai observer dan patner guru serta pembelajaran dilaksanakan sesuai jadwal yang direncanakan. Pelatihan dilaksanakan tanggal 2 sampai dengan 4 Maret 2011.
3. Setiap kelompok diberikan pretest kemudian menentukan nilai rerata dan simpangan baku dari tiap-tiap kelompok untuk mengetahui kesamaan tingkat penguasaan kedua kelompok terhadap kemampuan berpikir kritis dan kemampuan berkomunikasi.
4. Memberikan perlakuan kepada tiap-tiap kelompok, perlakuan yang diberikan kepada kelompok eksperimen yaitu model pembelajaran berbasis masalah sedangkan kepada kelompok kontrol diberikan perlakuan dengan pembelajaran konvensional.
5. Tahap selanjutnya kepada setiap kelompok diberikan postes untuk mengetahui kemampuan berpikir kritis dan kemampuan komunikasi matematis.
7. Menggunakan Uji Anova dua jalur, untuk mengetahui perbedaan peningkatan kemampuan berpikir kritis dan kemampuan komunikasi matematis antara siswa yang menggunakan pembelajaran matematika dengan pembelajaran berbasis masalah dengan yang menggunakan pembelajaran konvensional ditinjau dari level sekolah.
B. Subyek Penelitian
Subyek penelitian ini adalah siswa kelas IV SD di Kecamatan Makmur Kabupaten Bireuen. Dari sebanyak 13 sekolah, terlebih dahulu sekolah digolongkan ke dalam tiga kategori, yaitu sekolah dengan level tinggi, sedang dan rendah berdasarkan data hasil UASBN tahun 2010. Dengan menggunakan stratified random sampling, dari setiap level sekolah akan dipilih secara acak satu
atau dua sekolah, yaitu: SDN 1 Makmur dan SD 7 Makmur yang mewakili sekolah kualifikasi rendah; SDN 5 Makmur sekolah kualifikasi sedang; SDN 10 Makmur dan SD 6 Makmur yang mewakili sekolah kualifikasi tinggi.
C. Waktu dan Materi Pembelajaran
Waktu penelitian direncanakan selama satu bulan, 5 kali pertemuan yang masing-masing pertemuan 2 x 40 menit. Materi tersebut merujuk pada kurikulum 2006. Secara lengkap analisis materi pelajaran dapat dilihat dalam Tabel 3.1 berikut ini.
Tabel 3.1
Analisis Materi Pelajaran
No Materi Alokasi Waktu
1. Menjelaskan Arti Pecahan dan urutannya 2 jam pelajaran 2. Pecahan Senilai dan Menyederhanakan 2 jam pelajaran
3. Menjumlahkan Pecahan 2 jam pelajaran
4. Mengurangkan Pecahan 2 jam pelajaran
5. Menyelesaikan masalah yang berkaitan dengan pecahan 2 jam pelajaran
D. Pengembangan Instrumen Penelitian
1. Instrument Penelitian
Penelitian ini melibatkan dua jenis instrument, yaitu tes dan nontes. Instrumen jenis tes terdiri dari dua sub tes yang berbentuk tes uraian. Tes yang pertama untuk mengukur kemampuan berpikir kritis dan tes ke dua untuk mengukur kemampuan komunikasi matematis siswa. Sedangkan instrument non tes berupa skala sikap, observasi, dan daftar isian guru untuk mengetahui sikap siswa selama proses pembelajaran berlangsung dengan menggunakan pembelajaran berbasis masalah.
uji coba instrumen kemudian dianalisis dengan menggunakan program Anates Versi 4.0.5. Setiap instrumen penelitian ini selanjutnya dibahas sebagai berikut.
a. Tes kemampuan Berpikir Kritis
Tujuan dari penyusunan soal tes berpikir kritis matematis adalah untuk mengukur kemampuan berpikir kritis matematis sebelum dan setelah proses pembelajaran. Soal yang dibuat berupa tes uraian yang soalnya memuat aspek-aspek kemampuan berpikir kritis. Dipilihnya tes berbentuk uraian dimaksudkan agar dapat terlihat kemampuan menganalisis argumen serta kemampuan melakukan dan mempertimbangkan induksi dalam proses menjawabnya serta dimaksudkan juga untuk meminimalisir unsur tebakan.
Kemampuan berpikir kritis dalam hal ini merupakan kemampuan secara menyeluruh terhadap materi yang telah disampaikan setelah kedua kelompok mendapat perlakuan. Tes kemampuan berpikir kritis matematika dalam hal ini terdiri dari 5 soal dalam bentuk uraian. kriteria pemberian skor untuk soal tes kemampuan berpikir kritis matematik dapat dilihat dalam Tabel 3.2 berikut ini.
Tabel 3.2
Kriteria Skor Kemampuan Berpikir Kritis
Respon Siswa Skor
Jawaban lengkap dan benar untuk pertanyaan yang diberikan Ilustrasi dari indikator yang diukur sempurna
Pekerjaannya ditunjukan dan atau dijelaskan (clearly) Membuat sedikit kesalahan
4
Jawaban benar untuk masalah yang diberikan Ilustrasi dari indikator yang diukur baik (good) Pekerjaannya ditunjukan dan atau dijelaskan Memuat beberapa kesalahan
Beberapa jawaban dari pertanyaan tidak lengkap Ilustrasi dari indikator yang diukur cukup (fair) Penyimpulan terlihat tidak akurat
Muncul beberapa keterbatasan dalam pemahaman konsep matematika
Banyak kesalahan dalam penalaran matematika yang muncul
2
Muncul masalah dalam meniru ide matematika tetapi tidak dapat dikembangkan
Ilustrasi dari indikator yang diukur kurang Banyak salah perhitungan yang muncul
Terdapat sedikit pemahaman matematika yang diilustrasikan Siswa jarang mencoba beberapa hal
1
Keseluruhan jawaban tidak tampak Tidak muncul indikator yang diukur
Sama sekali pemahaman matematika tidak muncul Terlihat jelas mencoba-coba atau menebak (bluffing) Tidak menjawab semua kemungkinan yang diberikan
0
Diadaptasi dari Hanchock (Rochaminah, 2008)
b. Tes Kemampuan Komunikasi Matematis
Tes komunikasi matematis ini diberikan sebelum dan sesuadah perlakuan terhadap kelas kontrol dan kelas eksperimen. Pemilihan bentuk tes uraian ini bertujuan untuk mengungkapkan kemampuan komunikasi matematis siswa pada kedua kelompok.
Tes kemampuan komunikasi matematis dalam hal ini terdiri dari 5 soal dalam bentuk uraian. Kriteria pemberian skor untuk tes kemampuan komunikasi matematis berpedoman pada Holistic Scoring Rubrics. Pedoman penskoran ini diadaptasi dari Cai, Lane, dan Jacabcsin (Ansari, 2003) dapat disajikan dalam
Penjelasan secara matematis masuk akal dan benar, serta tersusun secara logis. Membuat gambar lengkap dan benar. Membuat model matematika dan mendapat solusi dengan benar.
4
Penjelasan secara matematis masuk akal dan benar, meskipun tidak tersusun dengan logis. Membuat gambar dengan benar namun kurang lengkap. Membuat model matematika benar namun kurang benar dalam mendapatkan solusi.
3
Penjelasan secara matematis masuk akal namun hanya sebagian lengkap dan benar. Membuat gambar hampir benar, namun tidak lengkap. Membuat model matematika hampir benar namun salah dalam mendapatkan solusi.
2
Hanya sedikit penjelasan gambar atau model matematika benar. 1 Tidak ada jawaban, jika ada maka hanya memperlihatkan bahwa tidak memahami konsep sehingga informasi yang diberikan tidak berarti apa-apa.
0
mendapatkan validitas, reliabilitas, daya pembeda dan tingkat kesukaran maka soal tersebut diujicobakan pada kelas lain di sekolah pada tingkat yang sama.
c. Lembar Observasi
Lembar observasi digunakan untuk mengukur aktivitas siswa dan aktivitas guru selama proses pembelajaran berlangsung. Aktivitas siswa dan guru diamati oleh peneliti sebagai observer. Adapun aspek siswa yang diobservasi terdiri dari delapan aspek yang mengungkapkan aktivitas siswa selama pembelajaran berbasis masalah berlangsung. Data hasil observasi dinyatakan dengan skor 5,4, 3, 2, dan 1 untuk aspek yang diobservasi. Skor tertinggi menunjukkan aktivitas yang sering terjadi dan skor terendah menunjukkan aktivitas yang hampir tidak terjadi.
d. Angket Skala Sikap
Angket skala sikap ini dibuat untuk mengetahui tanggapan siswa terhadap model pembelajaran yang diterapkan. Isi pertanyaan angket berhubungan dengan perasaan dan pendapat selama mengikuti model pembelajaran yang dilaksanakan, serta pengaruh model pembelajaran yang dilaksanakan terhadap kondisi belajar.
e. Daftar Isian Guru
Daftar isian guru digunakan untuk mengungkap respon guru kelas terhadap pembelajaran matematika dengan menggunakan model pembelajaran berbasis masalah. Dalam daftar isian memuat pernyataan-pernyataan menyangkut pemahaman awal, tanggapan tentang kelebihan dan kekurangan model pembelajaran yang digunakan, serta tanggapan-tanggapan atau pendapat dan saran yang diberikan tentang efektif atau tidaknya model pembelajaran tersebut dalam pelaksanaan berdasarkan sudut pandangnya guru.
f. Bahan Ajar
Sesuai dengan tujuan penelitian, bahan ajar yang dikembangkan dalam studi ini dirancang sesuai dengan kurikulum sekolah yang berlaku (KTSP 2006) sehingga siswa dimungkinkan mencapai kompetensi matematis yang relevan dengan materi ajar yang dipelajari. Selain itu bahan ajar didesain agar kemampuan berpikir kritis dan kemampuan komunikasi matematis dapat berkembang dengan baik. Bahan ajar yang dikembangkan di kemas dalam bentuk sajian masalah-masalah yang menuntut siswa untuk berpikir kritis dan komunikasi matematis. Selain itu, bahan ajar disusun agar siswa dapat beraktivitas mengarah pada kompetensi yang diharapkan. Bahan ajar yang digunakan pada penelitian ini terdapat pada Lampiran 3.10
g. Kegiatan Pembelajaran
antara siswa yang memperoleh pembelajaran berbasis masalah dengan siswa yang memperoleh pembelajaran biasa.
Kegiatan PBM pada kelas eksperimen dimulai dengan siswa disuguhkan pada permasalahan rutin dan non rutin. Siswa secara kelompok kecil yang terdiri dari 3-5 orang diminta untuk memecahkan masalah tersebut. Peran guru dalam pembelajaran ini lebih banyak sebagai fasilitator. Guru berkeliling dan memberikan bantuan dengan menggunakan teknik scaffolding dan pengajuan petunjuk (clue). Pada kelas kontrol, siswa mendapatkan pembelajaran secara konvensional, yaitu pembelajaran yang biasa mereka peroleh yang dilakukan oleh guru kelasnya. Berikut ini gambaran umum pedagogi yang dilakukan pada kelas eksperimen dan kelas kontrol.
Tabel 3.4
Model Pedagogi Pembelajaran
Pembelajaran Berbasis Masalah Pembelajaran Konvensional Bahan ajar disajikan dalam bentuk
masalah-masalah kontektual yang menuntut siswa melakukan aktivitas berpikir kritis dan komunikasi matematis
Siswa berperan sebagai peserta yang aktif dalam menyelesaikan permasalahan matematik. Penguasaan konsep dibangun oleh siswa sendiri.
Siswa berperan sebagai penerima informasi yang diberikan guru dan berlatih dalam menyelesaikan soal.
Guru berperan sebagai fasilitator yang membantu siswa dalam menyelesaikan permasalahannya dengan memberikan arahan pada penyelesaian masalah siswa dengan menggunakan teknik
scaffolding
Terjadi interaksi yang multi arah antara siswa dengan siswa atau siswa dengan guru.
Hanya terjadi interaksi satu atau dua arah saja.
2. Analisis Instrumen Penelitian
Untuk keperluan pengumpulan data penelitian dibutuhkan suatu instrument berupa tes yang baik. Tes yang baik biasanya memenuhi kriteria validitas tinggi, reliabilitas tinggi, daya pembeda yang baik, dan tingkat kesukaran yang sedang. Untuk mengetahui karakteristik kualitas tes yang digunakan tersebut diuji coba untuk mendapatkan gambaran validitas, reliabilitas, daya pembeda dan tingkat kesukarannya dengan menggunakan Anates Versi 4.0.5 dengan klasifikasi soal tes kemampuan berpikir kritis dan kemampuan komunikasi matematis.
Kelas yang menjadi tempat ujicoba instrumen yaitu kelas V SDN 3 Sukarasa Bandung, karena materi tersebut belum diajarkan di kelas IV.
Adapun hasil uji coba instrument yang kemudian hasilnya dianalisis dengan menggunakan program Anates versi 4.0.5 dapat dideskripsikan sebagai berikut.
a. Validitas butir soal
Pengujian validitas bertujuan untuk melihat tingkat keandalan atau kesahihan (ketepatan) suatu alat ukur. Menurut Ruseffendi (1994), suatu instrumen dikatakan valid bila instrumen itu untuk maksud dan kelompok tertentu, mengukur apa yang semestinya diukur; derajat ketepatan mengukurnya benar; validitasnya tinggi. Pengujian validitas dilakukan dengan analisis faktor, yaitu mengkorelasikan antara skor butir soal dengan skor total dengan menggunakan rumus Pearson Product Moment.
Dengan bantuan program Anates Versi 4.0.5 dapat diperoleh secara langsung koefesien korelasi setiap butir soal. Setelah diketahui koefisien korelasi (rxy), maka langkah selanjutnya adalah mengkonsultasikannya dengan r product moment tabel pada interval kepercayaan 95% dengan derajat kebebasan n – 2.
Tabel 3.5
Analisis Validitas Tes Kemampuan Berpikir Kritis Dan Kemampuan Komunikasi Matematis
No. Soal rxy rtabel Keterangan
1 0,639 0,325 Valid
2 0,761 0,325 Valid
3 0,767 0,325 Valid
4 0,668 0,325 Valid
5 0,697 0,325 Valid
6 0,712 0,325 Valid
7 0,670 0,325 Valid
8 0,801 0,325 Valid
9 0,661 0,325 Valid
10 0,874 0,325 Valid
Berdasarkan Tabel 3.5 dapat diketahui, bahwa untuk setiap soal nilai rhitung lebih dari nilai rtabel. Dengan demikian, semua butir soal dalam tes kemampuan berpikir kritis dan komunikasi matematis adalah valid.
b. Reliabilitas butir soal
r = 0 Tidak berkorelasi 0,00 <r < 0,20 Rendah sekali
0,20 r < 0,40 Rendah
0,40 r < 0,60 Sedang
0,60 r < 0,80 Tinggi 0,80 r < 1,00 Tinggi sekali
r = 1,00 Sempurna
Berdasarkan hasil uji coba reliabilitas butir soal secara keseluruhan diperoleh koefisien korelasi tes sebesar 0,89 yang berarti bahwa tes kemampuan berpikir kritis dan kemampuan komunikasi matematis mempunyai reliabilitas yang tinggi sekali.
c. Tingkat kesukaran
Analisis ini dilakukan untuk mengetahui tingkat kesukaran setiap butir soal (indeks kesukaran), yang akan digunakan dalam menentukan apakah butir soal itu termasuk dalam kelompok soal mudah, soal sedang atau soal sukar. Indeks kesukaran adalah bilangan yang menunjukkan sukar atau mudahnya suatu soal. Besarnya indeks kesukaran antara 0,00 sampai dengan 1,00. Indeks kesukaran ini menunjukkan tingkat kesukaran soal. Indeks kesukaran untuk setiap butir soal menggunakan Anates Versi 4.0.5. Hasil perhitungan tingkat kesukaran dari setiap item soal, kemudian ditafsirkan menurut Arikunto (2009) berikut ini: 0,00 – 0,30 Sukar
0,31 – 0,70 Sedang
Berdasarkan hasil perhitungan terhadap uji coba, diketahui bahwa indeks kesukaran butir tes kemampuan berpikir kritis dan kemampuan komunikasi matematis seperti disajikan dalam Tabel 3.6 di bawah ini. Hasil perhitungan indeks kesukaran butir tes kemampuan berpikir kritis dan kemampuan komunikasi dapat dilihat pada Lampiran 3.4
Tabel 3.6
Analisis Kesukaran Tes Kemampuan Berpikir Kritis Dan Komunikasi Matematis
No Tingkat Kesukaran (%) Interpretasi Tingkat Kesukaran
1 32,95 Sedang
2 31,82 Sedang
3 18,18 Sukar
4 19,32 Sukar
5 26,14 Sukar
6 38,64 Sedang
7 31,82 Sedang
8 34,09 Sedang
9 21,59 Sukar
10 32,95 Sedang
d. Daya pembeda
Untuk mengetahui sebuah soal baik atau tidak, maka soal tersebut perlu dianalisis daya pembedanya. Perhitungan daya pembeda dimaksudkan untuk mengetahui sejauh mana suatu alat tes dapat membedakan antara siswa yang berada pada kelompok atas (kemampuan tinggi) dan siswa yang berada pada kelompok bawah (kemampuan rendah). Adapun kategori daya pembeda suatu soal, menurut Arikunto (2009) diinterpretasikan sebagai berikut:
0,70 < DP 1,00 Baik Sekali 0,40 < DP 0,70 Baik 0,20 < DP 0,40 Cukup 0,00 < DP 0,20 Jelek
Berdasarkan hasil perhitungan data uji coba, diketahui bahwa daya pembeda tes kemampuan berpikir kritis dan kemampuan komunikasi matematis seperti disajikan dalam Tabel 3.7. Hasil perhitungan daya pembeda butir tes kemampuan berpikir kritis dan kemampuan komunikasi selengkapnya dapat dilihat pada Lampiran 3.4
Tabel 3.7
Analisis Daya Pembeda Tes Kemampuan Berpikir Kritis Dan Kemampuan Komunikasi Matematis
No
Soal Daya Pembeda (%)
Interpretasi Daya Pembeda
1 38,64 Cukup
2 50,00 Baik
3 31,82 Cukup
4 38,64 Cukup
6 72,73 Baik Sekali
7 50,00 Baik
8 54,55 Baik
9 29,55 Cukup
10 65,91 Baik
Dari Tabel 3.8 dapat diketahui bahwa 4 soal mempunyai daya pembeda cukup, 5 soal mempunyai daya pembeda baik, dan 1 soal mempunyai daya pembeda baik sekali. Demikian pula persentase setiap butir soal berada di atas 30% atau berada antara 0,30 dan 0,70. Hal ini Sesuai dengan pernyataan para penulis soal bahwa nilai-nilai daya pembeda dianjurkan berada antara 0,30 – 0,70 (Arikunto, 2009).
Berdasarkan hasil analisis validitas, reliabilitas, daya pembeda, dan tingkat kesukaran, maka tes kemampuan berpikir kritis dan komunikasi matematis yang telah diujicobbakan dapat digunakan sebagai instrumen pada penelitian ini. Hasil analisis uji instrumen yang diperoleh dari program Anates Versi 4.0.5 serta klasifikasi interpretasi reliabilitas, daya pembeda, dan tingkat kesukaran secara lengkap disajikan pada Lampiran 3.4
E. Teknik Pengumpulan Data
F. Teknik Pengolahan Data
Data yang terkumpul dalam penelitian ini berupa data kuantitatif yang diolah dengan teknik perhitungan secara statistik menggunakan program SPSS Versi 17. Data tersebut kemudian menjadi bahan rujukan pengambilan keputusan dari dua buah hipotesis penelitian yang diajukan. Untuk mendeskripsikan hasil penelitian, maka dibutuhkan data pendukung berupa hasil observasi pembelajaran, angket siswa serta daftar isian guru yang dibagikan kepada guru.
Untuk mengetahui peningkatan kemampuan berpikir kritis dan kemampuan komunikasi matematis siswa antara yang belajar matematika menggunakan pembelajaran berbasis masalah dengan siswa yang pembelajarannya secara konvensional, maka data yang diolah berupa skor tes awal dan tes akhir pada kedua kelas. Perbedaan yang terjadi pada kedua kelas dihitung dengan membandingkan rerata skor tes (uji beda), baik tes awal maupun tes akhir, serta peningkatan skornya (N-gain). Untuk mengetahui perbedaan peningkatan kemampuan berpikir kritis dan kemampuan komunikasi matematis siswa antara yang diajarkan dengan pembelajaran berbasis masalah dibandingkan dengan pembelajaran konvensional berdasarkan level sekolah, digunakan uji anova dua jalur (Two Way Anova)
uji beda menggunakan Uji t (Independent Sample T Test), jika data berdistribusi normal dan homogen. Namun jika data tidak berdistribusi normal atau tidak homogen maka digunakan uji statistik non parametrik yaitu uji dua sampel independen (Two Independent Sample Tests/Mann-Whitney U).
Peningkatan yang terjadi sebelum dan sesudah pembelajaran dihitung dengan rumus gain faktor (N-gain). Rumusnya adalah sebagai berikut:
g
(Hake dalam Meltzer, 2002)
keterangan:
SPost = Skor Postes SPre = Skor Pretes SMaks = Skor Maksimum
Hasil perhitungan N-gain kemudian diinterpretasikan dengan menggunakan klasifikasi dari Hake dalam Meltzer yaitu:
Tabel 3.8 Klasifikasi N-gain (g)
Besarnya g Interpretasi
g > 0,7 Tinggi
0,3 g 0,7 Sedang
g < 0,3 Rendah
Sumber: Hake dalam Meltzer (2002)
G. Teknik Analis Data
H0: H1:
Uji hipotesis menggunakan uji tdengan menggunakan uji statistik Compare Mean Independent Sample Test dan Anova dua jalur, setelah sebelumnya dilakukan uji Normalitas dan uji Homogenitas Varians dengan SPSS versi 17.0
H. Prosedur Penelitian
Prosedur penelitian ini dikelompokkan dalam tiga tahap, yaitu: tahap persiapan, tahap pelaksanaan, dan tahap analisis data. Prosedur penelitian ini dirancang untuk memudahkan dalam pelaksanaannya.
1. Tahap Persiapan
dan penyempurnaan instrument tes. Perangkat lain yang disusun adalah skala sikap siswa, lembar observasi aktivitas siswa dan guru, dan daftar isian guru.
Selanjutnya, peneliti mengimformasikan ke sekolah yang menjadi lokasi penelitian untuk mengkonsultasi waktu, teknis pelaksanaan penelitian dan berkonsultasi dengan guru matematika. Kemudian memilih secara acak 3 sekolah dari 6 sekolah yang telah dijadikan sebagai sampel penelitian untuk menentukan kelas eksperimen dan kelas kontrol. Kelas eksperimen mendapat pembelajaran berbasis masalah, sedangkan kelas kontrol memperoleh pembelajaran konvensional.
2. Tahap Pelaksanaan
Memberikan pelatihan-pelatihan tentang bagaimana cara dan proses pembelajaran dengan mengunakan model pembelajaran berbasis masalah kepada guru-guru yang bersangkutan. Langkah selanjutnya melaksanakan tes awal (pretest) pada kelas eksperimen dan kelas kontrol untuk mengetahui kemampuan awal siswa terhadap materi yang akan diberikan sebelum perlakuan dilaksanakan. Setelah tes awal dilaksanakan, diberi perlakuan terhadap kedua kelas, yaitu pembelajaran dengan model pembelajaran berbasis masalah di kelas eksperimen dan pembelajaran konvensional di kelas kontrol. Pembelajaran dilaksanakan selama 5 (lima) kali pertemuan. Saat pembelajaran berlangsung peneliti berperan sebagai observer.
pengisian skala sikap di kelas eksperimen. Sedangkan daftar isian guru diisi oleh guru matematika yang mengajar di kelas eksperimen.
3. Tahap Pengolahan dan Analisis Data
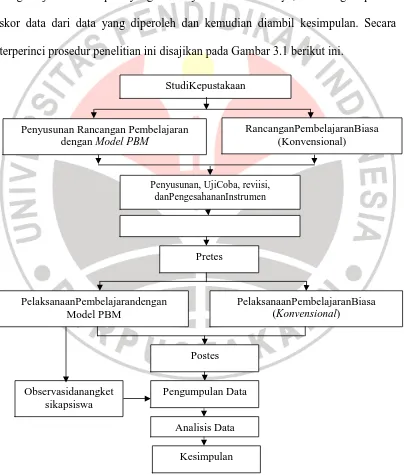
Pada tahap ini peneliti melakukan pengolahan dan analisis skor data tes dengan uji statistik seperti yang telah dijelaskan sebelumnya, dan mengintepretasi skor data dari data yang diperoleh dan kemudian diambil kesimpulan. Secara terperinci prosedur penelitian ini disajikan pada Gambar 3.1 berikut ini.
Gambar 3.1 Prosedur Penelitian PelaksanaanPembelajarandengan
Model PBM
PelaksanaanPembelajaranBiasa (Konvensional)
Postes
Kesimpulan StudiKepustakaan
RancanganPembelajaranBiasa (Konvensional) Penyusunan Rancangan Pembelajaran
dengan Model PBM
Penyusunan, UjiCoba, reviisi, danPengesahananInstrumen
Analisis Data Observasidanangket
sikapsiswa
Pretes
121 BAB V
KESIMPULAN DAN SARAN
A. KESIMPULAN
Berdasarkan hasil penelitian seperti yang telah dikemukakan pada bab sebelum ini, diperoleh kesimpulan sebagai berikut:
1. Terdapat perbedaan peningkatan berpikir kritis antara siswa yang belajar
matematika menggunakan model pembelajaran berbasis masalah dengan siswa
yang memperoleh pembelajaran konvensional. Siswa pada kelas pembelajaran
berbasis masalah mengalami peningkatan kemampuan berpikir kritis yang
lebih tinggi daripada siswa pada kelas konvensional.
2. Terdapat perbedaan peningkatan kemampuan berpikir kritis antara siswa yang mengikuti pembelajaran berbasis masalah dengan siswa yang mengikuti pembelajaran konvensional ditinjau dari level sekolah (tinggi, sedang, dan rendah). Pada pembelajaran berbasis masalah, peningkatan kemampuan berpikir kritis pada siswa sekolah level tinggi lebih tinggi daripada peningkatan kemampuan berpikir kritis pada siswa sekolah level sedang dan kurang.
3. Terdapat perbedaan peningkatan kemampuan komunikasi matematis antara
siswa yang belajar matematika menggunakan model pembelajaran berbasis
masalah dengan siswa yang memperoleh pembelajaran konvensional. Siswa
pada kelas pembelajaran berbasis masalah mengalami peningkatan
kemampuan komunikasi matematis yang lebih tinggi daripada siswa pada
4. Terdapat perbedaan peningkatan kemampuan komunikasi matematis antara siswa yang mengikuti pembelajaran berbasis masalah dengan siswa yang mengikuti pembelajaran konvensional ditinjau dari level sekolah (tinggi, sedang, dan rendah). Pada pembelajaran berbasis masalah, peningkatan kemampuan berpikir kritis pada siswa sekolah level tinggi lebih tinggi daripada peningkatan kemampuan berpikir kritis pada siswa sekolah level sedang dan kurang.
5. Sikap siswa terhadap pembelajaran matematika dengan model pembelajaran berbasis masalah menunjukkan sikap yang positif.
B. SARAN
Berdasarkan kesimpulan dari penelitian ini, dapat dikemukakan saran-saran sebagai berikut.
1. Berdasarkan hasil penelitian, pembelajaran berbasis masalah (PBM) dapat diimplementasikan di sekolah-sekolah level sedang dan level tinggi atau identik dengan sekolah-sekolah yang memiliki kemampuan siswa dengan kemampuan awal paling tidak cukup baik. Namun untuk sekolah-sekolah dengan level kurang, disarankan agar permasalahan yang diberikan benar-benar disesuaikan dengan kemampuan awal siswa dan bimbingan guru kepada siswa dalam kelompok harus semaksimal mungkin.
dan sukar bagi siswa untuk dicari solusinya. Dengan demikian disarankan bagi yang ingin menggunakan PBM agar dapat merancang masalah yang benar-benar sesuai dengan kemampuan awal siswa dan masalah yang diisajikan tidak sukar, sehingga akan mencapai hasil yang lebih baik.
3. Dalam PBM, guru seharusnya dapat mengatur waktu secara efektif agar dapat mencapai sasaran yang diinginkan. Oleh karena itu guru matematika harus melakukan persiapan dengan sebaik-baiknya sebelum melaksanakan pembelajaran. Persiapan tersebut berupa sajian masalah sesuai dengan kemampuan awal siswa, menyediakan benda-benda manipulatif untuk membantu pemahaman siswa, dan membentuk kelompok yang memungkinkan siswa untuk belajar secara efektif dan efisien.
4. Bagi guru yang akan mencobakan menggunakan model pembelajaran ini, antara lain perlu memperhatikan hal-hal berikut: (1) bahan ajar yang digunakan harus dirancang dalam bentuk masalah sehingga dapat menjadi motivasi awal untuk terjadinya proses belajar, (2) pada saat siswa sedang berusaha untuk menyelesaikan masalah yang ada, guru jangan terlalu cepat memberikan bantuan sampai siswa benar-benar membutuhkannya, (3) bantuan yang diberikan guru harus seminimal mungkin dan ketika siswa benar-benar membutuhkannya.
dengan pengajuan petunjuk-petunjuk yang menghubungkan pengetahuan awal siswa dengan masalah yang dihadapi sehingga mereka dapat menemukan penyelesaian.
125
DAFTAR PUSTAKA
Akdon. (2008). Aplikasi Statistika dan Metode Penelitian untuk Administrasi dan
Manajemen. Bandung: Dewa Ruche.
Amir, M.T. (2009). Inovasi Pendidikan Melalui Problem Based Learning;
Bagaimana Pendidik Memberdayakan Pemelajar di Era Pengetahuan. Jakarta:
Prenada Media Group.
Ansari, B.I. (2004). Menumbuhkembangkan Kemampuan Pemahaman dan
Komunikasi Matematik Siswa SMU Melalui Strategi Thin-Talk-Write. Disertasi
pada PPs UPI Bandung: Tidak dipublikasikan.
Arends., R.I. (2008). Learning to Teach. Alih Bahasa Helly Prajitno dan Sri Mulyantini. Yogyakarta: Pustaka Belajar.
Arikunto, S. (2009). Dasar-Dasar Evaluasi Pendidikan. Edisi Rev. Cet. 10. Jakarta: Bumi Aksara.
Cotton, K. (1991). Teaching Thinking Skills, [Online]. Tersedia
ttp://www.nwrel.org/scpd/sirs/6/cu11.htm [28 Januari 2011]
Dahar, R.W. (1996). Teori-Teori Belajar. Jakarta: Erlangga
Depdiknas. (2003). Standar Kompetensi Mata Pelajaran Matematika SD dan MI. Jakarta: Depdiknas.
Depdiknas. (2006). Kerangka Dasar dan Struktur Kurikulum Tingkat Sekolah
Dasar/Madrasah Ibtidaiyah. Jakarta: Media Pustaka.
Duron, R., dkk. (2006). Critical Thinking Framework for Any Discipline.
International Journal of Teaching and Learning in Higher Education Vol. 17:
160-166
Fisher, A. (2007). Critical Thinking: An Introduction. Cambridge: University Press.
Hendrayana, A. (2008). Pengembangan Multimedia Interaktif Untuk Meningkatkan
Kemampuan Berpikir Kritis dan Kreatif Siswa SMP dalam Matematika. Tesis
Pada PPs UPI. Bandung: Tidak Diterbitkan.
Herman, T. (2005). Pembelajaran Berbasis Masalah untuk Meningkatkan
Hidayat, R. (2010). Pembelajaran Kontekstual dengan Strategi dalam Upaya
Pengembangan Kemampuan Pemecahan Masalah, Berpikir Kritis, dan Berpikir Kreatif Matematis Mahasiswa Bidang Bisnis. Ringkasan Desertasi
Pada PPs UPI Bandung:
Howey, K.R., et al. (2001). Contextual Teaching and Learning Preparing Teacher to
Enhance Student Succes in The Work Place and Beyond. Washinton: Eric
Clearinghouse on Teaching and Teacher Education.
Hudiono, B. (2005). Peran Pembelajaran Diskursus Multi Representasi Terhadap
Pengembangan Kemampuan Matematik dan Daya Representasi Pada Siswa SLTP. Disertasi pada PPs UPI Bandung: Tidak dipublikasikan.
Hulu, P. (2009). Meningkatkan Kemampuan Penalaran Matematik Siswa Sekolah
Menengah Pertama Menggunakan Pendekatan Pembelajaran Berbasis Masalah. Bandung: PPs UPI. Tesis tidak diterbitkan.
IMSTEP-JICA (1999). Permasalahan pembelajaran matematika SD, SLTP, dan SMU di Kota Bandung: Bandung: FMIPA UPI.
Ibrahim, M., dan Nur, M. (2000). Pengajaran Berdasarkan Masalah. Surabaya: Universitas Negeri Surabaya.
Ismaimuza, D. (2010). Kemampuan Berpikir Kritis dan Kreatif Matematis Siswa
SMP melalui Pembelajaran Berbasis Masalah dengan Strategi Konflik Kognitif. Disertasi pada PPs UPI. Bandung: Tidak Diterbitkkan.
Jarmita, N. (2009). Penerapan Pembelajaran Kooperatif Tipe STAD dalam
Meningkatkan Pemahaman dan Komunikasi Matematis Siswa pada Pokok Bahasan Bangun Ruang. Tesis pada PPs UPI Bandung: Tidak Diterbitkan.
Jacobsen, D.A. (2009). Methods for Teaching: Promoting Student Learning in K-12
Classrooms. Alih Bahasa Achmad Fawaid & Khoirul Anam. Yogyakarta:
Pustaka Pelajar.
Johnson, E.B. (2002). Contextual Teaching & learning. Alih bahasa Ibnu Setiawan. Bandung: MLC
Kramarski, B. (2002). Effects of Computer Algebra System CAS with Metacognitive
Training on Mathematical Reasoning. Journal of computer Assisted Learning
Maulana. (2008). Pendekatan Metakognitif sebagai Alternatif Pembelajaran