KONSEP DAN APLIKASI VEKTOR PADA GARIS DAN BIDANG Bahan Ajar Untuk Mata Kuliah Analisis Vektor
Oleh:
Fiki Alghadari, M.Pd
PENDIDIKAN MATEMATIKA SEKOLAH TINGGI KEGURUAN DAN ILMU PENDIDIKAN (STKIP) KUSUMA NEGARA JAKARTA
KONSEP DAN APLIKASI VEKTOR PADA GARIS DAN BIDANG Fiki Alghadari
Bahan Ajar Analisis Vektor
Pendidikan Matematika STKIP Kusama Negara Jakarta A. Sejarah Perkembangan Vektor
Ilmuwan bernama Josiah Willard Gibbs, pada abad 18 Gibbs dilahirkan di New Haven, Connecticut, USA pada 11 Februari 1839. Gibbs adalah fisikawan dan matematikawan yang banyak menyumbangkan gagasan teoretis termodinamika kimia. Sedangkan dalam matematika menyumbangkan gagasan analisis vektor. Gibbs bukan satu-satunya ilmuwan yang berjasa dalam pengembangan ilmu ini. Vektor mengalami perjalanan panjang sebelum akhirnya diperkenalkannya konsep keilmuan ini. Perkembangan konsep vektor begitu tertutup, bahkan asal-usulnya pun tidak banyak diketahui. Vektor lahir dalam dua dasawarsa pada abad ke-19 dengan gambaran geometris dari bilangan kompleks. Caspar Wessel (1745-1818), Jean Robert Argand (1768-1822), Carl Friedrich Gauss (1777-1855), dan setidaknya satu atau dua orang lainnya menyatakan bahwa bilangan kompleks berfungsi sebagai titik dalam bidang dua dimensi yaitu sebagai vektor dua dimensi.
B. Contoh Kegunaan Vektor
Analisis Vektor dalam matematika adalah salah satu ilmu yang mempelajari analisis riil dari vektor dalam dua atau lebih dimensi. Dalam kalkulus, salah satu fokus dari vektor adalah permasalahan bidang skalar, dimana terdapat suatu nilai dalam setiap titik dalam ruang. Selain itu, juga fokus pada bidang vektor dimana terdapat suatu vektor dalam setiap titik dalam ruang. Kegunaan kalkulus vektor dalam kehidupan sehari-hari untuk sistem navigasi pesawat terbang. Semua pesawat terbang dilengkapi sistem navigasi agar pesawat tidak tersesat dalam penerbangan.
C. Definisi Vektor
Definisi merupakan pernyataan yang bernilai benar karena disepakati, dan tidak dibuktikan. Vektor memiliki konsep dan definisi konsepnya. Beberapa definisi konsep tentang vektor seperti berikut:
Definisi: vektor adalah sebuah besaran yang memiliki panjang dan arah. Definisi di atas menjelaskan bahwa vektor memiliki panjang dan arah, dan itu adalah konsepnya. Dengan adanya konsep ini, vektor menjadi suatu yang berbeda dengan segmen garis dan sinar. Segmen garis hanya memiliki panjang saja namun tidak ada arah, sedangkan sinar hanya memiliki arah namun panjangnya tidak terbatas. Oleh karena itu, vektor dikatakan sebagai segmen garis berarah.
r
Secara geometrik, definisi vektor di atas menjelaskan bahwa vektor merupakan koleksi dari semua segmen garis berarah. Contohnya digambarkan seperti pada gambar 1. Pada gambar tersebut, ada titik O dan titik R. Titik O disebut dengan origin atau initial point dan titik R disebut dengan terminus atau terminal point. Perubahan posisi dari titik O ke titik R menunjukan arah perpindahan dan direpresentasikan dengan garis OR. Panjangnya adalah sepanjang ruas garis OR. Sedangkan secara analitik, vektor pada bidang dua dimensi merupakan pasangan bilangan real
x,y , dinotasikan dengan vektor r, dan ditulis
x yr , . Untuk vektor pada ruang tiga dimensi merupakan tripel dari bilangan real
x,y,z
. Penyajian vektor dalam bentuk lain adalah vektor basis xiyj dan vektor kolom y x. Melihat dari penyajiannya, vektor ini berkaitan dengan system koordinat. Bilangan real x, y, dan z disebut dengan komponen dari vektor. Digambarkan seperti berikut.
r y x yj xi r
Gambar 2. Vektor pada sumbu koordinat
Lebih lanjut, selain berbeda dengan segmen garis dan sinar, vektor juga berbeda dengan scalar. Berikut ini adalah definisi dari skalar.
Definisi: skalar adalah besaran yang dianggap memiliki panjang tapi tidak berarah.
Melihat dari definisi skalar tersebut, ada suatu kesamaan antara skalar dengan segmen garis. Namun skalar tidak dikatakan sebagai segmen garis karena segmen garis memiliki panjang yang selalu positif. Berbeda dengan scalar, yang mana bisa positif atau negatif. Itu adalah pembeda antara skalar dengan segmen garis. D. Aljabar Vektor
Operasi penjumlahan, pengurangan, dan perkalian familiar dalam bilangan atau skalar aljabar, dengan definisi yang sesuai, operasi-operasi tersebut diekstensi pada aljabar vektor. Berikut beberapa definisi fundamental.
Definisi: dua vektor dikatakan sama ketika keduanya mempunyai panjang dan arah yang sama.
Apabila diterjemahkan dengan cara berbeda, definisi di atas sama halnya seperti berikut: ada dua vektor misalkan vektor a
x y z
dan vektor
p q r
b , kemudian vektor a dan vektor b dikatakan sama (ab) apabila p
x , yq, dan zr. Berikut ilustrasinya secara geometri.
Gambar 3. Vektor a sama dengan vektor b
Gambar di atas menunjukan bahwa panjang dan arah dari vektor a dan vektor b adalah sama sehingga ab. Berikut ini satu definisi lain tentang vektor.
Definisi: suatu vektor mempunyai arah berlawanan dengan vektor a tetapi mempunyai panjang yang sama dinotasikan dengan a.
Ilustrasi geometris dari definisi tersebut di atas dapat dilihat pada gambar yang disajikan di bawah.
Gambar 4. Vektor dengan arah berlawanan
Berbagai definisi tentang konsep vektor telah mengawali sebelum sampai pada proses aritmatika. Disini juga masih ada beberapa definisi lain.
Definisi: jumlah atau resultan vektor a dan vektor b adalah vektor c
dibentuk dengan menempatkan initial point dari vektor a pada terminal point dari vektor b dan kemudian gabungkan initial point dari vektor a ke terminal point vektor b . Penjumlahan ini ditulis denganab , atau cab.
Terkait dengan definisi di atas, berikut ini digambarkan ilustrasi penjumlahan dua bauh vektor secara geometri.
Gambar 5. Dua buah vektor dijumlahkan
Definisi: perbedaan dari vektor a dan vektor b , direpresentasikan dengan b
Jika ab, maka ab didefinisikan sebagai vektor nol dan direpresentasikan dengan symbol 0, seperti dijelaskan dalam definisi berikut.
Definisi: suatu vektor dikatakan sama dengan nol ketika panjangnya adalah nol.
Vektor nol adalah suatu vektor yang semua komponennya adalah nol. Oleh karena itu, vektor nol merupakan vektor yang tidak mempunyai panjang serta tidak menunjukan ke suatu arah.
Definisi: product dari vektor a dengan skalar m adalah vektor ma dengan panjang m kali panjang vektor a, dan dengan arah yang sama dengan vektor a apabila m adalah positif, atau arah berlawanan terhadap vektor a apabila m negatif. Jika m0, ma
adalah vektor nol. E. Hukum Aljabar Vektor
Jika a, b, dan c, adalah vektor dan m dan n adalah skalar, maka berlaku hukum aljabar vektor berikut.
1. abba Hukum komutatif untuk penjumlahan 2. a
bc
ab
c Hukum asosiatif untuk penjumlahan 3. ma am Hukum komutatif untuk perkalian4. m
na mn a Hukum asosiatif untuk perkalian5.
mn
amana Hukum distributif 6. m
ab
mamb Hukum distributifCatatan bahwa dalam hukum ini hanya perkalian vektor dengan satu atau lebih skalar digunakan dan tidak untuk penjumlahan vektor. Hukum ini bisa digunakan untuk persamaan vektor dalam cara yang sama sebagai persamaan aljabar ordinary, seperti jika abc maka dengan transpose acb.
F. Hubungan Vektor Independen dari Origin (Titik Asal)
Hubungan antara dua vektor independen dari titik asal bermanfaat untuk mengetahui suatu vektor lain dengan perbandingan tertentu.
Gambar 6. Vektor-vektor dari titik asal
AO OC
m
CO OB
n mCB nAC n m CB AC
n m na mb c na mb m n c mc mb na nc c b m a c n Contoh soal:
Diketahui titik A
5,2,1
dan titik B
9,10,13
. Titik C membagi ruas garis AB dengan perbandingan 1 , ruas garis berarah :3 AC mewakili vektor u dan ruas garis CB mewakili vektor v. Tentukan koordinat titik C, vektor u, dan vektor v. Pembahasan:
3 1 1 2 5 3 13 10 9 1 n m na mb c
24 16 16
6 4 4
4 1 cJadi posisi titik C
6 4 4
.
6 4 4
5 2 1
1 2 3
c a u
9 10 13
6 4 4
3 6 9
b c v Soal latihan1. Diketahui titik A
2 6 5
dan B
x y z
. Titik P
2 4 5
membagi dengan perbandingan AP:PB2:3. Koordinat titik B adalah ….2. Diketahui titik A
4 3 7
dan B
6 7 13
, dan P membagi AB diluar dengan perbandingan 3:2. Koordinat titik B adalah ….3. Diketahui titik titik A
2 3 5
, B
2 3 7
, dan C
x y 10
. Jika A, B, dan C segaris, maka koordinat C adalah ….G. Aplikasi dari Hubungan Vektor Independen
Aplikasi dari hubungan vektor-vektor independen untuk menghitung pembagian ruas garis dengan memanfaatkan vektor yang berpangkal pada titik asal O
0,0,0
.Contoh:
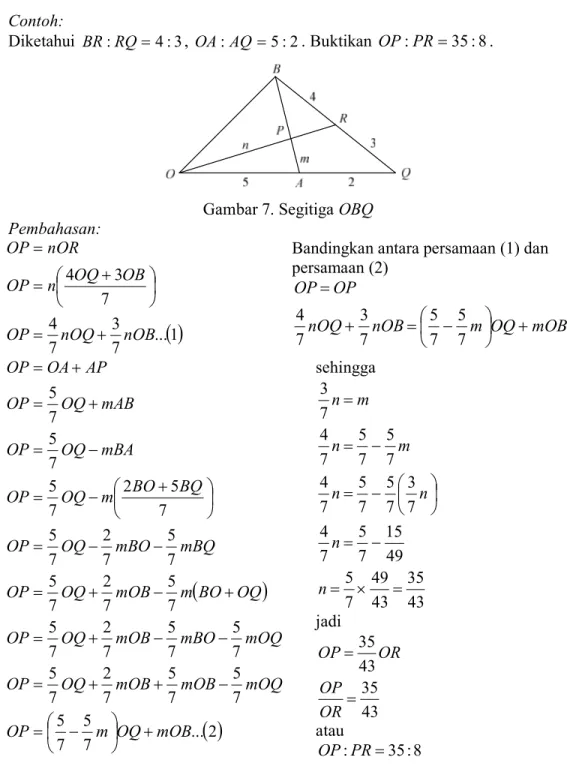
Diketahui BR:RQ4:3, OA:AQ 5:2. Buktikan OP:PR35:8.
Gambar 7. Segitiga OBQ Pembahasan:
1 ... 7 3 7 4 7 3 4 nOB nOQ OP OB OQ n OP nOR OP Bandingkan antara persamaan (1) dan
persamaan (2) mOB OQ m nOB nOQ OP OP 7 5 7 5 7 3 7 4
2 ... 7 5 7 5 7 5 7 5 7 2 7 5 7 5 7 5 7 2 7 5 7 5 7 2 7 5 7 5 7 2 7 5 7 5 2 7 5 7 5 7 5 mOB OQ m OP mOQ mOB mOB OQ OP mOQ mBO mOB OQ OP OQ BO m mOB OQ OP mBQ mBO OQ OP BQ BO m OQ OP mBA OQ OP mAB OQ OP AP OA OP sehingga 43 35 43 49 7 5 49 15 7 5 7 4 7 3 7 5 7 5 7 4 7 5 7 5 7 4 7 3 n n n n m n m n jadi 43 35 43 35 OR OP OR OP atau 8 : 35 :PR OP Soal latihanH. Panjang Vektor
Panjang vektor adalah jarak antara origin dengan terminus. Sebagai contoh, dikatehaui titik O
0,0,0
dan titik A
x,y,z
, maka panjang vektor OA dinotasikan dengan OA
x0
2 y0
2 z0
2.Contoh:
Berapa panjang vektor dari titik P
1,0,2
dan titik A
3,1,2
? Pembahasan
13
2 01
2 22
2 5 PA AP . I. Vektor SatuanSetelah mengetahui panjang vektor, maka setiap vektor dengan panjang tertentu memiliki vektor satuan masing-masing, dan didefinisikan sepert berikut.
Definisi : vektor satuan adalah vektor yang arahnya sama dan panjangnya satu satuan. Vektor satuan dinotasikan dengan e (dibaca e topi),r
x y z
z y x r r er 2 2 2 1 . Contoh:Diketahui vektor u
1 2 3
, hitung panjang vektor dan vektor satuannya. PembahasanPanjang vektor u 122232 14, vektor satuan 1/ 14
1 2 3
u
e .
J. Direct Product (Perkalian Skalar)
Direct product biasa juga dikenal dengan istilah dot product, inner product, scalar product, atau perkalian skalar. Istilah-istilah ini akan digunakan secara bergantian dalam menyebut istilah yang menyatakan kondisi tersebut. Berdasarkan sifat perkalian skalar vektor dalam hukum aljabar, diketahui bahwa jika vektor u dikalikan dengan skalar c, maka panjangnya juga dikalikan dengan
c , jadi cu c u . Berikut definisi mengenai direct product.
Definisi : direct product dari vektor u dan vektor v adalah skalar yang diperoleh dari perkalian dari panjang-panjang vektor dengan nilai cosinus dari sudut diantara kedua vektor.
Perkalian skalar dua vektor misalkan vektor u
u1 u2 u3
dan
v1 v2 v3
v dinamakan dengan hasil kali titik, dan dinotasikan dengan uv, dibaca u dot v. Perkalian scalar vektor u dan v adalah
cos v u v u
dimana θ adalah besar sudut antara vektor u dan vektor v, seperti digambarkan berikut ini.
Gambar 8. Sudut antara vektor u dan v
Karena uv u vcos dan cos
cos
360
cos
, maka perkalian skalar mengikuti hukum komutatif dan distributif. Dalam suatu kasus dua buah vektor yang segaris maka sudut antara dua vektor adalah nol atau 1800 sehingga nilai cosinusnya berturut-turut menjadi positif atau negatif. Oleh karena itu perkalian skalar dari dua vektor sejajar secara numerik sama dengan perkalian dari panjangnya. Tanda menjadi positif ketika arah vektor sama, dan negatif ketika arahnya berlawanan. Akibatnya, perkalian skalar dengan vektor itu sendiri akan menjadi vektor nol.Sedangkan pada kasus lain, misalkan vektor u dan vektor vtegak lurus dengan besar sudut plus atua minus 900 sehingga nilai cosinusnya menjadi 0 dan perkalian skalar menjadi 0 juga. Oleh karena itu, berdasarkan vektor basis,
k u j u i u
u 1 2 3 dan vv1iv2jv3k, untuk vektor satuan i,j,k, maka 1 i j j k k
i dan jkkiij0. Dengan demikian, hasil kali titik menjadi skalar.
3 3 2 2 1 1 3 3 2 3 1 3 3 2 2 2 1 2 3 1 2 1 1 1 3 3 2 3 1 3 3 2 2 2 1 2 3 1 2 1 1 1 3 2 1 3 2 1 1 0 0 0 1 0 0 0 1 v u v u v u v u v u v u v u v u v u v u v u v u v u v u k k v u j k v u i k v u k j v u j j v u i j v u k i v u j i v u i i v u v u k v j v i v k u j u i u v u Soal latihan1. Jika vektor a dan b membentuk sudut 600, a 2 dan a 5, maka tentukan
b a
a .
2. Vektor u
k3 k3 k2
tegak lurus terhadap vektor
1 1 3
, berapanilai k.
3. Diberikan u 4 3, v 5, dan
uv
uv
13. Berapa besar sudut antara vektor u dan v.4. Diketahui u 2, v 3, dan uv 5 . Berapa besar sudut antara vektor u dan v.
5. Diketahui u 29,
uv
uv
1 dan v
vu
30. Berapa besar sudut antara vektor u dan v.6. Diketahui vektor a
2 p 2 2
, b
1 1 2
. Jika
a,b 600,tentukan nilai perbandingan cosinus sudut antara vektor a dan vektor ab. 7. Diketahui dua buah vektor, yaitu vektor a dan b. Jika a 12, b 15 dan
24
b
a , berapa ab .
8. Diketahui segitiga ABC dengan titik A
4,0,8
, B
8,2,6
, dan C
4,0,10
. Hitung nilai cosinus sudut terbesar segitiga ABC.K. Proyeksi Vektor
Proyeksi orthogonal adalah proyeksi yang tegak lurus pada garis atau bidang frontal. Pada vektor, proyeksi ada dua macam yaitu proyeksi skalar orthogonal dan proyeksi vektor orthogonal. Pemanfaatan kedua proyeksi ini misalnya digunakan untuk menghitung jarak suatu titik terhadap suatu garis pada bangun ruang.
1. Proyeksi skalar orthogonal vektor u pada v adalah panjang vektor u yang diproyeksi pada arah vektor v.
Gambar 9. Proyeksi orthogonal vektor u pada v Dari ilustrasi gambar, sehingga diperoleh bahwa
v u v u u u c cos atau v v u c
2. Proyeksi vektor orthogonal vektor u pada v adalah vektornya vektor u yang diproyeksi pada vektor v.
1 2 3
2 v v v v v u v v v v u c . Soal latihan1. Panjang proyeksi vektor a
2 1 p
pada vektor b
p 1 1
adalah 3/
2 . Berapa nilai p.
2. Diketahui vektor a
1 2 2
; b
x 1 1
, dan panjang proyeksi vektor a pada b adalah 6/3. Jika sudut antara vektor b dan a lancip, berapa nilai x. 3. Diketahui vektor a
1 2 2
dan b
2 1 1
, maka proyeksi vektororthogonal vektor a pada arah vektor b adalah ....
4. Diketahui vektor a
2 2 1
, b
3 2 2
dan c
4 3 0
, maka proyeksi vektor orthogonal vektor
2ab
pada arah vektor c adalah .... 5. Diketahui vektor a
3 1 5
dan a
1 2 2
. Proyeksi ortogonalvektor a pada b adalah ....
6. Diketahui panjang proyeksi vektor u
3 3 1
dan v
3 p 3
adalah 3/2. Berapa nilai p.7. Diketahui vektor u
3 4 x
, v
2 3 6
, jika panjang proyeksi vektor u pada v adalah 6, berapa nilai x.8. Diketahui vektoru
1 1 2
,v 2 2 p
,w 0 q 2
. Jika panjang proyeksi vektor v pada vektor u adalah 1, dan vektor v tegak lurus dengan vektor w, berapa nilai pq.9. Diketahui vektor u
2 4 6
dan v
2 2 4
. Tentukan proyeksi skalar dan vektor orthogonal upada v.10.Diketahui vektor a
x1 x
, b
2x 3x1
, dan vektor p adalah proyeksi vektor b ke a. Jika p 2a maka tentukan nilai x yang memenuhi.L. Aplikasi Proyeksi Vektor dalam Dimensi Ruang
Berdasarkan penyajiannya, vektor dinotasikan dalam beberapa bentuk diantaranya vektor basis, vektor kolom, dan vektor baris. Dari penyajian tersebut, terlihat bahwa komponen-komponen vektor termuat dalam dimensi dua (bidang datar x dan y) dan dimensi tiga (bangun ruang x, y, dan z). Pemanfaatan aplikasi vektor dalam ruang berdimensi tiga contohnya untuk menghitung jarak antara titik dan titik, jarak antara titik dan garis.
Menghitung jarak antara titik dan titik dengan memanfaatkan perhitungan panjang vektor. Sedangkan menghitung jarak antara titik dan garis dengan memanfaatkan proyeksi vektor, karena sesuai definisi bahwa jarak antara titik dan garis merupakan jarak terdekatnya. Jarak terdekat antara titik dan garis adalah jarak tegak lurus dari titik ke garis, sehingga konsep proyeksi ortogonal vektor diaplikasikan dalam contoh soal berikut.
Contoh:
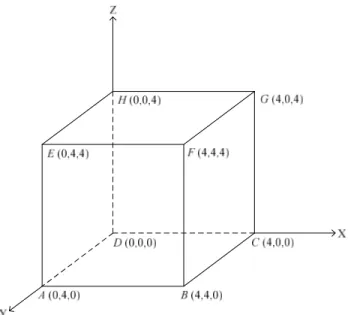
Pada gambar di bawah, diketahui titik P pada pertengahan garis BC. Jika jarak titik F ke garis AP adalah jarak terdekat antara titik dan garis, maka hitung jarak titik F ke garis AP. Gunakan perhitungan dengan memanfaatkan proyeksi ortogonal vector.
Gambar 10. Kubus pada Ruang Koordinat Pembahasan
Dengan hubungan vektor-vektor independen, maka diketahui koordinat P
4,2,0
. Vektor APv
4 2 0
, v 4222 2 5, serta vektor
4 0 4
u AF , u 4242 4 2, sehingga
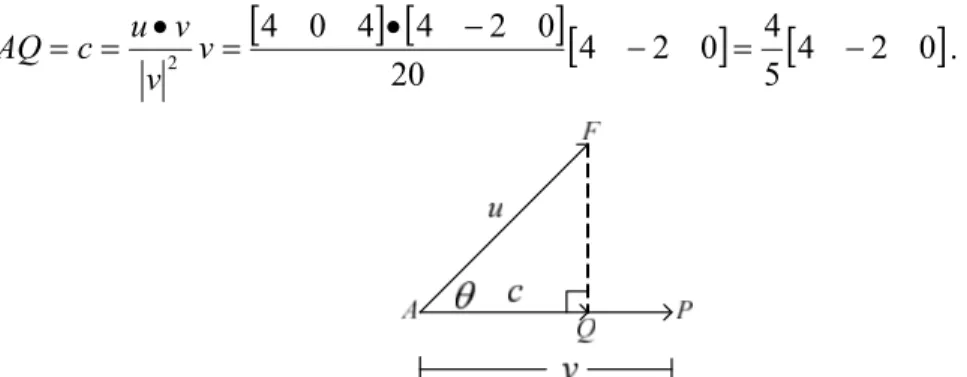
5 5 8 5 2 16 5 2 0 2 4 4 0 4 v v u c AQ .
4 2 0
5 4 0 2 4 20 0 2 4 4 0 4 2 v v v u c AQ .Gambar 11. Ilustrasi Gambar Hubungan Titik F dan Garis AP Jarak titik F ke garis AP dihitung dengan
1 2 20
5 4 4 0 4 0 2 4 5 4 QA AF QF
30 5 4 25 480 4 5 8 5 4 2 2 2 QFatau dengan teorema phytagoras
30 5 4 5 96 5 5 8 2 4 2 2 2 2 c AF AQ FQDengan demikian, jarak titik F ke garis AP adalah 30 5 4
satuan.
Soal Latihan
1. Diketahui titik P di tengah garis GH, titik Q di tengah garis AD. Jika jarak titik F ke garis PQ adalah jarak terdekat antara titik dan garis, maka hitung jarak titik F ke garis PQ.
2. Diketahui titik O di tengah bidang ABCD. Hitung jarak dari titik G ke garis EO.
M.Konsep Persamaan Vektor
Persamaan garis ymxc pada koordinat cartesius menjadi analogi dan pengetahuan awal untuk pengembangan konsep persamaan vektor. Perhatikan gambar berikut.
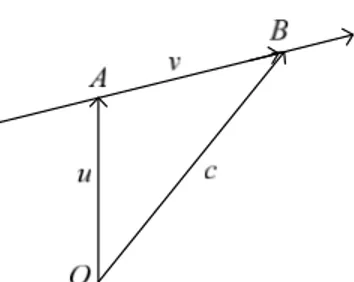
Gambar 12. Vektor u, v, dan c
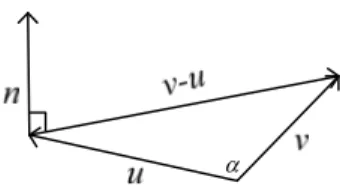
Konsep penjumlahan atau pengurangan dua buah vektor independen dari origin digunakan untuk menyatakan suatu persamaan vektor. Pada gambar 12 di atas, diketahui bahwa vektor c merupakan jumlah antara vektor u dan vektor v, atau cuv. Melihat dari gambar tersebut, vektor c sebagai jumlah dari dua vektor lainnya sangat dipengaruhi oleh kedua vektor itu. Ilustrasinya seperti gambar berikut.
Gambar 13. Ilustrasi hubungan vektor u, v, dan cn
Dari gambar 13 di atas, berdasarkan penjumlahan geometri vektor cuv, dengan merupakan suatu skalar tertentu, sehingga persamaan umum untuk suatu vektor dapat digeneralisasi seperti berikut.
v u c OE v u c OD v u c OC v u c OB n n ... 3 3 2 2 1 1
Artinya, apabila dimisalkan vektor u merupakan suatu vektor dengan posisi yang tetap dan vektor v merupakan vektor dengan panjang yang berubah-ubah dikarenakan oleh suatu skalar tertentu (misalkan dengan ) seperti pada gambar 13, sehingga dengan berubahnya panjang vektor v, maka panjang vektor c juga akan ikut berubah. Dengan demikian perubahan kedua vektor tersebut dibuatkan dalam bentuk persamaan vektor yang diperumum menjadi cn u
nv. Dalam halini, skalar mempengaruhi panjang vektor v akibatnya juga mempengaruhi panjang vektor c. Persamaan vektor ini dapat dimanfaatkan untuk menentukan posisi titik seperti titik B, C, D, ataupun E. Oleh karena itu, persamaan vektor dianalogikan seperti persamaan garis lurus dimana
nv seperti halnya gradient dari garis lurus.N. Persamaan Vektor suatu Garis Lurus
Secara umum, persamaan vektor cn u
nv bisa disajikan dalam tiga bentuk dengan masing-masing bentuk yang saling berkaitan. Berikut ini adalah tiga buah bentuk persamaan vektor tersebut.1. Vector Form
Vector form dari suatu persamaan tidaklah unik sehingga ada banyak perbedaan cara untuk mengekspresikan persamaan.
Gambar 14. Ilustrasi hubungan vektor u, v, dan c.
Ada dua ulasan terkait dengan banyaknya perbedaan cara untuk mengekspresikan persamaan, yaitu arah (direction) dan lokasi. Direction pada gambar 14 direpresentasikan oleh vektor v. Sebagai contoh, misalkan direction vektor seperti
1 2 3
. Itu artinya bahwa untuk setiap perubahan sepanjang 1 unit dalam arah i, garis mengalami perubahan 2 unit dalam arah j, dan 3 unit dalam arah k. Sedangkan lokasi adalah tentang posisi titik, seperti pada gambar 13 yaitu posisi titik B, titik C, atau yang lain. Oleh karena itu, dengan sebagai skalar sehingga membuat posisi titik-titik dilewati oleh garis dan bersesuaian dengan persamaan vektor.Contoh:
Misalkan untuk gambar 14 diketahui bahwa titik O
0,0,0
, A
1,1,1
, dan
1,2,1
B , tentukan vektor form suatu garis yang melalui titik A dan titik B. Pembahasan
Dari ketiga titik, titik O, titik A, dan titik B, diperoleh vektor OAu
1 1 1
dan vektor ABv
2 3 2
, dan sesuai dengan persamaan vektorv u
c , maka vektor form dari gambar 14 di atas adalah
1 1 1
2 3 2
2. Parametric Form
Parametric Form merupakan persamaan vektor dengan memisah-misahkan setiap komponen x, y, dan z. Berikut contoh mengubah vektor form menjadi parametric form. Misalkan diberikan persamaan vektor dengan vector form seperti berikut.
x y z
1 1 2
2 3 2
Mengubah vector form sehingga menjadi parametric form adalah dengan cara memisahkan setiap komponen x, y, dan z, maka diperoleh
2 2 3 1 2 1 z y xJadi persamaan parametric untuk
x y z
1 1 2
2 3 2
adalah x12, y13, dan z22.3. Cartesian Form
Cartesian form merupakan persamaan vektor dengan mengubah bentuk parametric form dengan memisahkan λ ke dalam suatu bentuk yang memuat komponen x, y, atau z seperti berikut.
2 1 2 1 x x 3 1 3 1 y y 2 2 2 2 z z
Jadi cartesian form c
1 1 2
2 3 2
adalah2 2 3 1 2 1 y z x . Soal latihan 1. Ubahlah persamaan vektor berikut ke bentuk lain.
a. r
i j2k
2i3j2k
b. 1 5 5 3 4 z y x c. ; 2 4 7 3 7 5 z y x2. Apakah garis rk
i j3k
dan r
2i j
3j5k
berpotongan atau bersilangan? Jika berpotongan, tentukan titik potongnya. Tentukan juga besar sudut lancip diantara kedua garis itu.3. Apakah garisr
3j2k
2i jk
danr
i2j5k
i j2k
berpotongan atau bersilangan? Jika berpotongan, tentukan titik potongnya. Tentukan juga besar sudut lancip diantara kedua garis itu.4. Persamaan vektor suatu garis diberikan dengan Cartesian form 2 1 3 3 2 6 5 3x y z
. Tentukan persamaan vektor dari garis sejajar yang melalui titik dengan koordinat
3,7,1
dan tentukan posisi titik koordinat garis tersebut dimana z0.5. Tunjukan bahwa garis dengan persamaan r
i2j3k
i j4k
dan r
3i4j11k
5i5j20k
adalah berimpit.6. Tunjulah bahwa garis
3 1 2 4 1 2 3 y z x dan 6 5 4 4 3 4 1 2 y z x adalah sejajar.
7. Tunjukan bahwa garis dengan persamaan vektor r
2i3j
i3j
dan
i i j
r 4 2 6 adalah sejajar, dan tentukan persamaan vektor untuk garis sejajar yang melalui
1 . ,18. Garis l dan m mempunyai persamaan masing-masing
i j k
l i j k
r 3 2 2 dan r
4i4j2k
m
aibjk
, dimana a dan b adalah konstanta.a. Jika garis l dan garis m berpotongan, tunjukan bahwa 2ab4 b. Dan Jika garis l dan garis m saling tegak lurus, tentukan nilai a dan b. c. Dengan nilai konstanta a dan b pada bagian b), tentukan titik potong garis l
dan garis m.
9. Tentukan jarak titik Q dengan koordinat
1,2,3
dari garis lurus dengan persamaan r
3i4j2k
i2j2k
.O. Cross Product (Perkalian Vektor)
Cross product dikenal juga dengan istilah skew products, vektor product, outer product, atau perkalian silang. Istilah-istilah ini akan digunakan secara bergantian dalam menyebut istilah yang menyatakan kondisi tersebut. Berikut ini definisi tentang cross product.
Definisi : cross product (c) dari vektor u dan vektor v dinotasikan dengan v
u
c dan dibaca u cross v . Panjang vektor uv didefinisikan sebagai product dari panjang vektor u dan vektor v dengan sinus sudut antara kedua vektor itu (), atau
sin v u v u
c . Sedangkan arah vektor cuv tegak lurus dengan bidang dari vektor u dan vektor v .
Berdasarkan definisi c uv u v sin, dan sifat-sifat sudut berelasi dalam trigonometri sin
sin
360
sin
, maka berikut ini disajikan sifat-sifat cross product.1. uvvu (anti komutatif) 2. u
vw
uv
uw
(distributif) 3. u
v
u v
uw
4. uu0 dan vv0
Oleh karena itu, vektor basis dalam koordinat kartesian
i,j,k
menurut sifat-sifat skew product berlakuj k i i j k k i j j i k i k j k j i k k j j i i , , , , 0
Dengan demikian, mengingat sifat sifat skew product di atas, maka dengan hukum distributif vektor basis dapat dihitung seperti berikut.
uv uv
i uv uv
j uv uv
k k v j v i v k u j u i u v u 1 2 2 1 1 3 3 1 2 3 3 2 3 2 1 3 2 1 Perkalian vektor basis di atas dapat dinyatakan dalam bentuk determinan matriks berikut.
u v uv
i uv uv
j uv u v
k k v v u u j v v u u i v v u u v v v u u u k j i v u 1 2 2 1 1 3 3 1 2 3 3 2 2 1 2 1 3 1 3 1 3 2 3 2 3 2 1 3 2 1 Contoh:
Ada vektor a
1 2 2
dan b
2 1 1
, tentukan ab. Pembahasan
k j i k j i k j i k j i b a 3 5 4 2 2 1 1 2 2 1 1 2 2 1 2 1 2 2 1 1 2 2 1 1 1 2 2 1 1 2 2 2 1 atau
k j i i j i k j k i j i k j k k k j k i k k j j j i j k i j i i i k j i k j i b a 3 5 4 2 4 2 4 0 2 2 4 2 0 2 4 1 1 0 2 1 2 1 2 2 2 1 2 1 2 2 2 1 1 1 1 2 1 2 2 2 Soal Latihan1. Berikan semua vektor yang tegak lurus terhadap vektor 2i j4k dan k
j i 4 5 3 .
2. Berikan semua vektor yang tegak lurus terhadap vektor i4j3k dan k
j i
4 .
3. Tentukan vektor satuan yang tegak lurus dengan vektor-vektor yang dibentuk oleh titik
1,2,0
,
5,1,3
, dan
4,0,2
.4. Tentukan vektor satuan yang tegak lurus dengan vektor-vektor yang dibentuk oleh titik
0,1,5
,
2,2,2
, dan
3,4,1
.P. Aplikasi Cross Product dan Persamaan Bidang
Berdasarkan definisi dari cross product, maka hasil perkalian silang diaplikasikan untuk mencari persamaan bidang dalam ruang tiga dimensi yang melalui tiga titik tidak segaris. Dari tiga titik yang tidak segaris tersebut akan diperoleh dua buah vektor misalkan vektor u dan vektor v, kemudian dari kedua vektor tersebut dihitung hasil kali silang dan menghasilkan sebuah vektor baru misalkan vektor n. Artinya hasil kali silang yang diperoleh dari uvmerupakan vektor n yang dan vektor n saling tegak lurus dengan vektor u dan vektor v. Vektor n tersebut dinamakan dengan normal bidang.
Gambar 15. Vektor normal bidang .
Persamaan bidang bisa disajikan dalam dua bentuk, yaitu persamaan normal dan persamaan kartesian.
1. Normal equation (persamaan normal)
Sebuah bidang melalui titik p dan tegak lurus dengan normal bidang n dan mempunyai posisi titik r, misal
x,y,z
, sehingga normal equationrn pn. Contoh:Cari persamaan bidang yang melalui titikp1
1,2,3
,p2
4,1,2
, danp3
2,3,0
. PembahasanCara I: Dari tiga titik, diketahui bahwa
3 3 5
2 1 p p u
6 4 2
3 2 p p v
3 3 5
6 4 2
14 24 6
v i j k i j k u sehingga diperoleh
1, 2,3
14 24 6
44 1n p .Jadi normal equationnya adalah r
14 24 6
44Cara II: Karena normal bidang n
x y z
adalah vektor yang tegak lurus dengan setiap vektor yang berada pada bidang, vektor u dan vektor v, maka0 n
u dan vn0, sehingga diperoleh dua persamaan:
0 2 4 6 0 5 3 3 z y x z y x
Dengan mengeliminasi variable x dari dua persamaan di atas, maka diperoleh 0 8 2y z , sehingga . 2 8 8 2 0 8 2 z y z y z y
Jadi, untuk y8 dan z2 maka ketika disubsitusi ke persamaan 0
5 3
3
x y z akan diperoleh x14/3, sehingga normal bidang
14/3 8 2
n dan p1n
1,2,3
14/3 8 2
44/3. Dengan demikian normal equationnya adalah r
14/3 8 2
44/3.2. Cartesian equation (persamaan kartesian)
Apabila r
x,y,z
dan n
p,q,r
, sehingga persamaan rn pn menjadi np rz qy
px . Persamaan pxqyrz pn dinamakan dengan persamaan cartesian (cartesian equation) dari persamaan bidang.
Persamaan normal untuk persamaan bidang yang melalui titikp1
1,2,3
,
4,1,2
2
p , danp3
2,3,0
adalah r
14 24 6
44. Apabila persamaan normal tersebut dibuat ke bentuk persamaan kartesian menjadi44 6 24
14x y z . Sedangkan untuk persamaan normal
14/3 8 2
44/3
r apabila dibuat ke bentuk persamaan kartesian akan menjadi 14x/38y2z44/3. Bandingkan antara persamaan kartesian dengan , apakah kedua persamaan tersebut sama?
Soal Latihan
1. Cari persamaan bidang yang melalui
2,5,6
,
1,1,2
, dan
4,0,6
. 2. Cari persamaan bidang yang melalui
1,2,3
,
4,2,1
, dan
5,1,6
.3. Cari persamaan bidang yang melalui
1,2,3
dan tegak lurus terhadap dua bidang 2x2yz3 dan x3y2z7.4. Cari persamaan bidang yang melalui
2,3,2
dan sejajar bidang dengan vektor 4i3jk dan 2i5j6k.5. Cari persamaan bidang yang melalui
6,2,1
dan tegak lurus pada garis potong bidang 4x3y2z50dan 3x2yz110.6. Find the cartesian equation of the plane which passes through the point
3,4,1
and which is parallel to the plane containing the point
1,2,1
and the line r
1 1 1
.7. Persamaan bidang yang memuat garis x12t, y13t, z4t, dan titik
1,1,5
adalah ….Q. Hubungan Persamaan Vektor suatu Garis dan Persamaan Bidang
Berbicara mengenai vektor dan bidang, kedua komponen ini berada dalam system koordinat ruang tiga dimensi. Ada dua kemungkinan hubungan antara vektor dan bidang, yaitu vektor berada pada bidang, atau vektor berimpit dengan bidang.
Gambar 16. Hubungan Vektor dan Bidang
Namun apabila vektor tidak terletak pada bidang, walaupun vektor dan bidang itu sejajar, maka kondisi ini jelas berada pada ruang tiga dimensi. Berikut kemungkinan hubungan antara vektor dan bidang.
1. Vektor Berimpit dengan Bidang
Direction atau arah vektor dapat ditentukan dari dua buah titik yang disajikan. Dengan kata lain, dari dua buah titik akan membentuk satu vektor dengan suatu panjang dan arah tertentu. Lebih lanjut, untuk memeriksa apakah suatu vektor berimpit dengan bidang yaitu dengan cara mensubsitusikan titik yang diketahui dan dilewati vektor tersebut. Apabila hasil subsitusi titik–titik itu memenuhi persamaan bidang maka tentu titik-titik itu dimuat oleh bidang. Artinya titik berada pada bidang dan vektor yang melalui titik tersebut berimpit dengan bidang. 2. Vektor Sejajar Bidang
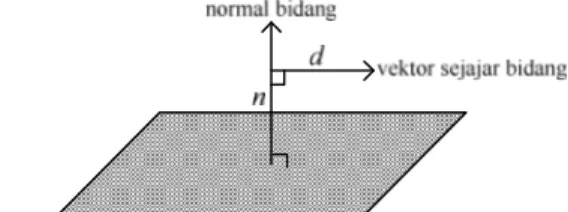
Suatu vektor dikatakan sejajar bidang apabila nilai dot product antara normal bidang n dan arah vektor d sama dengan 0. Mengapa demikian? Karena arah vektor (d) sejajar dengan bidang, sementara bidang memiliki vektor normal (n) yang tegak lurus dengan bidang, akibatnya arah vektor (d) akan tegak lurus dengan vektor normal bidang (n) sehingga membentuk sudut 900 dan
0 90 cos cos n d n d n
d
. Ilustrasi bisa dilihat pada gambar.Gambar 17. Ilustrasi vektor yang sejajar dengan suatu bidang
Informasi di atas dapat digunakan untuk memeriksa ketegaklurusan antara suatu vektor dengan suatu bidang.
3. Vektor Tegak Lurus Bidang
Suatu vektor yang diketahui arahnya, atau direction vektor (d), dikatakan tegak lurus bidang dengan vektor normal n, apabila nilai perbandingan antara
direct product (dn) dengan perkalian panjang vektor (d n) sama dengan 1 atau -1. Dengan kata lain, nilai kosinus antara normal bidang n dan direction vektor d sama dengan 1 atau –1, atau
1 cos n d n d atau cos 1 n d n d .
Nilai perbandingan cosinus tersebut akan menjadi 1 apabila besar sudut antara direction vektor d dan vektor normal n sama dengan 0. Namun demikian, perbandingan cosinus akan bernilai 1 apabila besar sudut antara direction vektor d dan vektor normal n sama dengan 1800. Artinya, vektor normal n berlawanan arah dengan direction vektor d, atau nd dengan adalah skalar tertentu yang bernilai negatif. Berikut ilustrasi gambar antara direction vektor d dan vektor normal n.
Gambar 18. Vektor d dan vektor normal n 4. Vektor dan Bidang Membentuk Sudut θ
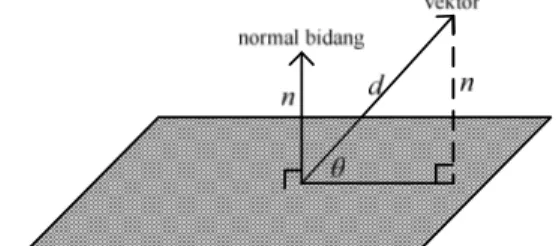
Apabila besar sudut yang dibentuk oleh suatu vektor dan suatu bidang adalah θ, maka besar θ dapat dihitung dengan menggunakan nilai perbandingan trigonometri sinus antara vektor normal bidang n dan direction vektor d, yaitu dengan: n d n d sin
Untuk lebih memahami alasan menggunakan perbandingan nilai sinus dalam perhitungan sudut antara vektor normal bidang n dengan direction vektor d, dapat dianalisis dari gambar berikut.
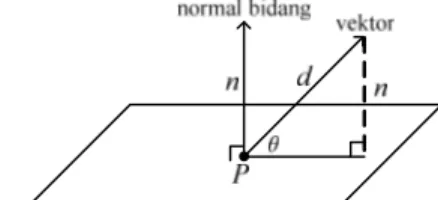
R. Titik Tembus suatu Garis pada Bidang dengan Persamaan Vektor
Titik tembus vektor pada bidang merupakan titik yang dimuat oleh bidang sekaligus dilewati oleh vektor. Berikut ini adalah ilustrasinya geometrinya.
Gambar 20. Vektor d menembus bidang di titik P Contoh:
Tentukan posisi titik tembus persamaan vektor pada bidang apabila diketahui bidang dengan persamaan 2x3y6z8 dan vektor dengan persamaan
3 5 6
2 3 6
r .
Pembahasan
Berdasarkan informasi di atas, diketahui bahwa suatu vektor dengan persamaan
3 5 6
2 3 6
r , dan bidang dengan persamaan 2x3y6z8. Dari persamaan vektor tersebut, diperoleh bahwa
2 3
x , y53, dan z66.
Karena posisi titik x 32, y53, dan z66 juga dimuat bidang, maka posisi titik tersebut disubsitusikan pada persamaan bidang sehingga diketahui nilai yang menjadi scalar pada persamaan vektor.
1 8 6 6 6 3 5 3 2 3 2 8 6 3 2 z y xKemudian 1 disubsitusikan pada persamaan vektor
1 2 0
6 3 2 1 6 5 3 6 3 2 6 5 3 z y x z y x z y x Dengan demikian diperoleh vektor
1 2 0
. Karena vektor tersebut merupakan vektor independent dari origin O
0,0,0
, maka titik koordinat yang merupakan titik tembus persamaan vektor r
3 5 6
2 3 6
pada bidang8 6 3
Soal latihan
1. Diketahui suatu kubus dengan panjang sisi 4 satuan.
Gambar 21. Kubus dalam Koordinat Ruang Tentukan:
a. Persamaan vektor dari garis CE b. Persamaan bidang BDHF
c. Sudut antara garis CE dan bidang BDHF
S. Hubungan suatu Bidang dan Bidang Lain dengan Konsep Vektor
Antara suatu bidang dengan bidang yang lain, satu sama lain memiliki hubungangeometri, seperti: bidang sejajar bidang yang lain, bidang tegak lurus dengan bidang lain, serta bidang membentuk sudut θ dengan suatu bidang lain. 1. Bidang Sejajar Bidang Lain
Suatu bidang dikatakan sejajar dengan bidang lain apabila nilai perbandingan cosinus antara vektor normal bidang n1 dan vektor normal bidang n2 sama
dengan 1 atau –1. atau
1 cos 2 1 2 1 n n n n atau cos 1 2 1 2 1 n n n n
Nilai perbandingan cosinus sama dengan 1 apabila besar sudut antara vektor normal bidang n1 dan vektor normal bidang n2 sama dengan 0. Namun demikian, perbandingan cosinus akan bernilai 1 apabila besar sudut antara vektor normal bidang n1 dan vektor normal bidang n2sama dengan 1800. Artinya, vektor normal
bidang n1 berlawanan arah dengan vektor normal bidang n2, atau n1n2
dengan adalah skalar tertentu yang bernilai negatif. Berikut ilustrasi gambar antara vektor normal bidang n1 dan vektor normal bidang n2.
Gambar 22. Dua Buah Bidang Sejajar dengan Vektor Normal 2. Bidang Tegak Lurus Bidang Lain
Suatu bidang dikatakan tegak lurus bidang lain apabila nilai dot product dari vektor normal bidang n1 berlawanan arah dengan vektor normal bidang n2 sama dengan 0. Ilustrasinya bisa dilihat pada gambar 23.
n1
n2
Nilai dot product sama dengan 0 karena vektor normal bidang n1tegak lurus dengan vektor normal bidang n2. Oleh karena itu, kedua vektor normal bidang membentuk sudut 900, dan n1n2 n1 n2 cos n1 n2 cos900.
3. Bidang Membentuk Sudut θ dengan Bidang Lain
Suatu bidang yang berpotongan dengan bidang lain dan besar sudut yang dibentuk oleh kedua bidang tersebut adalah θ di ilustrasikan seperti di bawah ini.
Gambar 24. Dua Buah Bidang Membentuk Sudut θ
Berdasarkan ilustrasi di atas, maka menentukan besar θ dapat dihitung dengan menggunakan nilai perbandingan cosinus antara vektor normal bidang n1dan
vektor normal bidang n2, yaitu
2 1 2 1 180 cos n n n n atau 2 1 2 1 cos n n n n .Dari algoritma di atas terlihat adacos
180
, ini dikarenakan jumlah antara besarnya sudut yang dibentuk suatu bidang dengan suatu bidang lainnya (θ) dengan besarnya sudut yang dibentuk vektor normal bidang n1 suatu bidang dan vektor normal bidang n2suatu bidang lain sama dengan 1800.Contoh:
Limas T.ABCD beraturan dengan panjang rusuk alas 4 cm dan tinggi 4 cm. Berapa besar sudut antara bidang TAD dan ABCD.
Pembahasan
Misal titik A pada bidang koordinat berada di posisi
0,0,0
, titik B
4,0,0
,
4,4,0
C , maka D
0,4,0
, sehingga T
2,2,4
.Normal bidang TAD ditentukan dengan vektor AT
2 2 4
dan vektor
2 2 4
DT , sehingga diperoleh
2 2 4
2 2 4
16 0 8
1 ATDT n .Normal bidang ABCD ditentukan dengan vektor AB
4 0 0
dan vektor
4 4 0
BD , sehingga diperoleh
4 0 0
4 4 0
4 0 16
2 ABBD n .Nilai perbandingan cosinus sudut antara bidang TAD dan bidang ABCD adalah sebagai berikut
320 272 0.651 128 64 16 4 8 16 16 0 4 8 0 16 cos 2 2 2 2 Dengan demikian, besar sudut antara bidang TAD dan bidang ABCD adalah
0.651
49.399cos1 .
Soal latihan
1. Diketahui suatu kubus dengan panjang sisi 4 satuan. P ditengah GH, Q ditengah EH.
Gambar 24. Kubus dalam Koordinat Ruang Tentukan:
a. besar sudut antara bidang BDE dan BDG. b. besar sudut antara bidang BPQ dan ABCD. c. besar sudut antara bidang DPQ dan bidang BDHF.
T. Persamaan Vektor dari suatu Garis Potong antara Dua Bidang
Perpotongan suatu bidang dengan bidang lain akan menghasilkan suatu garis yang dinamakan dengan garis potong bidang. Ilustrasinya dapat dilihat seperti gambar 25.
Gambar 25. Ilustrasi Perpotongan Dua Bidang
Garis potong bidang dapat disajikan dalam bentuk persamaan vektor. Garis potong bidang dengan suatu persamaan vektor melalui suatu posisi titik dan juga merupakan posisi titik yang dilewati oleh kedua bidang yang berpotongan. Dengan kata lain, posisi titik dimuat oleh dua bidang dan persamaan vektor. Contoh:
Diketahui dua bidang dengan persamaan x3y6z2 dan 2x7y3z7 berpotongan pada suatu garis. Tentukan persamaan vektor garis potong kedua bidang. [Petunjuk: cari dua posisi titik yang dimuat oleh kedua bidang.]
Pembahasan
Kedua bidang akan melalui titik tertentu, sebagai contoh untuk z0. Bidang 2
6
3
y z
x memuat titik
4,2,0
,
1,1,0
, dan titik-titik lainnya pada 0
z . Sedangkan bidang 2x7y3z7 memuat titik
0,1,0
,
7,1,0
, dan berbagai titik lain dengan z0.Dari banyaknya posisi titik yang dilewati oleh bidang x3y6z2 dan 7
3 7
2x y z , hanya ada satu titik yang sama yang dilewati oleh kedua bidang dengan z0. Untuk mengetahui titik tersebut, yaitu dengan cara mensubsitusi
0
z pada kedua persamaan bidang sehingga menjadi
0 7 3 7 2 2 0 6 3 y x y x dan diperoleh 7 7 2 2 3 y x y xDari kedua persamaan tersebut, variable x atau y dieliminasi sehingga diperoleh suatu titik yaitu
7,3,0
. Titik
7,3,0
merupakan suatu titik yang dimuat kedua bidang dan persamaan vektor dari garis potong bidang. Selanjutnya, tinggal satu titik lagi yang diperlukan untuk menentukan persamaan vektor dari garis potong bidang. Untuk menemukan titik tersebut, lakukan langkah yang sama seperti di atas dengan mensubsitusi z1, dan mengeliminasi variabel akan diperoleh suatu titik lain yang dimuat kedua bidang dan persamaan vektor garis potong bidang, yaitu titik
26 6 1
.Jadi persamaan vektor dari garis potong kedua bidang merupakan persamaan vektor yang melalui posisi titik
7 3 0
dan titik
26 6 1
. Dari kedua titik tersebut, diperoleh direction vektor yaitu:
26 6 1
7 3 0
33 9 1
d .
Dengan demikian, persamaan vektor dari garis potong bidang x3y6z2 dan 7 3 7 2x y z bidang adalah
7 3 0
33 9 1
r . Soal latihan1. Dua buah bidang didefinisikan dengan persamaan x2yz4 dan 6
3
y
x . Tentukan persamaan vektor dari garis potong kedua bidang. 2. Dua buah bidang dengan persamaan r
3 1 1
2 dan r
2 5 1
15berpotongan di garis l. a. Tentukan direction garis l
b. Tunjukan bahwa titik dilewati oleh kedua bidang c. Tentukan persamaan vektor garis l.
3. Tunjukan bahwa bidang-bidang dengan persamaan 2x3yz4, 7
4
y z
x , dan 3x10y3z1 berpotongan pada suatu garis. Kemudian tentukan persamaan vektor dari garis potong itu.
DAFTAR PUSTAKA
Gibbs, J.W. (1901). Vector Analysis. USA: Yale University Press.
Goldie, S. (2012).International AS and A Level Mathematics: Pure Mathematics 2 and 3. London: Hodder Education Hachette UK Company.
Learning Express Editors (LEE). (2002). 501 Geometry Questions. USA: Learning Express LLC.
Neill, H., dan Quadling, D. (2002). Advanced Level Mathematics: Pure Mathematics I. United Kingdom: Cambridge University Press.
Neill, H., dan Quadling, D. (2002). Advance Level Mathematics: Pure Mathematics II and III. United Kingdom: Cambridge University Press.
Purcell, E.J., dan Varberg, D. (1997). Kalkulus dan Geometri Analitis Jilid II Edisi V. Jakarta: Erlangga.
Spiegel, M. R., Lipschutz, S., & Spellman, D. (1959). Schaum's outline of theory and problems of vector analysis and an introduction to tensor analysis. USA: McGraw-Hill.