9 BAB III
PERAMBATAN KETIDAKPASTIAN
Deskripsi:
Pada bab ini akan dibahas mengenai konsep perambatan ketidakpastian.
Manfaat:
Memberikan metode yang benar saat melakukan proses pengukuran dan memproses hasil pengukuran.
Relevansi:
Analisis kesalahan adalah studi dan evaluasi ketidakpastian dalam pengukuran. Pengalaman menunjukkan bahwa tidak ada pengukuran dapat benar-benar bebas dari ketidakpastian.
Learning Outcome:
Mahasiswa memahami dan mampu mengimplementasikan perambatan ketidakpastian hasil pengukuran.
MATERI:
Kuantitas fisik yang paling biasa tidak dapat diukur dalam pengukuran langsung tunggal tapi malah ditemukan dalam dua langkah yang berbeda. Sebagai contoh, untuk menemukan luas persegi panjang, Anda benar-benar mengukur panjangnya l dan ketinggian h dan kemudian menghitung luas A sebagai A = lh. Ketika pengukuran melibatkan dua langkah, estimasi ketidakpastian juga melibatkan dua langkah. Pertama-tama kita harus memperkirakan ketidakpastian dalam jumlah diukur secara langsung dan kemudian menentukan bagaimana ketidakpastian ini "merambat" melalui perhitungan untuk menghasilkan ketidakpastian dalam jawaban akhir. Ini perambatan kesalahan adalah subjek utama dari bab ini.
3.1 Pengukuran tak langsung satu kali Misalkan yang akan diukur adalah
x = f(u, v, . . . .)
u, v, . . . diukur langsung satu kali sehingga diperoleh u = 𝑢� + δ𝑢�, v = 𝑣̅ + δ𝑣̅, . . . .
x = 𝑥̅ + δ𝑥̅
10 δ𝑥̅ = ∂∂ 𝑓 𝑢 δ𝑢� + ∂∂ 𝑓 𝑣 δ𝑣̅ + . . . Contoh 1. q = x + …+ z – (u + … + w) 𝑞� = 𝑥 � + . . . 𝑧� - (𝑢� + . . . + 𝑤�) δ𝑞� = δ𝑥 � + . . . + δ 𝑧� + δ𝑢� + . . . + δ𝑤� 2. 𝑞 = 𝐵𝑥 dengan Β adalah tetapan tanpa ketidaktepatan
𝑞� = 𝐵𝑥̅ δ𝑞� = Β δ𝑥̅ 3. 𝑞 = 𝑥𝑛 𝛿𝑞 |𝑞�|= |𝑛| 𝛿𝑥 |𝑥̅|
3.2 Pengukuran taklangsung berulang-ulang ( N kali) Misalkan yang akan diukur adalah
x = f(u, v, . . . .)
u, v, . . . diukur langsung N kali sehingga diperoleh u = 𝑢� + δ𝑢�, v = 𝑣̅ + δ𝑣̅, . . . . x = 𝑥̅ + δ𝑥̅ dengan 𝑥̅ = f(𝑢�, 𝑣,� . . .) dan δ𝑥̅ = � �∂∂ 𝑢 𝑓 δ 𝑢�� �∂∂ 𝑓 𝑢 δ 𝑢�� + �∂∂ 𝑓 𝑣 δ𝑣̅� �∂∂ 𝑓 𝑣 δ𝑣̅� + . . .... Contoh: 1. q = x + …+ z – (u + … + w) 𝑞� = 𝑥 � + . . . 𝑧� - (𝑢� + . . . + 𝑤�) δ𝑞� = { (δ𝑥̅ )P 2 + . . . (δ𝑧̅)2 + (δ𝑢�)2 + . . . + (δ𝑤�)2 }0,5 2. 𝑞 = 𝐵𝑥 dengan Β adalah tetapan tanpa ketidaktepatan
11 𝑞� = 𝐵𝑥̅ δ𝑞� = Β δ𝑥̅ 3. 𝑞 = 𝑥𝑛 𝛿𝑞 |𝑞�|= |𝑛| 𝛿𝑥 |𝑥̅|
4. Ketidakpastian dalam Cosine
Misalkan kita telah mengukur suatu sudut θ sebagai
θ = (20 ± 3)o
dan bahwa kita ingin mencari cos θ. Perkiraan terbaik kami cos θ, tentu saja, cos 20° = 0,94, dan menurut (3.23), ketidakpastian adalah
𝛿(cos 𝜃) = �𝑑cos𝜃𝑑𝜃 � 𝛿𝜃
= |sin𝜃| 𝛿𝜃(𝑑𝑎𝑙𝑎𝑚 rad) Kami telah menunjukkan bahwa δθ harus dinyatakan dalam radian, karena turunan dari cos θ - sin θ hanya jika dinyatakan dalam radian. Oleh karena itu, kita menulis ulang δθ = 3° sebagai δθ = 0,05 rad, kemudian 𝛿(cos𝜃) = (sin20𝑜) x 0,05
= 0,34 x 0,05 = 0,02 Dengan demikian, jawaban akhir kami adalah
Tugas; q = x (y - z sin u)
x, y, z, dan u diukur langsung berulang-ulang. Hitung fungsi sinu, lalu produk dari z dan
sinu,terus perbedaan y dan z sinu, dan akhirnya produk x dan (y - z sinu).
Misalkan Anda mengukur tiga angka sebagai berikut:
x = 200 ± 2, y = 50 ± 2, z = 40 ± 2
dimana tiga ketidakpastian yang independen dan acak. Gunakan perambatan langkah-demi-langkah untuk menemukan kuantitas q = x/(y - z) dengan ketidakpastiannya. [Pertama menemukan ketidakpastian dalam perbedaan y - z dan kemudian quotient x/(y - z).]
12
q = y – x sin y
Fungsi ini adalah perbedaan dari dua istilah, y dan x sin y, tetapi kedua istilah ini pasti tidak independen karena keduanya bergantung pada y. Dengan demikian, untuk memperkirakan ketidakpastian, kita harus memperlakukan istilah sebagai dependen
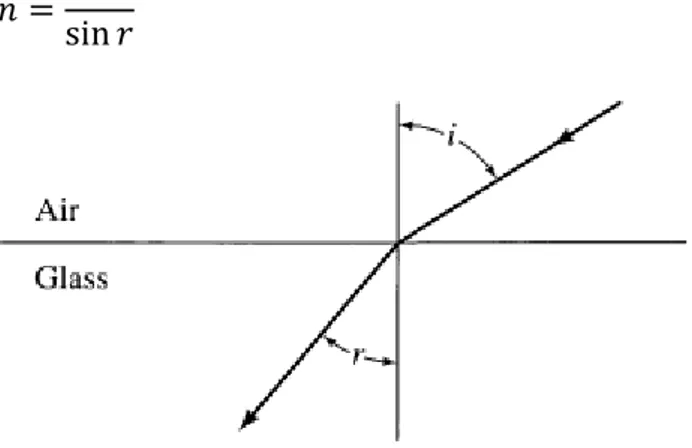
Contoh: Indeks bias Menggunakan Hukum Snell. Jika sinar melewati cahaya dari udara ke kaca, sudut insiden i dan r refraksi didefinisikan seperti pada Gambar 3.5 dan terkait oleh hukum Snell, sin i = n sin r, di mana n adalah indeks bias dari kaca. Jadi, jika Anda mengukur sudut i dan r, Anda dapat menghitung indeks bias n sebagai
𝑛 =sin 𝑟 sin 𝑖
Gambar 3.1 Sudut insiden i dan r refraksi ketika sinar cahaya berpindah dari udara ke dalam gelas
Ketidakpastian dalam jawaban ini mudah dihitung. Karena n adalah hasil sin i dan sin r, ketidakpastian fraksi n adalah jumlah kuadrat dari mereka dalam sin i dan sin r:
𝛿𝑛
𝑛 =��𝛿 sin 𝑖sin 𝑖 �
2
+ (𝛿 sin 𝑟sin 𝑟 )2
Untuk menemukan ketidakpastian pecahan dalam sinus setiap sudut θ, kami mencatat bahwa 𝛿 sin 𝜃 = �𝑑 sin 𝜃𝑑𝜃 � 𝛿𝜃
= | cos 𝜃| 𝛿𝜃 (in rad) Dengan demikian, ketidakpastian pecahan
𝛿 sin 𝜃
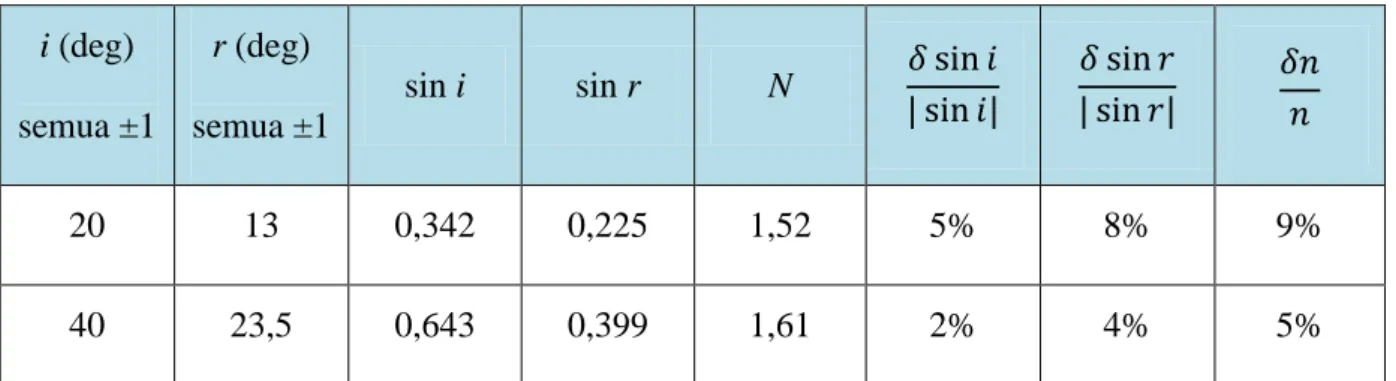
13 Misalkan sekarang kita mengukur sudut r untuk beberapa nilai i dan mendapatkan hasil yang ditunjukkan pada dua kolom pertama dari Tabel 3.1 (dengan semua pengukuran dinilai tidak menentu oleh ± 1°, atau 0,02 rad). Perhitungan n = sin i/sin r mudah dilakukan seperti yang ditunjukkan dalam tiga kolom berikutnya Tabel 3.1. Ketidakpastian dalam n kemudian dapat ditemukan seperti pada tiga kolom terakhir, ketidakpastian pecahan dalam sin i dan sin r dihitung dengan menggunakan (3.32), dan akhirnya ketidakpastian fraksi n ditemukan dengan menggunakan (3.31).
Tabel 3.1. Menemukan indeks bias
i (deg)
semua ±1
r (deg)
semua ±1
sin i sin r N 𝛿 sin 𝑖
| sin 𝑖|
𝛿 sin 𝑟
| sin 𝑟| 𝛿𝑛𝑛
20 13 0,342 0,225 1,52 5% 8% 9%
40 23,5 0,643 0,399 1,61 2% 4% 5%
Sebelum membuat serangkaian pengukuran seperti dua ditunjukkan pada Tabel 3.1, Anda harus berpikir hati-hati bagaimana cara terbaik untuk merekam data dan perhitungan. Sebuah tampilan rapi seperti itu pada Tabel 3.1 membuat pencatatan data lebih mudah dan mengurangi bahaya kesalahan dalam perhitungan.
Kedua contoh hanya diberikan adalah khas dari banyak eksperimen di laboratorium fisika pengantar. Beberapa percobaan membutuhkan perhitungan yang lebih rumit, namun. Sebagai contoh seperti percobaan, saya bahas disini pengukuran percepatan gerobak bergulir menuruni lereng.
14 Gambar 3.2 Sebuah kereta gulungan menuruni lereng θ. Setiap photocell
terhubung ke timer untuk mengukur waktu untuk gerobak untuk lulus
Mari kita mempertimbangkan gerobak bergulir menuruni lereng θ seperti pada Gambar 3.6. Percepatan yang diharapkan adalah g sin θ dan, jika kita mengukur θ, kita dapat dengan mudah menghitung percepatan yang diharapkan dan ketidakpastiannya .Kita dapat mengukur percepatan a yang sebenarnya dengan timing gerobak melewati dua fotosel seperti yang ditunjukkan, masing-masing terhubung ke waktu. Jika gerobak memiliki panjang 1 dan membutuhkan waktu t1 untuk lulus fotosel pertama, kecepatan ada v1 = l/t1. Dengan cara
yang sama, v2 = l/t2. (Tepatnya, kecepatan ini adalah kecepatan rata-rata kereta itu sementara
lewat dua fotosel. Namun, disediakan l kecil, perbedaan antara kecepatan rata-rata dan sesaat tidak penting.) Jika jarak antara fotosel adalah s, maka rumus terkenal v22 = v12 + 2as
menyiratkan bahwa 𝑎 =𝑣222𝑠− 𝑣12 �2𝑠� �𝑙2 𝑡1 22− 1 𝑡12�
Menggunakan formula ini dan nilai yang terukur dari 1, s, t1, dan t2, kita dapat dengan mudah
menemukan percepatan diamati dan ketidakpastiannya
Satu set data untuk percobaan ini, termasuk ketidakpastian, adalah sebagai berikut (angka dalam kurung adalah ketidakpastian persentase yang sesuai, karena Anda dapat dengan mudah memeriksa):
l = (5,00 ± 0,05) cm (1%) s = (100,0 ± 0,2) cm (0,2)%) t1 = (0,054 ± 0,001) s (2%)
t2 = (0,031 ± 0,001) s (3%)
Dari nilai-nilai ini, kita dapat langsung menghitung faktor pertama dalam (3.33) sebagai l2/2s = 0,125 cm. Karena ketidakpastian fraksi 1 dan s adalah 1% dan 0,2%, yang di l2/2s adalah
15 (ketidakpastian fraksi 𝑙2/2s) = �(2𝛿𝑙 𝑙 )2+ ( 𝛿𝑠 𝑠 )2 = �(2 x 1%)2+ (0,2%)2 = 2%
(Perhatikan bagaimana ketidakpastian dalam s tidak membuat kontribusi yang cukup dan bisa saja diabaikan). Oleh karena itu,
𝑙2/2𝑠 = 0,125 cm ± 2%
Karena ketidakpastian pecahan di t1 adalah 2%, dalam l/t12 adalah 4%. Jadi, karena t1 =
0,054 s,
𝑙2
𝑡12 = (343 ± 14) s −2
Dengan cara yang sama, ketidakpastian pecahan di l/t22 adalah 6 % dan
𝑙2
𝑡22 = (1041 ± 62) s −2
Pengurangan ini (dan menggabungkan kesalahan dalam kuadratur), kita menemukan 1 𝑡22− 1 𝑡12 = (698 ± 64) s −2 (atau 9%) Akhirnya, 𝑎 = (0,125 cm ± 2%) x (698 s−2± 9%) = 87,3 cm/s2± 9% atau 𝑎 = (87 ± 8) cm/s2 Tugas: 1. 𝑞 =𝑥+𝑦 𝑥+𝑧 x, y, dan z diukur langsung berulangkali. Laporkan hasil q, 𝑞 = 𝑥2𝑦 − 𝑥𝑦2
ilmuwan mengukur x dan y sebagai berikut:
𝑥 = 3,0 ± 0,1 dan 𝑦 = 2,0 ± 0,1 Apa jawabannya untuk q dan ketidakpastiannya.