Penerapan Generalized Additive Model (GAM)
pada Rata-rata Lama Sekolah Provinsi Jawa Tengah
Rosalinda Nainggolan1, Yudhie Andriyana2, Achmad Bachrudin3 Departemen Statistika, Universitas Padjajaran, Bandung1,2,3
rosalinda16001@mail.unpad.ac.id
ABSTRAK
Untuk mengetahui hubungan antara variabel respon dan variabel prediktor dibutuhkan adanya suatu pemodelan statistika yang tepat. Model statistika merupakan persamaan matematika untuk menggambarkan kondisi nyata suatu set data. Model linier adalah pemodelan statistika yang umum digunakan untuk melihat hubungan antar variabal. Namun model linier memiliki beberapa kelemahan diantaranya yaitu asumsi normalitas pada variabel respon dan hubungan linier antar variabel yang diteliti. Oleh karena kondisi sesungguhnya dapat bertolak belakang, maka Hastie dan Tibshirani (1986) memperkenalkan Generalized Additive Model (GAM). Metode tersebut dapat diaplikasikan pada set data yang tidak membutuhkan asumsi kenonlinearan dalam hubungan antara variabel respon dan prediktor serta tidak membatasi distribusi variabel respon hanya pada distribusi normal saja akan tetapi distribusi-distribusi lain dalam keluarga eksponensial dapat dipergunakan dalam model ini. Selain itu GAM dapat mengontrol sifat smooth suatu kurva, sehingga kurva terhindar dari sifat rigid dan over-fitting. Metode ini akan diterapkan pada data rata-rata lama sekolah terhadap variabel-variabel prediktornya dikarenakan pola hubungan yang terjadi berbeda-beda dan sulit dipresifikasi. Kata kunci: RLS, GAM, Inverse Gaussian
1. PENDAHULUAN
Rata-rata Lama Sekolah (RLS) sebagai salah satu indikator penyusun IPM dapat mencerminkan capaian pendidikan suatu wilayah, baik dari sarana prasarana, akses, hingga kualitas pendidikan. RLS adalah rata-rata jumlah tahun belajar penduduk usia 25 tahun ke atas yang telah diselesaikan dalam pendidikan formal (tidak termasuk tahun yang mengulang) [1]. Dalam upaya peningkatan angka RLS di suatu wilayah tentunya harus diketahui faktor-faktor apa yang mempengaruhi RLS sehingga dapat diambil suatu kebijakan yang tepat sasaran untuk meningkatkan angka RLS seperti rasio beban ketergantungan, rasio murid guru SLTA, rasio murid sekolah SLTA, rasio jenis kelamin, PBRD per kapita, dan persentase penduduk miskin.
Dari enam provinsi yang berada di pulau jawa, dimensi pembentuk IPM provinsi Jawa Tengah yaitu Rata-rata Lama Sekolah (RLS) dan Harapan Lama Sekolah (HLS) menduduki urutan terbawah, Angka Harapan Hidup (AHH) menduduki urutan ke-2, dan pengeluaran per kapita di Jawa Tengah menduduki urutan ke-5. Penjelasan diatas menunjukan bahwa dimensi pendidikan Provinsi Jawa Tengah menduduki posisi terendah dibandingkan dengan lima provinsi lainnya di pulau Jawa. Artinya pemerintah Provinsi Jawa Tengah perlu kerja keras untuk mengejar ketertinggalannya apalagi untuk memenuhi standar rata-rata lama sekolah yang disarankan UNDP sebesar 15 tahun.
Data RLS di Jawa Tengah tahun 2016 terhadap variabel prediktornya menunjukan adanya sebaran yang berbeda-beda. Dari prespesifikasi yang dilakukan melalui scatter plot, sebaran data rasio beban ketergantungan terhadap RLS menunjukan arah menurun, yang mengindikasikan bahwa beban ketergantungan yang rendah menyebabkan persentase RLS yang semakin tinggi. Sebaran rasio murid guru, rasio murid sekolah, dan rasio jenis kelamin terhadap
RLS menunjukan pola yang menyebar, sedangkan PRDB per kapita menumpuk pada sisi kiri bawah. Dengan pola data seperti itu diperlukan fungsi pemulus yang dapat menjadikan kurva mengikuti pola data yang ada.
Pola sebaran data yang sedemikian rupa merupakan permasalahan yang menjadikan metode linear biasa tidak cukup untuk memodelkan data RLS di Jawa Tengah tahun 2016. Perlu adanya metode yang dapat mencakup fungsi pemulus bagi variabel prediktor. Salah satu metode yang dapat menangani hal tersebut adalah melalui metode Generalized Additive Models (GAM). Berdasarkan perumusan masalah diatas, adapun yang menjadi tujuan penelitian ini adalah menerapkan Generalized Additive Models (GAM) untuk memodelkan rata-rata lama sekolah (RLS) tahun 2016 di Provinsi Jawa Tengah. Manfaat dari penerapan ini adalah diperolehnya pengetahuan statistik mengenai Generalized Additive Models (GAM) dalam pemodelan hubungan variabel respon dan beberapa variabel prediktor yang diduga kuat tidak memiliki hubungan linier.
2. METODE PENELITIAN
2.1 Generalized Linear Model (GLM)
Dalam beberapa kasus di lapangan menyatakan bahwa distribusi repson tidak selalu berdistribusi normal, meskipun saling bebas. Kondisi seperti ini dapat diatasi dengan melakukan transformasi dari respon. Nelder dan Wedderburn (1972) mengembangkan model linier yang dikenal dengan Generalized Linear Model (GLM). Model ini mempunyai cakupan distribusi yang lebih luas dibandingkan NLM, yaitu mengasumsikan bahwa respon berdistribusi keluarga eksponensial, termasuk distribusi normal [2].
GLM terdiri dari 3 komponen, yaitu:
1. Komponen acak, menentukan distribusi bersyarat dari variabel respon, dimana 𝑌𝑖 saling bebas atau independen. Distribusi dari 𝑌𝑖 adalah anggota dari keluarga eksponensial, seperti distribusi Normal, Binomial, Poisson, Gamma, atau distribusi dari keluarga Inverse-Gaussian.
2. Prediktor linier,untuk observasi 𝑖, 𝑖 = 1, … , 𝑛, misalkan 𝑥𝑖𝑗 adalah nilai dari variabel penjelas 𝑥𝑗, 𝑗 = 1, … , 𝑝 . Maka 𝑥𝑖 = 𝑥𝑖1, … , 𝑥𝑖𝑝. Prediktor linear dari GLM menghubungkan parameter 𝜂𝑖 berhubungan dengan 𝐸(𝑌𝑖) kepada variabel pejelas 𝑥1, … , 𝑥𝑝 menggunakan kombinasi linear, sehingga 𝜂𝑖 = ∑𝑝𝑗=1𝛽𝑗𝑥𝑖𝑗, 𝑖 = 1, … , 𝑛 . ∑𝑝𝑗=1𝛽𝑗𝑥𝑖𝑗 sebagai prediktor linier yang mencerminkan bahwa persamaan tersebut linier dalam parameter.
3. Fungsi link, yaitu fungsi yang mentransformasikan ekspektasi dari variabel respon, 𝜇𝑖 = 𝐸(𝑌𝑖), 𝑖 = 1, … , 𝑛 dengan prediktor linier. Sehingga model GLM dapat ditulis sebagai berikut:
𝑌𝑖 ~𝑖𝑖𝑑𝐾𝑒𝑙𝑢𝑎𝑟𝑔𝑎 𝐸𝑘𝑠𝑝𝑜𝑛𝑒𝑠𝑖𝑎𝑙(𝜇𝑖, ∅)
dengan 𝑔(𝜇𝑖) = 𝜂𝑖 = 𝛽0+ 𝛽1𝑥𝑖1+ ⋯ + 𝛽𝑝𝑥𝑖𝑝 ; 𝑖 = 1, … , 𝑛 , dan ∅ adalah parameter dispersi.
Kemudian model diatas dapat ditulis kembali dalam bentuk vektor: 𝒀𝑖𝑖𝑑 ~𝐾𝑒𝑙𝑢𝑎𝑟𝑔𝑎 𝐸𝑘𝑠𝑝𝑜𝑛𝑒𝑠𝑖𝑎𝑙(𝝁, ∅) 𝜼 = 𝑔(𝝁) = 𝑿𝛽
Berdasarkan uraian diatas, GLM memiliki keterbatasan yaitu hanya mampu mencocokkan model dengan variabel respon berdistribusi keluarga eksponensial dengan prediktor linier.
2.2 Generalized Additive Model (GAM)
GAM pertama kali dikembangkan oleh Hastie dan Tibshirani pada tahun 1986 (Hastie dan Tibshirani) [3]. GAM merupakan perluasan model aditif umum dengan memodelkan 𝑌 sebagai kombinasi aditif fungsi univariat dari variabel penjelas. Metode ini mengakomodasi adanya pengaruh nonlinear dari variabel prediktor tanpa harus mengetahui bentuk pengaruh secara eksplisit. Pengaruh nonlinear tersebut dapat diperbaiki dengan melakukan pemulusan pada struktur hubungan antara variabel respon dan variabel prediktor.
Selain merupakan perluasan dari model aditif GAM juga perluasan dari GLM yang mengasumsikan variabel respon 𝑌 berdistribusi keluarga eksponensial yang memiliki fungsi kepekatan peluang:
𝑓(𝑦𝑖; 𝜃𝑖; 𝜙) = 𝑒𝑥𝑝 (𝑦𝑖𝜃𝑖− 𝑐(𝜃𝑖)
𝑎(𝜙) + 𝑑(𝑦𝑖, 𝜙))
dimana 𝜃𝑖 disebut parameter kanonik dan disebut 𝜙 disebut parameter dispersi. Jika 𝑎(𝜙) = 1, 𝑑(𝑦𝑖, 𝜙) = 𝑑(𝑦𝑖), maka dimiliki bentuk natural distribusi keluarga eksponensial 𝑓(𝑦𝑖; 𝜃𝑖) = 𝑒𝑥𝑝 𝑑(𝑦𝑖) exp [𝑦𝑖𝜃𝑖− 𝑐(𝜃𝑖)]. 𝐸(𝑦𝑖|𝑥𝑖) = 𝜇𝑖 = 𝑐′(𝜃
𝑖), ini menyatakan hubungan yang penting antara 𝜃𝑖 dan 𝜇𝑖 yaitu 𝜃𝑖 =(𝑐′)−1(𝜇𝑖)= 𝑔(𝜇𝑖) kemudian dihubungkan dengan variabel prediktor melalui fungsi penghubung (link function) 𝜂𝑖, sehingga diperoleh bentuk umum GAM adalah sebagai berikut:
𝑌𝑖 ~𝑖𝑖𝑑𝐸𝐹(𝜇𝑖, ∅)
𝑔(𝜇𝑖) = 𝜂𝑖 = 𝛽0+ 𝑓1(𝑥𝑖1) + ⋯ + 𝑓𝑗(𝑥𝑖𝑗) + 𝜖𝑖; 𝑖 = 1,2, … 𝑛 ; 𝑗 = 1,2, … , 𝑝 (1) dimana 𝑓𝑗 adalah fungsi penghalus nonparametrik pada kovariat 𝑥𝑗, untuk 𝑗 = 1, . . . , 𝑝 dan 𝐸𝐹 menunjukkan berasal dari distribusi keluarga eksponensial. Persamaan (1) juga dapat dituliskan secara umum sebagai:
𝑔(𝜇) = 𝜂 = 𝛽0+ ∑𝑝𝑗=1𝑓𝑗(𝑋𝑗)+ 𝜀 ; 𝑗 = 1,2, … , 𝑝
Regresi Kubik Splines
Menurut Fan dan Yao [4] Splines merupakan potongan polinomial yang tersegmen terhubung pada titik yang menunjukkan terjadinya perubahan-perubahan perilaku kurva pada interval-interval yang berbeda. Titik penghubung tersebut disebut knot. Secara umum spline dengan orde m=0,1,2, dan 3 yang masing-masing disebut constant, linier, quadratic dan cubic. Sehingga fungsi cubic spline dengan titik-titik knot 𝑘1, 𝑘2, … , 𝑘𝑠 , secara umum dapat disajikan sebagai berikut:
𝑓(𝑥𝑖) = 𝛽0+ 𝛽1𝑥𝑖+ ⋯ + 𝛽𝑚𝑥𝑖𝑚+ ⋯ + 𝛽𝑚𝑠(𝑥𝑖− 𝑘𝑠)+𝑚 untuk 𝑖 = 1,2, … , 𝑛
Maka secara umum, jika dimiliki model 𝑌 = 𝑓(𝑥) + 𝜖, fungsi cubic spline diformulasikan:
𝑓(𝑥) ≈ ∑ 𝑏𝑘(𝑥)𝛽𝑘 𝑠
𝑘=1
Dimana s adalah banyaknya knot; 𝑏𝑘(𝑥) adalah fungsi basis ke-k untuk regresi spline kubik, dan 𝛽𝑘 adalah parameter yang tidak diketahui. Sehingga 𝑓′′(𝑥) = ∑𝑠𝑘=1𝑏𝑘′′(𝑥)𝛽𝑘 = 𝒃′′(𝑥)𝑇𝜷
Dimana 𝒃′′(𝑥) adalah vektor turuan kedua dari fungsi basis. Ketika 𝑓′′(𝑥) adalah skalar maka akan sama dengan nilai transposenya, sehingga
[𝑓′′(𝑥)]2= 𝜷𝑇𝒃′′(𝑥)𝑇
𝒃′′(𝒙)𝜷 = 𝜷𝑇𝑺(𝑥)𝜷 (2)
Oleh karenanya 𝑱(𝑓) = 𝜷𝑇∫ 𝑺(𝑥)𝑑𝑥 𝜷 = 𝜷𝑇𝑯 𝜷 , sehingga dengan dimilikinya suatu basis, kita akan selalu dapat mengevaluasi matrik koefisien 𝑯 yang mengijinkan penalti 𝑱(𝑓)
ditulis sebagai bentuk kudratik dari vektor 𝒃 (dimana matriks 𝑯 tidak bergantung pada nilai 𝒃). Kemudian masalah estimasi adalah dapat dicapai dengan meminimumkan
∑{𝑦𝑖− 𝑓(𝑥𝑖)}2+ 𝜆 ∫ 𝑓′′(𝑥)2 𝑛
𝑖=1
Dimana 𝜆 adalah parameter yang mengatur perimbangan (trade-off) antara data dan kemulusan model. Memilih basis untuk 𝑓 menjadikan desain matrik 𝑿 dan matriks penalti 𝑯 dihitung seperti yang dijelaskan sebelumnya. Sehingga permasalahan fitting dapat ditulis:
‖𝒚 − 𝑿𝒃‖2+ 𝜆𝜷𝑇𝑯 𝜷 Generalized Additive Model Cubic Splines
Model umum GAM pada persamaan (1.4) dan Cubic Spline untuk satu variabel pada persamaan (1.5), ditulis kembali 𝑔(𝜇) = 𝜂 = 𝛽0+ ∑𝑝𝑗=1𝑓𝑗(𝑋𝑗)+ 𝜀 ; 𝑗 = 1,2, … , 𝑝 , maka dengan menginput unsur basis maka dapat dituliskan menjadi:
𝑔(𝜇) = 𝜂 = 𝛽0+ ∑ 𝑏𝑘(𝑥)𝛽𝑘 𝑙1 𝑘=1 + ⋯ + ∑ 𝑏𝑘(𝑥)𝛽𝑘 𝑙𝑗 𝑘=1 + 𝜀 ; 𝑗 = 1,2, … , 𝑝 (3) Kemudian model diatas dapat ditulis kembali dalam bentuk vektor:
𝒀𝑖𝑖𝑑 ~𝐾𝑒𝑙𝑢𝑎𝑟𝑔𝑎 𝐸𝑘𝑠𝑝𝑜𝑛𝑒𝑠𝑖𝑎𝑙(𝝁, ∅)
𝜼 = 𝑔(𝝁) = 𝑿𝛽
𝑿 adalah desain matriks untuk model aditif yang dibentuk seperti pada persamaan (3) dengan menggunakan pemulus, 𝑔 adalah fungsi link pemulus monoton. Kemudian permasalahan fitting diatas dapat diselesaikan dengan memaksimumkan penalized-log likelihood [5]:
𝑙∗= 𝑙(𝒚; 𝜷) −1
2∑ 𝜆𝑗𝜷𝑗𝑇𝑯𝒋 𝜷𝒋 𝑝
𝑗=1
Dimana 𝜆𝑗> 0 dan 𝑙(𝒚; 𝜷) = ∑𝑛𝑖=1{[𝑦𝑖𝜂𝑖+ 𝑐(𝜂𝑖)] + 𝑑(𝑦𝑖)}, 𝜂𝑖 adalah elemen ke-𝑖 dari 𝑔(𝜇) =𝜂 dan menurut persamaan (2) 𝑯𝒋= ∫ 𝒃′′(𝑥)𝑇𝒃′′(𝒙). Wood (2002) menyatakan solusi untuk memaksimumkan penalized likelihood dapat dicapai dengan menggunakan iteratively re-weighted least square (IRLS) sehingga diperoleh nilai estimasi 𝜷̂ [5] :
𝜷[𝑡+1]=
{[
𝑿𝑻𝑾[𝑡]𝑿 −𝑺]
−1𝑿𝑻𝑾[𝑡]𝒛[𝑡]}
dengan 𝑾[𝑡]
adalah matriks penimbang yang mempunyai elemen 𝑤
𝑖𝑖∝
1𝑉(𝜇𝑖[𝑡])𝑔′(𝜇𝑖[𝑡])
, 𝑺 =
𝑏𝑙𝑜𝑐𝑘𝑑𝑖𝑎𝑔(0, 𝜆
1𝑯
1, … , 𝜆
𝑝𝑯
𝒑), dan
𝒛[𝑡]= 𝑿
𝜷[𝒕]+ 𝑔′ (𝜇
𝑖[𝑡]) (𝒚 − 𝝁
𝒕)
Tahapan Penelitian
Tahapan penelitian yang dilakukan untuk menyelesaikan tujuan penelitian adalah sebagai berikut:
1. Mempersiapkan data, yaitu menentukan variabel respon dan variabel prediktor yang akan digunakan.
2. Membuat scatter plot yang menjelaskan hubungan antar variabel respon dan variabel prediktor.
3. Menentukan distribusi bagi variabel respon secara empiris dengan nilai AIC terkecil dari seluruh pilihan distribusi yang berada pada rentang (0,tak hingga)[6]. Dengan dasar AIC terkecil hasil pemodelan diyakini adalah model terbaik.
4. Menentukan prespesifikasi model berdasarkan pola data pada scatter plot. 5. Pembentukan model melalui tahapan:
a. Membentuk basis pada masing-masing prediktor dengan knot fixed. b. Basis yang terbentuk pada setiap variabel prediktor diberikan penalti.
c. Mengkombinasikan setiap variabel prediktor yang sudah diberikan perlakuan pemulusan sehingga terbentuk model Generalized Additive Model (GAM) cubic spline.
6. Mengestimasi parameter koefisien model bagi setiap variabel prediktor. 7. Memilih model terbaik berdasarkan ukuran AIC dan MSE terkecil.
3. HASIL PENELITIAN DAN PEMBAHASAN
3.1 Sumber Data
Data yang digunakan dalam penelitian ini adalah data sekunder yang diperoleh dari publikasi Badan Pusat Statistika (BPS) tahun 2016. Pada penelitian ini yang dijadikan unit observasi adalah Kabupaten/Kota di Provinsi Jawa Tengah sebanyak 35 Kabupaten/Kota. Data yang digunakan adalah RLS sebagai variabel respon (𝑌) dan faktor-faktor pendukung seperti rasio beban ketergantungan, rasio murid guru SLTA, rasio jenis kelamin, rasio murid sekolah SLTA, PBRD per kapita, dan persentase penduduk miskin di kabupaten/kota di Provinsi Jawa Tengah sebagai variabel prediktor (𝑋).
3.2 Rata-Rata Lama Sekolah
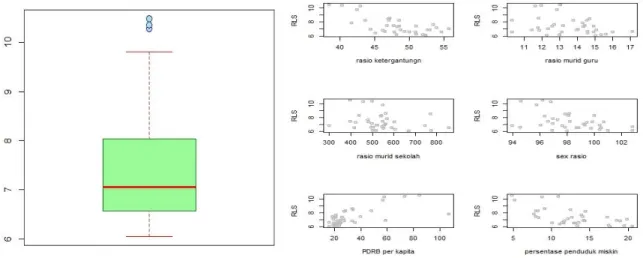
Rata-rata lama sekolah adalah jumlah tahun belajar penduduk usia 25 tahun ke atas yang telah diselesaikan dalam pendidikan formal (tidak termasuk tahun yang mengulang) [1]. Rata-rata angka RLS di Jawa Tengah adalah sebesar 7,45 tahun. Artinya penduduk yang berusia 25 tahun keatas di Jawa Tengah rata-rata lama bersekolah 7 sampai dengan 8 tahun. Namun terdapat tiga kota yang nilainya jauh berada diatas nilai kabupaten/kota yang lain. Ketiga kota tersebut adalah kota Magelang, kota Surakarta dan kota Semarang , dengan angka masing-masing sebesar 10,29 , 10,37, dan 10,49 tahun.
(a) (b)
Gambar 1. a) Boxplot Rata-rata lama sekolah ; b) scatter plot hubungan variabel eksplantori dan variabel respon
3.3 Pemodelan
Pemodelan Generalized Additive Models (GAM) dilakukan dengan terlebih dahulu mengetahui apakah suatu variabel respon mengikuti distribusi keluarga eksponensial. Sesuai dengan tahapan penelitian akan untuk mengetahui variabel respon berdistribusi keluarga eksponensial adalah dengan menggunakan cara pembentukan model regresi sederhana melalui distribusi yang akan memberikan Akaike Information Criterion (AIC) terkecil [6]. Adapun hasil olah diperoleh hasil seperti pada tabel 1.
Tampak bahwa distribusi Inverse Gaussian memberikan hasil AIC terkecil, mengindikasikan bahwa variabel respon mengikuti distribusi inverse gaussian akan memberikan hasil model yang terbaik. Inverse Gaussian adalah distribusi yang termasuk dalam distribusi keluarga eksponensial sehingga metode GAM dapat diterapkan pada data.
Selanjutnya adalah menetapkan knot untuk masing-masing variabel preditor. Karena dilakukannya penalized regression spline maka permasalahan penempatan knot dapat dihindari [5]. Dalam hal ini penulis menentapkan knot bagi setiap variabel prediktor adalah sama yaitu sebanyak 4 knot equidistant. Penetapan knot disini akan dilanjutkan dengan optimasi pada nilai penalti yaitu parameter pemulus untuk setiap variabel prediktor. Kemudian pemodelan GAM dapat dilakukan yang selanjutnya akan diperoleh nilai nilai estimasi 𝜷̂.
Tabel 1. Ukuran AIC dari model regresi berdasarkan distribusi respon dengan rentang [0, ∞]
Distribusi AIC Inverse Gaussian 81,5428 Weibull 85,5407 Gamma 86,0569 Log Normal 86,2892 Inverse Gamma 86,5491 Generalized Gamma 87,3044
Generalized Inverse Gaussian 88,1313
Normal 91,2495
Exponential 223,9910
Pareto 226,2534
Pada penelitian ini selain menerapkan Generalized Additive Models (GAM) dilakukan pula pemodelan dengan menggunakan metode Normal Linear Model (NLM) dan Generalized Linear Model (GLM) sebagai perbandingan. Adapun hasil pemodelan ditunjukan pada tabel dibawah:
Table 2. Nilai MSE dan R-Square pada reduced model
Metode MSE R-Square AIC
(1) (2) (3) (4)
LM 0,5602 0,62222 89,0412
GLM 0,4400 0,74830 79,8673
GAM 0,2856 0,85730 71,7458
Tabel 2. Menunjukkan bahwa GAM adalah model terbaik berdasarkan ukuran-ukuran pemilihan model. Melalui prosedur stepwise, hanya empat variabel saja yang dapat dimasukkan ke dalam model GAM yang terbentuk. Ke-empat variabel tersebut adalah rasio beban ketergantungan, rasio murid guru pada tingkat SLTA, rasio jenis kelamin, dan PDRB per kapita
Dalam Eubank (1988) disebutkan bahwa ukuran kinerja penduga fungsi regresi dapat ditentukan diantaranya dengan rataan kuadrat sisaan (MSE) [7]. Tampak bahwa MSE terkecil dihasilkan dengan menggunakan metode Generalized Additive Models yaitu sebesar 0,2856. R-Square yang dihasilkan juga lebih besar dari kedua metode lainnya yaitu sebesar 0,8573, artinya bahwa ke-empat variabel yang masuk dalam model mampu menjelaskan hubungannya terhadap rata-rata lama sekolah sebesar 85,73%.
4. KESIMPULAN
Pada penelitian ini disimpulkan bahwa kinerja Generalized Additive Models lebih optimal dibandingkan dengan Generalized Linear Model dan Linear Model. Ini dibuktikan perbandingan nilai MSE Generalized Additive Models lebih kecil daripada MSE Generalized Linear Model dan Linear Model. Ini dikarenakan pendekatan Generalized Additive Models dapat mengatasi data yang mempunyai sebaran tidak linier dan variabel respon yang berdistribusi keluarga eksponensial.
Adapun yang menjadi saran untuk penelitian selanjutnya adalah dapat membandingkan beberapa basis pemulus untuk mendapatkan model yang terbaik dan dapat pula mempertimbangkan adanya pengaruh dari parameter scale dan shape dalam hal ini adalah varians dan skewness serta kurtosis dengan menggunakan metode Generalized Additive Model Location, Scale and Shape (GAMLSS)
5. DAFTAR PUSTAKA
[1] http://ipm.bps.go.id/page/ipm
[2] Nelder, J.A. dan Wedderburn, R.W.M., Generalized linear models, Journal of the Royal Statistical Society, A135, 370-384. 1972
[3] Hastie, T. J. dan Tibshirani. “Generalized Additive Model 4th ed”. Chapman dan Hall, London. 1990
[4] Fan, J dan Yao, Q. “Nonliniear Time Series Nonparametric and Parameteric Method. Canada: Springer Science. 2005
[5] Wood, Simon N dan Augustin, Nicole H., “GAMs with integrated model selection using penalized regression splines and applications to environmental modelling”. Ecological Modelling 157 pp 157-177. 2002
[6] Stasinopoulos DM, Rigby RA,et al, “Flexible Regression and Smoothing Using GAMLSS in R”, CRC Press. 2017
[7] Eubank, R.”Spline Smoothing and Nonparametric Regression”. Marcel Dekker, New York. 1988
![Tabel 1. Ukuran AIC dari model regresi berdasarkan distribusi respon dengan rentang [0, ∞]](https://thumb-ap.123doks.com/thumbv2/123dok/4523524.3279493/6.893.252.645.502.784/tabel-ukuran-model-regresi-berdasarkan-distribusi-respon-rentang.webp)