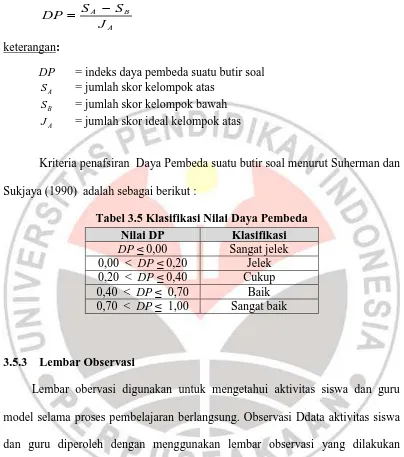
PENERAPAN ACCELERATED LEARNING DALAM PENINGKATAN KEMAMPUAN PENALARAN DAN KOMUNIKASI MATEMATIS SISWA SEKOLAH MENENGAH PERTAMA.
Teks penuh
Gambar


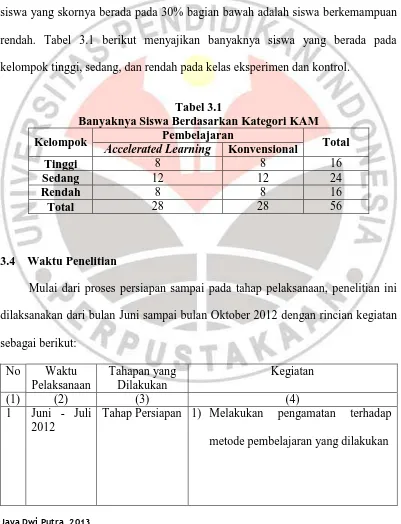

Dokumen terkait
bahwa berdasarkan pertimbangan sebagaimana dimaksud dalam huruf a, perlu menetapkan Keputusan Kepala Badan Karantina Ikan, Pengendalian Mutu dan Keamanan Hasil
PENGALIHAN HAK ATAS PEMILIKAN RUMAH TEMPAT TINGGAL ATAU HUNIAN OLEH ORANG ASING YANG BERKEDUDUKAN DI INDONESIA.. DAFTAR HARGA MINIMAL PEMBELIAN RUMAH TUNGGAL ATAU SATUAN
Pembabatan hutan di Indonesia berdasarkan situs kompasiana yang diakses 20 April 2015, setiap tahun sekitar 1.3 juta hektare hutan mengalami kerusakan(FAO, 2012),
Sehingga dengan jumlah hasil panen yang tinggi serta kualitas buah yang bagus, maka dapat diperoleh keuntungan.Namun, ada beberapa hal yang sangat berpengaruh terhadap produksi
Teknologi Komunikasi adalah segala hal yang berkaitan dengan penggunaan alat bantu untuk memproses dan mentransfer data dari perangkat yang satu ke lainnya.. Berbasis
dan Politik Dalam Negeri di Pemerintah Kota Semarang pada tahun 2015,.. dilaksanakan melalui program penunjang dan program pelaksanaan urusan. Program pelayanan
antara lain tentang teori nilai dan harga, kegiatan produksi untuk.. memenuhi kebutuhan adalah bersifat alamiah, teori uang
Compare the effect of instructional strategy (problem-based learning versus supervised study) with regard to secondary agriculture students’ critical thinking ability and content