PENYELESAIAN PERSAMAAN PENDULUM NONLINEAR DENGAN MENGGUNAKAN METODE DEKOMPOSISI ADOMIAN DAN METODE PERTUBASI HOMOTOPI TUGAS AKHIR.

PENYELESAIAN PERSAMAAN PENDULUM NONLINEAR

DENGAN MENGGUNAKAN METODE DEKOMPOSISI

ADOMIAN DAN METODE PERTUBASI HOMOTOPI

TUGAS AKHIR

Diajukan Sebagai Salah Satu Syarat Untuk Memperoleh Gelar Sarjana Sains Pada

Jurusan Matematika

Oleh:

RATIH NOVA LIS NANI

10554001591

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI SULTAN SYARIF KASIM RIAU

PEKANBARU

xi

PENYELESAIAN PERSAMAAN PENDULUM NONLINEAR

DENGAN MENGGUNAKAN METODE DEKOMPOSISI

ADOMIAN DAN METODE PERTUBASI HOMOTOPI

RATIH NOVA LIS NANI

NIM: 10554001591

Tanggal Sidang: 5 Mei 2010 Periode Wisuda: Juli 2010

Jurusan Matematika Fakultas Sains dan Teknologi

Universitas Islam Negeri Sultan Syarif Kasim Riau Jl. HR. Soebrantas No.155 Pekanbaru

ABSTRAK

Skripsi ini membahas tentang penyelesaian persamaan pendulum nonlinear _{sin 0} 2 2 = + θ θ l g dt d

berdasarkan nilai awal θ(t)=c1 dan 2 '

) (t =c

θ dengan menggunakan metode dekomposisi Adomian dan metode pertubasi homotopi dengan komponen nonlinear Nθ =sinθ. Tujuan dari kedua metode ini adalah untuk memperoleh penyelesaian eksak dari persamaan diferensial pendulum nonlinear tersebut. Berdasarkan perhitungan terlihat bahwa hasil yang diperoleh dengan menggunakan metode dekomposisi Adomian adalah :

L + + + + = 0 0 4 0 2 2 1 sin cos ! 4 sin 2 ) ( θ θ θ θ t l g t l g tc c t

dan hasil yang diperoleh dengan menggunakan metode pertubasi homotopi adalah :

L +         − +         − + = ! 3 3 ! 3 ) 0 ( ) ( 1 2 0 1 3 0 0 θ θ θ θ θ θ θ l g l g t

Kata Kunci : Metode Dekomoposisi Adomian, Metode Pertubasi Homotopi, Persamaan

xii

ON THE SOLUTION OF NONLINEAR PENDULUM EQUATION

BY USING ADOMIAN DECOMPOSITION METHOD AND

HOMOTOPY PERTURBATION METHOD

RATIH NOVA LIS NANI

NIM: 10554001591

Date of Final Exam: May 5th, 2010 Graduation Ceremony Priod: July, 2010

Mathematic Department Faculty of Sciences and Technology

State Islamic University of Sultan Syarif Kasim Riau Soebrantas Street No.155 Pekanbaru

ABSTRACT

This paper discusses the solving of nonlinear pendulum differential equation sin 0

2 2 = + θ θ l g dt d

based on the initial value problem θ(0)=c₁ and ' ₂ ) 0 ( =c

θ by using Adomian decomposition method and homotopi perturbation method with the nonlinear term Nθ =sinθ. Aim of the both of this method is to obtain exact solution of the nonlinear pendulum differential equation. Based on the calculation that the result obtained by using Adomian decomposition method is :

L + + + + = 0 0 4 0 2 2 1 sin cos ! 4 sin 2 ) ( θ θ θ θ t l g t l g tc c t

and the result obtained by using homotopy perturbation method is :

L +       − +       − + = ! 3 3 ! 3 ) 0 ( ) ( 1 2 0 1 3 0 0 θ θ θ θ θ θ θ l g l g t

Keyword: Adomian Decomposition Method, Homotopy Perturbation Method, Nonlinear

xiii

DAFTAR ISI

Halaman

LEMBAR PERSETUJUAN... ii

LEMBAR PENGESAHAAN ... iii

LEMBAR HAK ATAS KELAYAAN INTELEKTUAL ... iv

LEMBAR PERNYATAAN ... v LEMBAR PERSEMBAHAN ... vi ABSTRAK ... vii ABSTRACT ... viii KATA PENGANTAR ... ix DAFTAR ISI ... xi

DAFTAR GAMBAR ... xiii

DAFTAR LAMBANG ... xiv

DAFTAR SINGKATAN... xv

DAFTAR LAMPIRAN ... xvi

BAB I PENDAHULUAN

1.1Latar Belakang ... I-1 1.2Rumusan Masalah ... I-3 1.3Batasan Masalah ... I-3 1.4Tujuan ... I-3 1.5Manfaat... I-3 1.6 Sistematika Penulisan ... I-4

BAB II LANDASAN TEORI

2.1 Persamaan Diferensial ... II-1 2.2 Persamaan Diferensial Nonlinear Orde Dua ... II-2 2.3 Persamaan Diferensial Pendulum ... II-5 2.4 Metode Dekomposisi Adomian ... II-7 2.5 Metode Pertubasi Homotopi ... II-12 2.6 Maple ... II-13

xiv BAB IV ANALISA DAN PEMBAHASAN

4.1 Penyelesaian dengan Metode Dekomposisi Adomian .... IV-1 4.2 Penyelesaian dengan Metode Pertubasi Homotopi ... IV-7

BAB V PENUTUP

5.1 Kesimpulan ... V-1 5.2 Saran ... V-1

DAFTAR PUSTAKA LAMPIRAN

BAB I

PENDAHULUAN

1.1 Latar Belakang

Matematika merupakan salah satu ilmu pengetahuan yang banyak memberikan landasan teori bagi perkembangan teknologi. Matematika senantiasa dikaji dan dikembangkan agar dapat dimanfaatkan di dalam aspek penerapannya. Masalah – masalah dalam dunia nyata dapat lebih mudah dimengerti dengan menggunakan pendekatan matematika.

Cabang dari matematika modern yang mempunyai cakupan wilayah penelitian teoritik dan aplikasi luas adalah persamaan diferensial. Dalam berbagai masalah fisik dan geometri yang melibatkan dua fungsi atau lebih peubah bebas sangat berkaitan dengan persamaan diferensial. Untuk masalah fisik yang paling sederhana dapat di modelkan dengan persamaan diferensial biasa, sedangkan masalah fisik yang lain seperti mekanika fluida, mekanika padat, teori elektromagnetik, teori potensial, difusi dan sebagainya merupakan masalah – masalah fisik yang harus dimodelkan dengan persamaan diferensial parsial.

Umumnya persamaan diferensial orde satu yang linear dapat diselesaikan secara analitik sehingga menghasilkan penyelesaian eksak, sedangkan persamaan nonlinear sangat sulit diselesaikan secara analitik walaupun sebagian kecil dapat diselesaikan dengan metode variabel terpisah.

Umumnya penyelesaian persamaan diferensial nonlinear dilakukan dengan teknik pelinearan, pertubasi. Hal ini akan berdampak pada munculnya galat. Skripsi ini, akan diusulkan dua teknik metode yang digunakan untuk menyelesaikan persamaan diferensial nonlinear, tanpa melakukan linearisasi persamaan, yaitu metode dekomposisi Adomian dan metode pertubasi homotopi.

Metode dekomposisi diperkenalkan pertama kali oleh Adomian pada tahun 1994 yang digunakan untuk menyelesaikan persamaan – persamaan fungsional linear dan nonlinear, seperti persamaan diferensial aljabar, persamaan diferensial biasa, persamaan diferensial parsial, persamaan diferensial integral.

Metode pertubasi homotopi dikenal pada tahun 2004 oleh J. He yang digunakan untuk menyelesaikan persamaan-persamaan linier dan nonlinier. Metode pertubasi homotopi ini digunakan untuk mengecilkan atau menurunkan suatu masalah yang sulit menjadi masalah yang mudah untuk diselesaikan.

Salah satu bentuk persamaan diferensial nonlinear orde dua adalah

persamaan pendulum nonlinear ₂ sin 0

2 = +

θ

θ

l g dt d . Persamaan pendulum

nonlinear ini sangat sulit dan tidak mungkin diselesaikan secara analitis.

Berdasarkan hal tersebut di atas penulis tertarik untuk mengkaji tentang penggunaan metode dekomposisi Adomian dan metode pertubasi homotopi untuk menentukan solusi eksplisit persamaan diferensial nonlinear orde dua, sehingga dalam penulisan skripsi ini penulis mengambil judul ”Penyelesaian Persamaan

Pendulum Nonlinear dengan Menggunakan Metode Dekomposisi Adomian

dan Metode Pertubasi Homotopi”.

1.2 Rumusan Masalah

Rumusan masalah pada skripsi ini adalah bagaimana menentukan penyelesaian persamaan diferensial pendulum ₂ sin 0

2 = +

θ

θ

l g dt d , berdasarkan nilai awal

θ

(0)=c1 dan 2

'

) 0

( =c

θ

dengan menggunakan metode dekomposisi Adomian dan metode pertubasi homotopi.

1.3 Batasan Masalah

Skripsi ini penulis hanya membatasi pada persamaan pendulum nonlinear

orde dua dengan persamaan umumnya ₂ sin 0

2 = +

θ

θ

l g dt d

dengan variabel bebas t berdasarkan nilai awal

θ

(0)=c1 dan 2

'

) 0

( =c

1.4 Tujuan

Tujuan penulisan skripsi ini adalah menentukan solusi persamaan

pendulum nonlinear dengan metode dekomposisi Adomian dan metode pertubasi

homotopi.

1.5 Manfaat

Manfaat dari penelitian ini adalah :

1. Dapat menentukan nilai simpangan sudut pendulum.

2. Dapat menentukan nilai perioda atau frekuensi dari sistem gerak nonlinear.

1.6 Sistematika Penulisan

Sistematika penulisan skripsi ini terdiri dari beberapa bab, yaitu :

BAB I Pendahuluan

Bab ini berisi latar belakang masalah, rumusan masalah, batasan masalah, tujuan, manfaat penelitian, sistematika penulisan.

BAB II Landasan Teori

Bab ini berisikan landasan teori seperti : persamaan diferensial, persamaan diferensial nonlinear orde dua, persamaan pendulum nonlinier, metode dekomposisi adomian, metode pertubasi homotopi, dan Maple.

BAB III Metodologi

Bab ini berisikan studi literatur yang digunakan penulis dan berisikan langkah – langkah yang digunakan untuk mencapai tujuan dari skripsi ini.

BAB IV Pembahasan

Bab ini berisikan tentang perbandingan metode dekomposisi Adomian dan metode pertubasi homotopi yang digunakan untuk membahas persamaan diferensial pendulum nonlinier.

BAB V Penutup

Bab ini berisikan kesimpulan dari seluruh uraian dan saran – saran untuk pembaca.

BAB II

LANDASAN TEORI

Bab ini membahas tentang persamaan diferensial, persamaan diferensial nonlinear orde dua, persamaan pendulum, metode dekomposisi Adomian, dan metode pertubasi homotopi serta Maple.

2.1 Persamaan diferensial

Persamaan diferensial diperoleh berdasarkan pemodelan matematika dari permasalahan yang ada dalam kehidupan sehari – hari. Sebagai contoh penerapan matematika pada ilmu fisika. Misalnya pemodelan matematis yang berasal dari hukum Newton II yang menyatakan, bahwa massa kali percepatan suatu benda sama dengan gaya luar yang bekerja pada benda itu. Suatu benda bermassa m bergerak sepanjang sumbu y pada sistem koordinat kartesius. Hukum Newton II

dapat ditulis sebagai F

dt y d

m ₂ =

2

, dengan F melambangkan gaya luar yang

bekerja pada benda itu. Persamaan tersebut merupakan persamaan diferensial karena memuat turunan dari fungsi yang tidak diketahui y(t) dengan y sebagai variabel terikat yang tergantung pada variabel bebas t . Jadi persamaan diferensial adalah persamaan yang mengandung fungsi dan bentuk – bentuk turunannya.

Jika persamaan diferensial mempunyai satu variabel tak bebas dari persamaan tersebut disebut persamaan diferensial biasa, dan jika persamaan diferensial mempunyai lebih dari satu variabel bebas dan tak bebas dari persamaan tersebut disebut persamaan diferensial parsial.

Orde dari persamaan diferensial adalah orde dari turunan tertinggi dalam persamaan. Bentuk umum dari persamaan diferensial orde satu adalah

0 ) ' , , (t θ θ = F

persamaan diferensial orde dua 0 ) " , ' , , (t θ θ θ = F

0 ) , , ' , , (t n = F

θ

θ

K

θ

dengan F adalah fungsi riil dari t,

θ

,

θ

',K,

θ

n _.

Persamaan diferensial orde n dikatakan linear jika persamaannya dapat ditulis dalam bentuk

) ( ) ( ' ) ( ) ( ) (t a ₁ t 1 a₁ t a₀ t f t a_n θn + _n− θn− +K+ θ + θ = _(2.1) ) ( ), ( ), ( . 0 ) (t a0 t a1 t a 1 t

an ≠ K n− adalah fungsi yang tidak diketahui dari t yang disebut koefisien, dan koefisien dari suatu persamaan diferensial dapat berbentuk konstanta atau variabel.

Persamaan (2.1) dikatakan homogen jika f(t)=0 dan dikatakan nonhomogen jika f(t)≠0. Persamaan yang tidak dapat dinyatakan seperti persamaan (2.1) disebut persamaan nonlinear.

Solusi dari persamaan diferensial biasa adalah fungsi yang jika disubtitusikan pada persamaan diferensial tersebut akan memberikan suatu identitas yang biasa disimbolkan dengan θ =θ(t).

2.2 Persamaan Diferensial Nonlinear Orde Dua

Persamaan diferensial orde dua sering timbul dalam permasalahan fisika. Persamaan diferensial orde dua yang akan dibahas adalah persamaan diferensial nonlinear. Persamaan diferensial nonlinear adalah suatu persamaan yang mengandung variabel tak bebas atau derivatifnya dalam bentuk nonlinear, atau terdapat perkalian antara variabel tak bebas dan derivatifnya.

Secara umum persamaan diferensial orde dua nonlinear sangat sulit untuk mencari solusinya. Persamaan tersebut meliputi turunan kedua, hal tersebut akan mungkin menyelesaikannya dengan melinearkan persamaan tersebut atau dengan dua kali anti diferensial, dengan mereduksi persamaan orde dua menjadi dua persamaan orde satu. Bentuk persamaan diferensial orde dua

) , , ( 2 2 dt d t f dt d θ _{= θ} θ

) , ( , f v d dv v dt d _θ θ θ _{= =} (2.2)

menggunakan aturan rantai didapat

, v d dv dt d d dv dt dv θ θ θ = =

Sehingga persamaan (2.2) dapat ditulis

) , ( v f d dv v θ θ =

2.3 Persamaan Diferensial Pendulum

Gerak dari ayunan pendulum memiliki suatu daya tarik hipnotik yang sangat kuat terhadapnya. Galileo, Newton, Bernoulli dan ilmuwan Belanda Christian Huygens (1629-1695) semuanya mengamati gerakan pendulum, memikirkan secara mendalam tentang apa yang mereka lihat dan menciptakan model matematika untuk gerakannya.

Pendulum adalah salah satu permasalahan fisika yang merupakan suatu benda yang tergantung pada seutas tali yang tidak molor, sehingga dapat bergerak dengan bebas dalam bidang vertikal.

Beberapa asumsi dasar tentang pendulum dalam hukum fisika agar didapat persamaan pendulum yaitu :

1. Gaya yang bekerja pada pendulum hanya gravitasi.

2. Tali tidak molor, dengan panjang konstan dan tanpa massa.

3. Pendulum berayun tanpa gesekan dan medium terpusat pada satu titik.

4. Massa pendulum adalah massa suatu partikel.

Untuk menerapkan hukum fisika mempunyai besaran – besaran yang mempengaruhi kerja pendulum yaitu :

1. Massa pendulum m. 2. Panjang Tali L.

3. Percepatan gravitasi g. 4. Waktu t.

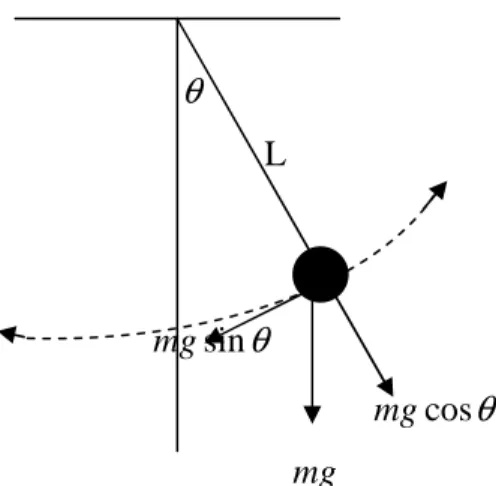
Gambar 2.1 memperlihatkan sebuah pendulum yang panjangnya L dengan massa partikel m, membentuk sudut θ dengan bidang vertikal. Gaya yang bekerja pada m adalah mg yaitu gaya gravitasi.

θ L

mgsinθ

mgcosθ

mg

Gambar 2.1 Gaya gravitasi pendulum sederhana

Jika pendulum dilepas dari keadaan diam, maka pendulum akan berayun dan bergerak membentuk busur lingkaran. Berdasarkan hukum Newton II ; gaya – gaya yang bekerja pada pendulum,

θ sin

mg F =−

oleh karena F =ma, maka θ sin mg ma=− a=−gsinθ dengan θ l s= dt d l dt ds v= = θ 2 2 2 2 dt d l dt s d a= =

θ

sehingga

θ

θ

sin 2 2 g dt d l =−

0 sin 2 2 = +

θ

θ

l g dt d (2.3)

oleh karena itu, persamaan (2.3) dapat dinyatakan sebagai persamaan pendulum yaitu 0 sin "+ θ = θ l g (2.4)

berdasarkan syarat awal

0 ) 0 ( θ θ t = = dan θ'(t =0)=0 dengan θ adalah simpangan,

g adalah percepatan gravitasi, L adalah panjang tali,

t adalah waktu.

2.4 Metode Dekomposisi Adomian

Metode dekomposisi Adomian adalah salah satu metode yang digunakan untuk menyelesaikan persamaan diferensial nonlinear berdasarkan nilai awalnya.

) (t N R Lθ + θ + θ =φ θ θ φ θ t R N L = ( )− −

θ

θ

φ

θ

L t L R L N L L_tt−1 = _tt−1 ( )− −_tt1 − _tt−1 (2.5) dimana _n n dt d

L= adalah operator diferensial. Diasumsikan bahwa invers operator L ada, dan merupakan integral sebanyak orde yang ada pada L terhadap −_tt1

t dari 0 sampai t. Ambil n=2, maka ₂

2 dt d L= sehingga :

∫ ∫

⋅ = ⋅ − t t tt dtdt L 0 0 1 ) ( ) (

dari persamaan (2.5) diperoleh :

θ θ φ θ θ θ(t)= (0)+t '(0)+L_tt−1 (t)−L_tt−1R −L_tt−1N (2.6) diasumsikan bahwa Nθ adalah deret polinomial Adomian A_n, ditulis

∑

∞ = = 0 n n A Nθ Misalkan Nθ = f(θ), maka

∑

∞ = = 0 1 0, , , ) ( ) ( n n n A f θ θ θ L θ

oleh karena deret polinomial Adomian A_i(i=0,1,L,n) _{bergantung kepada} n

θ

θ

θ

θ

0, 1, 2,L, dan merupakan deret konvergen, sehingga ) ( ₀ 0 f

θ

A = maka       = ( ₀) 0 1 1

θ

θ

θ

f d d A               +       = ( ) ! 2 ) ( _{2 0} 0 2 2 1 0 0 2 2

θ

θ

θ

θ

θ

θ

f d d f d d A             +       +       = ( ) ! 3 ) ( ) ( _{3 0} 0 3 3 1 0 2 0 2 2 1 0 0 3 3

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

f d d f d d f d d A       +             + +       = ! 2 ) ( ! 2 ) ( 2 2 1 0 2 0 2 3 1 2 2 0 0 4 4

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

f d d f d d A M             +       ) ( ! 4 ) ( _{4 0} 0 4 4 1 0 3 0 3

θ

θ

θ

θ

θ

d f d f d d

sehingga f(

θ

) dapat disusun kembali sebagai deret,

∑

∞ = = 0 1 0, , , ) ( ) ( n n n A f

θ

θ

θ

L

θ

∑

∞ =                     ₋ = 0 0 0 0 ) ( ! ) ( n n n n f d d n

θ

θ

θ

θ

Contoh 2.1

Misalkan Nθ =θ3, carilah nilai A sampai ₀ A ₅

Penyelesaian : 3 0 0 =θ A 1 2 0 1 =3θ θ A 2 1 0 2 2 0 2 =3θ θ +3θ θ A 2 1 0 3 2 0 3 1 3 =θ +3θ θ +6θ θθ A 3 1 0 0 2 2 2 2 1 4 2 0 4 =3θ θ +3θ θ +3θ θ +6θ θ θ A 3 2 0 4 1 0 1 2 2 3 2 1 5 2 0 5 =3θ θ +3θ θ +3θ θ +6θ θθ +6θ θ θ A _■ Contoh 2.2

Misalkan Nθ =sinθ, carilah nilai A sampai ₀ A ₃

Penyelesaian : 0 0 =sin

θ

A 0 1 1 =

θ

cos

θ

A 0 2 0 2 1 2 =−(

θ

/2)sin

θ

+

θ

cos

θ

A 0 3 0 2 1 0 3 1

3 =−(

θ

/6)cos

θ

−

θ

θ

sin

θ

+

θ

cos

θ

A _■

Pembahasan sebelumnya, polinomial Adomian A digunakan untuk n menghampiri bentuk nonlinier tunggal, pada kasus bentuk nonlinier yang melibatkan derivatifnya, ) ( ) ( ) (

θ

g

θ

h

θ

f =

maka polinomial Adomian An, adalah

0 1 1 2 2 1 1 0C BC B C B C B C B A_n = _n+ _n− + _n− +L+ _n− + _n

Bentuk B_i(i=0,1,2,L,n) _{diperoleh dari pengertian polinomial Adomian} sebelumnya untuk g(

θ

), yaitu

) ( ₀

0 g

θ

      = ( ₀) 0 1 1

θ

θ

g

θ

d d B               +       = ( ) ! 2 ) ( 2 0 0 2 2 1 0 0 2 2

θ

θ

θ

θ

θ

θ

g d d g d d B             +       +       = ( ) ! 3 ) ( ) ( 3 0 0 3 3 1 0 2 0 2 2 1 0 0 3 3

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

f d d f d d f d d B       +             + +       = ! 2 ) ( ! 2 ) ( 2 2 1 0 2 0 2 3 1 2 2 0 0 4 4

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

f d d f d d B M             +       ) ( ! 4 ) ( 4 0 0 4 4 1 0 3 0 3

θ

θ

θ

θ

θ

d f d f d d

dan Ci(i=0,1,2,L,n) diperoleh dengan cara yang sama, yaitu ) ( ₀ 0 h

θ

C =       = ( ₀) 0 1 1

θ

θ

f

θ

d d C               +       = ( ) ! 2 ) ( _{2 0} 0 2 2 1 0 0 2 2

θ

θ

θ

θ

θ

θ

f d d f d d C             +       +       = ( ) ! 3 ) ( ) ( _{3 0} 0 3 3 1 0 2 0 2 2 1 0 0 3 3

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

f d d f d d f d d C       +             + +       = ! 2 ) ( ! 2 ) ( 2 2 1 0 2 0 2 3 1 2 2 0 0 4 4

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

f d d f d d C M             +       ) ( ! 4 ) ( _{4 0} 0 4 4 1 0 3 0 3

θ

θ

θ

θ

θ

d f d f d d

∑

= − − − − = + + + + + = + + + + = + + + = + + = + = = n i n i n n n n n n C B C B C B C B C B C B A C B C B C B C B C B A C B C B C B C B A C B C B C B A C B C B A C B A 0 1 0 1 1 2 2 1 1 0 0 4 1 3 2 2 3 1 4 0 4 0 3 1 2 2 1 3 0 3 0 2 1 1 2 0 2 0 1 1 0 1 0 0 0 L M

Menurut (G. Adomian) metode dekomposisi memuat komposisi fungsi-fungsi tak diketahui yaitu fungsi-fungsi θ(t). Fungsi θ(t)adalah jumlah komponen – komponen yang didefinisikan sebagai deret dekomposisi yaitu deret dari

, ), ( ), ( ), (t

θ

1 t

θ

2 t L

θ

yang ditulis L + + + = ( ) ( ) ( ) ) (t

θ

0 t

θ

1 t

θ

2 t

θ

∑

∞ = = 0 ) ( n n t θ (2.7)

selanjutnya, subtitusi persamaan (2.7) ke persamaan (2.6) dapat diurai menjadi :

∑

∞

∑

= ∞ = − − ₋ − = 0 0 1 1 0( ) ( ) ) ( n n n tt n ttR t L A L t t θ θ θ dengan 0 1 0 1 1(t) Ltt R Ltt A − − ₋ − = θ θ 1 1 1 1 2(t) Ltt R Ltt A − − ₋ − = θ θ 2 1 2 1 3(t) Ltt R Ltt A − − ₋ − = θ θ n tt n tt n t L R L A 1 1 1( ) − − + =− θ − θ M

Selanjutnya setelah nilai suku – suku θ0(t),θ1(t),θ2(t),L,θn+1(t) telah diketahui, maka penyelesaian dapat diperoleh

∑

− = = 1 0 ) ( n k k t θ θ

2.5 Metode Pertubasi Homotopi

Metode pertubasi homotopi adalah salah satu metode yang digunakan untuk menyelesaikan persamaan diferensial nonlinier dan metode pertubasi homotopi ini mempunyai tujuan utama untuk mengecilkan atau menyelesaikan suatu masalah yang sulit ke suatu masalah yang mudah untuk diselesaikan.

Diberikan persamaan diferensial nonlinear :

( ) ( )

v − f r =0

A ,r∈Ω (2.8) dengan kondisi batas:

0 , =      dt dv v B ,r∈Γ dengan A adalah operator diferensial umum, B adalah batas operator terbatas,

( )

r

f adalah analisis fungsi yang diketahui dan fungsi Γ adalah batas dari domain

Ω.

Misalkan A terdiri dari dua bagian yaitu L dan N, dengan L adalah linier dan N adalah nonlinier, sehingga A

( ) ( ) ( )

v =L v +N v . Oleh karena itu, persamaan (2.8) dapat ditulis kembali sebagai berikut

0 ) ( ) ( ) (v +N v − f r = L ,r∈Ω (2.9) jika diasumsikan invers operator L_tt−1 ada, dan merupakan intergral sebanyak orde yang ada pada L terhadap t dari 0 sampai t . Ambil n=2, maka

2 2 dt d L sehingga :

( )

⋅ =

_{∫ ∫}

( )

⋅ − t t tt dtdt L 0 0 1

selanjutnya akan dibangun sebuah homotopi θ(r,p):Ω×[0,1]→ℜ yang memenuhi :

[

( ) ( )

] [

( ) ( )

]

0 ) 1 ( ) , (v p = − p L v −L 0 + p A v − f r = H

θ

,p∈[0,1]. (2.10) atau

[

( ) ( )

]

0 ) ( ) ( ) ( ) , (v p = L v −L 0 + pL 0 + p N v − f r = H

θ

θ

(2.11)

jika p=0 dan p=1 maka persamaan (2.11) menjadi

( ) ( ) ( )

v,0 =Lv −L

θ

0 =0

H (2.12)

( ) ( ) ( )

v,1 = A v − f r =0

H (2.13) dengan persamaan (2.12) dan persamaan (2.13) disebut homotopi, untuk p=0 persamaan (2.12) adalah persamaan linier, dan untuk p=1, persamaan (2.13) adalah persamaan nonlinier. Oleh karena p∈[0,1] merupakan parameter kecil yang digunakan.

Oleh karena bentuk homotopi digunakan pada persamaan nonlinear,maka solusi dari persamaan (2.11)

L + + + = ( ) ( ) 2( ) 2 1 0 t pv t p v t v v (2.14) parameter kecil p→1, sehingga

L + + + = = →1 0 1 2 limv v v v p

θ

(2.15) Menurut HPM, mengubah atau membangun sebuah homotopi sebagai berikut : 0 )] ( ) ( ) ( [ ) ( ) ( ) , (v p = L v −L 0 + p L 0 +N v − f r = H

θ

θ

(2.16)

dengan p∈[0,1] yang merupakan parameter penempel dan

θ

₀ adalah nilai awal yang secara umum memenuhi syarat batas yang diberikan

) ( ) ( [ ) ( ) ( 0 0 0 1 2 2 2 2 1 0 +v p+v p +L −L + p L +N v +v p+v p +L v L θ θ 0 )] ( = − f r (2.17)

untuk orde 0, _p= _p2 = _p3 =L=0_{, sehingga persamaan (2.17) menjadi} ) ( ) (v₀ Lθ₀ L = c t t v0( )=θ(0)=θ0( )=

untuk orde 1, p≠0, _p2 = _p3 =L=0_{, sehingga persamaan (2.17) menjadi} 0 ) 0 ( , 0 ) ( ) ( ) ( ) (v₁ +L ₀ +N v₀ − f r = v₁ = L θ ) ( ) ( ) ( ) ( 1 ₀ 1 ₀ 1 t L L N v f r v =− _tt− θ − _tt− +

0 ) 0 ( , 0 ) ( ) (v2 +N v1 = v2 = L ) ( ) ( 1 ₁ 2 t L N v v =− _tt−

untuk orde 3, p3 ≠0, _p= _p2 =L=0_{, sehingga persamaan (2.17) menjadi} 0 ) 0 ( , 0 ) ( ) (v3 +N v2 = v3 = L ) ( ) ( 2 1 3 t L N v v tt − − =

Selanjutnya setelah nilai suku – suku diketahui, maka penyelesaian dapat diperoleh dengan menggunakan hampiran

∑

− = → = = 1 0 1 ( ) lim ) ( n k k p v v t t θ 2.6 Maple

Maple sering digunakan untuk keperluan penyelesaian permasalahan

persamaan diferensial dan visualisasinya, karena selain mudah digunakan Maple mempunyai kemampuan menyederhanakan persamaan diferensial sehingga solusi persamaan diferensial dapat dipahami dengan baik. Keunggulan dari Maple untuk aplikasi persamaan diferensial adalah kemampuan melakukan animasi (gerakan) grafik dari suatu fenomena gerakan yang dimodelkan ke dalam persamaan diferensial yang mempunyai nilai awal dan syarat batas.

Statement yang sering digunakan untuk keperluan menyelesaikan

permasalahan persamaan diferensial antara lain : diferensial digunakan untuk mendiferensialkan (menurunkan) suatu fungsi, dsolve digunakan untuk menyelesaikan persamaan diferensial, evalf memberikan nilai numeric dari suatu persamaan, dan simplify digunakan untuk menyederhanakan suatu persamaan. Namun tentu saja pernyataan – pernyataan awal seperti restart dan deklarasi

variable atau konstanta yang diperlukan tidak boleh diabaikan. Sedangkan untuk

membuat grafik digunakan perintah plot, plot 2d, plot 3d, tergantung dimensi dari pernyataan yang dimiliki, untuk membuat animasi digunakan perintah animate 3d. Setiap perintah pada Maple harus dituliskan setelah tanda Maple prompt yang diakhiri dengan titik dua (bila hasilnya tidak akan ditampilkan) atau titik koma (bila hasilnya akan ditampilkan).

Maple merupakan salah satu perangkat lunak (software) yang

dikembangkan oleh waterloo.inc. untuk keperluan computer algebraic system (CAS). Menu – menu yang terdapat pada Maple terdiri dari menu : file, edit, view, insert, format, spreadsheet, option, window, dan help merupakan menu standar yang dikembangkan untuk program aplikasi pada sistem windows.

Bahasa yang digunakan pada Maple merupakan bahasa pemrograman yang sekaligus bahasa aplikasi, sebab pernyataan atau statement yang merupakan masukan (input) pada Maple merupakan deklarasi pada bahasa program dan perintah (command) yang sering digunakan pada bahasa aplikasi.

Maple bisa dipakai untuk menganalisis dan menginterpretasikan solusi

yang diperoleh ke masalah nyata yang telah dimodelkan. Maple sangat dibutuhkan untuk membantu mempermudah menyelesaikan persamaan diferensial.

BAB III

METODOLOGI PENELITIAN

Metode yang digunakan pada skripsi ini adalah studi pustaka, dengan langkah – langkah sebagai berikut :

a) Berdasarkan metode dekomposisi Adomian

1. Menentukan persamaan diferensial pendulum nonlinear

0 sin 2 2 = +

θ

θ

l g dt d

, berdasarkan nilai awal

θ

(0)=c₁ dan

θ

'(0)=c₂. 2. Menentukan bentuk operator diferensial θ sinθ

l g

L =− .

3. Menentukan bentuk invers operator 1θ 1 sinθ

l g L Ltt tt − − ₌₋ .

4. Menentukan nilai polinomial nonlinear Adomian untuk N(θ)=sinθ ,

sehingga

∑

∞ = = 1 ) ( i i A N θ . 5. Menentukan nilai θ₀,θ₁,θ₂,K,θ_n+1. 6. Menentukan θ(t)=θ0 +θ1 +θ2 +L+θn+1.

b) Berdasarkan metode pertubasi homotopi

1. Menentukan persamaan diferensial pendulum nonlinear

0 sin 2 2 = + θ θ l g dt d

, berdasarkan nilai awal

θ

(0)=c1 dan 2 ' ) 0 ( =c θ . 2. Mengekspansi nilai ! 5 ! 3 sin 5 3 θ θ θ θ ≈ − + .

3. Mensubtitusikan persamaan (2.14) ke persamaan (4.14). 4. Menyusunkannya berdasarkan orde pertubasi p.

5. Menentukan nilai v₀,v₁,v₂,K,v_n+1.

BAB IV

PEMBAHASAN

Bab ini membahas tentang penyelesaian persamaan pendulum dengan menggunakan metode dekomposisi Adomian dan metode pertubasi homotopi.

4.1 Penyelesaian dengan Metode Dekomposisi Adomian

Pertimbangkan kembali persamaan pendulum nonlinear berikut

0 ) ( 2 2 = +

ω

θ

θ

f dt d (4.1)

dengan ω =g /l dan f(θ)=sinθ berdasarkan nilai awal

θ

(0)=c1 dan 2

) 0 (

' =c

θ

sehingga persamaan (4.1) menjadi ) ( 2 2 θ ω θ f dt d − = (4.2)

persamaan (4.2) dapat ditulis dalam bentuk operator θ

θ t N

L ( )=− (4.3)

untuk menyelesaikan Lθ(t) pada persamaan (4.3) maka diterapkan invers operator ke dalam persamaan (4.3) sehingga diperoleh

θ

θ t L N

L

L_tt−1 ( )=− −_tt1 (4.4)

berdasarkan nilai awal

θ

(0)=c₁ dan

θ

'(0)=c₂ maka persamaan (4.4) dapat ditulis θ θ θ θ t t Ltt N 1 ) 0 ( ' ) 0 ( ) ( = + − − atau θ θ t c tc Ltt N 1 2 1 ) ( = + − − (4.5)

Penyelesaian pada persamaan (4.5) merupakan komposisi fungsi – fungsi tak diketahui yaitu fungsi θ(t) yang merupakan deret θ₀(_t),θ₁(_t),θ₂(_t),L, _ditulis

L + + + = ( ) ( ) ( ) ) (t θ₀ t θ₁ t θ₂ t θ

∑

∞ = = 0 ) ( n n t θ

Selanjutnya komponen nonlinear Nθ diekspansi dengan menggunakan deret polinomial Adomian A ditulis _n,

∑

∞ = = 0 n n A Nθ

maka persamaan (4.5) menjadi

      − + =

∑

∞ = − 0 1 2 1 ) ( n n tt A L tc c t

θ

atau

[

+ + +L

]

− + = − − − 2 1 1 1 0 1 2 1 ) (t c tc L_tt A L_tt A L_tt A θ (4.6)

polinomial Adomian A pada persamaan (4.6) diperoleh dari _n

0 0 =sinθ A (4.7) 0 1 1 =θ cosθ A (4.8) 0 2 0 2 1 2 =−(θ /2)sinθ +θ cosθ A (4.9) M oleh karena, 1 0 =c θ maka 0 1 1 Ltt A − − = θ =−L−_tt1ωsinθ₀ =−(sinθ0)ωt2/2! 1 1 2 Ltt A − − = θ 1 ₀ cosθ ω − − = Ltt =(ω2t4 /4!)sinθ₀cosθ₀ 2 1 3 Ltt A − − = θ

Selanjutnya setelah nilai suku – suku _{( ), ( ), ( ),}K 2 1 0 t

θ

t

θ

t

θ

diketahui, maka penyelesaian diperoleh

∑

∞ = = 0 ) ( ) ( n n t t θ θ Contoh 4.1

Tentukan penyelesaian dari persamaan diferensial pendulum nonlinear berikut 0 sin 2 2 = + θ θ l g dt d (4.10)

dengan masalah nilai awalnya θ(0)=1 dan θ'(0)=0 dengan =10

l g

.

Penyelesaian :

Penyelesaian persamaan diferensial pendulum nonlinear pada persamaan (4.10) dilakukan dengan menentukan θ0, yang ditulis

) ( ) 0 ( ) 0 ( ) ( ' 1 0 t θ tθ Lttφ t θ _{= + +} −

Berdasarkan nilai awal θ(0)=1 dan θ'(0)=0, maka 1

) (

0 t =

θ

Untuk memperoleh nilai

θ

₁(t), maka terlebih dahulu ditentukan A 0

berdasarkan persamaan (4.7) dan diperoleh 8414709848 , 0 ) 1 sin( ) sin( ₀ 0 = θ = = A Oleh karena, ) ( ) ( 0 1 1 t Ltt A − − = θ maka

∫ ∫

− = t t dtdt t 0 0 0 1( ) (

ω

sin

θ

)

θ

=−4,207354924t2

Selanjutnya nilai A1 diperoleh dengan menggunakan persamaan (4.8), yaitu 2 2 0 1 1 273243567 , 2 ) 1 cos( 207354924 , 4 cos t t A − = − = =

θ

θ

maka ) ( ) ( 1 1 2 t Ltt A − − = θ 4 0 0 0 1 2 894369639 , 1 ) cos ( t dtdt t t = − − =

_{∫ ∫}

ω

θ

θ

Selanjutnya nilai A₂ diperoleh dengan menggunakan persamaan (4.9), yaitu ) 1 cos( ) 1 sin( ) 2 / ( 2 2 1 2 =−

θ

+

θ

A =−6,424258176t4 maka ) ( ) ( 1 ₂ 3 t Ltt A − − =

θ

=−

∫ ∫

− − t t dtdt 0 0 0 3 0 2 0 3 ) sin 3 cos sin (

ω

θ

θ

θ

=2,141419392t6

Selanjutnya nilai A diperoleh dengan menggunakan persamaan (4.9), 3

yaitu ) 1 cos( ) 1 sin( ) 1 cos( ) 6 / ( ₁3 _{1 2 3} 3 =−

θ

−

θ

θ

+

θ

A =12,25651402t6 maka ) ( ) ( 3 1 4 t Ltt A − − =

θ

=−

∫ ∫

− + t t dtdt 0 0 0 3 0 0 0 3 4 ) cos sin cos sin 33 (

θ

θ

θ

θ

ω

=−2,601882448t8

Penyelesaian persamaan (4.10) dapat diperoleh dengan cara menjumlahkan suku – suku _{( ), ( ), ( ), ( ),}K

3 2 1 0 t

θ

t

θ

t

θ

t

θ

atau ditulis L + + + + + = ( ) ( ) ( ) ( ) ( ) ) (t

θ

₀ t

θ

₁ t

θ

₂ t

θ

₃ t

θ

₄ t

θ

L + − + + − = 8 6 4 2 601882448 , 2 141419392 , 2 894369639 , 1 207354924 , 4 1 t t t t ■

Gambar 4.1 di bawah ini menunjukkan bahwa akurasi penyelesaian θ(t) yang diperoleh dengan menggunakan metode dekomoposisi Adomian untuk empat suku terhadap penyelesaian eksak persamaan diferensial pendulum nonlinear.

Gambar 4.1 Penyelesaian persamaan (4.10) berdasarkan

nilai awal θ(0)=1 dan θ'(0)=0 dengan =10

l g

.

Gambar 4.4 diatas untuk persamaan pendulum nonlinear, sedangkan untuk membandingkan dengan pendulum linear menggunakan metode pertubasi homotopi dapat dilihat pada contoh 4.2 berikut.

Contoh 4.2

Tentukan penyelesaian dari persamaan diferensial pendulum linear berikut

0 2 2 = + θ θ l g dt d (4.11)

dengan masalah nilai awal θ(0)=1 dan

θ

'(0)=3, dengan =−4

l g

.

Solusi eksak adalah t e2t e 2t

4 1 4 5 ) ( = − − θ Penyelesaian :

Penyelesaian persamaan diferensial pendulum linear pada persamaan

(4.11) dilakukan dengan menentukan θ0, yang ditulis

) ( ) 0 ( ) 0 ( ) ( ' 1 0 t θ tθ Lttφ t θ _{= + +} −

Berdasarkan nilai awal θ(0)=1 dan θ'(0)=3, maka

t t) 1 3 ( 0 = + θ maka

∫ ∫

+ = t t dtdt t t 0 0 1( ) 4 (1 3)

θ

=2t2 +2t3 dan

∫ ∫

+ = t t t t dtdt t 0 0 3 2 2( ) 4 (2 2 )

θ

5 4 5 2 3 2 t t + = maka

∫ ∫

+ = t t dtdt t t t 0 0 5 4 3 ) 5 2 3 2 ( 4 ) (

θ

7 6 105 4 45 4 t t + = dan

∫ ∫

+ = t t dtdt t t t 0 0 7 6 4 ) 105 4 45 4 ( 4 ) (

θ

9 8 945 2 315 2 t t + =

Penyelesaian persamaan (4.11) dapat diperoleh dengan cara menjumlahkan suku – suku _{( ), ( ), ( ), ( ),}K

3 2 1 0 t

θ

t

θ

t

θ

t

θ

atau ditulis L + + + + + = 0( ) 1( ) 2( ) 3( ) 4 ) (

θ

θ

θ

θ

θ

θ

t t t t t = + + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +L 945 2 315 2 105 4 45 4 5 2 3 2 2 2 3 1 t t t t t t t t t _■

Akurasi penyelesaian θ(t) bergantung kepada banyaknya suku – suku yang dijumlahkan.

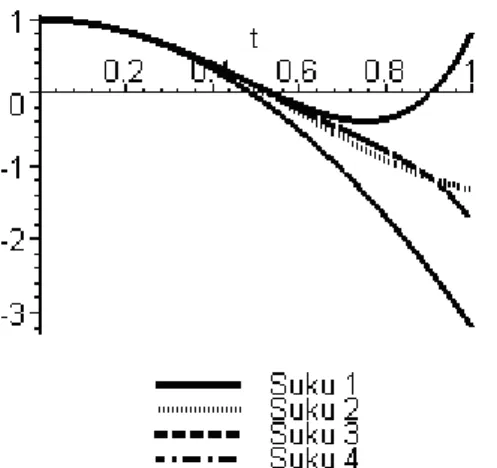
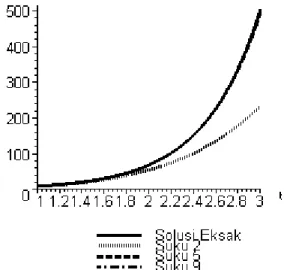
Gambar 4.2 di bawah ini menunjukkan bahwa akurasi penyelesaian θ(t) yang diperoleh dengan menggunakan metode dekomoposisi Adomian untuk beberapa suku terhadap penyelesaian eksak persamaan diferensial pendulum linear.

Gambar 4.2 Penyelesaian persamaan (4.11) berdasarkan nilai awal θ(0)=1 dan θ'(0)=3 dengan =−4

l g

.

Berdasarkan gambar 4.2 dapat dilihat bahwa, kurva yang dibentuk oleh )

(

9 t

θ lebih mendekati dibandingkan kurva – kurva lainnya. Hal ini menunjukkan suku lebih banyak akan mendekati kurva penyelesaian eksaknya. Sedangkan untuk memperkecil error yang dihasilkan oleh beberapa kurva terhadap solusi eksak, dilihat pada gambar 4.3

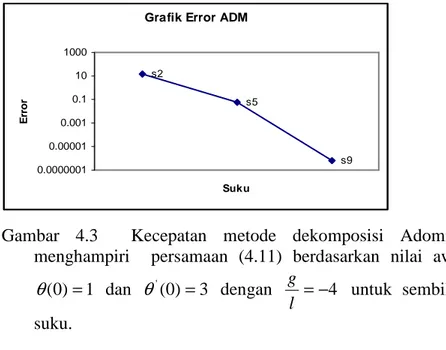
Grafik Error ADM s2 s5 s9 0.0000001 0.00001 0.001 0.1 10 1000 Suku E rr o r

Gambar 4.3 Kecepatan metode dekomposisi Adomian menghampiri persamaan (4.11) berdasarkan nilai awal

1 ) 0 ( = θ dan

θ

'(0)=3 dengan =−4 l g untuk sembilan suku.

4.2 Penyelesaian dengan Metode Pertubasi Homotopi

Pertimbangkan kembali persamaan pendulum nonlinear berikut :

0 ) ( 2 2 = +

ω

θ

θ

f dt d (4.12)

dengan

ω

= g/l dan f(

θ

)=sin

θ

nilai awal

θ

(0)=c1 dan 2 ' ) 0 ( =c

θ

, sehingga persamaan (4.12) menjadi

θ

θ

sin 2 2 l g dt d ₌₋ (4.13)

persamaan (4.13) dapat ditulis dalam bentuk homotopi dengan

! 5 ! 3 sin 5 3

θ

θ

θ

θ

≈ − + berikut 0 ] ! 3 ) ( [ ) ( ) ( 3 0 0  =      − − + −L p L v v v L

θ

θ

ω

(4.14)

Subtitusi persamaan (2.14) ke persamaan (4.14) sehingga penyelesaian dari persamaan (4.14) disusun berdasarkan orde pertubasi p berikut

− + + + + − + + + ) ( ) [ ( ) (_{v0 v1p v2p}2 L _{L 0 p v0 v1p v2p}2 L L θ ω

ω

] 0 ! 3 ) ( _{0 1 2} 2 3 = + + +_{v p v p} L v (4.15)

untuk orde nol, _p= _p2 = _p3L=0 0 ) ( ) (v₀ −L

θ

₀ = L 0 0 =

θ

v (4.16)

untuk orde satu, p≠0, _p2 = _p3L=0

0 ! 3 ) ( 3 0 0 1 =      − + v v v L

ω

      + − = − ! 3 3 0 0 1 1 v v L v tt

ω

(4.17)

untuk orde dua, p2 ≠0, _p= _p3 = _p4K=0 0 2 1 ) ( _{2 1 0}2 ₁=      ₋ + v v v v L ω       + − = − 1 2 0 1 1 2 2 1 v v v L v ttω (4.18)

untuk orde tiga, 3 ≠0

p , = 2 = 4 = 5_L=0 p p p p 0 2 1 2 1 ) ( _{3 2 0}2 _{2 0 1}2=      − − + v v v v v v L ω       + + − = − 2 1 0 2 2 0 2 1 3 2 1 2 1 v v v v v L v ttω (4.19)

untuk orde empat, p4 ≠0, _p= _p2 = _p3 = _p5 = _p6L=0 0 6 1 ) ( _{4 3 0 1 2 1}3=      − − + v v vv v v L ω       + + − = − 3 1 2 1 0 3 1 4 6 1 v v v v v L v ttω (4.20)

Selanjutnya setelah nilai suku-suku v₀(t),v₁(t),v₂(t),K,v_{n+1 diketahui,}

maka penyelesaian dapat diperoleh dengan menggunakan hampiran v t p 1 lim ) ( → =

θ

dengan

∑

− = = 1 0 ) ( n k k t v v

Contoh 4.1

Tentukan penyelesaian dari persamaan diferensial pendulum nonlinear berikut 0 sin 2 2 = +

θ

θ

l g dt d (4.21)

dengan masalah nilai awalnya θ(0)=1 dan θ'(0)=0 dengan =10

l g

.

Penyelesaian :

Penyelesaian persamaan diferensial pendulum nonlinear pada persamaan (4.21) dilakukan dengan menentukan v , yang diperoleh dari persamaan (4.16) 0

1

0 0 =θ =

v

untuk orde 1, p≠0, _p2 = _p3 =L=0_{, sehingga persamaan (4.17)}       + − = − ! 3 10 3 0 0 1 1 v v L v tt 2 6 25 t − = untuk orde 2, 2 ≠0 p , = 3 =_L=0 p p , sehingga persamaan (4.18)       + − = − 1 2 0 1 1 2 2 1 10 v v v L v _tt 4 72 125 t =

untuk orde 3, p3 ≠0, _p= _p2 = _p4 =L=0_{, sehingga persamaan (4.19)}

     _{− + +} = − 2 1 0 2 2 0 2 1 3 2 1 2 1 10 v v v v v L v tt 6 48 125 t =

untuk orde 4, p4 ≠0, _p= _p2 = _p3 = _p5 =L=0_{sehingga persamaan (4.20)}

      + + − = − 3 1 2 1 0 3 1 4 6 1 10 v v v v v L v tt 8 36288 141875 t − =

Penyelesaian persamaan (4.21) dapat diperoleh dengan cara menjumlahkan suku – suku v0(t),v1(t),v2(t),K,vn+1 atau ditulis

L + + + + + = ( ) ( ) ( ) ( ) ( ) ) (t v₀ t v₁ t v₂ t v₃ t v₄ t

θ

= − 2 + 4 + 6 − 8 +L 36288 141875 48 125 72 125 6 25 1 t t t t _■

Gambar 4.4 di bawah ini menunjukkan bahwa akurasi penyelesaian θ(t) yang diperoleh dengan menggunakan metode pertubasi homotopi untuk empat suku terhadap penyelesaian eksak persamaan diferensial pendulum nonlinear.

Gambar 4.4 Penyelesaian persamaan (4.21) berdasarkan nilai awal θ(0)=1 dan θ'(0)=0 dengan

10

=

l g

.

Gambar 4.4 diatas untuk persamaan pendulum nonlinear, sedangkan untuk membandingkan dengan pendulum linear menggunakan metode pertubasi homotopi dapat dilihat pada contoh 4.2 berikut.

Contoh 4.2

Tentukan penyelesaian dari persamaan diferensial pendulum linear berikut

0 2 2 = + θ θ l g dt d (4.22)

dengan masalah nilai awal θ(0)=1 dan θ'(0)=3, dengan =−4

l g

Solusi eksak adalah e2t e 2t 4 1 4 5 _{− −} Penyelesaian :

Jika menggunakan metode pertubasi homotopi maka harus menentukan nilai _{( ), ( ), ( ), ( ),}K 3 2 1 0 t v t v t v t v yaitu 0 ) ( ) ( ) ( 0  =      + − v l g p L v L θ 0 ) ( ) ( ) ( 0 0 1 2 2 2 2 1 0 =      + + + + − + + + L _{v v p v p} L l g p L p v p v v L θ (4.23)

untuk orde 0, _p= _p1 = _p2L=0_{, sehingga persamaan (4.23)} 0 ) ( ) (v0 −L

θ

0 = L t v0 =

θ

0 =1+3

untuk orde 1, p≠0, _p2 = _p3 =L=0_{, sehingga persamaan (4.23)} 0 ) ( ) ( 1 0 =      + v l g v L

∫ ∫

+ = t t dtdt t v 0 0 1 4 (1 3 ) 3 2 1 2t 2t v = +

untuk orde 2, p2 ≠0, _p= _p3 =L=0_{, sehingga persamaan (4.23)} 0 ) ( ) (( 2 1 =      + v l g v L

∫ ∫

+ = t t t t dtdt v 0 0 3 2 2 4 (2 2 ) 5 4 2 5 2 3 2 t t v = +

untuk orde 3, p3 ≠0, _p= _p2 = _p4 =L=0_{, sehingga persamaan (4.23)} 0 ) ( ) ( 3 2 =      + v l g v L

∫ ∫

+ = t t dtdt t t v 0 0 5 4 3 ) 5 2 3 2 ( 4 7 6 3 105 4 45 4 t t v = + untuk orde 4, 4 ≠0 p , = 2 = 3 =_L=0 p p p , sehingga persamaan (4.23) 0 ) ( ) ( _{4 3} =      + v l g v L

∫ ∫

+ = t t dtdt t t v 0 0 7 6 4 ) 105 4 45 4 ( 4 9 8 4 945 2 315 2 t t v = +

Penyelesaian persamaan (4.22) dapat diperoleh dengan cara menjumlahkan suku – suku v₀(t),v₁(t),v₂(t),K,v_{n+1 atau ditulis}

L ) ( ) ( ) ( ) ( ) ( ) (t =v₀ t +v₁ t +v₂ t +v₃ t +v₄ t

θ

= + + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +L 945 2 315 2 105 4 45 4 5 2 3 2 2 2 3 1 t t t t t t t t t _■

Akurasi penyelesaian θ(t) bergantung kepada banyaknya suku – suku yang dijumlahkan.

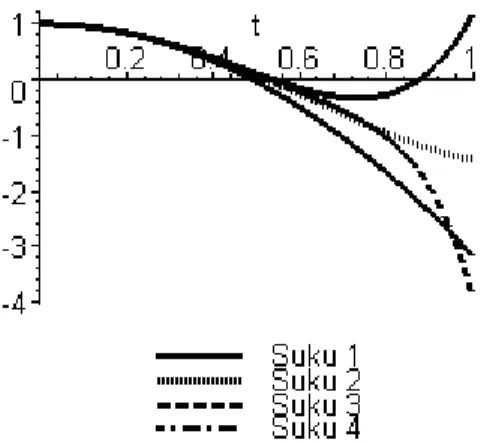
Gambar 4.5 di bawah ini menunjukkan bahwa akurasi penyelesaian θ(t) yang diperoleh dengan menggunakan metode pertubasi homotopi untuk beberapa suku terhadap penyelesaian eksak persamaan diferensial pendulum linear.

Gambar 4.5 Penyelesaian persamaan (4.22) berdasarkan nilai awal θ(0)=1 dan

θ

'(0)=3 dengan

4 − = l g .

Berdasarkan gambar 4.5 dapat dilihat bahwa kurva yang dibentuk oleh )

(

9 t

θ

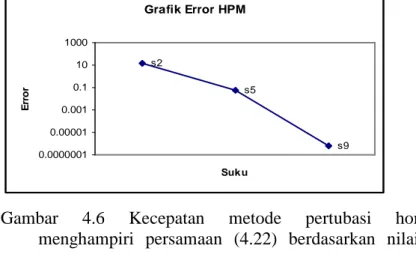
lebih mendekati dibandingkan kurva – kurva lainnya. Hal ini menunjukkan suku lebih banyak akan mendekati kurva penyelesaian eksaknya. Sedangkan untuk memperlihatkan error yang dihasilkan oleh beberapa kurva terhadap solusi

eksak, dilihat pada gambar 4.6

Grafik Error HPM s2 s5 s9 0.0000001 0.00001 0.001 0.1 10 1000 Suk u E rr o r

Gambar 4.6 Kecepatan metode pertubasi homotopi menghampiri persamaan (4.22) berdasarkan nilai awal

1 ) 0 ( =

θ

dan

θ

'(0)=3 dengan =−4 l g untuk sembilan suku.

BAB V

PENUTUP

5.1 Kesimpulan

Berdasarkan pembahasan dari skripsi ini diperoleh kesimpulan sebagai berikut

a) Metode dekomposisi Adomian menyelesaikan persamaan diferensial

pendulum nonlinear ₂ sin 0

2 = +

θ

θ

l g dt d

, berdasarkan masalah nilai awal

1 ) 0 ( =c

θ

dan

θ

'(0)=c₂ menghasilkan L + + + + = 0 0 4 0 2 2 1 sin cos ! 4 sin 2 ) ( θ θ θ θ t l g t l g tc c t

b) Metode pertubasi homotopi menyelesaikan persamaan diferensial

pendulum nonlinear ₂ sin 0

2 = + θ θ l g dt d

, berdasarkan masalah nilai awal

1 ) 0 ( =c

θ

dan

θ

'(0)=c₂ menghasilkan L +       − +       − + = ! 3 3 ! 3 ) 0 ( ) ( 1 2 0 1 3 0 0

θ

θ

θ

θ

θ

θ

θ

l g l g t 5.2 Saran

Skripisi ini membahas tentang penyelesaian persamaan diferensial

pendulum nonlinear ₂ sin 0

2 = + θ θ l g dt d

, berdasarkan masalah nilai awal

θ

(0)=c₁ dan

θ

'(0)=c₂ dengan komponen nonlinearnya Nθ =sinθ menggunakan metode dekomposisi Adomian dan metode homotopi pertubasi. Bagi pembaca yang berminat melanjutkan skripsi ini, penulis sarankan membahas tentang persamaan diferensial pendulum nonlinear dengan menggunakan metode – metode lain, atau membahas tentang persamaan diferensial yang lainnya.

DAFTAR PUSTAKA

Adomian, G., Nonlinear Stochastic System Theory and Applications to Physics, Kluwer Academic. Dordrecht. London, 1989.

Adomian, G., Solving frontier problems of physics : The Decomposition Method, Kluwer Academic. Dordrecht. London, 1994.

Belendez.A, C.Pascual, D.I.Mendez, T.Belendez, C.Neipp, Exact Solution for the Nonlinear Pendulum, Departamento de Fisica, Ingenierta de Sistemas y

Teoria de ta Senal, Universidas de Alicante, Spain, 2007.

Borrelli, Robert L., Coleman, Courtney S., Differential Equations A Modeling

Perspective, Harvey Mudd College, Canada, 1998.

MD. Sazzad Hossien Chowdhury, Solving Linear And Nonlinier Differential

Equations by Homotopy Perturbation Method, Faculty Of Sciene And

Technology University Kebangsaan Malaysia Bangi, Thesis : 2007.

Sieradski, Allan J., An Introduction to Topology and Homotopy, University of Oregon, PWS-Kent Publishing Company, Boston, 1992.