ANALISIS MODEL DINAMIKA VIRUS DALAM SEL TUBUH DAN PENGARUH RESPON IMUN CTL

(1)

ANALISIS MODEL DINAMIKA VIRUS

DALAM SEL TUBUH

DAN PENGARUH RESPON IMUN CTL

Nughthoh Arfawi Kurdhi

Jurusan Matematika FMIPA Universitas Sebelas Maret, Surakarta, 57126

arfa@uns.ac.id

ABSTRAK

Berbagai jenis virus telah menyerang manusia dan menyebabkan berbagai macam penyakit. Di dalam tubuh manusia, virus menggunakan sel sebagai media untuk berkembang biak dan mempertahankan hidup. Keberadaan virus dalam tubuh akan mengaktifkan respon imun yang diperankan oleh CTL (cytotoxic T lymphocyte). Pada paper ini akan ditunjukkan dinamika virus dan pengaruh respon imun CTL dalam mengendalikan infeksi virus. Kestabilan global titik ekuilibrium model dinamika virus tanpa dan dengan respon imun CTL diselidiki dengan menggunakan fungsi Lyapunov. Hasil penelitian menunjukkan bahwa kestabilan global titik ekuilibrium tergantung dari rasio reproduksi dasar

 

R0 . Jika

1

0

R , maka titik ekuilibrium bebas virus stabil asimtotik global, sedangkan jikaR₀ 1, maka terdapat satu titik ekuilibrium endemik yang memiliki sifat stabil asimtotik global. Pengaruh respon imun CTL terhadap infeksi virus adalah menurunkan kepadatan virus bebas dan sel terinfeksi serta meningkatkan kepadatan sel tak terinfeksi.

Keywords: Virus, respon imun, CTL, stabil asimtotik global, fungsi Lyapunov.

PENDAHULUAN

Virus adalah salah satu organisme yang sering mengganggu pertumbuhan sel di dalam tubuh manusia. Hal ini dikarenakan virus menggunakan sel pada suatu organisme sebagai media untuk bereproduksi dan mempertahankan hidup, yaitu dengan mengambil alih fungsi-fungsi yang ada pada sel. Virus memiliki struktur biologis yang sangat kecil dan untuk bereproduksi membutuhkan sel pada suatu organisme. Setiap virus mempunyai afinitas terhadap tipe sel tertentu. Sebagai contoh, virus HIV hanya menyerang sel-sel CD4+ dalam darah putih dan virus Hepatitis C hanya menginfeksi sel liver.

Tubuh manusia memiliki sistem imun yang berperan melawan patogen asing, seperti virus, yang masuk ke dalam tubuh. Dalam tubuh manusia, sistem imun diperankan oleh sel B dan sel T yang diproduksi berturut-turut oleh sumsum tulang dan thymus. Kedua sel tersebut memiliki peran masing-masing. Sel B membawa molekul-molekul antibodi pada permukaan sel yang dapat mengindentifikasi dan menghancurkan virus, sedangkan sel T mampu mengidentifikasi virus dan sel terinfeksi. Salah satu jenis sel T adalah CTL (cytotoxic T

lymphocyte), yang mampu menghancurkan sel terinfeksi. Selain itu, CTL juga dapat

mengeluarkan zat kimia yang memicu reaksi di dalam sel terinfeksi. Reaksi yang terjadi dapat mencegah agar gen virus (viral genome) tidak diekspresikan menjadi partikel-partikel virus baru. Pada saat virus tertentu pertama kali menginfeksi sel dalam tubuh, respon imun yang bekerja adalah CTL, sedangkan antibodi belum dapat diaktifkan. Hal ini dikarenakan sel B belum mengenal virus tersebut.

Dalam bukunya, Nowak dan May (2000) dan Woodarz (2007) menjelaskan bahwa untuk menganalisis penyebaran dan kontrol dari infeksi virus dapat digunakan model matematika. Wodarz mengkonstruksi beberapa model (sistem persamaan diferensial) mengenai dinamika virus dan respon imun yang dihasilkan oleh tubuh. Selain itu, Wodarz juga menentukan titik ekuilibrium dan rasio reproduksi dasar,

R

₀, dari masing-masing model. Tetapi, kestabilan titik

(2)

virus tanpa dan dengan respon imun CTL. Kurdhi dan Aryati menganalisis model dengan rata-rata produksi CTL proporsional dengan kepadatan sel terinfeksi dan CTL. Namun, model tersebut memiliki dua kelemahan, yaitu (i) respon imun CTL tidak bereaksi terhadap infeksi virus untuk nilai rasio reproduksi cukup kecil, dan (ii) kepadatan sel terinfeksi pada titik kesetimbangan untuk rasio reproduksi cukup besar tidak bergantung pada parameter laju CTL menghancurkan sel terinfeksi maupun parameter virus. Kedua kelemahan tersebut dapat dihilangkan jika rata-rata produksi CTL proposional terhadap sel terinfeksi dan tidak bergantung pada kepadatan CTL. Hal ini sesuai dengan kenyataan bahwa CTL tidak memproduksi dirinya sendiri seperti pada model mangsa-pemangsa.

Dalam paper ini ditunjukkan bagaimana dinamika virus dalam sel tubuh, serta peran respon CTL dalam melawan infeksi virus. Pertama dikonstruksi model dinamika virus tanpa respon imun, menentukan titik kesetimbangan dan

R

₀, serta menganalisis kestabilan global titik ekuilibrium model dengan menggunakan fungsi Lyapunov. Selanjutnya, dikonstruksi model dinamika virus dengan respon imun CTL dan menunjukkan pengaruh respon CTL terhadap infeksi virus melalui simulasi numerik.

BAHAN DAN METODE

Fakta-fakta mengenai morfologi dan reproduksi virus, serta bagaimana sistem imun dalam tubuh manusia bekerja diperoleh dari Wodarz (2007). Berdasarkan fakta-fakta tersebut, kemudian dibentuk beberapa asumsi yang digunakan untuk memodelkan dinamika virus dalam sel tubuh tanpa dan dengan respon imun CTL ke dalam sistem persamaan diferensial nonlinear. Kedua model tersebut dianalisa melalui beberapa tahap meliputi eksistensi titik ekuilibrium, kestabilan titik ekuilibrium, dan simulasi model. Titik ekuilibrium merupakan keadaan steady

state dari model, yaitu kepadatan populasi yang terlibat dalam model tidak mengalami

perubahan dalam jangka waktu yang lama. Wodarz (2007) menyatakan bahwa secara umum titik ekuilibrium suatu model dinamika virus dibedakan menjadi titik ekuilibrium bebas virus dan endemik. Pada titik ekulibrium bebas virus, virus bebas dan sel terinfeksi sudah tidak terdapat dalam tubuh, sedangkan pada titik ekuilibrium endemik masih terjadi infeksi virus. Definisi titik ekuilibrium diperoleh di Perko (1991). Diberikan sistem persamaan diferensial











n



n n n n x x x f x x x x f x x x x f x ,..., , ,..., , ,..., , 2 1 2 1 2 2 2 1 1 1        (1)

dengan f_i:ERn R, i1,2,...,n, dan



x₁,x₂,...,x_n



E  Rn, E himpunan terbuka.

Definisi 1 Titik xˆRn disebut titik ekuilibrium Sistem (1) jika f

 

xˆ 0.

Perilaku solusi disekitar titik ekuilibrium model dapat dilihat dengan menganalisis kestabilan dari titik ekuilibrium tersebut. Konsep kestabilan ini digunakan untuk mengetahui apakah untuk jangka waktu yang lama, populasi sel dan virus akan menuju ke titik ekuilibrium bebas virus atau endemik. Definisi umum mengenai kestabilan global suatu titik ekuilibrium mengacu pada

Verhulst (1989).

Definisi 2 Titik ekuilibrium xˆRn pada Sistem (1) dikatakan stabil asimtotik global jika untuk sebarang nilai awal x

 

t0 yang diberikan, setiap solusi Sistem (1) yaitu x

 

t dengan t menuju titik ekuilibrium xˆ .

Untuk menentukan kestabilan global suatu titik ekuilibrium,

Verhulst (1989) dan

(3)

Definisi 3 Diberikan Sistem (1) dengan E Rn dan M E. Himpunan M disebut himpunan invarian terhadap Sistem (1), jika x(t0)x₀ M maka x



x0,t 



M untuk setiap t R.

Definisi 4 Diberikan fungsi V:ERn R dan xˆE titik ekuilibrium Sistem (1). Fungsi V disebut fungsi Lyapunov jika memenuhi ketiga pernyataan berikut:

a. Fungsi V kontinu dan mempunyai turunan parsial pertama yang kontinu pada E atau

) ( 1 E C V  .

b. Titik ekuilibrium xˆ merupakan satu-satunya titik minimum fungsi V pada E. c. Fungsi V memenuhi V

 

x 0 untuk setiap xE.

Sifat kestabilan global titik ekuilibrium Sistem (1) dapat dianalisis melalui Teorema 5 dan Akibat 6 yang dapat dilihat Luenberger (1979).

Teorema 5 Diberikan Sistem (1) dengan E Rn. Jika terdapat fungsi Lyapunov V, dengan (i) Ek 



xE|V(x)k



untuk suatu k 0, merupakan himpunan terbatas,

(ii) V(x)0 untuk setiap xE_k, dan

(iii) Terdapat M himpunan invarian terbesar dalam H



xEk|V(x)0



,

maka untuk t, setiap solusi Sistem (1) dengan syarat awal di dalam E termuat di k dalam M.

Akibat 6 Diberikan Sistem (1) dengan E Rn. Jika terdapat fungsi Lyapunov V, dengan (i) E_k 



xE|V(x)k



untuk suatu k0, merupakan himpunan terbatas,

(ii) V(x)0 untuk setiap xE_k, dan

(iii) H 



xEk |V(x)0



tidak memuat solusi kecuali titik ekuilibrium xˆ ,

maka xˆ stabil asimtotik lokal. Selanjutnya jika Ek E, maka titik ekuilibrium tersebut stabil asimtotik global.

Peran respon imun CTL dalam mengendalikan infeksi virus diselidiki dengan membandingkan model dinamika virus tanpa respon imun dan dengan respon CTL Perbandingan kedua model tersebut dilakukan secara analisis maupun simulasi numerik. Simulasi numerik terhadap masing-masing model dilakukan dengan bantuan software

Mathematica untuk beberapa nilai parameter dan nilai awal. Semua nilai parameter yang

digunakan dalam simulasi numerik mengacu pada Nowak dan May (2000), Adams (2004), Parelson (1992), dan Wodarz (2007) untuk mensimulasikan penyebaran virus HIV (human

immunodeficiency virus) yang menyerang sel CD4. HASIL DAN DISKUSI

1. Model Dinamika Virus Dalam Sel Tubuh Tanpa Respon Imun CTL

Dalam proses pemodelan dinamika virus tanpa respon imun CTL, populasi sel dalam tubuh dibagi menjadi dua sub populasi, yaitu Z menyatakan sub populasi sel tak terinfeksi dan

I menyatakan sub populasi sel terinfeksi. Untuk populasi virus bebas dinotasikan dengan V . Beberapa asumsi yang digunakan adalah populasi berdistribusi homogen, suatu sel akan terinfeksi jika terjadi kontak dengan virus, dan sel yang sudah terinfeksi pada akhirnya akan mati. Sel tak terinfeksi diproduksi tubuh dengan laju konstan



. Virus bereproduksi dengan rata-rata kepadatan kI per hari dan rata-rata kepadatan sel yang berhasil diinfeksi oleh virus adalah rZV per hari. Rata-rata kepadatan sel tak terinfeksi, sel terinfeksi, dan virus bebas yang mati berturut-turut adalah mZ,



I

, dan cV per hari. Secara matematis, dinamika virus tanpa respon imun dapat dimodelkan dalam bentuk sistem persamaan diferensial non linear berikut:

(4)

 mZrZV, t0 dt dZ  , rVZ  I, t0 dt dI



, (2) kIcV, t0 dt dV , 0

)

0 (

Z



,

I

(

0 )



I

₀,

V

(

0 )



V

₀, dengan



,

m

,

r

,



,k,

c

> 0 dan

Z

₀

,

I

₀

,

V

₀



0

. Rasio reproduksi dasar

c m rk R    0 , (3)

adalah rata-rata kepadatan sel terinfeksi baru yang dihasilkan dari satu sel terinfeksi ketika hampir semua kepadatan sel masih dalam keadaan tak terinfeksi Sistem (2) mempunyai dua titik ekuilibrium, yaitu





        , , ,0,0 m V I Z Q  , (4)













_           , , 1 , ₀ 1, ₀ 1 0 * * * * R r m R rk mc R m V I Z Q  . (5)

Titik

Q

disebut titik ekuilibrium bebas virus, karena sudah tidak terdapat virus dalam

tubuh, sedangkan

Q

_* disebut titik ekuilibrium endemik, karena virus masih menginfeksi sel-sel

dalam tubuh. Dapat dibuktikan bahwa jika

R

_o



1

, maka titik ekuilibrium

Q

stabil asimtotik global. Pada kondisi ini, dalam jangka panjang virus tidak akan menginfeksi sel tubuh lagi. Jika

1 

o

R

, maka

Q

menjadi tidak stabil, sedangkan

Q

* stabil asimtotik global. Dengan kata lain,

dalam jangka panjang dapat diprediksi masih terdapat virus bebas dan sel terinfeksi dalam tubuh. Selanjutnya, akan dikonstruksi dan dianalisis kestabilan titik ekuilibrium dari model dinamika virus dengan respon imun CTL.

2. Model Dinamika Virus Dalam Sel Tubuh Dengan Respon Imun CTL

CTL merupakan salah satu respon imun yang berperan mengidentifikasi dan menghancurkan sel terinfeksi, serta melenyapkan virus yang ada dalam sel tersebut. Interaksi antara CTL dan sel terinfeksi analog dengan model mangsa-pemangsa (predator-prey model), dengan CTL berperan sebagai pemangsa dan sel terinfeksi sebagai mangsa. Populasi CTL dalam tubuh dinotasikan dengan T. Pertumbuhan CTL dipengaruhi oleh rata-rata produksi CTL setiap waktu dan kematian alami. Rata-rata produksi CTL pada suatu waktu proporsional terhadap sel terinfeksi, yaitu dI. Laju kematian CTL adalah

n

, sehingga rata-rata kepadatan CTL yang mati adalah nT per hari. Dari uraian di atas, diperoleh sistem persamaan diferensial nonlinear yang merupakan model dinamika virus dalam sel tubuh dengan respon imun CTL sebagai berikut: rVZ mZ dt dZ   



, t 0, sIT I rVZ dt dI   



, t 0, kI cV dt dV   , t 0, (6) dI nT dt dT   0

)

0 (

Z



,

I

(

0 )



I

₀,

V

(

0 )



V

₀,

T

(

0 )



T

₀,

(5)

dengan



,

m

,

r

,



,k,

c

,

s

,d,

n

> 0 dan

Z

₀

,

I

₀

,

V

₀

,

T

₀



0

. Sistem (6) mempunyai dua titik ekuilibirum, yaitu titik ekuilibrium bebas virus



















,

0 ,

0 m

T

V

I

Z

P



(7)

dan titik ekuilibrium endemik





















V

kn

dc

V

k

c

V

r

m

T

V

I

Z

P

~

,

~

,

~

,

~



_~

,

~

,

~

,

~

, (8) dengan

R

₀



1

dan

V

~

adalah akar positif dari persamaan kuadrat

0 ~

~

:

)

~

(

₂ 2 2























sdc

k

n

sdcr

n

km

V

sdc

n

k

r

m

V

q





. (9)

Teorema berikut menjelaskan mengenai eksistensi dan kestabilan masing-masing titik ekuilibrium Sistem (6).

Theorema 7 Diberikan

R

₀ seperti pada Persamaan (3).

(i) Jika

R

_o



1

, maka Sistem (6) mempunyai satu titik ekuilibrium

P

, dengan

P

seperti pada (7). Titik tersebut stabil asimtotik global.

(ii) Jika

R

_o



1

, maka Sistem (6) mempunyai dua titik ekuilibrium, yaitu

P

dan

P

~

, dengan

P

dan

P

~

berturut-turut seperti pada (7) dan (8). Titik ekuilibrium

P

tidak stabil, sedangkan

P

~

stabil asimtotik global.

Bukti

Sistem (6) dapat diubah menjadi sistem yang lebih sederhana dengan transformasi berikut:









Z

t

kr

t

x

(

)



₂ ,









I

t

kr

t

y

(

)



₂ ,









V

t

r

t

z

(

)



,









T

t

s

t

w

(

)



, 2 0 0



krZ

x 

, ₀ ₂0



krI

y 

,



0 0

rV

z 

,



0 0

sT

w 

, (10)







c

, ₃









rk

,







m

,







n

, rk ds  '



,

sehingga Sistem (6) ekivalen dengan sistem berikut:

x











x



xz

, t 0,

y





xz



y



yw

, t0,

z





y





z

, t0, (11)

w



 '



y





w

, t 0,

x

(

0 )



x

₀,

y

(

0 )



y

₀,

z

(

0 )



z

₀,

w

(

0 )



w

₀,

dengan



,



,



,



,



'



0

dan

x

0

,

y

0

,

z

0

,

w

0



0

. Kondisi

R

0



1

ekivalen dengan

 



dan

1 

o

R

ekivalen dengan

 



. Sistem (11) mempunyai dua titik ekuilibrium, yaitu





_













,

0 ,

0 



w

z

y

x

P

(12)

dan





_



























z

w

z

y

x

P

~

'

,

~

,

~

,

~

,

~

,

~

,

~

, (13)

(6)





0 '

~

'

~

2 2







































z

. (14)

(i) Diberikan fungsi Lyapunov pada



₀



{(

,

)

4

:

0 ,

,

0 }







R

x

y

z

w

z

y

x

, yaitu













_























₀ 2 2

'

2

1

2

1 ,

,

y

z

w

x

y

z

w

x





,

dengan

x







. Dari fungsi tersebut diperoleh

0





2







2









2 

2

'

)

(

,

y

z

w

x

z

x

w

x























_.

Karena z 0 dan

x











, sehingga ₀



x,y,z,w



0 untuk setiap



x

,

y

,

z

,

w







0. Persamaan 0



x,y,z,w



0 dipenuhi jika dan hanya jika x  x,

0 

y

, z 0, dan w0. Sehingga berdasarkan Akibat 6,

P

stabil asimtotik global pada



0.

(ii) Diberikan fungsi Lyapunov pada 

{(

x

,

y

,

z

,

w

)



R

4

:

x

,

y

,

z

,

w



0 }

, yaitu



 









~



2

'

2

1 ln

~

ln

~

ln

~

,

y

z

w

x

y

x

z

w

x























,

dengan

~

x

,

y

~

,

~

z

,

w

~

diberikan pada Persamaan (13). Dari fungsi tersebut diperoleh



x

,

y

,

z

,

w







_

_

2 2

_

_~

_

2 ' 3 ~ ~ ~ ~ ~ _w _w y x xz x x z y z x x x x _                    

Berdasarkan pertidaksamaan aritmatika-geometri diperoleh



3 ~

~

2





y

x

xz

x

z

y

.

Akibatnya,







x

,

y

,

z

,

w





0

untuk setiap



x

,

y

,

z

,

w







. Persamaan







x

,

y

,

z

,

w





0

dipenuhi jika dan hanya jika x x~,

y



y

~

_,z z~

_{, dan}

ww~. Sehingga berdasarkan Akibat 6,

P

stabil asimtotik global pada



₀. Teorema 7 menjelaskan bahwa jika

R

₀



1

, maka dalam jangka panjang sudah tidak terdapat virus bebas dan sel terinfeksi dalam tubuh. Jika

R

₀



1

, maka dalam jangka panjang masih terdapat virus bebas, sel terinfeksi, dan CTL dalam tubuh. Pada kondisi ini diperoleh

₂ 2 * 2 * *) ( sdc k n sdcr n km V sdc n k r m V V q



 







       

_

1

_

_

0 1

_

_

0 1

_

2 0                         R sdcr n km R r m sdc n k r m R r m   ₂ ₀



₀ 1



0 2    R R r m .

Karena q

 

V~ 0, maka V ~ V_*. Oleh karena itu, respon imun CTL berperan menurunkan kepadatan virus dalam tubuh. Dari (5) dan (8) diperoleh





V

r

R

m

I

V

~

1 ~

ˆ

~

*



*



0



,

sehingga respon imun CTL juga menurunkan kepadatan sel terinfeksi dengan rasio yang sama.

Selanjutnya, dari pertidaksamaan ~ _* 



R₀1



r m V

(7)

0 ~ mR V r m 



rk c V r m





  ~



* ~ Z Z  ,

sehingga respon imun CTL meningkatkan kepadatan sel tak terinfeksi dalam tubuh. Dengan kata lain, respon imun CTL berperan menurunkan tingkat infeksi yang disebabkan oleh virus. Dinamika virus dalam sel tubuh dan bagaimana peran respon imun CTL dalam mengendalikan infeksi virus juga dapat dilihat secara geometris, yaitu dengan melakukan simulasi terhadap Sistem (2) dan (6) dengan nilai awal dan nilai parameter tertentu.

3. Simulasi Numerik

Diberikan nilai-nilai parameter untuk Sistem (2) dan (6), yaitu



10,

m



0 ,

01

,

4

10

2 





r

,





0 ,

7

, k 100, c5,

s



0 ,

01

,

d



0 ,

7

, dan

n



0 ,

1

. Nilai parameter



,

m

,

r

,



,k,

c

,

s

,d, dan

n

diperoleh dari Nowak dan May (2000), Adams (2004), dan Perelson (1992) untuk mensimulasikan penyebaran virus HIV (human imunnodeficiency virus) yang menyerang sel T CD4+.

Berdasarkan nilai parameter di atas, diperoleh

R

₀



5 ,

71429

dan

R

₁



1 ,

05714

, sehingga

R 

₁

R

₀. Dengan menggunakan sofware Mathematica, diperoleh grafik

Z

(t

)

,

I

(t

)

, dan

V

(t

)

terhadap waktu

(t

)

dari Sistem (2) yang dapat dilihat pada Gambar 1. Dalam simulasi ini digunakan nilai awal



Z

₀

,

I

₀

,

V

₀







1000

,

0 ,

001 

sel/mm3. Gambar 1 menunjukkan bahwa untuk kedua nilai awal yang diberikan, populasi sel tak terinfeksi, sel terinfeksi, dan virus bebas mengalami osilasi dan dalam jangka panjang konvergen menuju ke titik ekuilibrium endemik

Q

_*





175 ,

11 ,

786 ,

235 ,

714 

sel/mm3. Hal ini menunjukkan bahwa populasi sel terinfeksi dan virus bebas tetap ada. Dengan kata lain, infeksi virus tetap menyebar dalam tubuh. Gambar 1 juga menunjukkan bahwa populasi sel terinfeksi dan virus bebas mulai mengalami peningkatan pada saat kepadatan sel tak terinfeksi menurun. Demikian juga sebaliknya, pada saat populasi sel tak terinfeksi mulai mengalami peningkatan kembali, populasi sel terinfeksi dan virus bebas akan menurun.

Sifat kestabilan global dari titik ekuilibrium

Q

_* diilustrasikan pada Gambar 2. Gambar tersebut menunjukkan bahwa untuk beberapa pengambilan nilai awal yang berbeda, populasi sel dan virus tetap konvergen menuju ke titik ekuilibrium endemik

Q

_*. Sebagai contoh, perhatikan trayektori untuk nilai awal



Z

₀

,

I

₀

,

V

₀







50 ,

550 ,

0 ,

001 

sel/mm3 (warna merah) dan



800 ,

900 ,

0 ,

001 

sel/mm3 (warna biru). Kedua trayektori tersebut bergerak dari nilai awal menuju ke titik ekuilibrium

Q

_*.

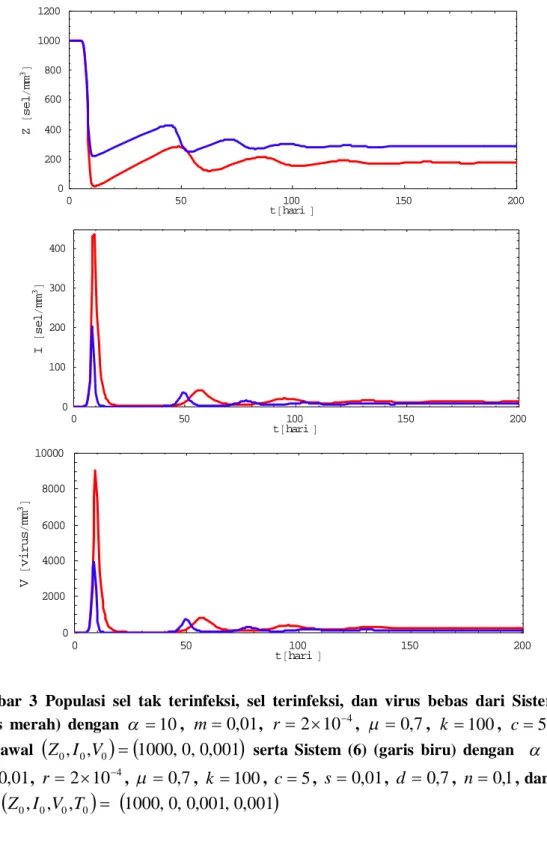
Gambar 3 memperlihatkan pengaruh respon CTL terhadap infeksi virus. Gambar 3 menunjukkan bahwa tanpa adanya respon imun, angka kepadatan tertinggi sel terinfeksi dan virus bebas dalam tubuh berturut-turut mencapai sekitar 460 sel/mm3 dan

9 

,

1

10

3 virus/mm3, serta populasi konvergen menuju ke titik ekuilibrium

Q

*. Untuk model dinamika virus dengan

respon CTL, angka kepadatan tertinggi sel terinfeksi dan virus bebas berturut-turut mencapai sekitar 200 sel/mm3 dan

3 

,

9

10

3 virus/mm3, serta populasi konvergen menuju ke titik ekuilibrium P~



284,843,6,277,125,535,43,937



sel/mm3. Dengan demikian, respon CTL berperan menurun kepadatan sel terinfeksi dan virus bebas pada saat puncak epidemi, serta meningkatkan kepadatan sel tak terinfeksi dan menurunkan kepadatan virus bebas dan sel terinfeksi dalam tubuh pada titik ekuilibrium.

KESIMPULAN

Dari pembahasan di atas, kestabilan global titik ekuilibrium dari model dinamika virus tanpa dan dengan respon imun tergantung dari rasio reproduksi dasar

 

R

₀ . Jika

R

₀



1

, maka

(8)

titik ekuilibrium endemik yang memiliki sifat stabil asimtotik global. Selanjutnya, dengan membandingkan model dinamika virus tanpa dan dengan respon imun CTL, dapat disimpulkan bahwa respon imun CTL mempunyai pengaruh dalam mengendalikan infeksi virus yang terjadi, yaitu mampu menurunkan kepadatan sel terinfeksi dan virus bebas dalam tubuh.

DAFTAR PUSTAKA

Adams, B. M., Banks, H.T., Davidian, M., Hee-Dae Kwon, Tran H. T. 2004. Dynamic Multidrug Therapies For HIV: Optimal And STI Control Approaches, Mathematical

Biosciences And Engineering, Volume 1, Number 2, pp.223-241.

Kurdhi, N. A. and Aryati, L. 2010. Global Stability of Virus Dynamics Model with CTL Response, Department of Mathematics UGM, Yogyakarta.

Luenberger, G. D. 1979. Introduction to Dynamic Systems Theory, Models, and Applications, John Wiley & Sons, New York.

Nowak, M. A. and May, R. M. 2000. Virus Dynamics, Oxford University Press, Inc., New York.

Perelson, A. S., Kirschner, D. E., and Boer, R. D. 1993 Dynamics of HIV infection of CD4+ T Cells, Mathematical Biosciences 114:81-125.

Perko, L. 1991. Differential Equations and Dynamical Systems, Springer-Verlag New York, Inc.

Pruss, J., Zacher, R., and Schnaubelt, R. 2008. Global Asymptotic Stability of Equilibria in Models for Virus Dynamics, Math. Model. Nat. Phenom. Vol. 3, No. 7, pp. 126-142.

Verhulst, Ferdinand. 1996. Nonlinear Differential Equations and Dynamical Systems, 2nd

Edition.

Wodarz, D. 2007. Killer Cells Dynamics, Mathematical and Computational Approaches to Immunolog. Springer-Verlag, New York.

(9)

Lampiran: Grafik Simulasi Numerik 0 50 100 150 200 thari  0 200 400 600 800 1000 1200 1400 Z , I , V  l e s  m m 3

Gambar 1 Populasi sel tak terinfeksi (garis hitam), sel terinfeksi (garis merah), dan virus bebas (garis biru) dari Sistem (2) dengan nilai parameter



10,

m



0 ,

01

,

4

0

2 





r

,





0 ,

7

, k 100, c5, dan nilai awal



Z

₀

,

I

₀

,

V

₀







1000

,

0 ,

001 

0 5000 10000 15000 20000 V 0 200 400 600 800 Z 0 250 500 750 1000 I 0 5000 10000 15000

Gambar 2 Potret fase Sistem (2) dengan



10,

m



0 ,

01

,

_r

_

2 _

0

4

,





0 ,

7

, k 100, dan c5, dengan beberapa nilai awal

(10)

0 50 100 150 200 thari 0 200 400 600 800 1000 1200 Z  l e s  m m 3

0 50 100 150 200 thari  0 100 200 300 400 I  l e s  m m 3

0 50 100 150 200 thari 0 2000 4000 6000 8000 10000 V  s u r i v  m m 3

Gambar 3 Populasi sel tak terinfeksi, sel terinfeksi, dan virus bebas dari Sistem (2) (garis merah) dengan