Developing statistical thinking2
Teks penuh
Gambar
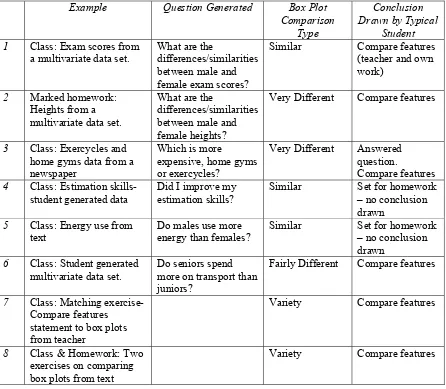
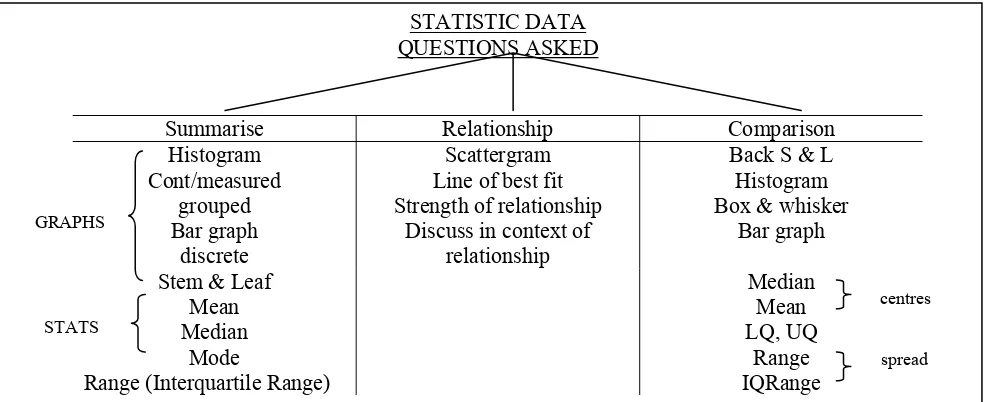
Garis besar
Dokumen terkait
Kelompok agamawan yang mencoba untuk menarik-narik agama ke dalam kaukus kekuasaan, untuk meraih kekuasaan dalam konteks semacam ini dapat disebut sebagai politisasi agama
kedua shot itu sebagai satu kesatuan yang utuh dan juga langsung terlihat keberlanjutan aksi bisa tetap terjaga dari 2 sambungan tersebut.. cutaway dapat digunakan untuk:
Berdasar wawancara peneliti dengan pimpinan proyek dapat diketahui bahwa pada awal pengerjaan suatu proyek, bendahara dan staf (umumnya bagi yang baru pertama
Maka kami mengundang saudara untuk melakukan pembuktian kualifikasi perusahaan saudara dengan membawa dokumen-dokumen yang telah diupload yang akan diadakan pada:. Hari/ Tanggal
Tujuan dari penelitian ini adalah untuk mengetahui apakah terdapat perbedaan efek kenyang pada subjek dengan status gizi normal, setelah mengkonsumsi makanan SSKInd dan makanan
Pokja ULP/Panitia Pengadaan Barang/Jasa Pengadaan Pakaian Dinas Lapangan Beserta Kelengkapannya Program Peningkatan Disiplin Aparatur. Dinas Pemadam Kebakaran Kota Makassar
Dalam penelitian ini, bagaimana koordinasi dan sub sistem yang terlibat terhadap kelompok sasaran dalam pelaksanaannya sehingga memberikan pengaruh baik
maka Pokja Pengadaan Barang/Jasa pada Unit Layanan Pengadaan Barang/Jasa Kabupaten Aceh Barat Daya Tahun Anggaran 2016 mengumumkan Pemenang Paket tersebut di atas dengan rincian