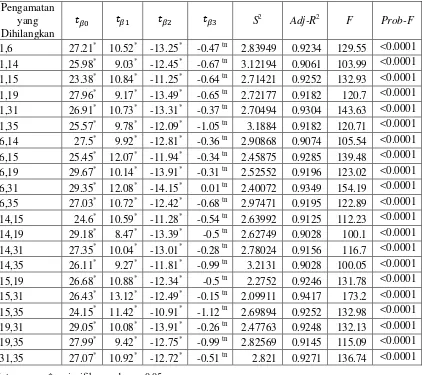
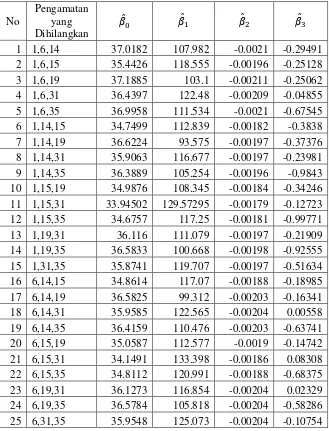
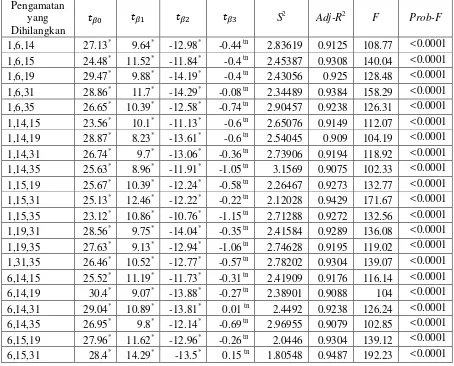
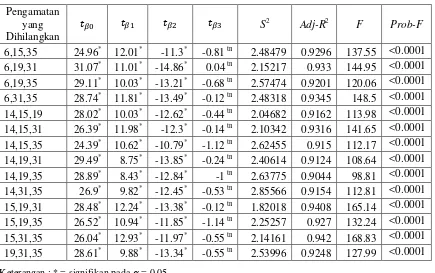
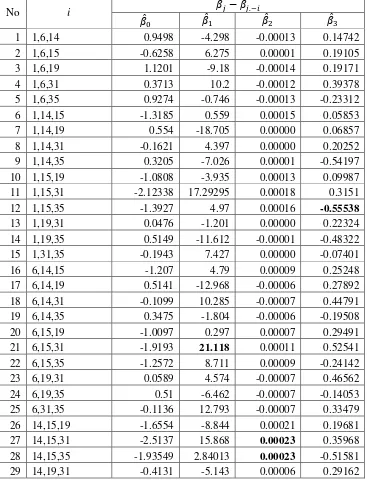
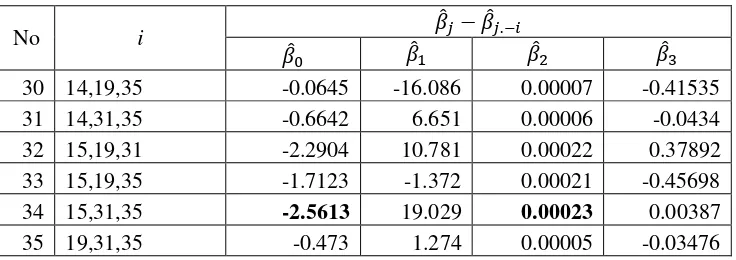
DIAGNOSA PENGAMATAN BERPENGARUH MENGGUNAKAN DFBETAS DAN KONSTRUKSI VARIABEL PADA ANALISIS REGRESI LINIER BERGANDA
Teks penuh
Gambar
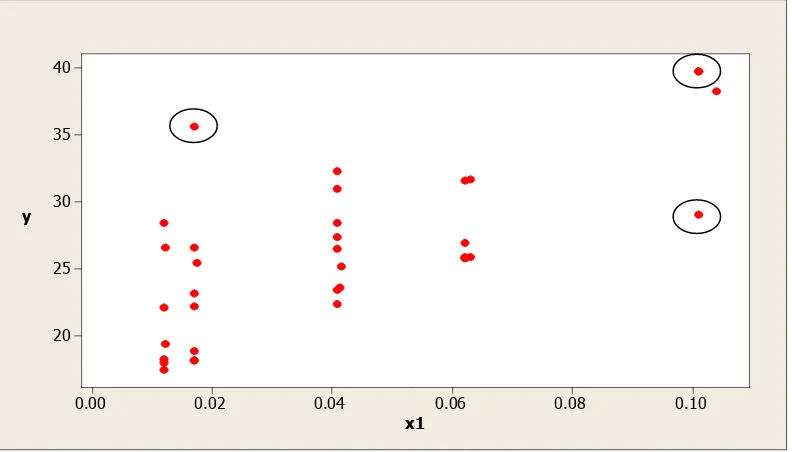
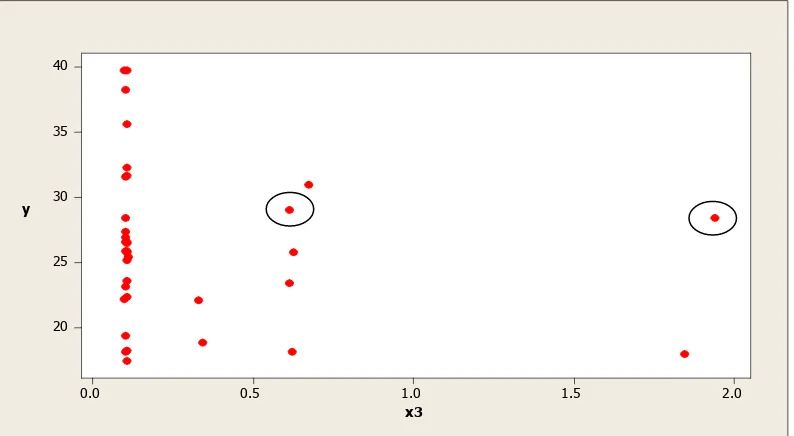
Dokumen terkait
Berdasarkan masalah tersebut maka penelitian ini dilakukan menggunakan data mining yang dimodelkan dengan algoritma regresi linier berganda yang bertujuan untuk
Berdasarkan masalah tersebut maka penelitian ini dilakukan menggunakan data mining yang dimodelkan dengan algoritma regresi linier berganda yang bertujuan untuk
Model regresi linier berganda data longitudinal akan diaplikasikan pada data kemiskinan pada 23 Kabupaten/Kota yang ada di Provinsi Sulawesi Selatan tahun 2004-2008
Persamaan regresi linier berganda yang mengandung pencilan dengan menggunakan estimasi regresi robust MM-estimator yang diperoleh dalam tugas akhir ini adalah:. Robust Regression
Selain itu, Budiman dan Akhlakulkarimah pada tahun 2016 juga telah melalukan penelitian prediksi curah hujan menggunakan metode regresi linier berganda dengan
Dalam Prediksi Jumlah Pelanggan dan Persediaan Barang Menggunakan Metode Regresi linier berganda Pada Bali Orchid terdapat menu-menu yang dapat diakses oleh User
melakukan pengujian hipotesis mengenai satu para meter regresi, semua parameter regresi dan beberapa parameter regresi pada analisis regresi linier berganda.. 6 menemukan
Penentuan Faktor Cuaca yang Berpengaruh Terhadap Curah Hujan dengan Metode Regresi Linier Berganda dan Metode Algoritma Genetika Studi Kasus : Kota Tanjungpinang, Skripsi..