Pengaruh vaksinasi terhadap dinamika populasi pada model SIR (Susceptible-Infected-Recovered)

(1)

ABSTRAK

SUBRO MULISI. Pengaruh Vaksinasi terhadap Dinamika Populasi pada Model SIR (Susceptible-Infected-Recovered). Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan ALI KUSNANTO.

Model SIR digunakan untuk memodelkan penyebaran suatu penyakit dalam suatu populasi tertutup berdasarkan asumsi-asumsi tertentu. Pada penelitian ini, model SIR dirumuskan dengan memasukkan faktor vaksinasi. Dari hasil analisis model, dihasilkan dua titik kesetimbangan yaitu titik kesetimbangan bebas penyakit dan titik kesetimbangan endemik.

(2)

ABSTRACT

SUBRO MULISI. The Effect of Vaccination in Population Dynamics with SIR

(Susceptible-Infected-Recovered) Model. Supervised by ENDAR HASAFAH NUGRAHANI and ALI

KUSNANTO.

SIR model can be used to model the spread of diseases in a closed population based on certain assumptions. In this research, the SIR model is formulated by including the factor of vaccination. As the result, the model has been shown to have two equilibrium points, i.e. disease free and endemic equilibrium.

(3)

I.

PENDAHULUAN

1.1 Latar Belakang

Model matematika merupakan salah satu alat yang dapat membantu mempermudah penyelesaian masalah dalam kehidupan nyata. Masalah-masalah tersebut dapat dibawa ke dalam model matematis dengan menggunakan asumsi-asumsi tertentu. Selanjutnya, dari model yang didapat akan dicari solusinya, baik dengan cara analitis maupun secara numerik.

Salah satu permasalahan pada kehidupan nyata adalah mengenai penyebaran suatu penyakit, di mana individu yang terinfeksi akan mempunyai kekebalan dalam jangka waktu tertentu, contohnya adalah penyakit campak dan influenza. Penyakit measles (campak), mumps (gondong), rubella (campak Jerman), dan poliomyelitis (polio) merupakan penyakit infeksi yang sangat berbahaya. Penyakit tersebut disebabkan oleh virus yang dapat menyebar melalui kontak langsung dengan penderita, udara batuk atau bersin, dan kotoran manusia. Anak-anak yang biasanya lebih sering terjangkit penyakit tersebut. Oleh karena itu, salah satu upaya yang dilakukan UNICEF untuk mencegah meluasnya penyakit tersebut adalah dengan melakukan program vaksinasi (UNICEF 2007).

Perkembangan ilmu pengetahuan di bidang matematika juga turut memberikan peranan yang penting dalam mencegah meluasnya penyebaran penyakit tersebut. Peranan tersebut berupa penyelesaian masalah tentang penyebaran penyakit. Selanjutnya, masalah penyebaran penyakit ini akan dimodelkan secara matematis menggunakan tipe model penyebaran penyakit SIR (Suspected-Infected-Recovered). Secara umum model epidemi SIR ini dapat disajikan sebagai sistem persamaan diferensial autonomous/mandiri. Sistem persamaan diferensial mandiri epidemi SIR ini secara garis besar menggambarkan alur penyebaran penyebaran penyakit dari subpopulasi individu susceptible (rentan) menjadi infected (terinfeksi) melalui kontak langsung maupun perantara lain. Selanjutnya individu infected yang mampu bertahan terhadap penyakit akan sembuh dan memasuki subpopulasi recovered (sembuh).

Model SIR selanjutnya digunakan untuk memodelkan penyebaran penyakit yang bersifat endemik. Berdasarkan data dari

WHO, penyebaran penyakit dapat ditekan setelah adanya program vaksinasi (WHO 2007). Sampai saat ini, program vaksinasi masih dipercaya sebagai cara yang paling efektif dalam menekan penyebaran penyakit. Oleh karena itu, vaksinasi harus diperhatikan dalam model sebagai upaya untuk mencegah meluasnya penyakit.

Mobilitas atau perpindahan populasi dari suatu wilayah ke wilayah lain dapat terjadi dalam suatu wilayah. Mobilitas tersebut secara umum disebut sebagai migrasi. Adanya migrasi dapat memungkinkan terjadinya penyebaran penyakit yang dibawa oleh populasi yang masuk atau keluar dari suatu wilayah. Oleh karena itu, pengaruh migrasi perlu diperhatikan dalam model. Namun, dalam populasi tertutup, migrasi tidak terjadi dalam wilayah tersebut sehingga tidak diperhatikan dalam model.

Pada karya ilmiah ini, akan dianalisis sebuah model SIR yang dikembangkan oleh Kermack dan McKendrick (Makinde 2007). Model tersebut akan dipengaruhi faktor adanya vaksinasi dengan tingkatan yang tinggi atau rendah serta faktor tidak adanya vaksinasi yang akan ditentukan kestabilan di titik tetapnya.

1.2 Tujuan Penulisan

Tujuan dari penulisan karya ilmiah ini adalah untuk merumuskan model SIR dengan pengaruh vaksinasi serta pengaruhnya terhadap dinamika populasi dan melakukan simulasi terhadap nilai-nilai parameter yang mempengaruhinya.

1.3 Sistematika Penulisan

(4)

II.

LANDASAN TEORI

2.1 Sistem Persamaan Diferensial Mandiri

Perhatikan sistem persamaan diferensial (SPD) berikut:

,

(2.1)

,

dan adalah fungsi kontinu dari dan dengan turunan parsial pertama kontinu, dengan laju perubahan dan dinyatakan dengan fungsi eksplisit dari dan sendiri dan tidak mengandung . SPD (2.1) disebut sebagai sistem persamaan diferensial autonomous/mandiri.

[Farlow 1994]

2.2 Titik Tetap

Misalkan diberikan persamaan diferensial (SPD) sebagai berikut:

, . Titik disebut titik tetap jika memenuhi

. Titik tetap disebut juga titik kritis atau titik kesetimbangan. Untuk selanjutnya akan digunakan istilah titik tetap.

[Tu 1994]

2.3 Pelinearan

Misalkan:

, ,

Andaikan , adalah titik tetap dari persamaan di atas, maka , dan

, . Misalkan dan

maka didapatkan: , , , , , , , , , , , ,

Dalam bentuk matriks:

, ,

Matriks

,

disebut

matriks Jacobi pada titik tetap , . Karena , , maka dapat diabaikan sehingga didapat persamaan linear:

.

[Strogatz 1994]

2.4 Nilai Eigen dan Vektor Eigen

Misalkan matriks berukuran . Suatu vektor tak nol di disebut vektor eigen dari jika untuk suatu skalar, yang disebut nilai eigen dari berlaku:

. Vektor disebut vektor eigen yang bersesuaian dengan nilai eigen .

Untuk mencari nilai eigen dari matriks yang berukuran , maka persamaan (2.4) dapat ditulis sebagai berikut:

. Dengan adalah matriks identitas berukuran . Persamaan (2.5) mempunyai solusi tak nol jika dan hanya jika:

. Persamaan (2.6) disebut persamaan karakteristik dari .

[Tu 1994]

2.5 Kestabilan Titik Tetap

Diberikan sistem persamaan differensial sembarang:

, . Analisis kestabilan titik tetap dilakukan melalui matriks Jacobi, yaitu matriks . Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigennya, yaitu dengan , , , … yang diperoleh dari

(5)

Secara umum kestabilan titik tetap mempunyai tiga perilaku sebagai berikut: 1. Stabil, jika

a. Setiap nilai eigen real adalah negatif ( untuk semua )

b. Setiap komponen bagian real dari nilai eigen kompleks, lebih kecil atau sama dengan nol ( untuk semua ).

2. Takstabil, jika

a. Ada nilai eigen real yang positif ( untuk suatu ).

b. Ada komponen bagian real dari nilai eigen kompleks, lebih besar dari nol ( untuk suatu ).

3. Sadel, jika perkalian dua buah nilai eigen real sembarang adalah negatif ( , untuk dan sembarang). Titik tetap sadel ini bersifat takstabil.

[Tu 1994]

2.6 Bilangan Reproduksi Dasar

Bilangan reproduksi dasar adalah rata-rata banyaknya individu yang rentan terinfeksi secara langsung oleh individu lain yang telah terinfeksi bila individu yang telah terinfeksi tersebut masuk ke dalam populasi yang seluruhnya masih rentan. Bilangan reproduksi dasar dilambangkan dengan .

Beberapa kondisi yang akan timbul, yaitu 1. Jika , maka penyakit akan

menghilang.

2. Jika , maka penyakit akan menetap.

3. Jika , maka penyakit akan meningkat menjadi wabah.

[Giesecke 1994]

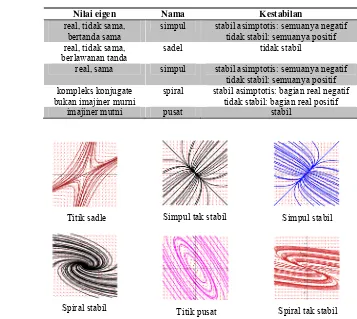
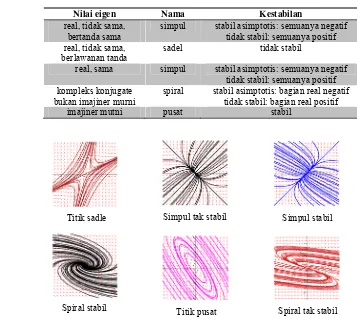
Pada Tabel 1 berikut diberikan tabel jenis-jenis kestabilan titik tetap berdasarkan nilai eigennya serta pada Gambar 1 diberikan juga gambar jenis-jenis kestabilan titik tetap [Bellomo & Preziosi 1995]:

Tabel 1. Kriteria kestabilan berdasarkan nilai eigen

Nilai eigen Nama Kestabilan

real, tidak sama, bertanda sama

simpul stabil asimptotis: semuanya negatif tidak stabil: semuanya positif real, tidak sama,

berlawanan tanda

sadel tidak stabil

real, sama simpul stabil asimptotis: semuanya negatif tidak stabil: semuanya positif kompleks konjugate

bukan imajiner murni

spiral stabil asimptotis: bagian real negatif tidak stabil: bagian real positif imajiner mutni pusat stabil

Gambar 1. Jenis-jenis kestabilan titik tetap

Simpul stabil Simpul tak stabil

Titik pusat Titik sadle

Spiral stabil _{Spiral tak stabil}

(6)

III.

PEMBAHASAN

3.1 Konstruksi Model

3.1.1 Model SIR

Model SIR yang digunakan dalam tulisan ini disusun oleh Kermack and McKendrick. Model SIR (Susceptibles, Invectives, Recovered) pada awalnya dikembangkan untuk mengetahui laju penyebaran dan kepunahan suatu wabah penyakit dalam populasi tertutup dan bersifat epidemik (Makinde 2007). Pada tulisan ini dibahas mengenai pembentukan model SIR berdasarkan asumsi yang dibuat. Setelah model terbentuk, kemudian dicari solusi analitis dan titik tetapnya, yang selanjutnya diinterpretasikan dalam permasalahan yang sesungguhnya dalam kehidupan nyata. Dalam hal ini adalah mengenai perilaku penyebaran penyakit dan eksistensinya, yaitu titik tetap bebas penyakit dan titik tetap endemik.

Penyebaran penyakit dalam suatu populasi diasumsikan memiliki jumlah konstan dan dalam satu periode waktu wabah. Pada saat t misalkan suatu populasi terdiri dari:

Susceptibles S(t): adalah subpopulasi di

mana anggotanya terdiri dari orang-orang yang rentan terkena penyakit tersebut.

InfectivesI(t): adalah subpopulasi di mana anggotanya terdiri dari orang-orang yang sudah terjangkit penyakit tersebut.

RecoveredR(t): adalah subpopulasi yang

telah sembuh dari penyakit tersebut. Dengan proporsi

Pada pembentukan model SIR diberikan berbagai asumsi yang terdiri dari:

1) Populasi tertutup (tidak ada proses migrasi).

2) Terjadi proses kelahiran dan kematian.

3) Laju kelahiran sama dengan laju kematian (jumlah populasi tetap). 4) Penyakit dapat disembuhkan.

5) Setiap individu yang belum terserang penyakit masuk ke subpopulasi susceptibles (rentan terserang). 6) Individu yang sembuh mempunyai

kekebalan tetap.

7) Penyakit menular melalui kontak langsung antara individu rentan dengan penderita.

8) Tidak ada masa inkubasi apabila terjadi proses penularan.

9) Masa terjangkit yang cukup lama.

Diasumsikan terdapat kontak yang tetap dari subpopulasi S dan I dalam populasi tersebut dan angka susceptible S(t) ditambah dengan bilangan konstan ȝ. Bilangan konstan

ȝ melambangkan kondisi di mana muncul kelahiran baru dan bayi yang baru lahir otomatis masuk dalam kondisi rentan. Karena laju kelahiran sama dengan laju kematian, maka nilai kedua laju sama yaitu ȝ. Misalkan laju penularan penyakit adalah , maka dalam satu waktu laju dari susceptibles menjadi infective adalah:

. dengan dan ȝ adalah konstan positif dan ȝS adalah jumlah kematian pada subpopulasi S. Jika > 0 adalah laju kesembuhan dari

infected menjadi recovered, maka:

. dengan ȝI adalah jumlah kematian pada subpopulasi I, dan laju perubahan subpopulasi recovered menjadi:

. dengan ȝR adalah jumlah kematian dari subpopulasi R.

Gambar 2. Model SIR

3.1.2 Model SIR dengan Pengaruh Vaksinasi

Selanjutnya, program vaksinasi diperhatikan dalam model (Makinde 2007). Dalam hal ini, vaksin hanya diberikan pada individu yang baru lahir atau masih dalam usia anak-anak. Diasumsikan bahwa efisiensi vaksinasi adalah 100% yang berarti setiap individu yang telah mendapat vaksin akan kebal dari penyakit. Kekebalan yang terjadi karena vaksin bersifat permanen yang berarti individu tersebut tidak dapat terinfeksi oleh penyakit yang dimaksud.

Diasumsikan rasio jumlah individu yang memperoleh vaksin adalah . Individu yang memperoleh vaksin akan kebal dari penyakit dan memasuki subpopulasi R. Jumlah individu yang memperoleh vaksin proporsional dengan jumlah kelahiran . Dengan demikian, jumlah

(7)

individu yang kebal dari penyakit karena telah memperoleh vaksin adalah .

Jumlah individu yang tidak mendapat

vaksin adalah .

Selanjutnya individu yang tidak mendapatkan vaksin akan memasuki subpopulasi S dan berpotensi untuk terinfeksi penyakit.

Alur perpindahan individu susceptible menjadi infected kemudian sembuh dan memasuki subpopulasi recovered disajikan pada Gambar 3.2. Nilai parameter dari , , dan adalah positif. Batas dari laju vaksinasi adalah .

Laju perubahan individu pada subpopulasi S dapat diekspresikan sebagai:

.

Gambar 3. Dinamika populasi model SIR dengan pengaruh vaksinasi

Laju perubahan individu pada subpopulasi I dapat dinyatakan sebagai:

. Laju perubahan individu pada subpopulasi R adalah:

.

dengan , , dan .

3.2 Kesetimbangan Model

Pada persamaan (3.4) dan (3.5) variabel R tidak muncul. Hal ini menunjukkan bahwa jumlah individu pada subpopulasi R tidak mempengaruhi laju perubahan jumlah individu pada subpopulasi S maupun I. Dari

proporsi , didapat

sehingga penyelesaian untuk R dapat diperoleh dengan

mudah jika penyelesaian untuk S dan I sudah diperoleh. Dengan demikian, berdasarkan kondisi tersebut, persamaan (3.4), (3.5), dan (3.6) dapat diperhatikan sebagai:

(3.7)

Titik tetap persamaan (3.7) dapat diperoleh dengan menentukan:

(3.8)

Dari persamaan (3.8) di atas diperoleh dua titik tetap:

1. Titik tetap yang pertama diekspresikan sebagai:

,

Nilai I = 0 berarti tidak ada individu pada kelompok I yang dapat menyebabkan penyakit. Titik tetap ini juga dapat dituliskan dengan

, .

2. Titik tetap yang kedua diekspresikan sebagai:

, (bukti lihat Lampiran 1).

Titik tetap ini bisa dituliskan sebagai , , nilai yang tidak nol menunjukkan bahwa terdapat individu pada kelompok I yang dapat menyebarluaskan penyakit dan menyebabkan endemik.

3.3 Analisis Kestabilan Titik Tetap

Analisis kestabilan ditentukan berdasarkan nilai eigen dari matriks Jacobian yang diperoleh dari metode linearisasi. Matriks Jacobian yang diperoleh dari persamaan (3.7) adalah:

. Kestabilan dari titik-titik tetap dan ditentukan berdasarkan nilai eigen dan matriks Jacobian di titik-titik tersebut.

3.3.1 Kestabilan di Titik Tetap

Matriks Jacobian di titik , adalah:

. (bukti lihat Lampiran 2)

dengan S σ . Nilai eigen dari matriks Jacobian (3.10) diperoleh dengan menggunakan persamaan karakteristik | Ι| yaitu:

dan

E0 akan bersifat stabil asimptotis jika untuk i = 1, 2. Nilai mengakibatkan nilai . Jika

maka mengakibatkan:

S I R

Vaksin

(8)

. di mana merupakan bilangan reproduksi

vaksinasi , sehingga titik akan bersifat stabil asimptotis untuk . Namun, jika

maka titik akan tidak stabil.

3.3.2 Bilangan Reproduksi Vaksinasi

Untuk mengetahui tingkat penyebaran suatu penyakit diperlukan suatu parameter tertentu. Parameter yang biasa digunakan dalam masalah penyebaran penyakit adalah bilangan reproduksi vaksinasi. Menurut Hethcote (2000), bilangan reproduksi merupakan bilangan yang menunjukkan jumlah individu susceptible yang dapat menderita penyakit yang diakibatkan oleh satu individu infected. Bilangan reproduksi selanjutnya merupakan bilangan reproduksi pada kasus yang memperhatikan faktor vaksinasi.

Berdasarkan titik tetapnya, bilangan reproduksi vaksinasi dapat diekspresikan sebagai:

. (bukti lihat Lampiran 3).

Jika maka untuk ∞, yang berarti bahwa jumlah penderita penyakit berangsur-angsur semakin berkurang sehingga penyakit akan menghilang dari populasi dan tidak terjadi endemik. Jika maka

, yang berarti jumlah penderita penyakit berangsur-angsur semakin bertambah sehingga penyakit akan meluas dan menjadi endemik.

Berdasarkan definisi titik tetap, nilai pada persamaan (3.12) didekati dengan titik tetap bebas penyakit yaitu . Sehingga nilai

dapat diekspresikan dengan:

. Dari persamaan (3.13) dapat didefinisikan tingkat vaksinasi minimum yang diperlukan untuk mencegah menyebarnya penyakit. Tingkat vaksinasi merupakan proporsi kelahiran yang mendapatkan vaksin. Tingkat vaksinasi minimum yang diperlukan untuk mencegah menyebarnya penyakit dinotasikan dengan . Penyakit akan berangsur-angsur menghilang dari populasi untuk . Dengan demikian, untuk diperoleh tingkat vaksinasi minimum yaitu:

Dari persamaan yang diperoleh di atas, tingkat vaksinasi yang diberikan harus lebih besar dari agar penyakit dapat dicegah penyebarannya. Jika tingkat vaksinasi yang diberikan lebih besar dari tingkat vaksinasi minimum maka:

(3.14)

Persamaan (3.14) mengakibatkan bahwa jumlah individu susceptible yang dapat terinfeksi penyakit yang diakibatkan oleh satu individu infected dengan tingkat pemberian vaksinasi akan lebih kecil jika dibandingkan saat diberikan vaksin pada tingkat . Oleh karena itu, tingkat vaksinasi yang diberikan harus lebih besar dari agar jumlah penderita dapat ditekan sekecil mungkin dan penyakit dapat menghilang dari populasi.

Selanjutnya, jika tingkat vaksinasi maka:

(3.15)

Persamaan (3.15) menyebabkan penyakit akan menjadi endemik jika tingkat vaksinasi yang diberikan lebih kecil dari tingkat vaksinasi minimum .

3.3.3 Kestabilan di Titik Tetap

. Karena titik tetap :

,

matriks Jacobian pada persamaan (3.16) menjadi:

. Titik tetap diekspresikan menggunakan definisi bilangan produksi vaksinasi menjadi:

(9)

7

, , .

Dengan menggunakan persamaan (3.18), diperoleh nilai eigen dari matriks Jacobian (3.17) yaitu:

,

(bukti lihat Lampiran 2).

Dari persamaan (3.18), titik endemik hanya akan muncul jika sedangkan nilai eigen Ȝ1,2 akan berupa bilangan real negatif atau bilangan kompleks dengan bagian real bernilai negatif untuk:

. Kondisi (3.19) menyebabkan titik tetap Ee akan bersifat stabil asimptotis.

Berikut adalah tabel kondisi kestabilan dari kedua titik tetap yang diperoleh.

Tabel 2. Kondisi kestabilan titik tetap Kondisi Stabil asimptotis Tidak stabil Tidak stabil Stabil asimptotis

Dari Tabel 2 dapat dilihat bahwa kondisi kestabilan dari titik tetap yang diperoleh saling berbeda. Ketika titik tetap yang pertama stabil asimptotis, titik tetap yang kedua tidak stabil dan ketika titik tetap yang pertama tidak stabil, titik tetap yang kedua stabil asimptotis.

3.4 Penerapan Kasus

3.4.1 Kasus I: Tanpa Vaksinasi

Pada bagian ini diberikan kasus tentang penyebaran penyakit yang diambil dari Makinde (2007). Diberikan laju infeksi = 0.8 sedangkan laju kesembuhan = 0.03. Besarnya laju kelahiran dan laju kematian penduduk adalah ȝ = 0.4. Kondisi awal rasio jumlah penduduk pada subpopulasi susceptible, infected, dan recovered masing-masing adalah 0.8, 0.2, dan 0.

Berdasarkan informasi tersebut, model dapat diekspresikan dari persamaan (3.1), (3.2), dan (3.3) menjadi:

. . .

. .

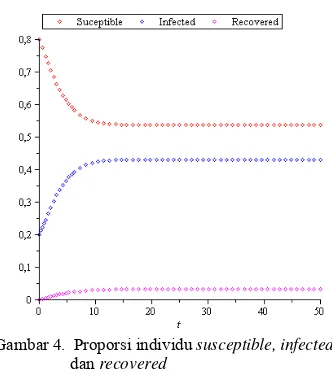
Proporsi susceptible, infected, dan recovered secara bersama disajikan pada Gambar 4.

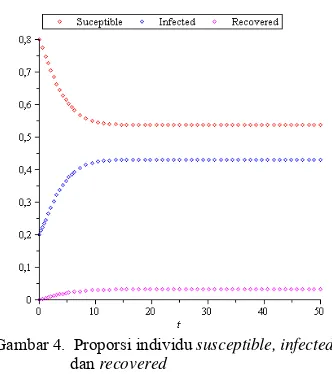
Gambar 4. Proporsi individu susceptible, infected,

dan recovered

Gambar 4 menunjukkan bahwa jumlah individu susceptible semakin berkurang sedangkan proporsi individu infected dan recovered mengalami kenaikan pada waktu awal . Hal ini terjadi karena individu

susceptible terinfeksi penyakit dan memasuki

subpopulasi infected kemudian individu infected yang sembuh dari penyakit memasuki subpopulasi recovered. Namun, pada waktu tertentu jumlah individu pada subpopulasi susceptible, infected, dan recovered tidak mengalami perubahan. Pada keadaan tersebut, sistem pada kondisi setimbang. Pada kondisi setimbang tersebut, penyakit akan selalu ada sampai waktu tak terbatas. Oleh karena itu, penyakit tersebut bersifat endemik. Kondisi setimbang tersebut dicapai saat:

, . , . .

Titik tersebut merupakan titik tetap endemik karena nilai .

Gambar tersebut juga menunjukkan bahwa pada kondisi setimbang, penyakit tidak akan menghilang untuk waktu ∞. Selanjutnya, akan ditentukan kestabilan dari titik tetap endemik . Besarnya bilangan reproduksi vaksinasi saat adalah . . Oleh karena itu, titik tetap endemik bersifat stabil asimptotis karena nilai memenuhi persamaan (3.19).

3.4.2 Kasus II: Dengan Vaksinasi

(10)

8

. . .

Vaksinasi dianggap berhasil jika pada waktu tertentu penyakit akan menghilang dari populasi. Bilangan reproduksi vaksinasi dapat digunakan untuk menentukan apakah penyakit tersebut akan menghilang dari populasi atau bersifat endemik. Penyakit akan menghilang dari populasi pada waktu tertentu jika sedangkan penyakit akan tetap ada sampai waktu tak terbatas (endemik) jika .

Sebagai upaya pencegahan penyebaran penyakit, dilakukan program vaksinasi pada tingkat . Dalam hal ini, dgunakan simulasi terhadap parameter tingkat vaksinasi untuk mengetahui pengaruh vaksinasi terhadap penyebaran penyakit. Pengaruh vaksinasi dapat dilihat pada perilaku proporsi individu

infected yang akan cenderung menghilang

atau bersifat endemik. Jika tingkat vaksinasi dilakukan antara . dan . maka proporsi individu infected disajikan pada Gambar 5.

Selanjutnya, tingkat vaksinasi dinaikkan lagi agar penyakit benar-benar menghilang dari populasi. Sebagai gambaran tentang upaya pencegahan penyebaran penyakit, diberikan parameter tingkat vaksinasi minimum yang diperlukan. Tingkat vaksinasi minimum yang diperlukan pada kasus ini adalah:

. .

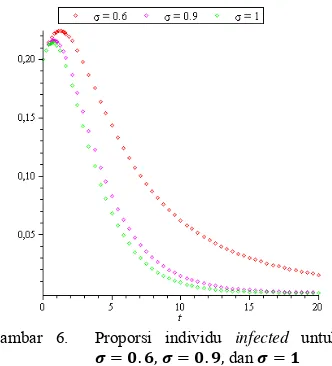
Jika dilakukan program vaksinasi pada tingkat , proporsi individu infected disajikan pula pada Gambar 5.

Gambar 5. Proporsi individu infected untuk . , . , dan

Gambar 5 menunjukkan bahwa penyakit akan selalu ada sampai waktu tak terbatas jika program vaksinasi yang dilakukan pada tingkat . sampai . . Oleh karena itu, penyakit bersifat endemik. Dengan demikian, vaksinasi yang dilakukan tidak berhasil membuat penyakit menghilang dari populasi. Akan tetapi penyakit dapat dimusnahkan dengan melakukan program vaksinasi pada tingkat . Namun, waktu yang diperlukan untuk memusnahkan penyakit tersebut sangat lama yaitu lebih dari 200 tahun. Oleh karena itu, program vaksinasi yang dilakukan belum cukup efektif untuk mencegah penyebaran penyakit

Gambar tersebut juga menunjukkan bahwa untuk , semakin tinggi tingkat vaksinasi mengakibatkan titik tetap endemik akan semakin menurun. Dengan demikian, pada titik tetap endemik, semakin tinggi tingkat vaksinasi mengakibatkan proporsi individu infected akan semakin menurun.

Berdasarkan persamaan yang diperoleh, tingkat vaksinasi yang dilakukan harus cukup lebih besar dari tingkat vaksinasi minimum agar penyebaran penyakit dapat dicegah dengan sukses.

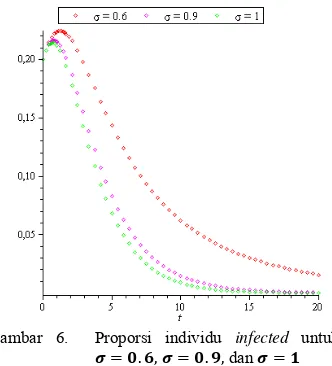
Selanjutnya, tingkat vaksinasi dilakukan pada tingkat . dan kemudian dinaikkan lagi untuk mengetahui pengaruh vaksinasi pada tingkat . maka proporsi individu infected disajikan pada Gambar 6.

Selanjutnya, jika setiap kelahiran memperoleh vaksin maka nilai . Jika

maka proporsi individu infected disajikan pula pada Gambar 6.

(11)

9

Sedangkan jika . penyakit akan menghilang dalam waktu kurang lebih 20 tahun. Dalam waktu kurang lebih 50 tahun, sistem akan setimbang saat:

, . ,

Titik tetap yang dimaksud adalah titik tetap bebas penyakit karena proporsi individu

infected bernilai nol. Besarnya bilangan

reproduksi vaksinasi adalah . . Titik tetap bebas penyakit tersebut bersifat stabil asimptotis karena .

Gambar tersebut juga menunjukkan bahwa penyakit akan menghilang dari populasi dalam waktu kurang lebih 18 tahun jika .

Titik tetap, bilangan reproduksi vaksinasi , dan kestabilan untuk , . ,

. , , . , . , dan disajikan pada Tabel 2.

Tabel 3. Titik tetap, bilangan reproduksi vaksinasi, dan kestabilan untuk , . ,

. , , . , . , dan

Titik Tetap Kestabilan 0 (0.5375,0.4302) 1.86 stabil

asimptotis 0.1 (0.5375,0.3372) 1.67 stabil

asimptotis (0.5375,0) 1 stabil 0.6 (0.4,0) 0.74 stabil

asimptotis 0.9 (0.1,0) 0.19 stabil

asimptotis

1 (0,0) 0 stabil

asimptotis

Tabel 3 menunjukkan bahwa semakin tinggi tingkat vaksinasi maka bilangan reproduksi vaksinasi akan semakin menurun. Penurunan tersebut menyebabkan proporsi individu infected pada titik tetap juga menurun. Tabel 3 juga menunjukkan bahwa untuk , kenaikan tingkat vaksinasi menyebabkan proporsi jumlah individu susceptible pada titik tetap akan menurun. Selanjutnya, untuk , pada titik tetap, proporsi individu susceptible bernilai nol. Hal ini menunjukkan bahwa semua individu telah kebal dari penyakit dan memasuki subpopulasi recovered. Titik tetap yang dicapai adalah titik tetap bebas penyakit karena nilai proporsi individu infected pada titik tersebut adalah nol.

Kriteria kestabilan di titik tetap dapat digambarkan dengan plot bidang fase

susceptible-infected. Sebagai contoh,

ditunjukkan kestabilan pada titik tetap untuk . . Titik tetap utuk . adalah titik tetap endemik:

. , .

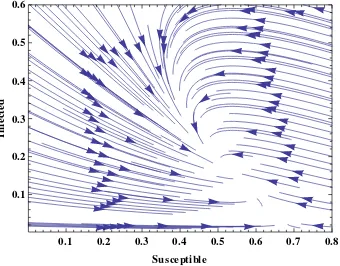
Plot bidang fase untuk . disajikan pada Gambar 7.

Gambar 7. Plot bidang fase untuk .

Gambar 7 menunjukkan bahwa semua plot bidang fase menuju ke arah titik tetap endemik. Oleh karena itu, titik tetap endemik tersebut bersifat stabil asimptotis.

Selanjutnya, akan ditunjukkan kestabilan pada titik tetap untuk . Titik tetap untuk

adalah titik tetap bebas penyakit: ,

Plot bidang fase untuk ditujukan pada Gambar 8.

Gambar 8. Plot bidang fase untuk

Gambar 8 menunjukkan bahwa semua plot bidang fase meuju ke arah titik tetap bebas penyakit. Oleh karena itu, titik tetap bebas penyakit bersifat stabil asimptotis.

Untuk mengamati pengaruh vaksinasi terhadap dinamika populasi individu rentan dan terinfeksi pada waktu tertentu maka diperlukan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi dengan variabel waktu. Hal ini membutuhkan

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.1 0.2 0.3 0.4 0.5 0.6 Susceptible In fe ct ed

(12)

10

nilai awal untuk semua parameter dan variabel.

Pada proses penggambarannya diambil nilai awal populasi individu yang rentan dan terinfeksi masing-masing adalah 80% dan 20%.

Pada bagian ini dianalisis dinamika populasi untuk dua kondisi yaitu perubahan parameter yang menunjukkan laju penularan penyakit dan perubahan parameter

yang menunjukkan laju kesembuhan dengan tingkat vaksinasi .

Proses penggambarannya dengan menggunakan Maple 13 yang dievaluasi ketika . , . , dan . dengan nilai awal . , . , dan

.

Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,

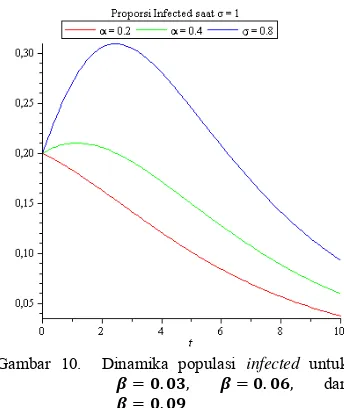
Gambar 9. Dinamika populasi infected untuk . , . ,dan .

Gambar 9 menunjukkan hubungan populasi infected terhadap waktu t. Kurva di atas dibandingkan berdasarkan nilai yang berbeda yaitu . , . , dan . . Dari kurva di atas dapat dilihat bahwa individu rentan dan yang terinfeksi mengalami penurunan terus menuju nol yang artinya menuju kepunahan. Semakin besar nilai , pada awal kurva tersebut semakin ke atas, artinya laju penularan penyakit ketika . lebih besar dari laju penularan penyakit ketika

. dan laju penularan penyakit ketika . lebih besar dari laju penularan penyakit ketika . dan . . Ini berarti bahwa ketika laju penularan penyakit meningkat mengakibatkan banyaknya individu yang terinfeksi juga meningkat.

Gambar 10. Dinamika populasi infected untuk

. , . , dan

.

Gambar 10 menunjukkan hubungan populasi infected terhadap waktu t. Kurva di atas dibandingkan berdasarkan nilai yang berbeda yaitu . , . , dan . . Dari kurva di atas dapat dilihat bahwa individu rentan dan yang terinfeksi mengalami penurunan terus menuju nol yang artinya menuju kepunahan. Semakin besar nilai , pada awal kurva tersebut semakin ke bawah, artinya laju kesembuhan penyakit ketika

(13)

IV.

SIMPULAN

Dalam karya tulisi ini dianalisis pengaruh vaksinasi terhadap model epidemik SIR. Sebagai hasil analisis kesetimbangan model ini diperoleh dua titik tetap, yaitu titik tetap bebas penyakit dan titik tetap endemik. Analisis kestabilan titik tetap bebas penyakit dan titik tetap endemik masing-masing bersifat tidak stabil dan stabil asimptotis.

Pada penerapan kasus, model SIR tersebut dibedakan menjadi dua macam yaitu dengan dipengaruhi vaksinasi dan tanpa dipengaruhi vaksinasi. Pengaruh tingkat vaksinasi pada penyebaran penyakit untuk tingkat vaksinasi di bawah ambang vaksinasi, semakin besar tingkat vaksinasi akan menyebabkan proporsi individu infected pada titik tetap semakin

kecil. Untuk tingkat vaksinasi di atas ambang vaksinasi, semakin besar tingkat vaksinasi menyebabkan proporsi individu susceptible pada titik tetap semakin kecil dan penyakit akan menghilang dari populasi dalam waktu yang lebih cepat. Pengaruh vaksinasi terhadap dinamika individu rentan dan yang terinfeksi yaitu ketika laju penularan penyakit meningkat mengakibatkan banyaknya individu yang terinfeksi juga meningkat. Selanjutnya, ketika laju kesembuhan penyakit meningkat mengakibatkan banyaknya individu yang terinfeksi menurun.

DAFTAR PUSTAKA

Bellomo N. and Preziosi L. 1995. Mathematical Modeling. CRC Press, Florida.

Farlow SJ. 1994. An Introduction to Differential Equation and Their Application. Mc Graw-Hill, New York. Giesecke J. 1994. Modern Infectious Disease

Epidemiology. Oxford University Press, New York.

Hethcote HW. 2000. The Mathematics of Infectious Diseases. SIAM Review. no. 4. pp. 599-653.

Makinde OD. 2007. Adomian Decomposition Approach to a SIR Epidemic Model with Constant Vaccination Strategy. Comput. Appl. Math. 184. pp. 842-848.

Strogatz SH. 1994. Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. Addison-Wesley Publishing Company, Reading, Massachusete.

Tu PNV. 1994. Dynamical System, An Introduction with Application in Economics and Biology. Springer-Verlag. Heidelberg, Germany.

UNICEF. 2007. Polio: Stories from West

Java. http: // www.unicef.org

/indonesia/reallives_2956.html di akses pada tanggal 12 September 2010.

WHO. 2007. Measles. http: // www.who.int /mediacentre/factsheets/fs286/en/ di akses pada tanggal 12 September

(14)

PENGARUH VAKSINASI TERHADAP DINAMIKA POPULASI

PADA MODEL

SIR (Susceptible-Infected-Recovered)

SUBRO MULISI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(15)

PENGARUH VAKSINASI TERHADAP DINAMIKA POPULASI

PADA MODEL

SUBRO MULISI

INSTITUT PERTANIAN BOGOR

(16)

ABSTRAK

SUBRO MULISI. Pengaruh Vaksinasi terhadap Dinamika Populasi pada Model SIR (Susceptible-Infected-Recovered). Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan ALI KUSNANTO.

Model SIR digunakan untuk memodelkan penyebaran suatu penyakit dalam suatu populasi tertutup berdasarkan asumsi-asumsi tertentu. Pada penelitian ini, model SIR dirumuskan dengan memasukkan faktor vaksinasi. Dari hasil analisis model, dihasilkan dua titik kesetimbangan yaitu titik kesetimbangan bebas penyakit dan titik kesetimbangan endemik.

(17)

ABSTRACT

SUBRO MULISI. The Effect of Vaccination in Population Dynamics with SIR

(Susceptible-Infected-Recovered) Model. Supervised by ENDAR HASAFAH NUGRAHANI and ALI

KUSNANTO.

SIR model can be used to model the spread of diseases in a closed population based on certain assumptions. In this research, the SIR model is formulated by including the factor of vaccination. As the result, the model has been shown to have two equilibrium points, i.e. disease free and endemic equilibrium.

(18)

PENGARUH VAKSINASI TERHADAP DINAMIKA POPULASI

PADA MODEL

SUBRO MULISI

G54063144

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

INSTITUT PERTANIAN BOGOR

(19)

Judul

: Pengaruh Vaksinasi terhadap Dinamika Populasi pada Model

SIR

(Susceptible-Infected-Recovered)

Nama

: Subro Mulisi

NIM :

G54063144

Menyetujui

Pembimbing

1

Pembimbing

II

Dr. Ir. Endar Hasafah Nugrahani, MS

Drs. Ali Kusnanto, M.Si

NIP. 19631228 198903 2 001

NIP. 19650820 199003 1 001

Mengetahui

Ketua Departemen Matematika

Dr. Berlian Setiawaty, MS

NIP. 19650505 198903 2 004

(20)

KATA PENGANTAR

Alhamdulillahirobbil’alamin. Penulis mengucapkan syukur kehadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini tidak terlepas dari dukungan dan bantuan dari berbagai pihak. Pada kesempatan ini, penulis juga ingin mengucapkan terimakasih yang sebesar-besarnya kepada: 1. Mamo dan Emak tersayang, terima kasih atas didikan, kasih sayang, nasihat, semangat, serta

do’a yang tiada henti-hentinya. Do’a yang selalu menjadi penerang jalan penulis.

2. Dr. Ir. Endar Hasafah Nugrahani, MS. selaku dosen pembimbing I, Drs. Ali Kusnanto, M.Si. selaku pembimbing II. Terimakasih atas waktu, ilmu yang diberikan dan kesabarannya dalam membimbing penulis. Semua ilmu yang Bu Endar dan Pak Ali berikan sangat bermanfaat bagi penulis. Terima kasih.

3. Ir. N. K. Kutha Ardana, M.Sc. selaku dosen penguji. Terimakasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis.

4. Kakak-kakakku tersayang (Asmaiyah, Rahmatullah, Heriyah, Abdurahman, dan Ahmad Aziz), kakak ipar (Dadang, Ihat, Dendi, dan Ayu), terimakasih atas do’a, semangat dan dukungannya.

5. Keponakanku (Aqlus, Nissa, Faruq, Zahra, Mujib, Zaki, Aufa, Rara, Intan, dan Vanes), terima kasih atas keceriaan dan senyum manis yang selalu hadir pada wajah mungil kalian. 6. Semua dosen Departemen Matematika, terimakasih atas ilmu yang telah diberikan.

7. Pak Yono, Bu Ade, Bu Susi, Mas Bono, Mas Heri, Mas Deni dan seluruh staf pegawai Departemen Matematika, terimakasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di Departemen Matematika.

8. Sahabat – sahabat laskar Jumat Kliwon: Imam Kamarudin Saleh, Oyok Sopian, Lilis Sucahyo, Pandu Mas Saputra, Deni Saputra, Deni Hamdan, Shiddiq Ardi Kurniawan.

9. Pada para asatidz: Ust. Hajarul Aswad, Ust Aji Ashari, Ust. Ihsan, Ust. Hasyim.

10. Guru-guru SMA Negeri 1 Cilegon (Pak Arudin, Bu Oom, dan lain-lain), SLTP Negeri 5 Cilegon, dan SD Negeri VI Cilegon. Tanpamu, penulis takkan berdiri di sini. Terima Kasih. 11. Teman-teman satu bimbingan yang sudah lulus terlebih dahulu: Rias, Nene, dan Ria. Terima

kasih atas doa, bantuan, dukungan semangat, dan nasehatnya.

12. Kakak kelas angkatan 41 dan 42 yang tidak bisa penulis sebutkan satu per satu.

13. Teman-teman angkatan 43: Ria, Margi, Suci, Aini, Nene, Putri, Lina, Lia, Erni, Rias, Arum, Nia, Destya, Resti, Nidya, Tami, Maria Herlina, Narsih, Desy, Ratna Agung, Cici, Vera, Rizki SN, Rizki NS, Kiki, Apri, Ace, Mamet, Supri, Irsyad, Copi, Wira, Peli, Arif, Mubarok, Ryan, Fardan, Nanu, Dwi, David, Adi, Ecka, Sendy, Dandi, Zul, Adam, Kunto, Syahrul, Faisol, Elly, Hendra, Razon, Kabil, Sabar, Gandi, Emta, Andrew, Ucok, dan Nobo. Terimakasih atas doa, dukungan dan semangatnya, terimakasih atas kebersamaannya selama 3 tahun di Math’43.

14. Adik kelas angkatan 44, 45 dan 46 yang tidak bisa penulis sebutkan satu per satu.

15. Teman-temanku di Rumah Senyum dan Batu: Aden, Izan, Andra dan lainnya yang tidak bisa ditulis satu per satu, terimakasih atas doa, bantuan, dan dukungan semangatnya.

Penulis menyadari tulisan ini masih memiliki kekurangan dan jauh dari kesempurnaan. Oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.

Semoga karya ilmiah ini bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan khususnya Matematika.

Bogor, Januari 2011

(21)

RIWAYAT HIDUP

Penulis lahir di Serang, Banten pada tanggal 7 Mei 1988 sebagai anak ke enam dari enam bersaudara, anak dari pasangan H. Yusi Tu’ab dan Masitah. Tahun 2000 penulis lulus dari SDN VI Cilegon. Tahun 2003 penulis lulus dari SLTPN 5 Cilegon. Tahun 2006 penulis lulus dari SMAN 1 Cilegon dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Seleksi Penerimaan Mahasiswa Baru (SPMB), Tingkat Persiapan Bersama. Pada tahun 2007, penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

(22)

DAFTAR ISI

Halaman

DAFTAR ISI ... vii DAFTAR GAMBAR ...viii DAFTAR TABEL ...viii DAFTAR LAMPIRAN ...viii

I PENDAHULUAN

1.1 Latar Belakang ... 1 1.2 Tujuan Penulisan ... 1 1.3 Sistematika Penulisan ... 1 II LANDASAN TEORI

2.1 Sistem Persamaan Diferensial Mandiri ... 2 2.2 Titik Tetap ... 2 2.3 Pelinearan ... 2 2.4 Nilai Eigen dan Vektor Eigen ... 2 2.5 Kestabilan Titik Tetap ... 2 2.6 Bilangan Reproduksi Dasar ... 3 III PEMBAHASAN

3.1 Konstruksi Model ... 4 3.2 Kesetimbangan Model ... 5 3.3 Analisis Kestabilan Titik Tetap ... 5 3.4 Penerapan Kasus ... 7

IV SIMPULAN ... 11

DAFTAR PUSTAKA ... 11

LAMPIRAN ... 12

(23)

DAFTAR GAMBAR

1 Jenis-jenis kestabilan titik tetap ... 3 2 Model SIR ... 4 3 Dinamika populasi model SIR dengan pengaruh vaksinasi ... 5 4 Proporsi individu susceptible, infected, dan recovered ... 7 5 Proporsi individu infected untuk . , . , dan ... 8 6 Proporsi individu infected untuk . , . , dan ... 8 7 Plot bidang fase untuk . ... 9 8 Plot bidang fase untuk ... 9 9 Dinamika populasi infected untuk . , . , dan . ... 10 10 Dinamika populasi infected untuk . , . , dan . ... 10

DAFTAR TABEL

1 Kriteria kestabilan berdasarkan nilai eigen ... 3 2 Kondisi kestabilan titik tetap ... 7 3 Titik tetap, bilangan reproduksi vaksinasi, dan kestabilan ... 9

DAFTAR LAMPIRAN

1 Pencarian Titik Tetap Sistem Persamaan (3.8) ... 13 2 Matriks Jacobi dan Nilai Eigen untuk Titik Tetap (Persamaan (3.7)) ... 13 3 Pencarian ... 14 4 Simulasi Bidang Solusi Susceptible-Infected-Recovered pada Kasus I ... 14 5 Simulasi Bidang Solusi dan Bidang Fase Susceptible-Infected pada Kasus II ... 14

(24)

I.

PENDAHULUAN

1.1 Latar Belakang

Model matematika merupakan salah satu alat yang dapat membantu mempermudah penyelesaian masalah dalam kehidupan nyata. Masalah-masalah tersebut dapat dibawa ke dalam model matematis dengan menggunakan asumsi-asumsi tertentu. Selanjutnya, dari model yang didapat akan dicari solusinya, baik dengan cara analitis maupun secara numerik.

Salah satu permasalahan pada kehidupan nyata adalah mengenai penyebaran suatu penyakit, di mana individu yang terinfeksi akan mempunyai kekebalan dalam jangka waktu tertentu, contohnya adalah penyakit campak dan influenza. Penyakit measles (campak), mumps (gondong), rubella (campak Jerman), dan poliomyelitis (polio) merupakan penyakit infeksi yang sangat berbahaya. Penyakit tersebut disebabkan oleh virus yang dapat menyebar melalui kontak langsung dengan penderita, udara batuk atau bersin, dan kotoran manusia. Anak-anak yang biasanya lebih sering terjangkit penyakit tersebut. Oleh karena itu, salah satu upaya yang dilakukan UNICEF untuk mencegah meluasnya penyakit tersebut adalah dengan melakukan program vaksinasi (UNICEF 2007).

Perkembangan ilmu pengetahuan di bidang matematika juga turut memberikan peranan yang penting dalam mencegah meluasnya penyebaran penyakit tersebut. Peranan tersebut berupa penyelesaian masalah tentang penyebaran penyakit. Selanjutnya, masalah penyebaran penyakit ini akan dimodelkan secara matematis menggunakan tipe model penyebaran penyakit SIR (Suspected-Infected-Recovered). Secara umum model epidemi SIR ini dapat disajikan sebagai sistem persamaan diferensial autonomous/mandiri. Sistem persamaan diferensial mandiri epidemi SIR ini secara garis besar menggambarkan alur penyebaran penyebaran penyakit dari subpopulasi individu susceptible (rentan) menjadi infected (terinfeksi) melalui kontak langsung maupun perantara lain. Selanjutnya individu infected yang mampu bertahan terhadap penyakit akan sembuh dan memasuki subpopulasi recovered (sembuh).

Model SIR selanjutnya digunakan untuk memodelkan penyebaran penyakit yang bersifat endemik. Berdasarkan data dari

WHO, penyebaran penyakit dapat ditekan setelah adanya program vaksinasi (WHO 2007). Sampai saat ini, program vaksinasi masih dipercaya sebagai cara yang paling efektif dalam menekan penyebaran penyakit. Oleh karena itu, vaksinasi harus diperhatikan dalam model sebagai upaya untuk mencegah meluasnya penyakit.

Mobilitas atau perpindahan populasi dari suatu wilayah ke wilayah lain dapat terjadi dalam suatu wilayah. Mobilitas tersebut secara umum disebut sebagai migrasi. Adanya migrasi dapat memungkinkan terjadinya penyebaran penyakit yang dibawa oleh populasi yang masuk atau keluar dari suatu wilayah. Oleh karena itu, pengaruh migrasi perlu diperhatikan dalam model. Namun, dalam populasi tertutup, migrasi tidak terjadi dalam wilayah tersebut sehingga tidak diperhatikan dalam model.

Pada karya ilmiah ini, akan dianalisis sebuah model SIR yang dikembangkan oleh Kermack dan McKendrick (Makinde 2007). Model tersebut akan dipengaruhi faktor adanya vaksinasi dengan tingkatan yang tinggi atau rendah serta faktor tidak adanya vaksinasi yang akan ditentukan kestabilan di titik tetapnya.

1.2 Tujuan Penulisan

Tujuan dari penulisan karya ilmiah ini adalah untuk merumuskan model SIR dengan pengaruh vaksinasi serta pengaruhnya terhadap dinamika populasi dan melakukan simulasi terhadap nilai-nilai parameter yang mempengaruhinya.

1.3 Sistematika Penulisan

(25)

II.

LANDASAN TEORI

2.1 Sistem Persamaan Diferensial Mandiri

Perhatikan sistem persamaan diferensial (SPD) berikut:

,

(2.1)

,

dan adalah fungsi kontinu dari dan dengan turunan parsial pertama kontinu, dengan laju perubahan dan dinyatakan dengan fungsi eksplisit dari dan sendiri dan tidak mengandung . SPD (2.1) disebut sebagai sistem persamaan diferensial autonomous/mandiri.

[Farlow 1994]

2.2 Titik Tetap

Misalkan diberikan persamaan diferensial (SPD) sebagai berikut:

, . Titik disebut titik tetap jika memenuhi

. Titik tetap disebut juga titik kritis atau titik kesetimbangan. Untuk selanjutnya akan digunakan istilah titik tetap.

[Tu 1994]

2.3 Pelinearan

Misalkan:

, ,

Andaikan , adalah titik tetap dari persamaan di atas, maka , dan

, . Misalkan dan

maka didapatkan: , , , , , , , , , , , ,

Dalam bentuk matriks:

, ,

Matriks

,

disebut

matriks Jacobi pada titik tetap , . Karena , , maka dapat diabaikan sehingga didapat persamaan linear:

.

[Strogatz 1994]

2.4 Nilai Eigen dan Vektor Eigen

Misalkan matriks berukuran . Suatu vektor tak nol di disebut vektor eigen dari jika untuk suatu skalar, yang disebut nilai eigen dari berlaku:

. Vektor disebut vektor eigen yang bersesuaian dengan nilai eigen .

Untuk mencari nilai eigen dari matriks yang berukuran , maka persamaan (2.4) dapat ditulis sebagai berikut:

. Dengan adalah matriks identitas berukuran . Persamaan (2.5) mempunyai solusi tak nol jika dan hanya jika:

. Persamaan (2.6) disebut persamaan karakteristik dari .

[Tu 1994]

2.5 Kestabilan Titik Tetap

Diberikan sistem persamaan differensial sembarang:

, . Analisis kestabilan titik tetap dilakukan melalui matriks Jacobi, yaitu matriks . Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigennya, yaitu dengan , , , … yang diperoleh dari

(26)

Secara umum kestabilan titik tetap mempunyai tiga perilaku sebagai berikut: 1. Stabil, jika

a. Setiap nilai eigen real adalah negatif ( untuk semua )

b. Setiap komponen bagian real dari nilai eigen kompleks, lebih kecil atau sama dengan nol ( untuk semua ).

2. Takstabil, jika

a. Ada nilai eigen real yang positif ( untuk suatu ).

b. Ada komponen bagian real dari nilai eigen kompleks, lebih besar dari nol ( untuk suatu ).

3. Sadel, jika perkalian dua buah nilai eigen real sembarang adalah negatif ( , untuk dan sembarang). Titik tetap sadel ini bersifat takstabil.

[Tu 1994]

2.6 Bilangan Reproduksi Dasar

Bilangan reproduksi dasar adalah rata-rata banyaknya individu yang rentan terinfeksi secara langsung oleh individu lain yang telah terinfeksi bila individu yang telah terinfeksi tersebut masuk ke dalam populasi yang seluruhnya masih rentan. Bilangan reproduksi dasar dilambangkan dengan .

Beberapa kondisi yang akan timbul, yaitu 1. Jika , maka penyakit akan

menghilang.

2. Jika , maka penyakit akan menetap.

3. Jika , maka penyakit akan meningkat menjadi wabah.

[Giesecke 1994]

Pada Tabel 1 berikut diberikan tabel jenis-jenis kestabilan titik tetap berdasarkan nilai eigennya serta pada Gambar 1 diberikan juga gambar jenis-jenis kestabilan titik tetap [Bellomo & Preziosi 1995]:

Tabel 1. Kriteria kestabilan berdasarkan nilai eigen

Nilai eigen Nama Kestabilan

real, tidak sama, bertanda sama

simpul stabil asimptotis: semuanya negatif tidak stabil: semuanya positif real, tidak sama,

berlawanan tanda

sadel tidak stabil

real, sama simpul stabil asimptotis: semuanya negatif tidak stabil: semuanya positif kompleks konjugate

bukan imajiner murni

spiral stabil asimptotis: bagian real negatif tidak stabil: bagian real positif imajiner mutni pusat stabil

Gambar 1. Jenis-jenis kestabilan titik tetap

Simpul stabil Simpul tak stabil

Titik pusat Titik sadle

Spiral stabil _{Spiral tak stabil}

(27)

III.

PEMBAHASAN

3.1 Konstruksi Model

3.1.1 Model SIR

Model SIR yang digunakan dalam tulisan ini disusun oleh Kermack and McKendrick. Model SIR (Susceptibles, Invectives, Recovered) pada awalnya dikembangkan untuk mengetahui laju penyebaran dan kepunahan suatu wabah penyakit dalam populasi tertutup dan bersifat epidemik (Makinde 2007). Pada tulisan ini dibahas mengenai pembentukan model SIR berdasarkan asumsi yang dibuat. Setelah model terbentuk, kemudian dicari solusi analitis dan titik tetapnya, yang selanjutnya diinterpretasikan dalam permasalahan yang sesungguhnya dalam kehidupan nyata. Dalam hal ini adalah mengenai perilaku penyebaran penyakit dan eksistensinya, yaitu titik tetap bebas penyakit dan titik tetap endemik.

Penyebaran penyakit dalam suatu populasi diasumsikan memiliki jumlah konstan dan dalam satu periode waktu wabah. Pada saat t misalkan suatu populasi terdiri dari:

Susceptibles S(t): adalah subpopulasi di

mana anggotanya terdiri dari orang-orang yang rentan terkena penyakit tersebut.

InfectivesI(t): adalah subpopulasi di mana anggotanya terdiri dari orang-orang yang sudah terjangkit penyakit tersebut.

RecoveredR(t): adalah subpopulasi yang

telah sembuh dari penyakit tersebut. Dengan proporsi

Pada pembentukan model SIR diberikan berbagai asumsi yang terdiri dari:

1) Populasi tertutup (tidak ada proses migrasi).

2) Terjadi proses kelahiran dan kematian.

3) Laju kelahiran sama dengan laju kematian (jumlah populasi tetap). 4) Penyakit dapat disembuhkan.

5) Setiap individu yang belum terserang penyakit masuk ke subpopulasi susceptibles (rentan terserang). 6) Individu yang sembuh mempunyai

kekebalan tetap.

7) Penyakit menular melalui kontak langsung antara individu rentan dengan penderita.

8) Tidak ada masa inkubasi apabila terjadi proses penularan.

9) Masa terjangkit yang cukup lama.

Diasumsikan terdapat kontak yang tetap dari subpopulasi S dan I dalam populasi tersebut dan angka susceptible S(t) ditambah dengan bilangan konstan ȝ. Bilangan konstan

ȝ melambangkan kondisi di mana muncul kelahiran baru dan bayi yang baru lahir otomatis masuk dalam kondisi rentan. Karena laju kelahiran sama dengan laju kematian, maka nilai kedua laju sama yaitu ȝ. Misalkan laju penularan penyakit adalah , maka dalam satu waktu laju dari susceptibles menjadi infective adalah:

. dengan dan ȝ adalah konstan positif dan ȝS adalah jumlah kematian pada subpopulasi S. Jika > 0 adalah laju kesembuhan dari

infected menjadi recovered, maka:

. dengan ȝI adalah jumlah kematian pada subpopulasi I, dan laju perubahan subpopulasi recovered menjadi:

. dengan ȝR adalah jumlah kematian dari subpopulasi R.

Gambar 2. Model SIR

3.1.2 Model SIR dengan Pengaruh Vaksinasi

Selanjutnya, program vaksinasi diperhatikan dalam model (Makinde 2007). Dalam hal ini, vaksin hanya diberikan pada individu yang baru lahir atau masih dalam usia anak-anak. Diasumsikan bahwa efisiensi vaksinasi adalah 100% yang berarti setiap individu yang telah mendapat vaksin akan kebal dari penyakit. Kekebalan yang terjadi karena vaksin bersifat permanen yang berarti individu tersebut tidak dapat terinfeksi oleh penyakit yang dimaksud.

Diasumsikan rasio jumlah individu yang memperoleh vaksin adalah . Individu yang memperoleh vaksin akan kebal dari penyakit dan memasuki subpopulasi R. Jumlah individu yang memperoleh vaksin proporsional dengan jumlah kelahiran . Dengan demikian, jumlah

(28)

individu yang kebal dari penyakit karena telah memperoleh vaksin adalah .

Jumlah individu yang tidak mendapat

vaksin adalah .

Selanjutnya individu yang tidak mendapatkan vaksin akan memasuki subpopulasi S dan berpotensi untuk terinfeksi penyakit.

Alur perpindahan individu susceptible menjadi infected kemudian sembuh dan memasuki subpopulasi recovered disajikan pada Gambar 3.2. Nilai parameter dari , , dan adalah positif. Batas dari laju vaksinasi adalah .

Laju perubahan individu pada subpopulasi S dapat diekspresikan sebagai:

.

Gambar 3. Dinamika populasi model SIR dengan pengaruh vaksinasi

Laju perubahan individu pada subpopulasi I dapat dinyatakan sebagai:

. Laju perubahan individu pada subpopulasi R adalah:

.

dengan , , dan .

3.2 Kesetimbangan Model

Pada persamaan (3.4) dan (3.5) variabel R tidak muncul. Hal ini menunjukkan bahwa jumlah individu pada subpopulasi R tidak mempengaruhi laju perubahan jumlah individu pada subpopulasi S maupun I. Dari

proporsi , didapat

sehingga penyelesaian untuk R dapat diperoleh dengan

mudah jika penyelesaian untuk S dan I sudah diperoleh. Dengan demikian, berdasarkan kondisi tersebut, persamaan (3.4), (3.5), dan (3.6) dapat diperhatikan sebagai:

(3.7)

Titik tetap persamaan (3.7) dapat diperoleh dengan menentukan:

(3.8)

Dari persamaan (3.8) di atas diperoleh dua titik tetap:

1. Titik tetap yang pertama diekspresikan sebagai:

,

Nilai I = 0 berarti tidak ada individu pada kelompok I yang dapat menyebabkan penyakit. Titik tetap ini juga dapat dituliskan dengan

, .

2. Titik tetap yang kedua diekspresikan sebagai:

, (bukti lihat Lampiran 1).

Titik tetap ini bisa dituliskan sebagai , , nilai yang tidak nol menunjukkan bahwa terdapat individu pada kelompok I yang dapat menyebarluaskan penyakit dan menyebabkan endemik.

3.3 Analisis Kestabilan Titik Tetap

Analisis kestabilan ditentukan berdasarkan nilai eigen dari matriks Jacobian yang diperoleh dari metode linearisasi. Matriks Jacobian yang diperoleh dari persamaan (3.7) adalah:

. Kestabilan dari titik-titik tetap dan ditentukan berdasarkan nilai eigen dan matriks Jacobian di titik-titik tersebut.

3.3.1 Kestabilan di Titik Tetap

. (bukti lihat Lampiran 2)

dengan S σ . Nilai eigen dari matriks Jacobian (3.10) diperoleh dengan menggunakan persamaan karakteristik | Ι| yaitu:

dan

E0 akan bersifat stabil asimptotis jika untuk i = 1, 2. Nilai mengakibatkan nilai . Jika

maka mengakibatkan:

S I R

Vaksin

(29)

. di mana merupakan bilangan reproduksi

vaksinasi , sehingga titik akan bersifat stabil asimptotis untuk . Namun, jika

maka titik akan tidak stabil.

3.3.2 Bilangan Reproduksi Vaksinasi

Untuk mengetahui tingkat penyebaran suatu penyakit diperlukan suatu parameter tertentu. Parameter yang biasa digunakan dalam masalah penyebaran penyakit adalah bilangan reproduksi vaksinasi. Menurut Hethcote (2000), bilangan reproduksi merupakan bilangan yang menunjukkan jumlah individu susceptible yang dapat menderita penyakit yang diakibatkan oleh satu individu infected. Bilangan reproduksi selanjutnya merupakan bilangan reproduksi pada kasus yang memperhatikan faktor vaksinasi.

Berdasarkan titik tetapnya, bilangan reproduksi vaksinasi dapat diekspresikan sebagai:

. (bukti lihat Lampiran 3).

Jika maka untuk ∞, yang berarti bahwa jumlah penderita penyakit berangsur-angsur semakin berkurang sehingga penyakit akan menghilang dari populasi dan tidak terjadi endemik. Jika maka

, yang berarti jumlah penderita penyakit berangsur-angsur semakin bertambah sehingga penyakit akan meluas dan menjadi endemik.

Berdasarkan definisi titik tetap, nilai pada persamaan (3.12) didekati dengan titik tetap bebas penyakit yaitu . Sehingga nilai

dapat diekspresikan dengan:

. Dari persamaan (3.13) dapat didefinisikan tingkat vaksinasi minimum yang diperlukan untuk mencegah menyebarnya penyakit. Tingkat vaksinasi merupakan proporsi kelahiran yang mendapatkan vaksin. Tingkat vaksinasi minimum yang diperlukan untuk mencegah menyebarnya penyakit dinotasikan dengan . Penyakit akan berangsur-angsur menghilang dari populasi untuk . Dengan demikian, untuk diperoleh tingkat vaksinasi minimum yaitu:

Dari persamaan yang diperoleh di atas, tingkat vaksinasi yang diberikan harus lebih besar dari agar penyakit dapat dicegah penyebarannya. Jika tingkat vaksinasi yang diberikan lebih besar dari tingkat vaksinasi minimum maka:

(3.14)

Persamaan (3.14) mengakibatkan bahwa jumlah individu susceptible yang dapat terinfeksi penyakit yang diakibatkan oleh satu individu infected dengan tingkat pemberian vaksinasi akan lebih kecil jika dibandingkan saat diberikan vaksin pada tingkat . Oleh karena itu, tingkat vaksinasi yang diberikan harus lebih besar dari agar jumlah penderita dapat ditekan sekecil mungkin dan penyakit dapat menghilang dari populasi.

Selanjutnya, jika tingkat vaksinasi maka:

(3.15)

Persamaan (3.15) menyebabkan penyakit akan menjadi endemik jika tingkat vaksinasi yang diberikan lebih kecil dari tingkat vaksinasi minimum .

3.3.3 Kestabilan di Titik Tetap

. Karena titik tetap :

,

matriks Jacobian pada persamaan (3.16) menjadi:

. Titik tetap diekspresikan menggunakan definisi bilangan produksi vaksinasi menjadi:

(30)

7

, , .

Dengan menggunakan persamaan (3.18), diperoleh nilai eigen dari matriks Jacobian (3.17) yaitu:

,

(bukti lihat Lampiran 2).

Dari persamaan (3.18), titik endemik hanya akan muncul jika sedangkan nilai eigen Ȝ1,2 akan berupa bilangan real negatif atau bilangan kompleks dengan bagian real bernilai negatif untuk:

. Kondisi (3.19) menyebabkan titik tetap Ee akan bersifat stabil asimptotis.

Berikut adalah tabel kondisi kestabilan dari kedua titik tetap yang diperoleh.

Tabel 2. Kondisi kestabilan titik tetap Kondisi Stabil asimptotis Tidak stabil Tidak stabil Stabil asimptotis

Dari Tabel 2 dapat dilihat bahwa kondisi kestabilan dari titik tetap yang diperoleh saling berbeda. Ketika titik tetap yang pertama stabil asimptotis, titik tetap yang kedua tidak stabil dan ketika titik tetap yang pertama tidak stabil, titik tetap yang kedua stabil asimptotis.

3.4 Penerapan Kasus

3.4.1 Kasus I: Tanpa Vaksinasi

Pada bagian ini diberikan kasus tentang penyebaran penyakit yang diambil dari Makinde (2007). Diberikan laju infeksi = 0.8 sedangkan laju kesembuhan = 0.03. Besarnya laju kelahiran dan laju kematian penduduk adalah ȝ = 0.4. Kondisi awal rasio jumlah penduduk pada subpopulasi susceptible, infected, dan recovered masing-masing adalah 0.8, 0.2, dan 0.

Berdasarkan informasi tersebut, model dapat diekspresikan dari persamaan (3.1), (3.2), dan (3.3) menjadi:

. . .

. .

[image:30.612.335.501.108.295.2]

Proporsi susceptible, infected, dan recovered secara bersama disajikan pada Gambar 4.

Gambar 4. Proporsi individu susceptible, infected,

dan recovered

Gambar 4 menunjukkan bahwa jumlah individu susceptible semakin berkurang sedangkan proporsi individu infected dan recovered mengalami kenaikan pada waktu awal . Hal ini terjadi karena individu

susceptible terinfeksi penyakit dan memasuki

subpopulasi infected kemudian individu infected yang sembuh dari penyakit memasuki subpopulasi recovered. Namun, pada waktu tertentu jumlah individu pada subpopulasi susceptible, infected, dan recovered tidak mengalami perubahan. Pada keadaan tersebut, sistem pada kondisi setimbang. Pada kondisi setimbang tersebut, penyakit akan selalu ada sampai waktu tak terbatas. Oleh karena itu, penyakit tersebut bersifat endemik. Kondisi setimbang tersebut dicapai saat:

, . , . .

Titik tersebut merupakan titik tetap endemik karena nilai .

Gambar tersebut juga menunjukkan bahwa pada kondisi setimbang, penyakit tidak akan menghilang untuk waktu ∞. Selanjutnya, akan ditentukan kestabilan dari titik tetap endemik . Besarnya bilangan reproduksi vaksinasi saat adalah . . Oleh karena itu, titik tetap endemik bersifat stabil asimptotis karena nilai memenuhi persamaan (3.19).

3.4.2 Kasus II: Dengan Vaksinasi

(31)

8

. . .

Vaksinasi dianggap berhasil jika pada waktu tertentu penyakit akan menghilang dari populasi. Bilangan reproduksi vaksinasi dapat digunakan untuk menentukan apakah penyakit tersebut akan menghilang dari populasi atau bersifat endemik. Penyakit akan menghilang dari populasi pada waktu tertentu jika sedangkan penyakit akan tetap ada sampai waktu tak terbatas (endemik) jika .

Sebagai upaya pencegahan penyebaran penyakit, dilakukan program vaksinasi pada tingkat . Dalam hal ini, dgunakan simulasi terhadap parameter tingkat vaksinasi untuk mengetahui pengaruh vaksinasi terhadap penyebaran penyakit. Pengaruh vaksinasi dapat dilihat pada perilaku proporsi individu

infected yang akan cenderung menghilang

atau bersifat endemik. Jika tingkat vaksinasi dilakukan antara . dan . maka proporsi individu infected disajikan pada Gambar 5.

Selanjutnya, tingkat vaksinasi dinaikkan lagi agar penyakit benar-benar menghilang dari populasi. Sebagai gambaran tentang upaya pencegahan penyebaran penyakit, diberikan parameter tingkat vaksinasi minimum yang diperlukan. Tingkat vaksinasi minimum yang diperlukan pada kasus ini adalah:

. .

Jika dilakukan program vaksinasi pada tingkat , proporsi individu infected disajikan pula pada Gambar 5.

Gambar 5 menunjukkan bahwa penyakit akan selalu ada sampai waktu tak terbatas jika program vaksinasi yang dilakukan pada tingkat . sampai . . Oleh karena itu, penyakit bersifat endemik. Dengan demikian, vaksinasi yang dilakukan tidak berhasil membuat penyakit menghilang dari populasi. Akan tetapi penyakit dapat dimusnahkan dengan melakukan program vaksinasi pada tingkat . Namun, waktu yang diperlukan untuk memusnahkan penyakit tersebut sangat lama yaitu lebih dari 200 tahun. Oleh karena itu, program vaksinasi yang dilakukan belum cukup efektif untuk mencegah penyebaran penyakit

Gambar tersebut juga menunjukkan bahwa untuk , semakin tinggi tingkat vaksinasi mengakibatkan titik tetap endemik akan semakin menurun. Dengan demikian, pada titik tetap endemik, semakin tinggi tingkat vaksinasi mengakibatkan proporsi individu infected akan semakin menurun.

Berdasarkan persamaan yang diperoleh, tingkat vaksinasi yang dilakukan harus cukup lebih besar dari tingkat vaksinasi minimum agar penyebaran penyakit dapat dicegah dengan sukses.

Selanjutnya, tingkat vaksinasi dilakukan pada tingkat . dan kemudian dinaikkan lagi untuk mengetahui pengaruh vaksinasi pada tingkat . maka proporsi individu infected disajikan pada Gambar 6.

Selanjutnya, jika setiap kelahiran memperoleh vaksin maka nilai . Jika

[image:31.612.336.502.482.665.2]

maka proporsi individu infected disajikan pula pada Gambar 6.

(32)

9

Sedangkan jika . penyakit akan menghilang dalam waktu kurang lebih 20 tahun. Dalam waktu kurang lebih 50 tahun, sistem akan setimbang saat:

, . ,

Titik tetap yang dimaksud adalah titik tetap bebas penyakit karena proporsi individu

infected bernilai nol. Besarnya bilangan

reproduksi vaksinasi adalah . . Titik tetap bebas penyakit tersebut bersifat stabil asimptotis karena .

Gambar tersebut juga menunjukkan bahwa penyakit akan menghilang dari populasi dalam waktu kurang lebih 18 tahun jika .

Titik tetap, bilangan reproduksi vaksinasi , dan kestabilan untuk , . ,

[image:32.612.335.505.157.290.2]

. , , . , . , dan disajikan pada Tabel 2.

Tabel 3. Titik tetap, bilangan reproduksi vaksinasi, dan kestabilan untuk , . ,

. , , . , . , dan

Titik Tetap Kestabilan 0 (0.5375,0.4302) 1.86 stabil

asimptotis (0.5375,0) 1 stabil 0.6 (0.4,0) 0.74 stabil

asimptotis 0.9 (0.1,0) 0.19 stabil

asimptotis

1 (0,0) 0 stabil

asimptotis

Tabel 3 menunjukkan bahwa semakin tinggi tingkat vaksinasi maka bilangan reproduksi vaksinasi akan semakin menurun. Penurunan tersebut menyebabkan proporsi individu infected pada titik tetap juga menurun. Tabel 3 juga menunjukkan bahwa untuk , kenaikan tingkat vaksinasi menyebabkan proporsi jumlah individu susceptible pada titik tetap akan menurun. Selanjutnya, untuk , pada titik tetap, proporsi individu susceptible bernilai nol. Hal ini menunjukkan bahwa semua individu telah kebal dari penyakit dan memasuki subpopulasi recovered. Titik tetap yang dicapai adalah titik tetap bebas penyakit karena nilai proporsi individu infected pada titik tersebut adalah nol.

Kriteria kestabilan di titik tetap dapat digambarkan dengan plot bidang fase

susceptible-infected. Sebagai contoh,

ditunjukkan kestabilan pada titik tetap untuk . . Titik tetap utuk . adalah titik tetap endemik:

. , .

Plot bidang fase untuk . disajikan pada Gambar 7.

Gambar 7. Plot bidang fase untuk .

Gambar 7 menunjukkan bahwa semua plot bidang fase menuju ke arah titik tetap endemik. Oleh karena itu, titik tetap endemik tersebut bersifat stabil asimptotis.

Selanjutnya, akan ditunjukkan kestabilan pada titik tetap untuk . Titik tetap untuk

adalah titik tetap bebas penyakit: ,

[image:32.612.127.318.292.487.2] [image:32.612.333.505.432.569.2]

Plot bidang fase untuk ditujukan pada Gambar 8.

Gambar 8. Plot bidang fase untuk

Gambar 8 menunjukkan bahwa semua plot bidang fase meuju ke arah titik tetap bebas penyakit. Oleh karena itu, titik tetap bebas penyakit bersifat stabil asimptotis.

Untuk mengamati pengaruh vaksinasi terhadap dinamika populasi individu rentan dan terinfeksi pada waktu tertentu maka diperlukan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi dengan variabel waktu. Hal ini membutuhkan

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.1 0.2 0.3 0.4 0.5 0.6 Susceptible In fe ct ed

(33)

10

nilai awal untuk semua parameter dan variabel.

Pada proses penggambarannya diambil nilai awal populasi individu yang rentan dan terinfeksi masing-masing adalah 80% dan 20%.

Pada bagian ini dianalisis dinamika populasi untuk dua kondisi yaitu perubahan parameter yang menunjukkan laju penularan penyakit dan perubahan parameter

yang menunjukkan laju kesembuhan dengan tingkat vaksinasi .

Proses penggambarannya dengan menggunakan Maple 13 yang dievaluasi ketika . , . , dan . dengan nilai awal . , . , dan

.

[image:33.612.332.504.79.283.2]

Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi di bawah ini,

Gambar 9. Dinamika populasi infected untuk . , . ,dan .

Gambar 9 menunjukkan hubungan populasi infected terhadap waktu t. Kurva di atas dibandingkan berdasarkan nilai yang berbeda yaitu . , . , dan . . Dari kurva di atas dapat dilihat bahwa individu rentan dan yang terinfeksi mengalami penurunan terus menuju nol yang artinya menuju kepunahan. Semakin besar nilai , pada awal kurva tersebut semakin ke atas, artinya laju penularan penyakit ketika . lebih besar dari laju penularan penyakit ketika

. dan laju penularan penyakit ketika . lebih besar dari laju penularan penyakit ketika . dan . . Ini berarti bahwa ketika laju penularan penyakit meningkat mengakibatkan banyaknya individu yang terinfeksi juga meningkat.

Gambar 10. Dinamika populasi infected untuk

. , . , dan

.

Gambar 10 menunjukkan hubungan populasi infected terhadap waktu t. Kurva di atas dibandingkan berdasarkan nilai yang berbeda yaitu . , . , dan . . Dari kurva di atas dapat dilihat bahwa individu rentan dan yang terinfeksi mengalami penurunan terus menuju nol yang artinya menuju kepunahan. Semakin besar nilai , pada awal kurva tersebut semakin ke bawah, artinya laju kesembuhan penyakit ketika

[image:33.612.138.305.309.499.2]

(34)

IV.

SIMPULAN

Dalam karya tulisi ini dianalisis pengaruh vaksinasi terhadap model epidemik SIR. Sebagai hasil analisis kesetimbangan model ini diperoleh dua titik tetap, yaitu titik tetap bebas penyakit dan titik tetap endemik. Analisis kestabilan titik tetap bebas penyakit dan titik tetap endemik masing-masing bersifat tidak stabil dan stabil asimptotis.

Pada penerapan kasus, model SIR tersebut dibedakan menjadi dua macam yaitu dengan dipengaruhi vaksinasi dan tanpa dipengaruhi vaksinasi. Pengaruh tingkat vaksinasi pada penyebaran penyakit untuk tingkat vaksinasi di bawah ambang vaksinasi, semakin besar tingkat vaksinasi akan menyebabkan proporsi individu infected pada titik tetap semakin

kecil. Untuk tingkat vaksinasi di atas ambang vaksinasi, semakin besar tingkat vaksinasi menyebabkan proporsi individu susceptible pada titik tetap semakin kecil dan penyakit akan menghilang dari populasi dalam waktu yang lebih cepat. Pengaruh vaksinasi terhadap dinamika individu rentan dan yang terinfeksi yaitu ketika laju penularan penyakit meningkat mengakibatkan banyaknya individu yang terinfeksi juga meningkat. Selanjutnya, ketika laju kesembuhan penyakit meningkat mengakibatkan banyaknya individu yang terinfeksi menurun.

DAFTAR PUSTAKA

Bellomo N. and Preziosi L. 1995. Mathematical Modeling. CRC Press, Florida.

Farlow SJ. 1994. An Introduction to Differential Equation and Their Application. Mc Graw-Hill, New York. Giesecke J. 1994. Modern Infectious Disease

Epidemiology. Oxford University Press, New York.

Hethcote HW. 2000. The Mathematics of Infectious Diseases. SIAM Review. no. 4. pp. 599-653.

Makinde OD. 2007. Adomian Decomposition Approach to a SIR Epidemic Model with Constant Vaccination Strategy. Comput. Appl. Math. 184. pp. 842-848.

Strogatz SH. 1994. Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. Addison-Wesley Publishing Company, Reading, Massachusete.

Tu PNV. 1994. Dynamical System, An Introduction with Application in Economics and Biology. Springer-Verlag. Heidelberg, Germany.

UNICEF. 2007. Polio: Stories from West

Java. http: // www.unicef.org

/indonesia/reallives_2956.html di akses pada tanggal 12 September 2010.

WHO. 2007. Measles. http: // www.who.int /mediacentre/factsheets/fs286/en/ di akses pada tanggal 12 September

(35)

(36)

13

Lampiran 1. Pencarian Titik Tetap Sistem Persamaan (3.8) Titik tetap diperoleh dengan menyederhanakan:

Sehingga:

Dari , diperoleh:

 Jika , maka