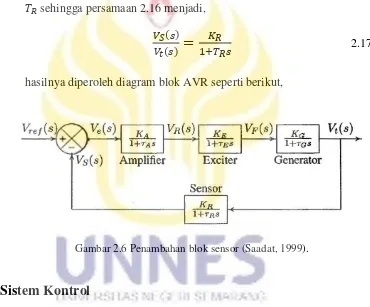
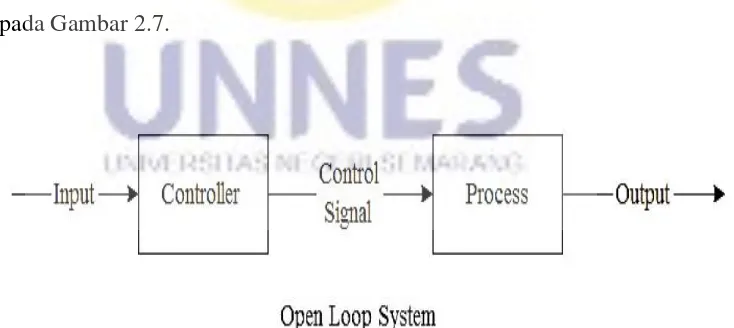
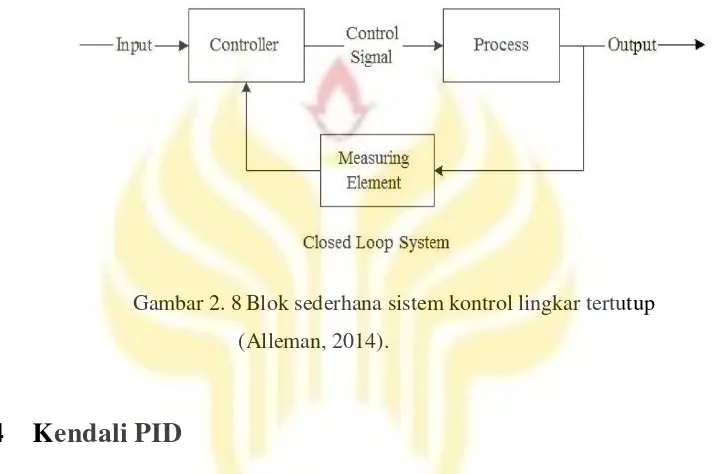
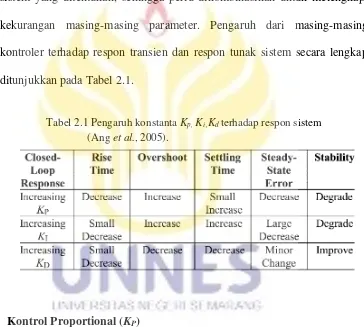
SIMULASI KENDALI PID DAN LOGIKA FUZZY PADA SISTEM EKSITASI AUTOMATIC VOLTAGE REGULATOR DENGAN SIMULINK MATLAB -
Teks penuh
Gambar
Dokumen terkait
Mengingat lokasi objek yang berada di kota Surabaya yang merupakan kota besar di Jawa Timur dan menjadi ibukota propinsi, serta menjadi pusat berbagai industri di Jawa timur,
Perbedaan karakter sikap dan perilaku dapat menyebabkan tidak sejalannya proses interaksi yang terjadi.Banyaknya perbedaan dalam suatu interaksi masyarakat bisa timbul
6 | P a g e dalam hubungan-hubungan sosial yang sama artinya dengan pengertian adaptasi (adaptation) yang dipergunakan oleh ahli-ahli biologi untuk menunjuk pada
Menunjukkan pada stakeholders manfaat suatu kebijakan: apabila tidak dilakukan evaluasi terhadap sebuah kebijakan, para stakeholders, terutama kelompok sasaran tidak
emang kenalnya dari tempat dugem sih, tapi kadang kita meskipun nggak lagi dugem masih tetep komunikasi kok, kadang juga nongkrong bareng trus lagi kalo lagi butuh
Para komunitas yang digandeng berhasil menyebarkan informasi kegiatan Strategic Communication Museum Kereta Api Ambarawa, melalui akun sosial media mereka Menulis
Algoritma Min-mAx merupakan algoritma yang digunakan untuk menemukan langkah terbaik dalam permainan catur, sedangkan Algoritma Alpha Beta Pruning adalah algoritma
Berdasarkan uji hipotesis yang telah dilakukan, dapat disimpulkan bahwapersepsi pelanggan terkait implementasi prinsip etika bisnis islam berpengaruh positif dan