Barisan sebagai Fungsi sumardyono marfuah
Teks penuh
Gambar
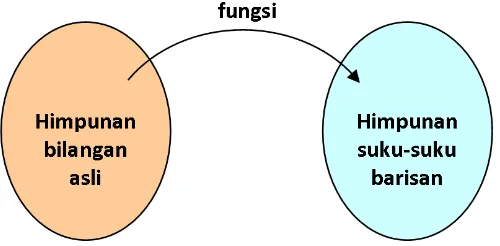
Dokumen terkait
Dengan membaca teks yang ada pada tayangan powerpoint, siswa dapat menunjukkan ungkapan atau kalimat saran, (sederhana) dengan percaya diri.. Dengan membaca teks yang ada pada
Kegiatan penelitian mini riset di SMA Unggul Negeri Subulussalam, penulis memberikan angket kepada beberapa dewan guru, hasil angket yang dijawab para dewan
Desa wisata adalah desa yang memiliki potensi keunikan dan daya tarik wisata yang khas, baik berupa karakter fisik lingkungan alam pedesaan maupun kehidupan sosial
Kemerdekaan dalam memilih jodoh telah ditegaskan dalam Islâm melalui pernyataan Rasûlullâh SAW ketika beliau didatangi oleh seorang gadis sambil mengadukan tentang
Untuk mengkaji perbedaan keterampilan generik siswa pada pembelajaran biologi materi keanekaragaman makhluk hidup antara pengunaan media p embelajaran Adobe Captivate
• Meneruskan lawatan ST.SOPHIA , TOPKAPI PALACE HIPPODROME, BLUE MOSQUE • Makan Tengahari Di Restoran Tempatan. • Solat Jamak & Qasar di masjid tempatan • Membeli belah
Tujuan dari diadakannya Pengabdian Kepada Masyarakat dengan judul “Pelatihan Penggunaan Model Pembelajaran Jurisprudensial Pada Guru Di KB TK Surya Marta
Dengan demikian, unsur dan suasana yang membawa kepada persaingan yang menindas adalah diharamkan oleh Islam seperti monopoli dalam kegiatan produksi dan