Cambridge Pre-U Mathematics (9794)
Teks penuh
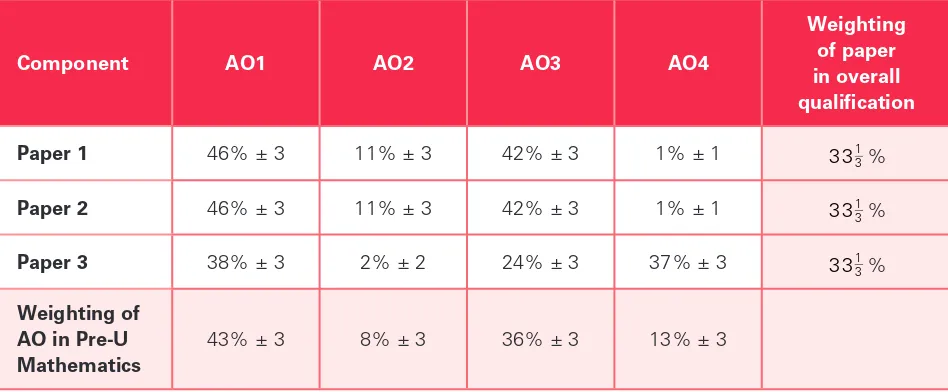
Gambar
Garis besar
Dokumen terkait
Candidates should be able to apply their knowledge of economic theory to explain potential conl icts between policy objectives, including the historical Phillips Curve
Candidates will demonstrate in-depth knowledge and critical understanding of relevant business theories and concepts and apply this knowledge to business problems and issues
Candidates will demonstrate in-depth knowledge and critical understanding of relevant business theories and concepts and apply this knowledge to business problems and issues
– demonstrate and communicate using some appropriate terminology a good level of knowledge and critical understanding of a range of psychological studies, theories, concepts,
These topic areas are intended to help candidates and not limit them, and where the subject matter is the personal choice of candidates, for example the Prepared Topic in the
• candidates show sound knowledge and understanding of linguistic structures and demonstrate accurate comprehension and interpretation of the prescribed Latin literature,
eschi’s Judit ull reference Capodimonte e e candidates or more eptember 20 administratio. de of the
> 93% 15 > 87% 14 • correct selection, recall and use of facts, rules, definitions and procedures; comprehension and clear communication of mathematical concepts and techniques;