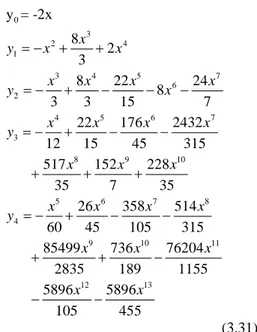METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERSAMAAN DIFERENSIAL ABELIAN HAPSARI SYAMSIDAR YUSANTO

(1)

METODE DEKOMPOSISI ADOMIAN

UNTUK MENYELESAIKAN

PERSAMAAN DIFERENSIAL ABELIAN

HAPSARI SYAMSIDAR YUSANTO

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2009

(2)

ABSTRACT

HAPSARI SYAMSIDAR YUSANTO. Adomian Decomposition Method for Solving Abelian Differential Equation. Supervised by JAHARUDDIN and ALI KUSNANTO.

In this writing, Adomian Decomposition Method is used for solving Abelian Differential Equation. Abelian Differential Equation is a nonlinear differential equation which is hard to solve analytically. A special case of Abelian Differential Equation is oftenly used to model the population growth of deer in a certain place.

In this research, a numerical equation to solve Abelian Differential Equation is constructed using Adomian Decomposition Method. Furthermore, the validity of the results will be compared with the exact solution and numerical using fourth order Runge-Kutta method. The numerical results show that Adomian Decomposition Method is suitable for solving Abelian Differential Equation. Beside that, the procedure of Adomian Decomposition Method is used to solve the population growth of deer in a certain place.

(3)

ABSTRAK

HAPSARI SYAMSIDAR YUSANTO. Metode Dekomposisi Adomian untuk Menyelesaikan Persamaan Diferensial Abelian. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO

Dalam tulisan ini digunakan Metode Dekomposisi Adomian untuk menyelesaikan Persamaan Diferensial Abelian. Persamaan Diferensial Abelian merupakan suatu persamaan diferensial taklinear yang secara analitik sulit ditentukan solusinya. Salah satu model dalam bentuk Persamaan Diferensial Abelian muncul pada masalah pertumbuhan populasi rusa pada suatu wilayah.

Dalam tulisan ini dikonstruksi suatu persamaan numerik untuk menyelesaikan Persamaan Diferensial Abelian dengan menggunakan Metode Dekomposisi Adomian. Selanjutnya, dikaji validitas Metode Dekomposisi Adomian dengan cara membandingkan solusi Metode Dekomposisi Adomian dengan solusi eksak dan solusi numerik menggunakan metode Runge-Kutta orde empat untuk beberapa contoh kasus. Hasil numerik yang diperoleh menunjukkan bahwa Metode Dekomposisi Adomian cocok digunakan untuk menyelesaikan Persamaan Diferensial Abelian. Selain itu, prosedur dari Metode Dekomposisi Adomian digunakan untuk menyelesaikan masalah pertumbuhan populasi rusa pada suatu wilayah.

(4)

METODE DEKOMPOSISI ADOMIAN

UNTUK MENYELESAIKAN

PERSAMAAN DIFERENSIAL ABELIAN

HAPSARI SYAMSIDAR YUSANTO

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(5)

PRAKATA

ALHAMDULILLAH, segala puji dan syukur penulis ucapkan kepada Allah SWT yang telah memberikan limpahan rahmat dan hidayah-Nya sehingga dapat terselesaikannya karya ilmiah ini. Shalawat serta salam senantiasa selalu tercurahkan untuk Nabi Muhammad SAW yang telah mengantarkan kita semua umatnya sehingga dapat memperoleh petunjuk jalan yang benar, beserta keluarganya, para sahabat, dan semoga tercurahkan juga untuk kita semua sebagai umatnya hingga akhir zaman. Penulis menyampaikan terima kasih yang sebesar-besarnya kepada:

1. Mama, Bapak, mas Topan, Lella, Shandy, dan adik kembar Ghany-Zaky, atas doa, semangat, motivasi, dan perhatiannya hingga penulis dapat menyelesaikan karya ilmiah ini. Juga kepada keluarga besar, mbah kakung, om-tante dari keluarga mama dan bapak.

2. Bapak Dr. Jaharuddin, MS dan Bapak Drs. Ali Kusnanto, M.Si masing-masing selaku Pembimbing I dan Pembimbing II, atas kesabaran dan kemurahan hatinya dalam membimbing penulis hingga karya ilmiah ini dapat diselesaikan. Terima kasih juga diberikan untuk semua ilmu, saran, motivasi, serta waktu yang diluangkan untuk memberikan bimbingan kepada penulis.

3. Bapak Drs. Siswandi, M.Si selaku dosen penguji.

4. Dosen-dosen Departemen Matematika yang telah memberikan dan menyampaikan ilmunya yang bermanfaat kepada penulis, khususnya kepada Bu Ida, Bu Endar, Bu Ati, Bu Anggi, Pak Budi, Pak Wayan, Pak Effendi, Pak Siswadi.

5. Staf Departemen Matematika yang telah memberikan bantuan dan semangatnya, khususnya kepada Pak Yono, Mas Bono, Bu Ade, Mas Deni, Mas Heri, Bu Susi. 6. Keluarga besar Cirebon, atas doa dan dukungannya, khususnya mas Nunung

yang selalu memberikan doa, saran, semangat yang tiada hentinya kepada penulis.

7. Achy dan Oby, sebagai dua “Angel” penulis.

8. Sahabat Math’42: Idun, Lisda, Yusep, Iput, Vita, Jane, Hikmeh, Titi, Vera, Ily, mb Vin, Didi, Okta, Ryu, Luri, Siti, Rima, Mira, Acuy, Eko, Danu, Ocoy, Nyomi, Keni, Agnes, Hesti, Nola, Tia, Lela, Pipit, Dendy, Yudi, Boy, Sapto, Septian, ms War, Ridwan, Kinun, Awi, Djawa, Ardy pake Y, Moko, Eyi, Erlyn, Agem, Ety, Lina, Rita, Gita, Kinun, Bayu, Fachry, ms Ayip, Heri. Terima kasih atas kebersamaan dan kenangan-kenangan manis yang telah dilalui bersama dalam satu wadah mate 42.

9. Anak-anak kosan Ixora: K’icut, K’winni, K’eki, K’rohmah, K’vera, Evi, Dc, Erni, atas doa dan dukungannya.

10. Seluruh civitas matematika, GUMATIKA, semoga selalu kompak dalam membawa nama harum Matematika.

Dengan tidak mengurangi rasa hormat, penulis juga menyampaikan terima kasih kepada pihak-pihak yang belum disebutkan satu per satu.

Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan, khususnya Matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, Oktober 2009 Hapsari Syamsidar Yusanto

(6)

Judul Skripsi : Metode Dekomposisi Adomian untuk Menyelesaikan Persamaan

Diferensial Abelian

Nama

: Hapsari Syamsidar Yusanto

NIM

:

G54052393

Menyetujui

Pembimbing I

Dr. Jaharuddin, MS.

NIP. 19651102 199302 1 001

Pembimbing II

Drs. Ali Kusnanto, M.Si.

NIP. 19650820 199003 1 001

Mengetahui

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA.

NIP. 19610328 198601 1 002

(7)

RIWAYAT HIDUP

Penulis dilahirkan di Semarang pada tanggal 1 Agustus 1987 sebagai anak kedua dari enam bersaudara. Penulis merupakan anak dari pasangan Gunawan Susanto dan Sri Juniti.

Penulis lulus dari SDN 06 Ngaliyan Kampus tahun 1999, lulus dari SLTPN 01 Semarang pada tahun 2003, tahun 2005 penulis menjadi alumni dari SMAN 05 Semarang. Terdaftar sebagai mahasiswa IPB pada tahun 2005 melalui jalur Undangan Seleksi Masuk IPB (USMI) Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama mengikuti perkuliahan, penulis pernah menjadi Asisten Dosen Mata Kuliah Kalkulus II dan III (2007-2008), menjadi staf pengajar di salah satu bimbingan belajar mahasiswa MSC. Dalam berorganisasi, penulis pernah menjadi koordinator acara TRY OUT SPMB se-Bogor (Maret 2007), kepala departemen Sosinkom GUMATIKA (2006-2007), koordinator PAK pada Welcome Ceremony Mathematics (WCM) angkatan 43, anggota sie Acara pada WCM 44.

(8)

viii

DAFTAR ISI

Halaman Daftar Gambar ... ix Daftar Tabel ... ix Daftar Lampiran ... ix I PENDAHULUAN ... 1 1.1 Latar Belakang ... 1 1.2 Tujuan Penulisan ... 1 1.3 Sistematika Penulisan ... 1 II LANDASAN TEORI ... 2

2.1 Metode Pemisahan Variabel ... 2

2.2 Metode Runge-Kutta Orde Empat ... 2

2.3 Metode Iterasi Picard ... 3

2.4 Deret Maclaurin ... 4

III PEMBAHASAN ... 5

3.1 Formulasi masalah ... 5

3.2 Metode Dekomposisi Adomian ... 5

3.3 Aplikasi pada Persamaan Diferensial Abelian ... 6

3.4 Aplikasi pada Model Pertumbuhan Populasi Rusa ... 10

IV KESIMPULAN ... 12

DAFTAR PUSTAKA ... 12

LAMPIRAN ... 13

(9)

DAFTAR GAMBAR

Halaman

1 Perbandingan Solusi Eksak dan Solusi Hampiran Masalah Nilai Awal (2.9) ... 3

2 Perbandingan Solusi Eksak dan Solusi Hampiran Masalah Nilai Awal (2.14) ... 4

3 Perbandingan Grafik Solusi Masalah Nilai Awal (3.26) dengan Metode Dekomposisi Adomian untuk n = 5 dan Metode Runge-Kutta Orde Empat ... 8

6 Perbandingan Grafik Solusi Masalah Nilai Awal (3.29) dengan Metode Dekomposisi Adomian untuk n = 5 dan Solusi Eksak ... 9

9 Perbandingan Grafik Solusi Masalah Nilai Awal (3.33) Metode Dekomposisi Adomian dan Solusi Numerik ... 11

10 Bidang Fase Pertumbuhan Populasi Rusa dengan M = 100 dan m = 7 ... 11

DAFTAR TABEL

Halaman 1 Galat Hampiran Solusi Masalah Nilai Awal (2.9) ... 3

2 Galat Hampiran Solusi Masalah Nilai Awal (2.14) ... 4

3 Galat Hampiran Solusi Masalah Nilai Awal (3.26) untuk Orde yang Berbeda ... 9

4 Galat Hampiran Solusi Masalah Nilai Awal (3.29) untuk Orde yang Berbeda ... 10

DAFTAR LAMPIRAN

Halaman 1 Penurunan Persamaan (2.10) ... 14 2 Penurunan Persamaan (3.8) ... 15 3 Penurunan Persamaan (3.11) ... 15 4 Penurunan Persamaan (3.22) ... 16 5 Penurunan Persamaan (3.24) ... 16 6 Penurunan Persamaan (3.27) ... 17 7 Penurunan Persamaan (3.28) ... 17

8 Syntax MATLAB 7.0.1 untuk Menyelesaikan Contoh 1 ... 18

9 Penurunan Persamaan (3.30) ... 19

11 Syntax MATLAB 7.0.1 untuk Menyelesaikan Contoh 2 ... 20

14 Syntax Mathematica 6 untuk Menyelesaikan Model Pertumbuhan Populasi Rusa ... 22

(10)

I PENDAHULUAN

1.1 Latar Belakang

Dalam berbagai cabang ilmu pengetahuan seperti sosial, fisika, biologi, dan kimia bahkan dalam kehidupan sehari-hari seringkali muncul suatu permasalahan yang dapat dimodelkan ke dalam suatu model matematika. Salah satu model matematika yang banyak digunakan adalah persamaan diferensial. Model dalam bentuk persamaan diferensial sering muncul pada berbagai masalah, seperti masalah pendeteksian suatu karya seni, persentase peningkatan kelompok ikan hiu yang hidup di laut mediterania, mendiagnosis diabetes, dan penyebaran

gonorrhea (Braun 1993).

Beberapa model dalam bentuk persamaan diferensial berupa persamaan diferensial biasa dan persamaan diferensial parsial. Persamaan diferensial biasa adalah persamaan diferensial yang memuat satu variabel bebas, sedangkan persamaan diferensial parsial adalah persamaan diferensial yang memuat lebih dari satu variabel bebas. Beberapa contoh model dari persamaan diferensial biasa ditemukan dalam dinamika populasi penduduk, penyerapan zat-zat yang bersifat radiasi, peluruhan suatu zat yang bersifat radioaktif, pengukuran suhu, reaksi-reaksi kimia, dan hal-hal yang berhubungan dengan ekonomi. Beberapa contoh model dari persamaan diferensial parsial, di antaranya digunakan untuk model arus lalu lintas di jalan yang ramai, aliran darah melalui tabung elastis tembok, dan gelombang kejut sebagai kasus khusus dari teori umum gas dinamika hidrolik (Wazwaz 2002).

Beberapa penelitian telah dilakukan untuk memperoleh solusi dari masalah yang dimodelkan dalam bentuk persamaan diferensial. Salah satu metode untuk memperoleh solusi dari model matematika tersebut adalah Metode Dekomposisi Adomian. Metode Dekomposisi Adomian merupakan salah satu metode yang akan dibahas dalam tulisan ini. Metode ini telah digunakan untuk memperoleh solusi dari sistem persamaan diferensial linear maupun taklinear dengan orde yang besar (Adomian 1994). Dalam metode ini, solusi persamaan diferensial dimisalkan dalam bentuk deret. Kekonvergenan deret dalam metode ini telah dikaji oleh beberapa peneliti, di antaranya Abbaoui dan Cherruault (1996), Seng et al

(1996), Cherruault (1989), serta Cherruault dan Adomian (1993). Mereka mengkaji kriteria agar kekonvergenan deret dapat cepat tercapai. Abbaoui dan Cherruault telah mengusulkan suatu bukti mengenai kekonvergenan deret pada dekomposisi Adomian (Adomian 1988).

Berdasarkan hal tersebut di atas, maka dalam tulisan ini akan dibahas penggunaan Metode Dekomposisi Adomian pada model persamaan berupa Persamaan Diferensial Abelian. Salah satu kasus khusus dari Persamaan Diferensial Abelian adalah Persamaan Diferensial Riccati. Persamaan Diferensial Riccati banyak muncul pada masalah kontrol optimum, dimana solusi Persamaan Diferensial Riccati digunakan sebagai fungsi transfer pada masalah kontrol optimum (Jaradat 2008). Selain itu, model dalam bentuk Persamaan Diferensial Abelian juga muncul pada masalah pertumbuhan populasi rusa pada suatu wilayah (Giordano dan Weir 1991).

1.2 Tujuan Penulisan

Berdasarkan uraian dalam latar belakang, tujuan dari penulisan ini adalah

a. Mengkonstruksi suatu persamaan numerik untuk menyelesaikan Persamaan Diferensial Abelian dengan menggunakan Metode Dekomposisi Adomian.

b. Mengkaji validitas Metode Dekomposisi Adomian dengan cara membandingkan dengan solusi eksak atau solusi dengan metode Runge-Kutta orde empat untuk beberapa contoh kasus.

1.3 Sistematika Penulisan

Tulisan ini terdiri dari empat bab. Bab pertama merupakan pendahuluan yang berisi tentang latar belakang dan tujuan penulisan. Bab kedua adalah landasan teori yang berisi tentang metode analitik dan numerik untuk menyelesaikan suatu masalah nilai awal atau masalah nilai batas. Bab ketiga merupakan pembahasan yang berisi tentang analisis metode yang digunakan dalam tulisan ini serta aplikasi dan hasil numerik yang didalamnya membahas tentang Metode Dekomposisi Adomian. Validitas dari metode ini juga dibahas dalam bab ini. Bab terakhir berupa kesimpulan dari keseluruhan tulisan ini.

(11)

II LANDASAN TEORI

Persamaan diferensial merupakan

persamaan yang memuat turunan dari suatu fungsi. Bila fungsi tersebut tergantung pada satu variabel bebas, maka disebut Persamaan Diferensial Biasa (PDB), sedangkan bila fungsi tersebut memuat lebih dari satu variabel bebas, maka disebut Persamaan Diferensial Parsial (PDP).

Bentuk umum PDB linear orde ke-n adalah ( ) 1 0 ( ) n ( ) ' ( ) ( ) n a x y + +… a x y+a x y= f x dengan a_n≠0, a xn( ),....,a x0( ) disebut

koefisien persamaan diferensial, sedangkan bila tidak dapat dinyatakan seperti bentuk di atas disebut persamaan diferensial taklinear.

Seringkali persamaan diferensial dilengkapi nilai awal atau nilai batas. Masalah persamaan diferensial yang dilengkapi dengan suatu nilai awal disebut masalah nilai awal. Sedangkan masalah persamaan diferensial yang dilengkapi dengan suatu nilai batas disebut masalah nilai batas.

Terdapat beberapa metode untuk menyelesaikan suatu masalah nilai awal atau masalah nilai batas. Secara analitik dapat digunakan metode pemisahan variabel, tetapi hanya untuk persamaan diferensial yang dapat dipisah. Secara numerik dapat digunakan metode Runge-Kutta orde empat dan metode iterasi Picard. Konsep dasar metode-metode tersebut akan disarikan dari pustaka (Sahid 2005) dan (Zwillinger 1992).

2.1 Metode Pemisahan Variabel

Metode pemisahan variabel digunakan dalam tulisan ini untuk memperoleh solusi dari masing-masing masalah nilai awal. Berikut ini merupakan konsep dasar dari metode pemisahan variabel. Misalkan diberikan persamaan diferensial biasa orde satu sebagai berikut

( ) ' ( ) f x y g y = , (2.1)

dengan nilai awal yang diberikan

0 0

( )

y x = y .

Dalam metode pemisahan variabel, persamaan (2.1) dinyatakan dalam persamaan berikut

( ) ( ) g y dy= f x dx.

(2.2) Selanjutnya, akan diperoleh solusi dari masalah nilai awal (2.1) dengan

mengintegralkan kedua ruas pada persamaan (2.2), sehingga diperoleh persamaan berikut

0

( ) ( ) g y dy= f x dx+y

∫

. (2.3)

Untuk memahami metode pemisahan variabel, tinjau contoh berikut. Misalkan diberikan persamaan diferensial orde satu berikut

' x

y y

= (2.4)

dengan nilai awal

(0) 1

y = .

Solusi dari masalah nilai awal (2.4) dapat dicari dengan menggunakan metode pemisahan variabel yang dinyatakan dalam persamaan berikut

y dy=x dx (2.5) dengan solusi berbentuk

2 2 1

y =x + (2.6) atau secara eksplisit dapat juga dinyatakan dalam persamaan berikut

2

( ) 1

y x = ± +x .

2.2 Metode Runge-Kutta Orde Empat

Salah satu metode numerik yang digunakan pada tulisan ini adalah metode Runge-Kutta orde empat. Metode ini digunakan sebagai pembanding dari metode yang akan dikaji khususnya pada masalah nilai awal atau masalah nilai batas yang sulit diselesaikan secara analitik. Tinjau masalah nilai awal berikut

' ( , )

y = f x y , (2.7)

dengan nilai awal

0 0

( )

y x =y .

Solusi masalah nilai awal (2.7) dapat dilakukan dengan metode Runge-Kutta orde empat yang dirumuskan sebagai berikut

[

]

1 1 2 3 4 ( ) ( ) 2( ) 6 k k h y x₊ = y x + S + S +S +S (2.8) dengan 1 2 1 3 2 4 3 ( , ) ( / 2, / 2), ( / 2, / 2), ( , ) k k k k k k k k S f x y S f x h y hS S f x h y hS S f x h y hS = = + + = + + = + + 1 k k h=x −x₋ .

(12)

3

Untuk memahami metode Runge-Kutta orde empat, tinjau contoh berikut.

Misalkan diberikan persamaan diferensial biasa orde satu berikut

2 ' 2

y = xy+xy pada [0,1] , (2.9) dengan nilai awal

(0) 1

y = .

Lebar langkah yang digunakan dalam metode ini dimisalkan h = 0.05. Rumus-rumus Si pada metode Runge-Kutta orde

empat adalah

(

)(

) (

)(

)

2 1 0 0 0 0 2 1 1 2 0 0 0 0 2 2 2 3 0 0 0 0 2 4 0 0 3 0 0 3 2 , 2 , 2 2 2 2 2 , 2 2 2 2 2 . S x y x y h S h S S x y h x y h h S h S S x y h x y h S x h y hS x h y hS = + ⎛ ⎞⎛ ⎞ ⎛ ⎞⎛ ⎞ = _⎜ + _⎟⎜ + _{⎟ ⎜}+ + _⎟⎜ + _⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎛ ⎞⎛ ⎞ ⎛ ⎞⎛ ⎞ = _⎜ + _⎟⎜ + _{⎟ ⎜}+ + _⎟⎜ + _⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠⎝ ⎠ = + + + + +

Jadi rumus rekursif suku-suku yn berdasarkan

persamaan (2.8) adalah

(

)

1 1 2 3 4 ( ) ( ) 2 6 k k h y x+ =y x + ⎡⎣S + S +S +S ⎤⎦.

Solusi eksak masalah nilai awal (2.9) adalah 2 2 2 ( ) 3 x x e y x e = − . (2.10) Penurunan persamaan (2.10) dapat dilihat pada Lampiran 1.

Gambar 1 berikut ini merupakan grafik dari solusi eksak dan solusi hampiran dari masalah nilai awal (2.9) dengan menggunakan metode Runge-Kutta orde empat.

Gambar 1 Perbandingan solusi eksak dan solusi hampiran masalah nilai awal (2.9).

Berdasarkan Gambar 1 disimpulkan bahwa metode Runge-Kutta orde empat cocok digunakan untuk menyelesaikan suatu

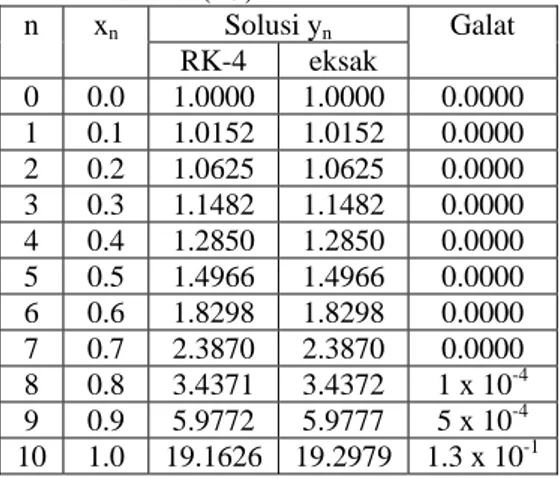
masalah nilai awal atau masalah nilai batas dengan ketelitian yang tinggi. Ketelitian metode ini pada masalah nilai awal (2.9) diberikan pada Tabel 1.

Tabel 1 Galat hampiran solusi masalah nilai awal (2.9) n xn Solusi yn Galat RK-4 eksak 0 0.0 1.0000 1.0000 0.0000 1 0.1 1.0152 1.0152 0.0000 2 0.2 1.0625 1.0625 0.0000 3 0.3 1.1482 1.1482 0.0000 4 0.4 1.2850 1.2850 0.0000 5 0.5 1.4966 1.4966 0.0000 6 0.6 1.8298 1.8298 0.0000 7 0.7 2.3870 2.3870 0.0000 8 0.8 3.4371 3.4372 1 x 10-4 9 0.9 5.9772 5.9777 5 x 10-4 10 1.0 19.1626 19.2979 1.3 x 10-1 2.3 Metode Iterasi Picard

Metode iterasi Picard merupakan metode yang menghasilkan suatu solusi secara numerik pada suatu masalah nilai awal. Misalkan diberikan persamaan diferensial biasa orde satu sebagai berikut

' ( , )

y = f x y , (2.11)

dengan nilai awal

0 0

( )

y x =y .

Persamaan diferensial (2.11) dapat juga dinyatakan dalam bentuk persamaan integral berikut 0 0 ( ) ( , ( )) x x y x =y +

∫

f z y z dz. (2.12)

Solusi persamaan integral (2.12) dapat diperoleh dengan menggunakan metode iterasi Picard. Misalkan diberikan hampiran awal

0( ) 0

y x =y yang akan digunakan untuk mendekati hampiran suku berikutnya. Dengan mensubstitusi y x₀( ) ke dalam ruas kanan persamaan (2.12) diperoleh 0 1( ) 0 ( , 0( )) x x y x =y +

∫

f z y z dz.

Selanjutnya, y x₁( ) digunakan sebagai hampiran awal untuk memperolehy x2( ), dan seterusnya. Solusi hampiran y x₁( ) yang diperoleh merupakan solusi hampiran yang lebih baik dari hampiran sebelumnya yaitu

0( )

y x . Secara umum, diperoleh hampiran ke-(n+1) dari hampiran ke-n dengan mengikuti aturan rekursif berikut

0 1( ) 0 ( , ( )) , 0 x n n x y+ x = y +

∫

f z y z dz n≥ . 0 0.2 0.4 0.6 0.8 1 1.2 1.4 0 2 4 6 8 10 12 14 16 18 20 metode Runge-Kutta solusi eksak

(13)

(2.13) Dengan demikian diperoleh barisan hampiran solusi y x y x y x0( ), 1( ), 2( ),…. Barisan ini akan konvergen ke suatu fungsi yang menunjukkan solusi dari masalah nilai awal.

Untuk memahami metode iterasi Picard, tinjau contoh berikut.

Misalkan diberikan persamaan diferensial biasa orde satu berikut

'

y =xy, (2.14) dengan nilai awal

(0) 1

y = .

Solusi dari masalah nilai awal (2.14) dapat dicari dengan menggunakan metode iterasi Picard yang didasarkan pada persamaan (2.13) yaitu

(

)

1 0 0 ( ) x n n y₊ = y +

∫

xy z dz. (2.15) Dengan menggunakan aturan rekursif pada persamaan (2.15) diperoleh 0 2 1 2 4 2 4 6 2 4 6 8 4 2 4 6 8 1 3 0 2 5 1 1 2 1 2 8 1 2 8 48 1 2 8 48 384 1 2 8 48 384 3840 . y x y x x x x x x x x x y x x x x y y x y = = + + + + + + = + + + + = + + + + + = =

Solusi eksak masalah nilai awal (2.14) yaitu 2 2 ( ) x y x =e .

Gambar 2 berikut ini merupakan grafik dari solusi eksak dan solusi hampiran dari masalah nilai awal (2.14) dengan menggunakan metode iterasi Picard.

Gambar 2 Perbandingan solusi eksak dan solusi hampiran masalah nilai awal (2.14).

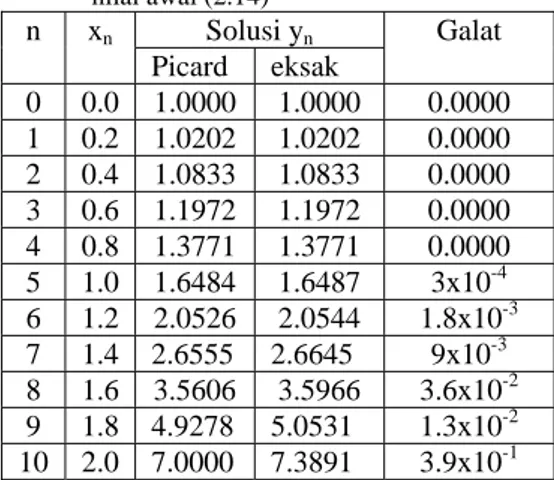
Berdasarkan Gambar 2 disimpulkan bahwa metode iterasi Picard cocok digunakan untuk menyelesaikan suatu masalah nilai awal atau masalah nilai batas dengan ketelitian yang tinggi. Ketelitian metode ini pada masalah nilai awal (2.14) diberikan pada Tabel 2.

Tabel 2 Galat hampiran solusi masalah nilai awal (2.14) n xn Solusi yn Galat Picard eksak 0 0.0 1.0000 1.0000 0.0000 1 0.2 1.0202 1.0202 0.0000 2 0.4 1.0833 1.0833 0.0000 3 0.6 1.1972 1.1972 0.0000 4 0.8 1.3771 1.3771 0.0000 5 1.0 1.6484 1.6487 3x10-4 6 1.2 2.0526 2.0544 1.8x10-3 7 1.4 2.6555 2.6645 9x10-3 8 1.6 3.5606 3.5966 3.6x10-2 9 1.8 4.9278 5.0531 1.3x10-2 10 2.0 7.0000 7.3891 3.9x10-1

Penggunaan metode Runge-Kutta orde empat lebih efisien dibandingkan dengan metode iterasi Picard. Dalam metode iterasi Picard dibutuhkan orde yang tinggi untuk menghampiri solusi eksak dengan ketelitian yang tinggi. Hal ini tidak diperlukan pada metode Runge-Kutta orde empat.

2.4 Deret Maclaurin

Pada tulisan ini, deret Maclaurin digunakan untuk memperoleh polinomial Adomian dari Metode Dekomposisi Adomian. Deret Maclaurin dapat diperoleh dari deret Taylor. Uraian deret Taylor dari suatu fungsi

( )

f x di sekitar x=a dinyatakan sebagai berikut 2 ( ) 3 '( ) ''( ) ( ) ( ) ( - ) ( - ) 1! 2! '''( ) ( ) ( - ) ... ( - ) . 3! ! n n f a f a f x f a x a x a f a f a x a x a n = + + + + +

Jika a=0, maka diperoleh deret Maclaurin berikut 2 3 ( ) '(0) ''(0) '''(0) ( ) (0) 1! 2! 3! (0) ... . ! n n f f f f x f x x x f x n = + + + + + 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 1 2 3 4 5 6 7 8

metode iterasi Picard solusi eksak

(14)

III PEMBAHASAN

Pada bagian ini akan diformulasikan

masalah yang akan dibahas. Solusi masalah akan diselesaikan dengan Metode Dekomposisi Adomian. Selanjutnya, metode ini akan digunakan untuk menyelesaikan model yang dinyatakan dalam bentuk Persamaan Diferensial Abelian. Agar validitas metode ini terjamin, maka pada bagian ini akan dikaji beberapa contoh kasus. Metode Dekomposisi Adomian yang diterapkan dalam tulisan ini mengikuti pustaka ( Adomian 1991).

3.1Formulasi Masalah

Untuk mengkaji lebih lanjut Metode Dekomposisi Adomian, maka tinjau terlebih dahulu persamaan diferensial taklinear berikut

[ ( )] ( )

F y x =G x ,

(3.1) dengan F menyatakan operator turunan yang

bentuknya taklinear dan G merupakan fungsi yang diketahui, sedangkan y menyatakan fungsi yang akan ditentukan.

Misalkan bagian linear dari F dipisah menjadi dua bagian yaitu L dan R, dengan L

suatu operator yang mempunyai invers dan R

operator linear lainnya. Bagian taklinear dari

F, dimisalkan N. Jadi, persamaan diferensial (3.1) dapat ditulis menjadi

(L+ +R N y) =G (3.2) atau dapat juga ditulis menjadi

Ly= −G Ry−Ny. (3.3) Selanjutnya, dipilih operator turunan L

yang memuat turunan dengan orde tertinggi dan mempunyai invers, sedangkan R operator turunan linear lainnya yang mempunyai orde lebih kecil dari L.

Metode Dekomposisi Adomian dikonstruksi berdasarkan eksistensi dari invers

L yaitu L-1 (sebagai contoh, jika L d dx = , maka 1 0 ( ) ( ) x

L− ⋅ = ⋅

∫

ds). Jika kedua ruas pada persamaan (3.3) dikenakan operator L-1 dari kiri, maka diperoleh solusi takhomogen dari persamaan (3.3) berbentuk

1 1 1

y=L G− −L Ry− −L Ny− . Misalkan fungsi ( )h x merupakan solusi homogen dari persamaan (3.3) atau persamaan

0

Ly= , maka solusi umum dari persamaan diferensial (3.3) adalah

1 1 1

y= +h L G− −L Ry− −L Ny− . (3.4) Dengan demikian solusi persamaan diferensial yang diberikan pada persamaan (3.4) bergantung pada bentuk taklinearL Ny−1 . Karena adanya bentuk taklinear tersebut, maka persamaan diferensial (3.1) sulit diselesaikan secara analitik. Berdasarkan hal tersebut, maka disarankan menggunakan metode yang disebut Metode Dekomposisi Adomian, dengan bentuk taklinear Ny akan didekomposisi dengan cara yang diuraikan pada bagian selanjutnya.

3.2 Metode Dekomposisi Adomian

Pada metode ini, solusi persamaan diferensial (3.4) dimisalkan dalam bentuk uraian deret berikut

2 0 1 2 0 n n n y y λy λ y λ y ∞ = = + + + =

∑

, (3.5) dengan λ suatu parameter, sedangkan

0, 1, 2,..., n

y y y y fungsi yang akan ditentukan.

Jika operator taklinear N dikenakan pada y, maka diperoleh

2

0 1 2

( )

Ny=N y +λy +λ y + . (3.6) Dengan menggunakan uraian deret Maclaurin pada fungsi Ny dalam persamaan (3.6) terhadap λ diperoleh 2 0 1 2 0 n n n Ny A λA λ A λ A ∞ = = + + + =

∑

, (3.7) dengan 0 0 1 0 0 1 ! n n n A Ny d A Ny d d A Ny n d λ λ λ λ λ = = = = = = . Selanjutnya, misalkan Ny= f y( ), sehingga fungsi f merupakan fungsi polinomial yang diberikan oleh persamaan (3.7) dan f juga merupakan fungsi analitik. Fungsi polinomial ini disebut polinomial Adomian. Dengan demikian bentuk

(15)

, 0,1, 2,

i

A i= … pada persamaan (3.7) dapat dinyatakan sebagai berikut

0 0 1 1 0 2 1 2 2 0 0 3 1 3 3 0 1 2 0 0 ( ) '( ) '( ) ''( ) 2 '( ) ''( ) '''( ) 3! A f y A y f y y A y f y f y y A y f y y y f y f y = = = + = + + (3.8) Penurunan persamaan (3.8) dapat dilihat pada Lampiran 2.

Selanjutnya, misalkan 1

L Ry− dan 1

L Ny−

berorde λ, maka persamaan (3.4) dapat ditulis

1 1 1

y= +h L G− −λL Ry− −λL Ny− .

(3.9) Jika y pada persamaan (3.5) dan Ny pada persamaan (3.7) disubstitusikan ke dalam persamaan (3.9), maka diperoleh

0 1 2 1 1 0 1 2 2 2 1 2 0 1 2 ( ) y y y y A A y y h L G L R L A λ λ λ λ λ λ λ λ − − − ⎛ ⎛ + ⎞⎞ + + + ⎜_⎜ ⎜_⎜₊ ₊ ⎟_⎟⎟_⎟ ⎝ ⎠ ⎝ ⎠ − + + + = + − (3.10) Jika koefisien dari perpangkatan λ_dari persamaan (3.10) disamakan pada kedua ruas, maka koefisien dari 0 2

, , ,...

λ λ λ masing-masing memberikan persamaan berikut

1 0 1 1 1 0 0 1 1 2 1 1 ( ) ( ) ( ) ( ) y h L G y L Ry L A y L Ry L A − − − − − = + = − − = − − (3.11) Secara umum bentuk y n adalah

1 1

-1 -1

( ) ( ), 1

n n n

y = −L− Ry −L− A n≥ .

Penurunan persamaan (3.11) dapat dilihat pada Lampiran 3.

Selanjutnya, berikut ini akan ditunjukkan bahwa 0 1 2 0 n n y y y y y ∞ = = + + + =

∑

(3.12) merupakan solusi dari persamaan diferensial (3.1) atau persamaan diferensial (3.2).

Jika y pada persamaan (3.12) disubstitusikan ke dalam ruas kiri persamaan (3.1), maka diperoleh ruas kiri persamaan (3.1) berikut

[

]

[

]

0 1 0 1 2 2 0 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) R y R y L y L y L y R y N y N y N y + + ⎡ ⎤ + + + _{+ ⎢} _⎥ + ⎣ ⎦ + + + + (3.13) Berdasarkan persamaan (3.11), diperoleh

(

)

1 0 1 0 1 2 1 0 1 1 1 1 0 0 1 1 ( ) ( ) ( ) = ( ) L Ry L y L y L y L h L G L L A L Ry L L A L h G Ry A Ry A − − − − − ⎛− −⎞ + + + = + + ⎜_⎜ ⎟_⎟+ − ⎝ ⎠ ⎛− −⎞ + ⎜ ⎟ ⎜ ₋ ⎟ ⎝ ⎠ + − − − − − (3.14) Selain itu, dari persamaan (3.6) dan (3.7) diperoleh 2 2 0 1 2 0 1 2 ( ) N y +λy +λ y + =A +λA +λ A + (3.15) atau 2 2 0 1 2 0 1 2 ( ) ( ) ( ) N y +λN y +λ N y + =A +λA+λ A + (3.16) Jika koefisien dari perpangkatan λ dari persamaan (3.16) disamakan pada kedua ruas, maka koefisien dari 0 2

, , ,...

λ λ λ masing-masing memberikan persamaan berikut

0 0 1 1 ( ) ( ) A N y A N y = = 2 ( 2) A =N y (3.17) Jika persamaan (3.14) dan persamaan (3.17) disubstitusikan ke dalam persamaan (3.13), maka diperoleh persamaan berikut

[

]

[

]

[

]

[

] [

]

0 1 0 1 2 2 0 1 2 0 0 1 1 0 1 2 0 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , R y R y L y L y L y R y N y N y N y L h G Ry A Ry A R y R y R y A A G A + + ⎡ ⎤ + + + +_⎢ _⎥+ + ⎣ ⎦ + + + = + − − − − − + + + + + + + + =

dengan L h( )=0 karena h solusi homogen dari persamaan (3.3).

3.3 Aplikasi pada Persamaan Diferensial Abelian

Bentuk umum Persamaan Diferensial Abelian adalah 2 3 0 1 2 3 ' ( ) ( ) ( ) ( ) y = f x +f x y+f x y + f x y . (3.18) Persamaan (3.18) dapat ditulis menjadi

1( ) 2( ) 1( ) 3( ) 2( ) 0( )

Ly− f x y− f x N y − f x N y = f x

(3.19) dengan

(16)

7 d L dx = 2 3 1 2 , ( )N y =y , ( )N y = y . Dalam Metode Dekomposisi Adomian, dimisalkan solusi persamaan diferensial (3.18) dinyatakan dalam bentuk deret berikut

0 ( ) _n( ) n y x y x ∞ = =

∑

, (3.20)

dengan y y y0, 1, 2,... akan ditentukan berikut ini. Bentuk taklinear yang dipilih adalah

2 1( )

N y = y dan 3

2( )

N y =y yang masing-masing memiliki polinomial Adomian sebagai berikut. 1 0 2 0 ( ) , ( ) , n n n n N y A N y B ∞ = ∞ = = =

∑

(3.21) dengan An dan Bn berturut-turut merupakan

uraian polinomial Adomian dari fungsi N1 dan

N2. Berdasarkan persamaan (3.9) diperoleh

empat suku dari polinomial Adomian untuk masing-masing deret An dan Bn sebagai berikut

2 , 0 0 , 1 0 1 2 , 2 0 2 1 , 3 0 3 1 2 2 2 2 2 A y A y y A y y y A y y y y = = = + = + dan 3 , 0 0 2 , 1 0 1 2 2 , 2 0 2 0 1 2 3 . 3 0 3 0 1 2 1 3 3 3 3 6 B y B y y B y y y y B y y y y y y = = = + = + + (3.22) Selanjutnya, jika kedua ruas pada persamaan (3.19) dikenakan operator 1

L− dari kiri, maka diperoleh bentuk

1 2 1 1 1 0 3 2 ( ) ( ) ( ) ( ) ( ) ( ) f x y f x N y y L h L f x f x N y − ⎡ + ⎤ − − _⎢ _⎥= + + ⎣ ⎦ (3.23)

Kemudian persamaan (3.20) dan persamaan (3.21) disubstitusikan ke dalam persamaan (3.23), maka diperoleh bentuk

2 0 1 1 1 0 0 3 0 1 0 ( ) ( ) ( ) ( ) ( ) ( ) n n n n n n n n f x A y x L f x y x L f x B h L f x ∞ ∞ ∞ = − − ∞ = = = − = ⎡ ₊⎤ ⎢ ⎥ ⎢ ⎥ − − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ +

∑

(3.24)

Jika kedua ruas dibandingkan, maka diperoleh 1 0 0 1 1 1 0 2 0 3 0 ( ) ( ( ) ( ) ( ) ) y h L f x y L f x y f x A f x B − − = + = + + 1 2 ( ( )1 1 2( ) 1 3( ) 1) y =L− f x y + f x A +f x B

atau secara umum berbentuk 1 0 0 1 -1 2 -1 1 3 -1 ( ) ( ) ( ) , 1 ( ) n n n n y h L f x f x y f x A y L n f x B − − = + + ⎡ ⎤ = _⎢ _⎥ ≥ + ⎣ ⎦ (3.25) Penurunan persamaan (3.22) dan (3.24) masing-masing dapat dilihat pada Lampiran 4 dan 5.

Dengan demikian solusi Persamaan Diferensial Abelian (3.18) adalah

0 1 2

( ) ( ) ( ) ( )

y x = y x +y x +y x +

dengan y y y0, 1, 2,... diberikan oleh persamaan (3.25), sedangkan Ai dan Bi (i=0,1, 2,…)

diberikan oleh persamaan (3.22).

Untuk memahami metode yang diberikan di atas, maka berikut ini akan diberikan dua contoh kasus. Pada contoh kasus pertama, Metode Dekomposisi Adomian akan dibandingkan dengan metode Runge-Kutta orde empat. Pada contoh kasus kedua, Metode Dekomposisi Adomian akan dibandingkan dengan solusi eksak masalah nilai awal.

Contoh 1: Misalkan diberikan Persamaan Diferensial Abelian berikut

2 2 3

' 4 4 2

y = + xy+ xy +x y ,

(3.26) dengan nilai awal

(0) 0

y = .

Secara analitik solusi masalah nilai awal (3.26) sulit untuk diselesaikan. Oleh karena itu, masalah nilai awal (3.26) akan diselesaikan dengan menggunakan metode numerik.

Berikut ini akan ditentukan solusi hampiran masalah nilai awal (3.26) dengan menggunakan Metode Dekomposisi Adomian yang telah diuraikan sebelumnya. Rumus untuk solusi hampiran dari masalah nilai awal (3.26) yang didasarkan pada persamaan (3.25) adalah

(

)

0 1 2 -1 -1 -1 4 , 4 2 , 1 n n n n y x y L− xy xA x B n = = + + ≥ (3.27) dengan solusi homogen h=0.

Dengan menggunakan aturan rekursif pada persamaan (3.22) diperoleh empat suku

(17)

polinomial Adomian An dan Bn yang

selanjutnya digunakan untuk membentuk solusi y x( ). Empat suku dari solusi ( )y x

atau untuk n=4 diperoleh 0 3 6 4 1 5 6 7 8 9 2 11 4 16 32 8 3 3 64 176 128 112 1664 15 9 7 3 27 512 11 y x x x y x x x x x x y x = = + + = + + + + + 7 8 9 10 3 11 12 13 14 16 256x 1144x 35072x 58592x y 105 45 567 525 81920x 140480x 110336x 297 567 429 295936x 7424x 693 33 = + + + + + + + + 9 10 11 4 12 13 14 15 16 17 18 1024x 36496x 3424384x y 945 1575 31185 11576864x 38692736x 42525 51975 58741120x 48458607616x 43659 30405375 75071168x 23477248x 27027 9639 19678720x 111284224x 11583 = + + + + + + + + + + 19 21 39501 7106560x . 6237 + (3.28) Jadi untuk n=4 diperoleh solusi hampiran masalah nilai awal (3.26) dengan Metode Dekomposisi Adomian sebagai berikut

0 1 2 3 4

( )

y x =y +y +y +y +y .

Untuk suku-suku ke-n dapat dicari berdasarkan aturan rekursif pada persamaan (3.27). Penurunan persamaan (3.27) dan (3.28) masing-masing dapat dilihat pada Lampiran 6 dan 7.

Solusi hampiran masalah nilai awal (3.26) akan ditentukan dengan menggunakan

software MATLAB untuk memperoleh solusi

( )

n

y x untuk nilai n yang berbeda.

Berikut ini diberikan grafik solusi masalah nilai awal (3.26) dengan Metode Dekomposisi Adomian untuk n=5,n=10,

15

n= . Validitas metode ini diperlihatkan dengan membandingkan solusi hampiran dengan metode Runge-Kutta orde empat.

Gambar 3 Perbandingan grafik solusi masalah nilai awal (3.26) dengan metode dekomposisi Adomian untuk n=5 dan metode Runge-Kutta orde empat.

Gambar 4 Perbandingan grafik solusi masalah nilai awal (3.26) dengan metode dekomposisi Adomian untukn=10 dan metode Runge-Kutta orde empat.

Gambar 5 Perbandingan grafik solusi masalah nilai awal (3.26) dengan metode dekomposisi Adomian untukn=15 dan metode Runge-Kutta orde empat. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0 2 4 6 8 10 12 14 metode Runge-Kutta metode dekomposisi Adomian

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0 2 4 6 8 10 12 14 metode Runge-Kutta metode dekomposisi Adomian

(18)

9

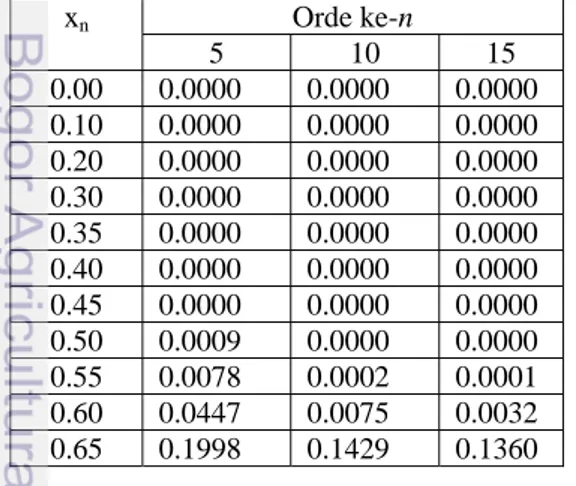
Dari Gambar 3, 4 dan 5 disimpulkan bahwa solusi hampiran dengan Metode Dekomposisi Adomian mendekati solusi dengan Runge-Kutta orde empat dengan ketelitian yang tinggi untuk orde yang makin besar. Ketelitian metode ini pada masalah nilai awal (3.26) diberikan pada Tabel 3.

Tabel 3 Galat hampiran solusi masalah nilai awal (3.26) untuk orde yang berbeda

xn Orde ke-n 5 10 15 0.00 0.0000 0.0000 0.0000 0.10 0.0000 0.0000 0.0000 0.15 0.0000 0.0000 0.0000 0.20 0.0000 0.0000 0.0000 0.25 0.0000 0.0000 0.0000 0.30 0.0001 0.0001 0.0001 0.35 0.0010 0.0010 0.0010 0.40 0.0080 0.0061 0.0061 0.45 0.0271 0.0254 0.0253 0.50 1.4117 0.2816 0.2072 Contoh 2: Misalkan diberikan Persamaan Diferensial Abelian berikut

2 3

' 2 2

y = − + +y y −y

(3.29) dengan nilai awal

(0) 0

y = .

Solusi eksak dari persamaan diferensial (3.29) dengan nilai awal (0)y =0 dinyatakan dalam bentuk implisit berikut

1 1 1 1

ln 1 ln 1 ln 2 ln(2).

2 − −y 6 y+ −3 y− = −x 3

Berikut ini akan ditentukan solusi hampiran masalah nilai awal (3.29) berdasarkan Metode Dekomposisi Adomian yang telah diuraikan sebelumnya. Oleh karena itu, rumus untuk solusi hampiran dari masalah nilai awal (3.29) yang didasarkan pada persamaan (3.25) adalah

(

)

0 -1 -1 -1 -1 -2 2 , 1 n n n n y x y L y A B n = = + − ≥ (3.30) dengan solusi homogen h=0.

Dengan menggunakan aturan rekursif pada persamaan (3.22) diperoleh empat suku polinomial Adomian An dan Bn yang

selanjutnya digunakan untuk membentuk solusi y x( ). Empat suku dari solusi y x( ) atau untuk n=4 diperoleh

3 2 4 1 3 4 5 7 6 2 4 5 6 7 3 8 9 10 5 6 7 8 4 9 0 11 0 1 8 2 3 8 22 24 8 3 3 15 7 22 176 2432 12 15 45 315 517 152 228 35 7 35 26 358 514 60 45 105 315 85499 736 76204 2835 189 1155 5896 y = -2x x y x x x x x x y x x x x x y x x x x x x x y x x x x = − + + = − + − − − = − + − − + + + = − + − − + + − − 12 5896 13 105 455 x − (3.31) Jadi untuk n=4 diperoleh solusi hampiran masalah nilai awal (3.29) dengan Metode Dekomposisi Adomian sebagai berikut

0 1 2 3 4

( )

y x =y +y +y +y +y .

( )

n

Berikut ini diberikan grafik solusi masalah nilai awal (3.29) dengan Metode Dekomposisi Adomian untuk n=5, n=10 dan n=15. Validitas metode ini diperlihatkan dengan membandingkan solusi hampiran dengan Metode Dekomposisi Adomian dan solusi eksak.

Gambar 6 Perbandingan grafik solusi masalah nilai awal (3.29) metode dekomposisi Adomian untuk n=5 dan solusi eksak.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 -1 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1 0 metode Runge-Kutta metode dekomposisi Adomian solusi eksak

(19)

Gambar 7 Perbandingan grafik solusi

masalah nilai awal (3.29) metode dekomposisi Adomian untuk

n=10_{dan solusi eksak.}

Gambar 8 Perbandingan grafik solusi

masalah nilai awal (3.29) metode dekomposisi Adomian untuk

n=15_{dan solusi eksak.}

Dari Gambar 6, 7 dan 8 disimpulkan bahwa solusi hampiran dengan Metode Dekomposisi Adomian mendekati solusi eksak untuk orde yang makin besar. Ketelitian metode ini pada masalah nilai awal (3.29) diberikan pada Tabel 4.

Tabel 4 Galat hampiran solusi masalah nilai awal (3.29) untuk orde yang berbeda

xn Orde ke-n 5 10 15 0.00 0.0000 0.0000 0.0000 0.10 0.0000 0.0000 0.0000 0.20 0.0000 0.0000 0.0000 0.30 0.0000 0.0000 0.0000 0.35 0.0000 0.0000 0.0000 0.40 0.0000 0.0000 0.0000 0.45 0.0000 0.0000 0.0000 0.50 0.0009 0.0000 0.0000 0.55 0.0078 0.0002 0.0001 0.60 0.0447 0.0075 0.0032 0.65 0.1998 0.1429 0.1360

3.4 Aplikasi pada Model Pertumbuhan Populasi Rusa

Persamaan Diferensial Abelian juga muncul dalam pemodelan dari pertumbuhan populasi rusa pada suatu wilayah (Giordano dan Weir 1991). Misalkan Y menyatakan jumlah populasi rusa, maka rata-rata pertumbuhan populasi rusa dalam wilayah tersebut dinyatakan dalam model persamaan berikut ( )( ) dY kY M Y Y m dt = − − (3.32) dengan k menyatakan konstanta pembanding, sedangkan M dan m masing-masing menyatakan jumlah maksimum populasi rusa dan jumlah minimum populasi rusa.

Berikut ini ilustrasi mengenai pemakaian Metode Dekomposisi Adomian untuk menyelesaikan model yang diberikan pada persamaan (3.32). Berdasarkan persamaan (3.32) , model matematika untuk pertumbuhan populasi rusa dalam wilayah tersebut adalah

2 3

' 35 5.35 0.05

y = − y+ y − y . (3.33) Asumsikan pada awal pengamatan terdapat 50 ekor rusa sehingga diperoleh nilai awal berikut

(0) 50

y = .

Berikut ini akan ditentukan solusi hampiran masalah nilai awal (3.33) berdasarkan Metode Dekomposisi Adomian yang telah diuraikan sebelumnya. Oleh karena itu, rumus untuk solusi hampiran dari masalah nilai awal (3.33) yang didasarkan pada persamaan (3.25) adalah

0 1 1 1 1 50 ( 35 5.35 0.05 ), 1 n n n n y y L− y− A− B− n = = − + − ≥ (3.34) dengan solusi homogen h=0.

Dengan menggunakan aturan rekursif pada persamaan (3.22) diperoleh empat suku polinomial Adomian An dan Bn yang

selanjutnya digunakan untuk membentuk solusi y x( ). Empat suku n = 4 dari solusi

( ) y x adalah 0 1 2 2 6 3 3 9 4 4 50 5375 335938 6.70755x10 4.09179x10 . y y t y t y t y t = = = = − = − (3.35) 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 -1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 metode Runge-Kutta metode dekomposisi Adomian solusi eksak 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 -1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 metode Runge-Kutta metode dekomposisi Adomian solusi eksak

(20)

11

Jadi untuk n=4 diperoleh solusi hampiran masalah nilai awal (3.33) dengan Metode Dekomposisi Adomian sebagai berikut

0 1 2 3 4

( )

y x =y +y +y +y +y .

( )

n

Berikut ini diberikan grafik solusi masalah nilai awal (3.33) dengan Metode Dekomposisi Adomian untuk n=5,n=10 dan n=15. Validitas metode ini diperlihatkan dengan membandingkan solusi hampiran dengan Metode Dekomposisi Adomian dan solusi eksak.

Gambar 9 Perbandingan grafik solusi masalah nilai awal (3.33) metode dekomposisi Adomian dan solusi numerik. Simbol: blue;solusi numerik: red_;n=5: yellow_; n=10:green;n=15

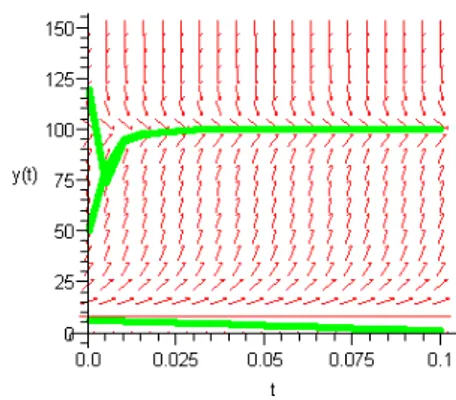
Dari Gambar 9 disimpulkan bahwa solusi hampiran dengan Metode Dekomposisi Adomian mendekati solusi numerik untuk orde yang makin besar. Gambar 10 berikut ini menunjukkan bidang fase pertumbuhan populasi rusa berdasarkan model matematika pada persamaan (3.33).

Gambar 10 Bidang fase pertumbuhan populasi rusa dengan M = 100 dan m = 7.

Berdasarkan Gambar 10 disimpulkan bahwa populasi rusa akan mengalami kepunahan, jika populasi rusa berada di bawah jumlah m = 7. Jika populasi rusa berada di antara 7≤y t( ) 100≤ , maka populasi rusa akan mengalami peningkatan hingga jumlah 100. Jika populasi rusa berada di atas 100,

maka populasi rusa akan menurun kemudian meningkat hingga mencapai jumlah 100. 0.0000 0.005 0.010 0.015 0.020 20 40 60 80 100 120 140 waktu pop ul as i rus a

(21)

IV KESIMPULAN

Metode Dekomposisi Adomian yang dikaji

pada tulisan ini dapat digunakan untuk mendekati solusi hampiran dari Persamaan Diferensial Abelian. Dari beberapa contoh yang telah diuraikan ditunjukkan bahwa persamaan diferensial yang diselesaikan dengan menggunakan Metode Dekomposisi Adomian memberikan solusi yang mendekati solusi eksak maupun solusi numerik yang salah satunya diperoleh dengan menggunakan metode Runge-Kutta orde empat. Beberapa contoh numerik telah disajikan untuk mengilustrasikan ketelitian dari Metode Dekomposisi Adomian. Metode ini merupakan metode yang cocok digunakan dalam mendekati solusi eksak dari setiap persamaan diferensial.

Hal lain yang merupakan keuntungan Metode Dekomposisi Adomian adalah kekonvergenan yang dapat tercapai untuk orde

yang makin tinggi yang dinyatakan dalam rangkaian solusi deret. Solusi dari Metode Dekomposisi Adomian yang diperoleh dapat diterapkan untuk berbagai jenis persamaan diferensial biasa baik yang linear maupun taklinear.

Berdasarkan contoh kasus pada pertumbuhan populasi rusa yang diselesaikan dengan Metode Dekomposisi Adomian dan bidang fase disimpulkan bahwa populasi rusa akan mengalami kepunahan jika populasi rusa berada di bawah jumlah minimum. Populasi rusa akan mengalami peningkatan yang kontinu jika berada di antara selang jumlah minimum dan maksimum. Kemudian, jika populasi rusa berada di atas jumlah maksimum, maka populasi rusa akan menurun kemudian meningkat kembali hingga mencapai jumlah maksimum.

DAFTAR PUSTAKA

Abbaoui K, Cherruault Y. 1996. New Ideas

for Proving Convergence of Decomposition Method. Jurnal of Applied

29(7):103-108.

Adomian G. 1988. A Review of the Decomposition Method in Applied Mathematics. Jurnal of Applied

135(2):501-544.

Adomian G. 1994. Solving Frontier Problems of Physics the Decomposition Method.

Kluwer Academic.

Braun M. 1993. Differential Equation and

Their Applications. Ed ke-4. New York:

Springer.

Cherruault Y. 1989. Convergences of Adomian’s Method. Math 18(2):31-38. Cherruault Y, Adomian G. 1993.

Decomposition Methods: A New Proof of Convergence. Math 18(12):103-106.

Farlow SJ. 1994. An Introduction to Differential Equations and Their

Applications. Singapore: McGraw-Hill.

Giordano FR, Weir MD. 1991. Differential

Equations a Modeling Approach.

Addison-Wesley Pub Co.

Jaradat OK. 2008. Adomian Decomposition Method for solving Abelian Differential Equation. Jurnal of Applied 8(10):1962-1966.

Sahid. 2005. Pengantar Komputasi Numerik

dengan MATLAB. ANDI Yogyakarta.

Seng et al. 1996. Adomian’s Polinomials for Nonlinear Operators. Math 24(1):59-65. Wazwaz AM. 2002. Partial Differential

Equation Method and Applications.

Netherland: Balkema.

Zwillinger D. 1992. Handbook of Differential

Equation. Second edition. Ed ke-2. San

(22)

13

(23)

Lampiran 1 Penurunan persamaan (2.10)

Tinjau persamaan (2.9) yang ditulis kembali sebagai berikut: 2 ' 2

y = xy+xy

atau dapat juga ditulis menjadi persamaan berikut

' ( 2)

y =xy y+

dan nilai awal (0)y =1.

Solusi eksak masalah nilai awal (2.9) dapat diselesaikan dengan metode pemisahan variabel yang telah dikaji sebelumnya. Berikut ini merupakan penurunan persamaan masalah nilai awal (2.9) dalam memperoleh solusi eksak.

Dari ' ( 2) y =xy y+ atau ( 2) dy xy y dx = + diperoleh ( 2) dy xdx y y+ =

∫

atau 1 1 1 1 2

∫

ydy−2

∫

y+2dy=

∫

xdx atau 2 1 1 1 ln ln( 2) 2 y−2 y+ =2x +c atau 2 1 ln 2 2 y x c y ⎛ ⎞ = + ⎜ ⎟ ⎜ ₊ ⎟ ⎝ ⎠ atau 2 1 2 2 x y Ae y+ = .

Jika nilai awal (0)y =1 disubstitusikan ke dalam persamaan terakhir di atas, maka diperoleh 1 3 3 A= , sehingga diperoleh 2 1 2 1 3 2 3 x y e y+ = atau 2 1 2 3 x y e y+ = .

Dengan demikian solusi masalah nilai awal (2.9) adalah

2 2 2 ( ) 3 x x e y x e = − .

(24)

15

Lampiran 2 Penurunan Persamaan (3.8)

Misalkan bentuk taklinear N y( ) dinyatakan dalam fungsi ( )f y berupa fungsi polinomial berikut 0

( )

n _n n

f y

λ

A

∞ =

=

∑

_dengan 0 1 ! n n n d A Ny n dλ _λ₌ = . (6.1) Fungsi f diasumsikan analitik terhadap λ sehingga f dapat diturunkan hingga n kali terhadap λ_. Dari definisi N y( )= f y( ), maka persamaan (6.1) dapat ditulis menjadi

0 1 ( ( )) ! n n n d A f y n dλ λ _λ₌ = . (6.2) Jika dinotasikan D d dλ

= , maka persamaan (6.2) menjadi

(

)

₀ 1 ! n n A D f n λ= = (6.3) dimana n

D f notasi untuk turunan ke-n dari f terhadap λ.

Dengan menggunakan aturan rantai, maka persamaan (6.3) memberikan 1 1 1 0 2 2 2 2 2 2 2 2 1 0 2 0 3 3 3 2 2 3 3 1 3 3 2 2 3 0 1 2 0 3 0 '( ) 1 1 1 1 ''( ) '( ) 2 2 2 2 1 1 3 '''( ) ''( ) '( ) 3! 3! 3! . f y A D f y f y y f y f y A D f y f y y f y y y y f y f y y f y A D f f y y y f y y f y y y y λ λ λ λ λ λ λ ∂ ∂ = = = ∂ ∂ ∂ ⎛∂ ⎞ ∂ ∂ = = _⎜ _⎟ + = + ∂ ∂ ∂ ⎝ ⎠ ∂ ⎛_∂ _⎛_∂ _⎞ _∂ _{∂ ∂} _{∂ ∂} ⎞ = = ⎜_⎜ _⎜ _⎟ + + ⎟_⎟= + + ∂ ∂ ∂ ∂ ⎝ ⎠ ∂ ∂ ∂ ⎝ ⎠

Lampiran 3 Penurunan persamaan (3.11) Jika ruas kanan persamaan (3.10) berikut ini

(

)

(

)

2 1 1 2 1 2

0 1 2 0 1 2 ( 0 1 2 )

y +λy +λ y + = +h L G− −λL− R y +λy +λ y + −λL− A +λA+λ A +

diuraikan, maka diperoleh

(

)

(

)

(

) (

)

(

) (

)

1 1 1 0 0 1 1 2 1 2 0 1 2 0 1 2 1 1 2 1 3 1 1 2 1 3 1 0 1 2 0 1 2 1 1 1 2 1 1 0 0 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

n _n n _n n n h L G L R y L A h L G L R y y y L A A A h L G L Ry L Ry L Ry L A L A L A h L G L Ry L A L Ry L A λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ ∞ ∞ − − − = = − − − − − − − − − − − − − − − + − − = + − + + + − + + + = + − + + + − + + + = + − + − + −

∑

(

)

3 1 1 2 2 ( ) ( ) L− Ry +L− A −

(25)

Selanjutnya, koefisien dari pangkat

λ

yang sama pada kedua ruas dibandingkan, diperoleh 1 0 1 1 1 0 0 1 1 2 1 1 1 1 3 2 2 ( ) ( ) ( ) ( ) ( ) ( ) . y h L G y L Ry L A y L Ry L A y L Ry L A − − − − − − − = + = − − = − − = − −

Lampiran 4 Penurunan persamaan (3.22) Berdasarkan persamaan (3.21) berikut

2 1 0 ( ) _n n N y y A ∞ = = =

∑

, 2 3 0 ( ) _n, n N y y B ∞ = = =

∑

dan persamaan (3.8) berikut

0 0 1 1 0 2 1 2 2 0 0 3 1 3 3 0 1 2 0 0 ( ) '( ) '( ) ''( ) 2 '( ) ''( ) '''( ) 3! A f y A y f y y A y f y f y y A y f y y y f y f y = = = + = + +

maka berikut ini, empat suku polinomial Adomian untuk masing-masing nilai An dan Bn , adalah 2 0 0 0 0 1 1 0 1 0 0 1 2 2 2 2 1 1 1 2 2 0 0 2 0 0 0 2 0 2 1 3 3 1 1 3 3 0 1 2 0 0 3 0 1 2 0 0 0 3 1 2 ( ) ( ) '( ) '( ) 2 '( ) ''( ) '( ) ''( ) 2 2 2 2! 2! 2! '( ) ''( ) '''( ) '( ) ''( ) '''( ) 2 2 3! 3! A f y N y y A y f y y N y y y y y y A y f y f y y N y N y y y y y y y y A y f y y y f y f y y N y y y N y N y y y y y = = = = = = = + = + = + = + = + + = + + = + 3 0 0 0 0 2 1 1 0 1 0 0 1 2 2 2 2 2 2 1 1 1 2 2 0 0 2 0 0 0 2 0 0 2 0 1 3 3 1 1 3 3 0 1 2 0 0 3 0 1 2 0 0 ( ) ( ) '( ) '( ) 3 '( ) ''( ) '( ) ''( ) 3 (6 ) 3 3 2! 2! 2! '( ) ''( ) '''( ) '( ) ''( ) '''( ) 3! 3! B f y N y y B y f y y N y y y y y y B y f y f y y N y N y y y y y y y y y y B y f y y y f y f y y N y y y N y N y = = = = = = = + = + = + = + = + + = + + = 2 13 2 3 0 3 0 1 2 0 3 0 1 2 1 3 6 6 3 6 . 3! y y y + y y y + = y y + y y y +y

Lampiran 5 Penurunan persamaan (3.24) Tinjau persamaan (3.19) berikut

0( ) 1( ) 2( ) 1( ) 3( ) 2( )

Ly= f x +f x y+f x N y +f x N y

dan persamaan (3.23) berikut

1 1 1 1

0 1 2 1 3 2

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

(26)

17

Jika y x( ) pada persamaan (3.20) dan N y₁( ), ( )N₂ y pada persamaan (3.21) disubstitusikan ke dalam persamaan (3.23), maka diperoleh

1 1 1 1 0 1 2 3 0 0 0 0 1 1 1 0 1 2 3 0 0 0

( )

n n n n n n n n n n n n n n

y x

c

L f x

y x

L f x

A

L f x

B

c

L f x

y x

L

f x

A

f x

B

∞ ∞ ∞ ∞ − − − − = = = = ∞ ∞ ∞ − − − = = =

= +

+

⎡

⎤

= +

+

_⎢

+

_⎥

⎣

⎦

∑

.

Lampiran 6 Penurunan persamaan (3.27) Jika Persamaan Diferensial Abelian (3.18) berikut

2 3

0 1 2 3

' ( ) ( ) ( ) ( )

y = f x +f x y+f x y + f x y ,

dibandingkan dengan persamaan diferensial (3.26) berikut 2 2 3

' 4 4 2

y = + xy+ xy +x y ,

maka diperoleh bentukf x0( )=4; ( )f x1 =4 ; ( )x f x2 =2 ; ( )x f x3 =x2. Berdasarkan persamaan (3.25) berikut

1 0 0 1 1 1 2 1 3 1 ( ) ( ( ) ( ) ( ) ), 1 n n n n y c L f x y L f x y f x A f x B n − − − − − = + = + + ≥ diperoleh

(

)

0 1 2 -1 -1 -1 4 , 4 2 , 1 n n n n y x y L− xy xA x B n = = + + ≥ . Lampiran 7 Penurunan persamaan (3.28)

Software Mathematica 6 digunakan untuk memperoleh solusi hampiran persamaan (3.26)

secara numerik. Berikut ini diberikan perintah untuk menentukan suku-suku ynyang merupakan

solusi dari persamaan diferensial (3.26) dengan menggunakan Metode Dekomposisi Adomian. Dalam metode ini telah diperoleh persamaan (3.27) berikut

(

)

0 1 2 -1 -1 -1 4 , 4 2 , 1 n n n n y x y L− xy xA x B n = = + + ≥

dengan An, Bn pada persamaan (3.22) yang merupakan suku-suku polinomial Adomian yang akan

digunakan dalam menyusun syntax berikut ini.

Syntax Mathematica 6 In[1] y0:=4*x In[2] y1=Integrate[4*x*y0+2*x*y02 +x2 *y03 ,x] Out[2] (16*x3)/3+8*x4+(32*x6)/3

In[3] y2=Integrate[4*x*y1+2*x*2*y0*y1+x2*3*y02*y1,x]

Out[3](64*x5)/15+(176*x6)/9+(128*x7)/7+(112*x8)/3+(1664*x9)/27+(51* x11)/11 In[4] y3=Integrate[4*x*y2+2*x*(y12 +2*y0*y2)+x2 *(3*y0*y12 +3*y02 *y2),x] Out[4](256*x7)/105+(1144*x8)/45+(35072*x9)/567+(58592*x10)/525+(819 20*x11)/297+(140480*x12)/567+(110336*x13)/429+(295936*x14)/693+(742 4*x16)/33

In[5]y4=Integrate[4*x*y3+2*x*(2*y1*y2+2*y0*y3)+x2*(y13+6*y0*y1*y2+3 y02*y3),x] Out[5](1024x9)/945+(36496*x10)/1575+(3424384*x11)/31185+(11576864* x12)/42525+(38692736*x13)/51975+(58741120*x14)/43659+(48458607616* x15)/30405375+(75071168*x16)/27027+(23477248*x17)/9639+(19678720*x1 8 )/11583+(111284224*x19)/39501+(7106560*x21)/6237

(27)

Langkah di atas dapat dilanjutkan untuk menentukan y_n, 6n≥ .

Lampiran 8 Syntax MATLAB 7.0.1 untuk menyelesaikan Contoh 1 Untuk menyelesaikan masalah pada Contoh 1, dimisalkan:

0 0

0.5 0.01 0 0

n

x = h= x = y = .

Berikut ini syntax MATLAB 7.0.1 untuk menyelesaikan Contoh 1. xn=0.5; h=0.01; x0=0; y0=0; h0=0; yh=[x0 y0]; for k=1(xn/h); x=x0+h; s1=4+(4*x0*y0)+(2*x0*(y0^2))+((x0^2)*(y0^3)); s2=4+(4*(x0+(h/2))*(y0+h*s1/2))+(2*(x0+h/2)*((y0+h*s1/2)^2))+( ((x0+h/2)^2)*((y0+h*s1/2)^3)); s3=4+(4*(x0+h/2)*(y0+h*s2/2))+(2*(x0+h/2)*((y0+h*s2/2)^2))+((( x0+h/2)^2)*((y0+h*s2/2)^3)); s4=4+(4*x*(y0+h*s3))+(2*(x)*((y0+h*s3)^2))+((x.^2)*((y0+h*s3)^ 3)); y=y0+h*(s1+2*(s2+s3)+s4)/6; yh=[yh;x y]; x0=x;y0=y; end yh a=yh(,1); b=yh(,2); plot(a,b) hold on x=0;0.01;0.5; plot(x,4*x+(16*x.^3)/3+8*x.^4+(32*x.^6)/3+(64*x.^5)/15+(176*x.^6)/ 9+(128*x.^7)/7+(112*x.^8)/3+(1664*x.^9)/27+(512*x.^11)/11+(256* x.^7)/105+(1144*x.^8)/45+(35072*x.^9)/567+(58592*x.^10)/525+(81 920*x.^11)/297+(140480*x.^12)/567+(110336*x.^13)/429+(295936*x. ^14)/693+(7424*x.^16)/33+(1024*x.^9)/945+(36496*x.^10)/1575+(34 24384*x.^11)/31185+(11576864*x.^12)/42525+(38692736*x.^13)/5197 5+(58741120*x.^14)/43659+(48458607616*x.^15)/30405375+(75071168 *x.^14)/27027+(23477248*x.^17)/9639+(19678720*x.^18)/11583+(111 28422*x.^19)/39501+(7106560*x.^21)/6237,'--') hold off .

Lampiran 9 Penurunan persamaan (3.30) Jika Persamaan Diferensial Abelian (3.18) berikut

(28)

19

2 3

0 1 2 3

' ( ) ( ) ( ) ( )

y = f x +f x y+f x y + f x y ,

dibandingkan dengan persamaan diferensial (3.29) berikut 2 3

' 2 2

y = − + +y y −y

maka diperoleh bentuk f x0( )= −2; ( )f x1 =1; ( )f x2 =2; ( )f x3 = −1. Berdasarkan persamaan (3.25) berikut

1 0 0 1 1 1 2 1 3 1 ( ) ( ( ) ( ) ( ) ), n 1 n n n n y c L f x y L f x y f x A f x B − − − − − = + = + + ≥ diperoleh

(

)

0 1 -1 1 -1 2 , 2 , 1 n n n n y x y L− y A− B n = − = + − ≥ .

Lampiran 10 Penurunan persamaan (3.31)

Software Mathematica 6 digunakan untuk memperoleh solusi hampiran persamaan (3.29)

secara numerik. Berikut ini diberikan perintah untuk menentukan suku-suku ynyang merupakan

solusi dari persamaan diferensial (3.29) dengan menggunakan Metode Dekomposisi Adomian. Dalam metode ini telah diperoleh persamaan (3.30) berikut

(

)

0 1 -1 1 -1 2 , 2 , 1 n n n n y x y L− y A₋ B n = − = + − ≥

dengan A_n, B_n pada persamaan (3.22) yang merupakan suku-suku polinomial Adomian yang akan digunakan dalam menyusun syntax berikut ini.

Syntax Mathematica 6 In [1] y0:=-2 x In [2] y1=Integrate[y0+2y02-y03,x] Out [2] -x2+(8x3)/3+2x4 In [3] y2=Integrate[y1+4y0*y1-3y02_*y1,x] Out [3] -(x3/3)+(8 x4)/3-(22 x5)/15-8 x6-(24 x7)/7 In [4] y3=Integrate[y2+2(y12_{+2y0*y2)-(3y0*y1}2_+3y02_*y2),x]

Out [4] -(x4/12)+(22*x5)/15-(176x6)/45-(2432x7)/315+(517

x8)/35+(152x9)/7+(228x10)/35

In [5] y4=Integrate[y3+2*(2y1*y2+2y0*y3)-(y13_{+6y0*y1*y2+3y0}2_y3),x] Out [5] -(x5/60)+(26x6)/45-(358x7

)/105-(514x8)/315+(85499x9)/2835+(736x10)/189-(76204x11

)/1155-(5896x12)/105-(5896x13)/455

Langkah di atas dapat dilanjutkan untuk menentukan yn, 6n≥ .

Lampiran 11 Syntax MATLAB 7.0.1 untuk menyelesaikan Contoh 2 Untuk menyelesaikan masalah pada Contoh 2, dimisalkan:

(29)

0 0 0.5 0.01 0 0

n

x = h= x = y = .

Berikut ini syntax MATLAB 7.0.1 untuk menyelesaikan Contoh 2. xn=.5; h=0.01; x0=0; y0=0; h0=0; yh=[x0 y0]; for k=1(xn/h); x=x0+h; s1=-2+y0+2*y0^2-y0^3; s2=-2+(y0+h*s1/2)+2*((y0+h*s1/2)^2)-((y0+h*s1/2)^3); s3=-2+(y0+h*s2/2)+2*((y0+h*s2/2)^2)-((y0+h*s2/2)^3); s4=-2+(y0+h*s3)+2*((y0+h*s3)^2)-((y0+h*s3)^3); y=y0+h*(s1+2*(s2+s3)+s4)/6; yh=[yh;x y]; x0=x;y0=y; end yh a=yh(,1); b=yh(,2); plot(a,b,'LineWidth',2) hold on x=0;0.01;0.5; zz1=-2*x-x.^2+(8*x.^3)/3+2*x.^4 -(x.^3/3)+(8*x.^4)/3-(22*x.^5)/15-8*x.^6-(24*x.^7)/7 (x.^4/12)+(22*x.^5)/15(176*x.^6)/45(2432*x.^7)/315+(517*x.^8)/35+(152*x.^9)/7+(228*x.^10)/35 - (x.^5)/60+(26*x.^6)/45-(358*x.^7)/105- (514*x.^8)/315+(85499*x.^9)/2835+(736*x.^10)/189- (76204*x.^11)/1155-(5896*x.^12)/105-(5896*x.^13)/455-(x.^6)/360+(19*x.^7)/105- (325*x.^8)/168+(956*x.^9)/405+(767219*x.^10)/28350- (6986996*x.^11)/155925-(1981766*x.^12)/17325+(3428384*x.^13)/45045+ (24790124*x.^14)/105105+(449632*x.^15)/3185+(84306*x.^16)/318 5-(x.^7/2520)+x.^8/21-(19069*x.^9)/22680+(656959*x.^10)/226800+ (4528343*x.^11)/311850-(148980349*x.^12)/2138400-(5449942319*x.^13)/97297200+(36740087191*x.^14)/123832800+ (1427236030963*x.^15)/3714984000- (46560965233*x.^16)/181621440- (61082763354017*x.^17)/43418875500-(269974232947049*x.^18)/183891708000+ (9146583579348703*x.^19)/6599669076000+(36411299402681503*x.^ 20)/7815397590000+(178834409096246053*x.^21)/207889575894000- (10389706988415274673*x.^22)/816709048155000-(641794439427834289*x.^23)/39845502046350+ (114601346378525530666*x.^24)/6431583754220625+(2754699879021 9617878219*x.^25)/547875653137312500+ (2714746056286447622203*x.^26)/2564058056682622500-(2659104484473794492516891*x.^27)/33283445928091734375- (1982016775878415623281107*x.^28)/37392513326621578125+(31456 17986948001314830303*x.^29)/61964736369830043750+(14643019613 567092168841414*x.^30)/186962566633107890625+(149058969898197 09730543096*x.^31)/747019321791839971875-