Skripsi. Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika. Oleh:

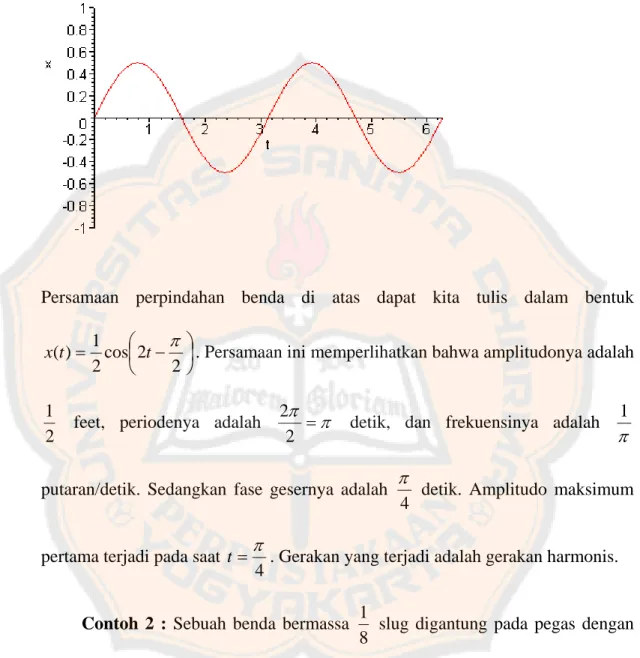
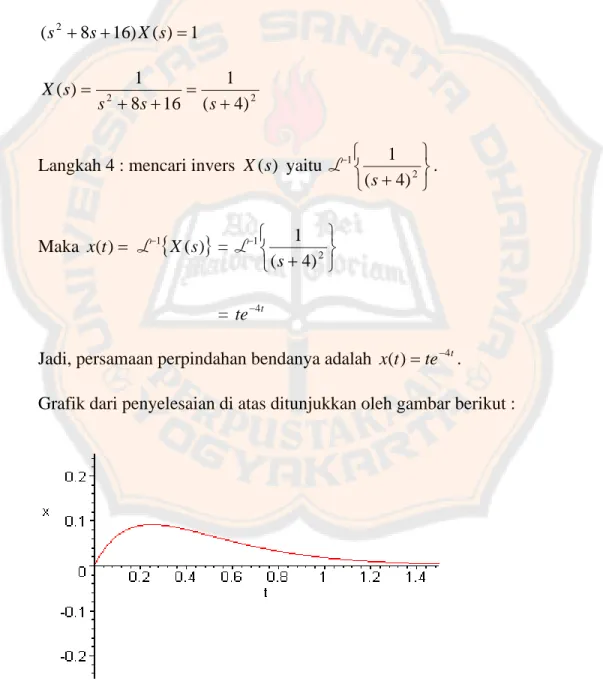
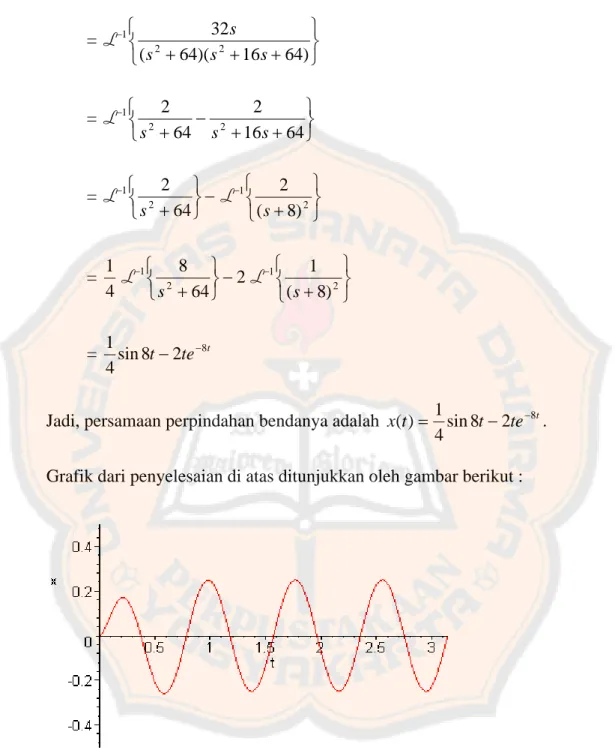
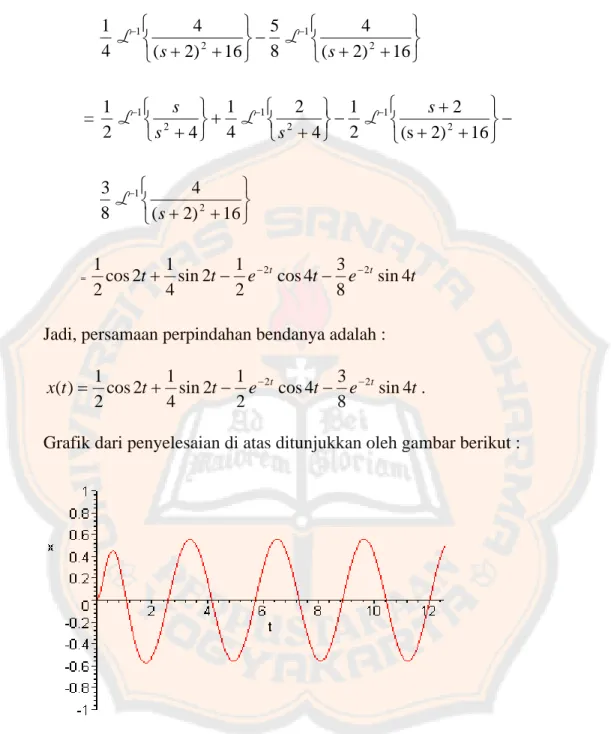
i

TRANSFORM LAPLACE DAN PENERAPANNYA DALAM

PENYELESAIAN MASALAH NILAI AWAL PERSAMAAN DIFERENSIAL LINEAR ORDE DUA DENGAN KOEFISIEN KONSTAN

KHUSUSNYA PADA GETARAN PEGAS

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh:

Marselina Kartika NIM. 031414028

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

iv

HALAMAN PERSEMBAHAN

“…, berdirilah teguh, jangan goyah, dan giatlah selalu dalam pekerjaan Tuhan! Sebab kamu tahu, bahwa dalam persekutuan dengan Tuhan

jerih payahmu tidak sia-sia.” (1 Korintus 15:58)

“ Pengalaman membuat engkau mampu untuk mengenal sebuah kesalahan bilamana engkau melakukannya lagi “

(Franklin P. Jones)

“ Jangan sekali-kali putus asa, tapi jika engkau putus asa juga, teruslah bekerja dalam keputusasaan itu “

(Edmund Barke)

Dengan penuh kasih aku persembahkan karya mungilku ini untuk : Tuhan Yesus dan Bunda Maria Papa, Mama, dan Adikku tersayang yang selalu menjadi penyemangatku Segenap keluarga di Bangka dan di Jawa Rekan-rekan mahasiswa/i PMAT ’03 dan sahabat-sahabatku Almamaterku,Universitas Sanata Dharma

vi

ABSTRAK

Ada berbagai metode yang dapat digunakan untuk menentukan penyelesaian masalah nilai awal dari suatu persamaan diferensial. Salah satunya adalah metode transform Laplace. Transform Laplace dari suatu fungsi f(t) adalah fungsi F(s) yang dinyatakan oleh L

{ }

∫

∞ − = = 0 ) ( ) ( ) (t F s e f t dt f st . Jika L

{ }

f(t) =F(s) maka f(t) disebut invers transform Laplace dari F(s) dan secara simbolis ditulis

=

) (t

f L−1

{

F(s)

}

.

Langkah-langkah untuk menyelesaikan masalah nilai awal persamaan diferensial linear orde dua dengan koefisien konstan yaitu dengan mengambil transform Laplace dari kedua ruas persamaan diferensial. Dengan menggunakan sifat linearitas transform Laplace, teorema transform Laplace dari turunan, dan kondisi awal yang diberikan akan diperoleh persamaan aljabar dalam s. Kemudian kita selesaikan persamaan aljabar tersebut. Selanjutnya untuk menentukan penyelesaian masalah nilai awal adalah dengan menggunakan invers transform Laplace.

Persamaan diferensial linear orde dua dengan koefisien konstan mempunyai penerapan pada getaran pegas. Dalam penerapan ini, untuk mendapatkan persamaan diferensial linear orde dua dengan koefisien konstan dari getaran pegas tersebut kita terapkan hukum Hooke dan hukum Newton II. Untuk menentukan persamaan perpindahan benda dari getaran pegas dapat digunakan metode transform Laplace dengan langkah-langkah yang sama seperti yang dikemukakan di atas.

vii

ABSTRACT

There are some methods that can be used to determine the solution of the initial value problem of a differential equation. One of them is the Laplace transform method. Laplace transform of function f(t) is function F(s) stated by

L

{ }

∫

∞ − = = 0 ) ( ) ( ) (t F s e f t dt

f st . If L

{ }

f(t) =F(s) then f(t) is called the inverse Laplace transform of F(s) and symbolically it is written f(t)=L−1

{

F(s)

}

.

Steps for solving the initial value problem of a second order linear differential equation with constant coefficients are obtained by taking the Laplace transform of both sides of the differential equation. By using the linear property of the Laplace transform, the theorem of the Laplace transform of derivatives and the initial condition that is given, we will get an algebraic equation in s. Then we solve the algebraic equation. Next, to determine the solution of the initial value problem we use the inverse Laplace transform.

Second order linear differential equation with constant coefficients have an application in spring vibration. In this application, in order to get a second order linear differential equation with constant coefficients of the spring vibration we apply the Hooke law and the second Newton law. To determine the equation for the object displacement in the spring vibration, we can use the Laplace transform method with the same steps as mentioned above.

viii

KATA PENGANTAR

Puji dan syukur ke hadirat Allah Bapa di Surga karena penulis dapat menyelesaikan skripsi dengan judul “Transform Laplace dan Penerapannya dalam Penyelesaian Masalah Nilai Awal Persamaan Diferensial Linear Orde Dua dengan Koefisien Konstan Khususnya pada Getaran Pegas”. Skripsi ini penulis susun untuk memenuhi salah satu syarat memperoleh gelar Sarjana Pendidikan pada Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan di Universitas Sanata Dharma Yogyakarta.

Selama penyusunan skripsi ini banyak kesulitan dan hambatan yang penulis alami. Namun dengan bantuan berbagai pihak semua kesulitan dan hambatan tersebut dapat teratasi. Untuk itu, dalam kesempatan ini penulis dengan tulus hati ingin mengucapkan terima kasih yang tak terhingga kepada :

1. Tuhan Yesus dan Bunda Maria yang selalu menjaga, melindungi, dan menuntun langkahku. Puji syukur atas segala berkat dan anugerah yang telah kuterima. 2. Bapak Drs. A. Tutoyo, M.Sc. selaku dosen pembimbing yang telah membimbing,

mengarahkan dengan sabar, menyediakan waktu, dan memberikan masukan serta kritikan yang berharga kepada penulis selama proses penyusunan skripsi ini. 3. Bapak Dr. St. Suwarsono selaku Ketua Program Studi Pendidikan Matematika

ix

menempuh kuliah serta atas masukan dan kritikan yang bermanfaat untuk penyempurnaan skripsi ini.

4. Bapak Drs. Al. Haryono selaku Dosen Pembimbing Akademik angkatan 2003 dan selaku dosen penguji yang selalu membimbing dan memberikan kemudahan-kemudahan selama penulis menempuh kuliah serta atas masukan dan kritikan yang bermanfaat untuk penyempurnaan skripsi ini.

5. Segenap dosen JPMIPA, khususnya dosen-dosen Program Studi Pendidikan Matematika, Universitas Sanata Dharma yang telah mendidik, membagi pengetahuan dan pengalaman yang sangat bermanfaat kepada penulis.

6. Bapak Sunardjo dan Bapak Sugeng di sekretariat JPMIPA atas segala keramahan, bantuan, dan kerja samanya dalam membantu penulis selama kuliah hingga penyelesaian skripsi ini.

7. Papa Venantius Widiyanto, Mama Petronella Ratnawati, dan adikku tersayang Benediktus Raditya atas doa yang tak pernah kunjung henti, cinta, kasih sayang, perhatian, kesempatan, nasehat, dan dorongan yang diberikan baik secara materiil maupun spiritual. Kalian adalah semangatku untuk menyelesaikan skripsi ini. Semoga skripsiku ini dapat menjadi hadiah kecil yang membanggakan.

8. Sahabat terbaikku, Mbak Wr, Era, dan Heni yang selalu jadi tempat curhatku, terima kasih atas bantuan, semangat, perhatian, masukan, dan kritikan yang sangat berarti. Teman yang baik tidak selalu memberi ciuman dan pelukan tapi terkadang juga tamparan agar aku sadar dan bangkit dari kesalahan. Terima kasih untuk persahabatan kita.

xi

DAFTAR ISI

Halaman

HALAMAN JUDUL i

HALAMAN PERSETUJUAN PEMBIMBING ii

HALAMAN PENGESAHAN iii

HALAMAN PERSEMBAHAN iv

PERNYATAAN KEASLIAN KARYA v

ABSTRAK vi

ABSTRACT vii

KATA PENGANTAR viii

DAFTAR ISI xi BAB I PENDAHULUAN 1 A. Latar Belakang 1 B. Rumusan Masalah 7 C. Batasan Masalah 7 D. Tujuan Penulisan 8 E. Metode Penulisan 8 F. Sistematika Penulisan 8

BAB II TRANSFORM LAPLACE 10

A. Pengertian Transform Laplace 10

B. Sifat-Sifat Transform Laplace 22

C. Invers Transform Laplace 26

D. Transform Laplace dari Turunan dan Integral 29

E. Konvolusi Dua Fungsi f(t) dan g(t) 34

F. Aplikasi Transform Laplace dalam Menyelesaikan Masalah Nilai Awal Persamaan Diferensial Linear Orde Dua dengan Koefisien Konstan 40

xii

BAB III PENERAPAN TRANSFORM LAPLACE DALAM

PENYELESAIAN MASALAH NILAI AWAL PERSAMAAN DIFERENSIAL LINEAR ORDE DUA DENGAN KOEFISIEN

KONSTAN PADA GETARAN PEGAS 60

A. Getaran Tak Teredam 63

B. Getaran Teredam 70

C. Getaran Terpaksa Tak Teredam 79

D. Getaran Terpaksa Teredam 88

BAB IV PENUTUP 100

DAFTAR PUSTAKA 102

1

BAB I

PENDAHULUAN

A. Latar Belakang

Persamaan diferensial adalah persamaan yang memuat derivatif atau diferensial dari satu atau lebih fungsi. Persamaan diferensial dapat diklasifikasikan dengan banyak cara. Jika fungsi yang belum diketahui dalam persamaan diferensial bergantung hanya pada satu variabel bebas maka persamaan itu disebut persamaan diferensial biasa. Bentuk umum persamaan diferensial biasa : 0 ) ,..., , , , , ( ₃ 3 2 2 = n n dx y d dx y d dx y d dx dy y x f ,

dengan x menyatakan variabel bebas dan y menyatakan variabel tak bebas. Sedangkan jika fungsi yang belum diketahui bergantung pada dua atau lebih variabel bebas, maka persamaan itu disebut persamaan diferensial parsial. Bentuk umum persamaan diferensial parsial :

0 ) ,..., , , , , , , , ( ₂ 2 2 2 2 = ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ n n y z y z y x z x z y z x z z y x f ,

dengan x dan y menyatakan variabel bebas, sedangkan z menyatakan variabel tak bebas. Contoh persamaan diferensial :

xy dx dy

2

0 2 3 2 2 2 + − = y dx dy x dx y d x (2) 0 = ∂ ∂ + ∂ ∂ y u x u (3) x x u t u + = ∂ ∂ + ∂ ∂ 1 2 2 2 2 (4)

Persamaan (1) dan (2) merupakan contoh persamaan diferensial biasa, sedangkan persamaan (3) dan (4) merupakan contoh persamaan diferensial parsial.

Persamaan diferensial dibedakan menurut tingkat (orde) dan menurut derajatnya. Orde persamaan diferensial adalah tingkat derivatif tertinggi yang muncul dalam persamaan diferensial. Derajat adalah pangkat dari derivatif tingkat tertinggi yang muncul dalam persamaan diferensial. Persamaan (1) merupakan persamaan diferensial biasa orde satu dan berderajat satu, sedangkan persamaan (2) merupakan persamaan diferensial biasa orde dua dan berderajat satu. Persamaan (3) merupakan persamaan diferensial parsial orde satu dan berderajat satu, sedangkan persamaan (4) merupakan persamaan diferensial parsial orde dua dan berderajat satu.

Persamaan diferensial biasa masih bisa dibagi lagi menjadi 2 kelompok besar, yaitu persamaan diferensial linear dan persamaan diferensial non linear. Persamaan diferensial biasa tingkat n disebut linear dalam y jika persamaan diferensial dapat ditulis dalam bentuk :

) ( ) ( ) ( ) ( ) ( 1 0 1 1 ) ( x f y x a y x a y x a y x a n n n n + + + ′+ = − − L (5)

di mana a0,a1,L,an dan f adalah fungsi-fungsi kontinu pada suatu interval x dan 0

) (x ≠

a_n pada interval itu. Fungsi a_n(x) disebut fungsi-fungsi koefisien. Jadi, persamaan diferensial biasa dikatakan linear jika syarat-syarat berikut dipenuhi : 1. Fungsi yang belum diketahui dan derivatif-derivatifnya secara aljabar yang

terjadi hanya berpangkat satu.

2. Tidak ada hasil kali yang berkaitan dengan fungsi yang belum diketahui dan derivatif-derivatifnya atau dua atau lebih derivatif.

3. Tidak ada fungsi transendental dari y,y′,y′′, dan seterusnya.

Persamaan diferensial yang tidak linear disebut persamaan diferensial non linear. Jika pada persamaan (5) f(x)=0, maka persamaan itu disebut persamaan diferensial linear homogen. Tetapi jika f(x)≠ 0, maka persamaan itu disebut persamaan diferensial linear non homogen. Jika koefisien a0(x),a1(x),L,an(x) adalah konstan, maka persamaan (5) disebut persamaan diferensial linear dengan koefisien konstan, sedangkan jika koefisien-koefisiennya berupa variabel maka persamaan (5) disebut persamaan diferensial linear dengan koefisien variabel.

Persamaan diferensial linear orde dua dengan koefisien konstan mempunyai penerapan pada getaran pegas. Untuk lebih memahami penerapan persamaan diferensial linear orde dua dengan koefisien konstan pada getaran pegas, perhatikan contoh berikut.

Contoh : Sebuah benda bermassa m tergantung dari keadaan seimbang pada sebuah pegas dengan konstanta pegas k kemudian benda itu ditarik ke

bawah sejauh jarak tertentu dengan pengandaian tak ada gesekan seperti gambar di bawah ini :

Jika x menyatakan perpindahan benda dari keadaan seimbang dan F menyatakan gaya pengembalian pegas maka berdasarkan hukum Hooke F =−kx. Dengan menggunakan hukum Newton II, F =ma di mana m adalah massa benda, a adalah percepatan benda, dan F adalah gaya yang bekerja pada benda dengan massa m maka kita mempunyai hubungan : kx dt x d m ₂ = − 2 atau ₂ 0 2 = +kx dt x d m .

Persamaan di atas merupakan persamaan diferensial linear homogen orde dua dengan koefisien konstan. Persamaan karakteristiknya dapat

m k

ditulis dalam variabel r yaitu mr2 +k =0 yang mempunyai akar-akar ± = r m k i . Jika m k = 0

ω maka penyelesaian umumnya :

t c t c t x( )= 1cosω0 + 2sinω0 .

Persamaan tersebut menyatakan perpindahan benda pada saat t. Untuk menentukan penyelesaian khususnya kita harus mengetahui titik awal dan kecepatan awal dari benda yaitu :

0 ) 0

( x

x = , x′(0)=v0.

Penyelesaian dari masalah nilai awal di atas dapat diperoleh dengan mensubstitusikan penyelesaian umum ke dalam kondisi awal ini. x(t)=c₁cosω₀t+c₂sinω₀t disubstitusikan ke x(0)= x₀.

x(0)=c1cos0+c2sin0 x₀ =c₁.1+c₂.0 c1 =x0 t c t c t

x( )= ₁cosω₀ + ₂sinω₀ disubstitusikan ke x′(0)=v₀. x′(t)=−ω₀c₁sinω₀t+ω₀c₂cosω₀t

x′(0)=−ω0c1sin0+ω0c2cos0 v₀ =−ω₀c₁.0+ω₀c₂.1 ω₀c₂ =v₀

0 0 2 _ω v c =

Sehingga didapat penyelesaian khususnya :

t v t x t x ₀ 0 0 0 0cos sin ) ( ω ω ω + = .

Dari contoh di atas, dapat dilihat bahwa dalam menentukan penyelesaian khusus suatu persamaan diferensial kita perlu mengetahui kondisi awalnya. Persamaan diferensial beserta kondisi awal tersebut dinamakan masalah nilai awal. Metode-metode yang dapat digunakan untuk menyelesaikan masalah nilai awal dari persamaan diferensial linear orde dua dengan koefisien konstan misalnya metode reduksi, metode koefisien tak tentu, metode variasi parameter, dan lain-lain. Tetapi ada salah satu metode yang berbeda dengan metode lainnya yaitu metode transform Laplace.

Dalam menyelesaikan masalah nilai awal persamaan diferensial, biasanya yang pertama dilakukan adalah menentukan penyelesaian umumnya. Setelah memperoleh penyelesaian umum, kita menggunakan syarat-syarat awal yang diberikan untuk mencari penyelesaian khusus yang diinginkan. Melalui transform Laplace, kita dapat menyelesaikan masalah nilai awal tanpa mencari penyelesaian umumnya terlebih dahulu.

Transform Laplace didefinisikan sebagai berikut : misalkan f(t) suatu fungsi dari t yang terdefinisikan untuk t >0 maka transfom Laplace dari f(t) yang dinyatakan oleh L

{ }

f(t) , didefinisikan sebagai

L

{ }

∫

∞ − = = 0 ) ( ) ( ) (t F s e f t dt f st , untuk s>0.

Karena alasan itulah penulis tertarik untuk mengkaji lebih jauh transform Laplace secara teoritik dan penerapan transform Laplace dalam menyelesaikan masalah nilai awal persamaan diferensial linear orde dua dengan koefisien konstan khususnya pada getaran pegas.

B. Rumusan Masalah

Pokok permasalahan yang akan dibahas dalam penulisan ini adalah membahas transform Laplace dan bagaimana penerapan transform Laplace dalam menyelesaikan masalah nilai awal persamaan diferensial linear orde dua dengan koefisien konstan khususnya pada getaran pegas.

C. Batasan Masalah

Dalam skripsi ini, permasalahan yang akan dibahas dibatasi pada penggunaan transform Laplace dalam menyelesaikan masalah nilai awal persamaan diferensial linear orde dua dengan koefisien konstan. Untuk penerapan transform Laplace penulis akan membahas bagaimana transform Laplace

digunakan untuk menyelesaikan masalah nilai awal persamaan diferensial linear orde dua dengan koefisien konstan khususnya pada getaran pegas.

D. Tujuan Penulisan

Tujuan penulisan ini adalah untuk lebih memahami transform Laplace secara teoritik dan penerapan transform Laplace dalam menyelesaikan masalah nilai awal persamaan diferensial linear orde dua dengan koefisien konstan khususnya pada getaran pegas.

E. Metode Penulisan

Metode yang akan digunakan dalam membahas topik tersebut adalah metode studi pustaka.

F. Sistematika Penulisan

Penulisan ini terbagi dalam beberapa bab, yakni : BAB I Pendahuluan A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Metode Penulisan F. Sistematika Penulisan

BAB II Transform Laplace

A. Pengertian Transform Laplace B. Sifat-Sifat Transform Laplace C. Invers Transform Laplace

D. Transform Laplace dari Turunan dan Integral E. Konvolusi Dua Fungsi f(t) dan g(t)

F. Aplikasi Transform Laplace dalam Menyelesaikan Masalah Nilai Awal Persamaan Diferensial Linear Orde Dua dengan Koefisien Konstan

BAB III Penerapan Transform Laplace dalam Penyelesaian Masalah Nilai Awal Persamaan Diferensial Linear Orde Dua dengan Koefisien Konstan pada Getaran Pegas

A. Getaran Tak Teredam B. Getaran Teredam

C. Getaran Terpaksa Tak Teredam D. Getaran Terpaksa Teredam BAB IV PENUTUP

10

BAB II

TRANSFORM LAPLACE

A. Pengertian Transform Laplace

Definisi (transform Laplace) : Misalkan f(t) suatu fungsi dari t yang terdefinisikan untuk t >0 maka transfom Laplace dari f(t) yang dinyatakan oleh L

{ }

f(t) , didefinisikan sebagai L

{ }

∫

∞ − = = 0 ) ( ) ( ) (t F s e f t dt f st , untuk s>0.

Integral pada definisi transform Laplace merupakan bentuk integral tak wajar sehingga untuk mengerjakan integral tak wajar ini kita kerjakan :

∫

∫

− ∞ → ∞ − ₌ T st T st dt t f e dt t f e 0 0 ) ( lim ) ( .

Jadi, transform Laplace bergantung pada ada tidaknya nilai limit.

Dengan menggunakan definisi di atas, kita dapat mencari transform Laplace dari beberapa fungsi elementer.

Contoh 1: Tentukan transform Laplace dari f(t)=1, t>0. Dengan menggunakan definisi transform Laplace maka

L

{ }

1 =

∫

∞ − 0 ) 1 ( dt e st =

∫

− ∞ → T st T e dt 0 ) 1 ( lim

= T st T _s e 0 lim _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ∞ → = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − − ∞ → _{s s} e sT T 1 lim = s 1 Jadi, L

{ }

1 = s 1 , di mana s >0.

Contoh 2 : Tentukan transform Laplace dari f(t)=t, t>0. Dengan menggunakan definisi transform Laplace maka

L

{ }

t =

∫

∞ − 0 tdt e st =

∫

− ∞ → T st T e tdt 0 lim

Kita gunakan pengintegralan parsial.

Misalkan : u =t dv=e−stdt du=dt e st s v=−1 − sehingga L

{ }

t = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + ⎥⎦ ⎤ ⎢⎣ ⎡− −

_∫

− ∞ → T st T st T _ste _s e dt 0 0 1 1 lim = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− − − ∞ → T st T st T _ste _s e 0 2 0 1 1 lim

= ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ − ⎥⎦ ⎤ ⎢⎣ ⎡₋ − ₊ − ∞ → 2 2 1 1 0 1 lim s e s Te s sT sT T = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ − ⎥⎦ ⎤ ⎢⎣ ⎡− − − ∞ → 2 2 1 1 1 lim s e s Te s sT sT T = _⎢⎣⎡− − − − + _⎥⎦⎤ ∞ → 2 2 1 1 1 lim s e s Te s sT sT T = 2 1 s Jadi, L

{ }

t = 1₂ s , di mana s>0.

Contoh 3: Tentukan transform Laplace dari n t t

f( )= , t >0.

Dengan menggunakan definisi transform Laplace maka L

{ }

n t =

∫

∞ − 0 dt t e st n =

∫

− ∞ → T n st T e t dt 0 lim

Kita gunakan pengintegralan parsial.

Misalkan : u =tn dv=e−stdt du=ntn−1dt st e s v=−1 − Sehingga

∫

− ∞ → T n st T e t dt 0 lim = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + ⎥⎦ ⎤ ⎢⎣ ⎡− −

_∫

− − ∞ → T n st T st n T _s e t dt n e t s ₀ 1 0 1 lim

=

∫

− − ∞ → − ∞ → ⎥⎦ + ⎤ ⎢⎣ ⎡− T n st T T st n T _s e t dt n e t s ₀ 1 0 lim 1 lim =

∫

− − ∞ → − ∞ → ⎥⎦+ ⎤ ⎢⎣ ⎡_{− +} T n st T sT n T _s e t dt n e T s ₀ 1 lim 0 1 lim =

∫

− − ∞ → + T n st T _s e t dt n 0 1 lim 0 =

∫

− − ∞ → T n st T e t dt s n 0 1 lim L

{ }

n t = s n dt t e s n T st n T

∫

= − − ∞ → 0 1 lim L

{ }

tn−1 Apabila n diganti dengan n−1 maka L

{ }

n−1 t = s n−1 L

{ }

n−2 t sehingga L

{ }

tn = s n s n_⋅ −1 L

{ }

n−2 t = ( ₂ 1) s n n − L

{ }

n−2 t Jika diteruskan akan didapat L

{ }

n t = _n s n n n( −1)( −2)_L3⋅2⋅1 L

{ }

0 t di mana n(n−1)(n−2)_L3⋅2⋅1=n! dan L

{ }

t0 = L

{ }

s 1 1 = Jadi, L

{ }

tn = ! 1⎟= !₊₁ ⎠ ⎞ ⎜ ⎝ ⎛ n n s n s s n , di mana s >0.

Contoh 4: Tentukan transform Laplace dari f(t)=eat, t>0. Dengan menggunakan definisi transform Laplace maka

L

{ }

at e =

∫

∞ − 0 dt e e st at =

∫

∞ − − 0 ) ( dt e s at =

∫

− − ∞ → T t a s T e dt 0 ) ( lim = T t a s T _{s a} e 0 ) ( lim _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ∞ → = _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − − − − ∞ → _{s a s a} e s aT T 1 lim ) ( = a s− 1 Jadi, L

{ }

eat = a s− 1 , di mana s>a.

Contoh 5: Tentukan transform Laplace dari f(t)=sinkt, t>0. Dengan menggunakan definisi transform Laplace maka

L

{

sinkt

}

=

∫

∞ − 0 sinkt e st dt =

∫

− ∞ → T st T e kt 0 sin lim dt

Untuk mencari

∫

− T st kt e 0

sin dt kita gunakan pengintegralan parsial.

Misalkan : u =e−st dv=sinktdt dt se du=− −st kt k v=−1cos sehingga

∫

− T st kt e 0 sin dt = − −

∫

− ⎥⎦ ⎤ ⎢⎣ ⎡− T st T st kt e k s kt e k cos _{0 0} cos 1 dt Untuk mencari

∫

− T st kt e 0

cos dt kita gunakan pengintegralan parsial.

Misalkan : u =e−st dv=cosktdt dt se du=− −st kt k v= 1sin didapat

∫

− T st kt e 0 sin dt = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− − −

_∫

− T st T st T st ktdt e k s kt e k k s kt e k 0 0 ₀ sin sin 1 cos 1 = − − −

∫

− ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− T st T st T st kt e k s kt e k k s kt e k 2 ₀ 2 0 0 sin sin 1 cos 1 dt

Tambahkan kedua ruas dengan

∫

− T st kt e k s 0 2 2

sin dt akan diperoleh

∫

− ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + T st kt e k s 0 2 2 sin 1 dt = T st T st kt e k k s kt e k 0 0 sin 1 cos 1 ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− − −

∫

− ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + T st kt e k s k 0 2 2 2 sin dt = T st T st kt e k k s kt e k ₀ sin ₀ 1 cos 1 ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− − −

∫

− T st kt e 0 sin dt = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− + − − T st T st kt e k k s kt e k k s k 0 0 2 2 2 sin 1 cos 1 maka L

{

sinkt

}

= ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− + − − ∞ → T st T st T _{k k}e kt s kt e k k s k 0 0 2 2 2 sin 1 cos 1 lim = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡− + − − ∞ → T st T st T _{k k}e kt s kt e k k s k 0 0 2 2 2 sin 1 cos 1 lim = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ − ⎥⎦ ⎤ ⎢⎣ ⎡_{− +} + − − ∞ → sin 0 1 1 cos 1 lim 2 2 2 kT e k k s k kT e k k s k sT sT T = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡_{− +} + − − ∞ → _k e kT s k kT e k k s k sT sT T sin 1 cos 1 lim ₂ 2 2 2 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − ⎥⎦ ⎤ ⎢⎣ ⎡_{− +} + − ∞ → − ∞ → _k e kT s k kT e k k s k sT T sT T lim sin 1 cos 1 lim ₂ 2 2 2 = k k s k 1 2 2 2 ⋅ + = _{2 2} k s k + Jadi, L

{

sinkt

}

= _{2 2} k s k + , di mana s>0.

Contoh 6: Tentukan transform Laplace dari f(t)=coshkt, t >0. Kita ketahui bahwa

2 cosh kt kt e e kt − + = untuk k >0. Dengan menggunakan definisi transform Laplace maka L

{

coshkt

}

=

∫

∞ − 0 coshkt e st dt =

∫

∞ − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + 0 2 dt e e e kt kt st =

∫

−

(

−

)

∞ → + T kt kt st T e e e dt 0 2 1 lim = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +

_∫

∫

− − − ∞ → T kt st T kt st T e e dt e e dt 0 0 lim 2 1 = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +

_∫

∫

− + ∞ → − − ∞ → T t k s T T t k s T e dt e dt 0 ) ( 0 ) ( lim lim 2 1 = _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − + ∞ → − − ∞ → T t k s T T t k s T _{s k} e k s e 0 ) ( 0 ) ( lim lim 2 1 = _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − − − + ∞ → − − ∞ → _{s k s k} e k s k s e s kt T t k s T 1 lim 1 lim 2 1 ( ) ( ) = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + −k s k s 1 1 2 1 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − + + 2 2 2 1 k s k s k s

= ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − 2 2 2 2 1 k s s = _{2 2} k s s − Jadi, L

{

coshkt

}

= _{2 2} k s s − , di mana s> k .

Transform Laplace yang dihasilkan dari contoh-contoh tersebut dapat dirangkum menjadi sebuah tabel yang disebut tabel transform Laplace. Tetapi tabel ini tidak hanya berisi contoh-contoh di atas karena masih ada transform Laplace yang lain dan tidak mungkin untuk dibahas satu persatu. Jadi, transform Laplace dari beberapa fungsi elementer lainnya dapat dilihat dalam tabel transform Laplace pada lembar lampiran.

Dari contoh-contoh di atas dapat dilihat bahwa transform Laplace dari suatu fungsi selalu ada untuk s>0. Untuk hal tersebut terdapat teorema eksistensi transform Laplace. Tetapi terlebih dahulu akan dibicarakan mengenai pengertian fungsi kontinu sepotong-sepotong dan fungsi berorde eksponensial.

Definisi (fungsi kontinu sepotong-sepotong) : Sebuah fungsi f(t) disebut kontinu sepotong-sepotong pada sebuah interval terhingga

[ ]

a,b jika f(t) kontinu di setiap titik pada interval

[ ]

a,b selain di sejumlah titik tertentu di mana

) (t

Contoh 7: Sebuah fungsi f(t) didefinisikan dengan ⎩ ⎨ ⎧ = , 2 , 1 ) (t f 2 2 0 > < < t t . Fungsi )f(t kontinu pada selang (0,2) karena pada selang tersebut fungsi f(t) bernilai 1. Demikian pula pada selang (2,∞) fungsi f(t) kontinu karena fungsi

) (t

f bernilai 2. Dan pada t =2 terdapat dua limit yaitu 1 ) ( lim ) 2 ( 2 = = − ₋ → f t f t 2 ) ( lim ) 2 ( 2 = = + ₊ → f t f t

Jadi, fungsi f(t) tersebut kontinu sepotong-sepotong pada 0<t<∞.

Contoh 8 : Perlihatkan bahwa

⎪ ⎩ ⎪ ⎨ ⎧ − − = , 3 , 2 , ) ( 2 t t t t f 3 2 2 1 1 0 ≤ ≤ < ≤ < ≤ t t t kontinu

sepotong-sepotong dalam selang tertutup

[ ]

0,3 .

Fungsi )f(t kontinu dalam selang

[

0,1

)

karena pada selang itu f(t)=t2, )f(t juga kontinu dalam selang

[

1,2

)

. Demikian juga pada selang

[ ]

2,3 . Pada t =1,

1 ) ( lim ) 1 ( 1 = = − ₋ → f t f

t dan f(1+)=limt→1+ f(t)=1. Sedangkan pada t =2 terdapat dua limit, yaitu (2 ) lim ( ) 0

2 = = − ₋ → f t f t dan (2 ) lim ( ) 1 2 = = + ₊ → f t f t . Jadi, fungsi f(t) kontinu sepotong-sepotong dalam selang 0≤t≤3.

Definisi (fungsi berorde eksponensial) : Sebuah fungsi f(t) adalah fungsi berorde eksponensial jika ada bilangan real α , M, dan T sedemikian hingga

t

Me t

Contoh 9 : Sebuah fungsi f(t)=ektsinbt termasuk fungsi berorde eksponensial dengan α =k karena menurut definisi fungsi berorde eksponensial

bt bt e e t f e kt kt kt sin sin ) ( = − = − yang terbatas untuk semua t.

Contoh 10: Setiap fungsi yang terbatas adalah fungsi berorde eksponensial seperti sinbt dan cosbt dengan α =0.

Contoh 11 : Fungsi yang dinyatakan dengan rumus f(t)=et3 tidak termasuk fungsi berorde eksponensial karena e−αt f(t) =e−αtet3 =et3−αt menjadi tak berhingga jika t→∞ untuk berapapun nilai α.

Teorema (eksistensi transform Laplace) : Jika sebuah fungsi f(t) kontinu sepotong-sepotong pada selang

[

0,∞

)

dan berorde eksponensial α , maka transform Laplace ada untuk s>α .

Bukti :

∫

∞ − 0 ) (t dt f

e st dapat kita bagi dua menjadi

∫

∫

∞ − − ₊ T st T st dt t f e dt t f e ( ) ( ) 0 .

Integral pertama yaitu

∫

− T st dt t f e 0 )

( ada karena f(t) kontinu sepotong-sepotong dalam interval

[ ]

0,T . Untuk membuktikan bahwa integral kedua juga konvergen maka kita gunakan teorema uji banding untuk integral tak wajar yaitu jika g dan

dan andaikan

∫

∞

a

dt t

G( ) ada dan g terintegralkan dalam setiap interval a≤t<∞

maka

∫

∞

a

dt t

g( ) juga ada. Karena f(t) adalah fungsi berorde eksponensial α untuk t≥T maka berlaku

M t f

e−αt ( ) ≤ , untuk t ≥T

Kalikan dengan e−steαt sehingga kita memperoleh t st st e Me t f e− ( ) ≤ − α Andaikan g(t)= e−st f(t) dan G(t)=Me−steαt =Me−(s−α)t. Oleh karena itu,

∫

∞ − − T t s dt Me ( α) =

∫

∞ − − T t s dt e M ( α) =

∫

− − ∞ → x T t s x e dt M ( ) lim α = x T t s x _s e M _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ∞ → α α) ( lim = _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − − − − − − ∞ → α α α α s e s e M T s x s x ) ( ) ( lim = α α − − − s e M T s ) (

Jadi,

∫

∞ − − T t s dt

Me ( α) ada untuk s>α. Karena e−st f(t) ≤Me−(s−α)t untuk t≥T

dan

∫

∞ − − T t s dt

Me ( α) ada maka berdasarkan teorema uji banding, integral

∫

∞ − T st dt t f

e ( ) ada untuk s>α sehingga

∫

∞ − T st dt t f

e ( ) juga ada untuk s>α . Jadi, karena kedua integral tersebut ada maka transform Laplace F(s) ada untuk

α

> s .

B. Sifat-Sifat Transform Laplace

Selain menggunakan definisi transform Laplace untuk mencari transform Laplace, kita juga memerlukan sifat-sifat dari transform Laplace yang dapat mempermudah kita untuk mencari transform Laplace tersebut. Sifat-sifat dari transform Laplace ini dapat juga diperoleh dengan menggunakan definisi transform Laplace.

Teorema (sifat linearitas): Misalkan f₁(t) dan f₂(t) adalah fungsi-fungsi dengan transform Laplacenya masing-masing F₁(s) dan F₂(s) sedangkan c₁ dan

2

c adalah sebarang konstanta maka

L

{

c1f1(t)±c2f2(t)

}

= c1L

{

f1(t)

}

± c2L

{

f2(t)

}

= c1F1(s)±c2F2(s). Bukti :L

{

c₁f₁(t)±c₂f₂(t)

}

=

∫

∞ − _± 0 2 2 1 1 ( ) ( )) (c f t c f t dt e st

=

∫

∫

∞ − ∞ − _± 0 2 2 0 1 1 e f (t)dt c e f (t)dt c st st = c₁L

{

f₁(t)

}

± c₂L

{

f₂(t)

}

= c₁F₁(s)±c₂F₂(s)

Contoh 12 : Tentukan transform Laplace dari fungsi f(t)=sinhkt dengan menggunakan sifat linearitas.

Kita ketahui bahwa

2 sinh kt kt e e kt − − = untuk k >0 dan L

{ }

k s ekt − = 1 maka L

{

sinhkt

}

= L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − 2 kt kt e e = 2 1 L

{ }

kt − e 2 1 L

{ }

kt e− = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −k s k s 1 2 1 1 2 1 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − + 2 2 ) ( ) ( 2 1 k s k s k s = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − 2 2 2 2 1 k s k = _{2 2} k s k − Jadi, L

{

sinhkt

}

= _{2 2} k s k − , untuk s > k .

Contoh 13 : Tentukan L

{

3t+5e−2t

}

dengan menggunakan sifat linearitas. L

{

t

}

e

t 5 2

3 + − = 3L

{ }

t +5L

{ }

e−2t

Dari tabel transform Laplace diketahui bahwa L

{}

t = 1₂ s dan L

{ }

t e−2 = 2 1 + s sehingga L

{

t

}

e t 5 2 3 + − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 2 1 5 1 3 ₂ s s = ) 2 ( 5 ) 2 ( 3 2 2 + + + s s s s = ) 2 ( 6 3 5 2 2 + + + s s s s Jadi, L

{

3t+5e−2t

}

= ) 2 ( 6 3 5 2 2 + + + s s s s .

Contoh 14 : Tentukan L

{

4−3et +sint

}

dengan menggunakan sifat linearitas.

L

{

4−3et +sint

}

= 4 L

{ }

1 −3 L

{ }

et + L

{ }

sint

Dari tabel transform Laplace diketahui bahwa L

{}

1 = s 1 , L

{ }

et = 1 1 − s , dan L

{ }

sint = 1 1 2 + s sehingga

L

{

4−3et +sint

}

= 1 1 1 1 3 1 4 ₂ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ s s s = ) 1 )( 1 ( ) 1 ( ) 1 ( 3 ) 1 )( 1 ( 4 2 2 2 + − − + + − + − s s s s s s s s s = ) 1 )( 1 ( 3 3 4 4 4 4 2 2 3 2 3 + − − + − − − + − s s s s s s s s s s = ) 1 )( 1 ( 4 3 2 2 3 + − − − s s s s s Jadi, L

{

4−3et +sint

}

= ) 1 )( 1 ( 4 3 2 2 3 + − − − s s s s s .

Teorema (sifat translasi) : Jika f(t) adalah sebuah fungsi sedemikian hingga L

{ }

f(t) =F(s) ada untuk s>α maka untuk setiap konstanta a berlaku :

L

{

eat f(t)

}

=F(s−a), untuk s>α +a. Bukti :L

{ }

( ) ( ) ( ) 0 s F dt t f e t f =

∫

st = ∞ − L

{

eat f(t)

}

=

∫

∞ − 0 ) (t dt f e e st at =

∫

∞ − − 0 ) ( ) (t dt f e s at = F(s−a)

Dari tabel transform Laplace diketahui bahwa L

{

sin

}

_{2 2} k s k kt + = , s>0

Menurut sifat translasi diperoleh L

{

eatsinkt

}

= _{2 2} ) (s a k k + − Jadi, L

{

eatsinkt

}

= _{2 2} ) (s a k k + − , di mana s>a.

Contoh 16 : Dengan menggunakan sifat translasi tentukan L

{ }

eattn . Dari tabel transform Laplace diketahui bahwa L

{ }

n = _n+!₁

s n

t , s>0.

Menurut sifat translasi diperoleh L

{ }

at n t e = ₁ ) ( ! + − n a s n Jadi, L

{ }

eattn = ₁ ) ( ! + − n a s n , di mana s>a.

Contoh 17 : Dengan menggunakan sifat translasi tentukan L

{

e3tsint

}

. Dari contoh 15 telah kita ketahui bahwa L

{

eat sinkt

}

= _{2 2}

) (s a k k + − , s >a sehingga L

{

e3tsint

}

= 1 ) 3 ( 1 2 + − s .

Definisi : Jika diketahui suatu fungsi f(t) sedemikian hingga L

{ }

f(t) =F(s) maka f(t) disebut invers transform Laplace dari F(s) dan secara simbolis ditulis f(t)= L−1

{

F(s)

}

.

Invers transform Laplace juga memiliki sifat yang sama dengan transform Laplace yaitu :

1. Sifat linearitas

L−1

{

c₁F₁(s)±c₂F₂(s)

}

=c₁f₁(t)±c₂f₂(t) 2. Sifat translasi

L−1

{

F(s−a)

}

=eat f(t)

Untuk mencari invers transform Laplace, kita dapat melihat tabel transform Laplace. Kadang dalam menemukan invers transform Laplace, kita perlu mengubah bentuk persamaan fungsi F(s) agar mempunyai bentuk yang sesuai dengan tabel. Contoh 18 : Tentukan L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 9 3 2 1 s s .

Dengan menggunakan sifat linearitas dan tabel transform Laplace diperoleh L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 9 3 2 1 s s = 3 L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 9 2 1 s s = 3 L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 2 2 1 3 s s = 3cos3t

Jadi, L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 9 3 2 1 s s = 3cos3t. Contoh 19 : Tentukan L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − − 13 6 1 2 1 s s .

Kita perlu mengubah bentuk penyebut pecahan menjadi bentuk kuadrat sempurna.

2 2 2 2 2 2 ) 3 ( 1 4 ) 3 ( 1 13 9 ) 3 ( 1 13 6 1 + − = + − = + − − = + − s s s s s

Dengan menggunakan sifat translasi dan tabel transform Laplace diperoleh L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − − 13 6 1 2 1 s s = L _⎭⎬ ⎫ ⎩ ⎨ ⎧ + − − 2 2 1 2 ) 3 ( 1 s = 2 1 L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − − 2 2 1 2 ) 3 ( 2 s = e tsin2t 2 1 3 Jadi, L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − − 13 6 1 2 1 s s = e t t 2 sin 2 1 3 . Contoh 20 : Tentukan L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 3 2 1 ) 1 (s s .

Dengan menggunakan pecahan parsial diperoleh

3 2 3 2 ) 1 ( ) 1 ( 1 ) 1 ( + = + + + + s+ C s B s A s s s2 = A(s+1)2 +B(s+1)+C

s2 = As2 +2As+A+Bs+B+C s2 = As2 +(2A+B)s+(A+B+C)

Dari persamaan di atas akan kita dapatkan sistem persamaan berikut : A=1 2A+B =0 0 = + +B C A

Dari sistem persamaan di atas kita dapatkan A=1, 2B =− , dan C =1 sehingga

3 2 3 2 ) 1 ( 1 ) 1 ( 2 1 1 ) 1 (s+ = s+ − s+ + s+ s maka L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 3 2 1 ) 1 (s s = L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + + + − + − 3 2 1 ) 1 ( 1 ) 1 ( 2 1 1 s s s = L − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 1 1 1 s L _⎭⎬+ ⎫ ⎩ ⎨ ⎧ + − 2 1 ) 1 ( 2 s L _⎭⎬ ⎫ ⎩ ⎨ ⎧ + − 3 1 ) 1 ( 1 s = L − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 1 1 1 s 2 L _⎭⎬+ ⎫ ⎩ ⎨ ⎧ + − 2 1 ) 1 ( 1 s 2 1 L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 3 1 ) 1 ( 2 s = 2 2 1 2e t e t e−t − −t + −t Jadi, L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 3 2 1 ) 1 (s s = 2 2 1 2e t e t e−t − −t + −t .

Transform Laplace dari turunan dan integral sangat berguna dalam menyelesaikan masalah nilai awal persamaan diferensial linear orde dua dengan koefisien konstan.

Teorema (Transform Laplace dari turunan berorde satu) : Misalkan )

(t

f adalah fungsi yang kontinu dan merupakan fungsi berorde eksponensial α untuk t≥0 dan jika f′(t) kontinu sepotong-sepotong untuk t≥0 maka

L

{

f′(t)

}

=sL

{ }

f(t) − f(0).

Bukti : Menurut definisi transform Laplace L

{

f′(t)

}

=

∫

′ =

∫

− ′ ∞ → ∞ − T st T st dt t f e dt t f e 0 0 ) ( lim ) (

Gunakan pengintegralan parsial.

Misalkan u=e−st dv= f′(t)dt du=−se−st v= f(t) Sehingga L

{

f′(t)

}

=

[

]

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +

_∫

− − ∞ → T st T st T e f t s e f t dt 0 0 ( ) ) ( lim =

[

]

∫

− ∞ → − ∞ → + T st T T st T e f t s e f t dt 0 0 lim ( ) ) ( lim =

(

)

∫

− ∞ → − ∞ → − + T st T sT T e f T f s e f t dt 0 ) ( lim ) 0 ( ) ( lim = − f(0)+sL

{ }

f(t)

= s L

{ }

f(t) − f(0)

Teorema (transform Laplace dari turunan berorde dua) : Misalkan )

(t

f dan f′(t) adalah fungsi yang kontinu dan merupakan fungsi berorde eksponensial α untuk t≥0 dan jika f ′′(t) kontinu sepotong-sepotong untuk

0 ≥ t maka L

{

}

2 ) (t s f ′′ = L

{ }

f(t) −sf(0)− f′(0).

Bukti : Misalkan g(t)= f′(t), maka g′(t)= f ′′(t) sehingga L

{

f ′′(t)

}

= L

{

g′(t)

}

= sL

{ }

g(t) −g(0) = sL

{

f′(t)

}

− f′(0)

= s

[

sL

{ }

f(t) − f(0)

]

− f′(0) = s2L

{ }

f(t) −sf(0)− f′(0)

Contoh 21 : Tentukan L

{ }

t dengan menggunakan teorema transform Laplace dari turunan berorde satu.

Misalkan f(t)=t maka f(0)=0 dan 1f′(t)= . Menurut teorema transform Laplace dari turunan berorde satu :

L

{

f′(t)

}

= s L

{ }

f(t) − f(0) L

{ }

1 = sL

{ }

t

Dari tabel transform Laplace diketahui bahwaL

{ }

1 = s 1 sehingga s s = 1 L

{ }

t Jadi, L

{ }

t = 1₂ s .

Contoh 22 : Tentukan L

{

sinkt

}

dengan menggunakan teorema transform Laplace dari turunan berorde dua.

Misalkan f(t)=sinkt maka f′(t)=kcoskt dan f ′′(t)=−k2sinkt sehingga 0

) 0 ( =

f dan f′(0)=k. Menurut teorema transform Laplace dari turunan berorde dua :

L

{

f ′′(t)

}

= s2L

{ }

f(t) −sf(0)− f′(0) L

{

−k2sinkt

}

= s2L

{

sinkt

}

−s⋅0−k

L

{

−k2sinkt

}

= s2L

{

sinkt

}

−k

Menurut sifat linearitas 2 k − _L

{

sinkt

}

= s2L

{

sinkt

}

−k 2 s L

{

sinkt

}

+k2L

{

sinkt

}

= k ) (s2 +k2 L

{

sinkt

}

= k Jadi, L

{

sinkt

}

= _{2 2} k s k + .

Teorema (transform Laplace dari integral) : Misalkan f(t) fungsi yang kontinu sepotong-sepotong dan merupakan fungsi berorde eksponensial untuk

0 ≥ t maka L s dx x f t 1 ) ( 0 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

∫

L

{ }

f(t) = 1F(s) s untuk s>α. Bukti : Misalkan =

∫

t dx x f t g 0 ) ( )

( maka g′(t)= f(t) dan g(0)=0. Dengan menggunakan teorema transform Laplace dari turunan berorde satu diperoleh L

{

g′(t)

}

=sL

{ }

g(t) −g(0) L

{ }

f(t) = sL

{ }

g(t) L

{ }

g(t) = s 1 L

{ }

f(t) L ( ) 1 ( ) 0 s F s dx x f t = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

∫

Contoh 23 : Tentukan L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

∫

t xdx 0

dengan menggunakan teorema transform

Laplace dari integral. Misalkan =

∫

t xdx t g 0 )

( maka g′(t)= f(t)=t. Berdasarkan teorema transform Laplace dari integral diperoleh

L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

∫

t xdx 0 = s 1 L

{ }

f(t)

= s 1 L

{}

t = 1 1₂ s s⋅ = 1₃ s Contoh 24 : Tentukan L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

∫

t xdx 0

sin dengan menggunakan teorema

transform Laplace dari integral. Misalkan =

∫

t xdx t g 0 sin )

( maka g′(t)= f(t)=sint. Berdasarkan teorema transform Laplace dari integral diperoleh

L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

∫

t xdx 0 sin = s 1 L

{ }

f(t) = s 1 L

{ }

sint = 1 1 1 2 + ⋅ s s = ) 1 ( 1 2 + s s

Prosedur penting yang lain dalam hubungannya dengan penggunaan tabel transform Laplace adalah teorema konvolusi dari fungsi f(t) dan )g(t .

Definisi : Misalkan f(t) dan )g(t adalah fungsi yang kontinu sepotong-sepotong untuk t ≥0 maka konvolusi dari f(t) dan )g(t didefinisikan dengan

∫

− = ∗ t dx x g x t f t g t f 0 ) ( ) ( ) ( ) ( .

Misalkan kita ganti t−x menjadi u sehingga u=t−x maka du=−dx. Untuk 0

=

x maka u =t, sedangkan untuk x=t, u=0 sehingga

∫

− = ∗ t dx x g x t f t g t f 0 ) ( ) ( ) ( ) ( = −

∫

− 0 ) ( ) ( t du u t g u f =

∫

− t du u f u t g 0 ) ( ) ( = )g(t)∗ f(t

Jadi, konvolusi memiliki sifat komutatif yaitu f(t)∗g(t)=g(t)∗ f(t).

Contoh 25 : Tentukan konvolusi dari 1 dan sint. Misalkan f(t)=1 dan g(t)=sint

∫

⋅ = ∗ t t xdx 0 sin 1 sin 1 =

∫

t xdx 0 sin

=

[

−cosx

]

t0 = −cost+1 = 1−cost

Contoh 26 : Tentukan konvolusi dari et dan e2t. Misalkan f(t)=et dan g(t)=e2t t t e e ∗ 2 =

∫

− t x x t dx e e 0 2 ) ( =

∫

t x t dx e e 0 =

∫

t x t dx e e 0 = et

[ ]

ex t₀ = )et(et −1 = e2t −et

Contoh 27 : Tentukan konvolusi dari sint dan cos . t Misalkan f(t)=sint dan g(t)=cost

∫

− = ∗ t t t x xdx t 0 cos ) sin( cos sin

Berdasarkan rumus perkalian sinus dan cosinus :

{

sin( ) sin( )

}

2 1 cos

sehingga

[

]

∫

+ − = ∗ t dx x t t t t 0 ) 2 sin( sin 2 1 cos sin = t x t t x 0 ) 2 cos( 2 1 sin 2 1 ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ −} = _⎢⎣⎡t t+ −t − cost_⎥⎦⎤ 2 1 ) cos( 2 1 sin 2 1 = ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ −} t t t t cos 2 1 cos 2 1 sin 2 1 = tsint 2 1

Teorema (konvolusi) : Misalkan f(t) dan g(t) kontinu sepotong-sepotong dan merupakan fungsi berorde eksponensial untuk t≥0 maka transform Laplace dari f(t)∗g(t) adalah

L

{

f(t)∗g(t)

}

=F(s)G(s).

Bukti : Dengan menggunakan definisi transform Laplace dan definisi konvolusi diperoleh L

{

f(t)∗g(t)

}

=

∫

∫

∞ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − 0 0 ) ( ) (t x g x dx dt f e t st =

∫

∫

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ∞ → B t st B e f t x g x dx 0 0 ) ( ) ( lim dt

Batas dari integral berulang tersebut sesuai dengan daerah R dalam bidang tx yang diperlihatkan pada gambar 1a yaitu daerah antara sumbu t dan garis x=t. Dengan melakukan pengubahan variabel misalkan u =t−x dan v=x akan mengubah daerah R menjadi daerah R* (lihat gambar 1b) dalam bidang uv. Oleh karena itu,

L

{

f(t)∗g(t)

}

=

∫ ∫

− + − ∞ → BB v v u s B e f u g v dudv 0 0 ) ( ) ( ) ( lim =

∫ ∫

∞ ∞ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 0 0 ) (u du f e su e−svg(v)dv Jadi, L

{

f(t)∗g(t)

}

= L

{ }

f(t) L

{ }

g(t) = )F(s)G(s Gambar 1a Gambar 1b Dapat juga dikatakan

L−1

{

F(s)G(s)

}

= f(t)∗g(t)

Contoh 28 : Tentukan transform Laplace dari t e3 2∗ dengan menggunakan teorema konvolusi. Misalkan 2f(t)= dan g(t)=e3t B x 0 t R B B R* u v 0

Berdasarkan teorema konvolusi L

{

f(t)∗g(t)

}

= L

{ }

f(t) L

{ }

g(t) L

{

t

}

e3 2∗ = L

{ }

2 L

{ }

e3t = 3 1 2 − ⋅ s s = ) 3 ( 2 − s s

Contoh 29 : Tentukan transform Laplace dari t3∗sint dengan menggunakan teorema konvolusi.

Misalkan f(t)=t3 dan g(t)=sint Berdasarkan teorema konvolusi L

{

f(t)∗g(t)

}

= L

{ }

f(t) L

{ }

g(t) L

{

t3∗sint

}

= L

{ }

t3 L

{ }

sint = 1 1 ! 3 2 4 ⋅ + s s = ) 1 ( 6 2 4 + s s Contoh 30 : Tentukan L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 2 2 1 ) 1 ( 1

s dengan menggunakan teorema

konvolusi. 2 2 ) 1 ( 1 +

s dapat kita tulis menjadi 1 1 1 1 2 2 + ⋅ + s s

Dari tabel transform Laplace diketahui bahwa L t s 1 sin 1 2 1 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − sehingga L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 2 2 1 ) 1 ( 1 s = sint∗sint =

∫

− t xdx x t 0 sin ) sin(

Berdasarkan rumus perkalian sinus dan sinus :

{

cos( ) cos( )

}

2 1 sin sinα β =− α +β − α −β maka L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − 2 2 1 ) 1 ( 1 s = −

∫

[

− −

]

t x t t 0 ) 2 cos( cos 2 1 dx = t x t t x 0 ) 2 sin( 2 1 cos 2 1 ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ −} − = ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ − −} − t t t sint 2 1 ) sin( 2 1 cos 2 1 = − _⎢⎣⎡t t− t− sint_⎥⎦⎤ 2 1 sin 2 1 cos 2 1 =

[

tcost sint

]

2 1 − − = t t sint 2 1 cos 2 1 + −

F. Aplikasi Transform Laplace dalam Menyelesaikan Masalah Nilai Awal

Persamaan Diferensial Linear Orde Dua dengan Koefisien Konstan

Dalam menyelesaikan masalah nilai awal persamaan diferensial, biasanya yang pertama dilakukan adalah menentukan penyelesaian umumnya. Setelah memperoleh penyelesaian umum, kita menggunakan syarat-syarat awal yang diberikan untuk mencari penyelesaian khusus yang diinginkan. Dengan transform Laplace, kita dapat menentukan penyelesaian khusus tanpa mencari penyelesaian umumnya terlebih dahulu. Pertama-tama kita lihat bentuk umum persamaan diferensial linear orde dua dengan koefisien konstan :

) ( 0 1 2 2 2 a y f t dt dy a dt y d a + + = , di mana a2 ≠0

dengan kondisi awal y(0)=c0 dan y′(0)=c1. Kemudian kita ambil transform Laplace dari kedua ruas persamaan tersebut.

L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + + a y dt dy a dt y d a 2 1 0 2 2 = L

{ }

f(t)

Dengan menggunakan sifat linearitas transform laplace diperoleh

2 a L _{2 1} 2 a dt y d ₊ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ L a0 dt dy ₊ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ L

{ }

y(t) = L

{ }

f(t) (1)

Menurut teorema transform Laplace dari turunan dan kondisi awal yang diberikan maka L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ 2 2 dt y d = 2 s L

{ }

y(t) −sy(0)−y′(0)=s2L

{ }

y(t) −c₀s−c₁

L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ dt dy = sL

{ }

y(t) −y(0)= s L

{ }

y(t) −c0

Andaikan L

{ }

y(t) =Y(s) dan L

{ }

f(t) =F(s) maka persamaan (1) menjadi ) ( ) ( ) ) ( ( ) ) ( ( 2 _{0 1 1 0 0} 2 s Y s c s c a sY s c a Y s F s a − − + − + = (2)

Persamaan (2) merupakan persamaan aljabar dalam s. Untuk memperoleh Y(s) kita selesaikan persamaan aljabar tersebut. Kemudian kita cari invers dari transform Laplace tersebut yaitu y(t)=L−1

{ }

Y(s) dengan melihat tabel atau menggunakan metode yang sesuai (misalnya pecahan parsial, konvolusi).

Langkah-langkah di atas dapat diringkas menjadi :

1. Ambil transform Laplace dari kedua ruas persamaan diferensial.

2. Gunakan sifat linearitas, teorema transform Laplace dari turunan dan kondisi awal yang diberikan untuk memperoleh persamaan aljabar.

3. Selesaikan persamaan aljabar tersebut untuk memperoleh transform Laplacenya.

4. Cari invers transform Laplace dengan melihat tabel atau menggunakan metode yang sesuai (misalnya pecahan parsial, konvolusi) sehingga diperoleh penyelesaian masalah nilai awal yang diberikan.

Contoh 31 : Selesaikan masalah nilai awal ₂ 3 2 0 2 = + + y dt dy dt y d , 0y(0)= , 2 ) 0 ( =− ′

y dengan menggunakan transform Laplace.

L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + + y dt dy dt y d 2 3 2 2 = L

{ }

0

Langkah 2 : gunakan sifat linearitas transform Laplace.

L ₂ 3 2 + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ dt y d L +2 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ dt dy L

{ }

y(t) =L

{ }

0 (3)

Dengan menggunakan teorema transform Laplace dari turunan dan kondisi awal yang diberikan diperoleh

L ₂ 2 ( ) (0) (0) 2 ( ) 2 2 + = ′ − − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ s Y s y sy s Y s dt y d L sY(s) y(0) sY(s) dt dy _{= − =} ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

Kemudian kita substitusikan hasil yang diperoleh di atas ke persamaan (3). 0 ) ( 2 ) ( 3 2 ) ( 2 + + + = s Y s sY s Y s

Langkah 3 : menyelesaikan persamaan aljabar tersebut. 2 ) ( ) 2 3 (s2 + s+ Y s =− ) 1 )( 2 ( 2 ) 2 3 ( 2 ) ( ₂ + + − = + + − = s s s s s Y

Langkah 4 : mencari invers Y(s) yaitu L

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + + − − ) 1 )( 2 ( 2 1 s s .

Dengan menggunakan metode pecahan parsial :

1 2 ) 1 )( 2 ( 2 + + + = + + − s B s A s s