Analisa Kekokohan Tanggapan Tegangan Sistem Eksitasi Generator Terhadap Perubahan Parameterkonstanta Penguatan Generator dengan Berbagai Pengendali
Teks penuh
Gambar
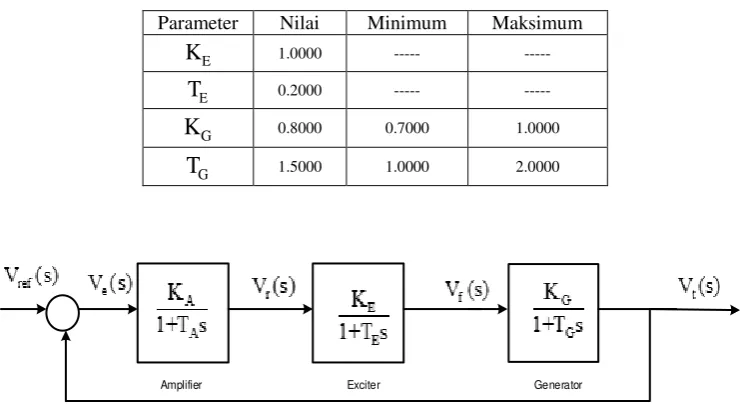
![Gambar 3.Diagram Blok Sistem Umpan Balik Multivariabel [9]. Untuk sistem yang bersifat kokoh, nilaipuncak maksimum sensitivitas kurang dari 2 (6 dB) dan nilai puncak maksimum sensitivitas komplementer kurang dari 1.25 (2 dB) [9]](https://thumb-ap.123doks.com/thumbv2/123dok/3481531.1770520/5.595.330.524.136.210/multivariabel-bersifat-nilaipuncak-maksimum-sensitivitas-maksimum-sensitivitas-komplementer.webp)
Dokumen terkait
2) Ego, merupakan bagian atau struktur kepribadian yang pertama kali dibedakan dari Id, seringkali disebut sebagai kepribadian "eksekutif' karena peranannya dalam
Berdasarkan hasil wawancara yang dilakukan di desa Karang Anyar dan desa Pinggir Papas di dapatkan hasil bahwa keuntungan (hasil yang diperoleh petani garam pada
mengembangkan sistem pusat pelayanan kegiatan ekonomi yang dapat berfungsi sebagai pusat pelayanan kegiatan sentra produksi bahan baku, kegiatan sentra
2. Faktor-faktor yang mempengaruhi tumbuh kembang balita 3. Aspek-aspek yang dinilai dalam perkembangan balita 4. Pengertian dari masing-masing aspek perkembangan balita.. Contoh
Dengan melihat kemampuan yang dimiliki oleh algoritma K-NN dalam proses klasifikasi, dan Transformasi Kosinus Diskrit dalam pengolahan sinyal untuk keperluan
Kemudian pada layar utama terdapat tombol ‘Show Original Image’ yang berfungsi untuk menampilkan kembali gambar asli image yang sudah di-load sebelumnya, Tujuan dari
Setelah tekan ENTER , maka akan tampil data tagihan pada kolom nomor 2 dan total biaya yang harus dibayar pada kolom nomor 3.. Tekan tombol BAYAR untuk melakukan proses
Dalam kompetisi itu, aktor- aktor politik (politisi dan partai politik) bertemu, bersentuhan dan membangun jejaring dengan aktor lain, seperti masyarakat sipil dan