BAB 2 LANDASAN TEORI. Interval adalah himpunan bilangan real yang berada di antara dua bilangan tertentu sebagai batas

BAB 2

LANDASAN TEORI 2.1 Interval

Interval adalah himpunan bilangan real yang berada di antara dua bilangan tertentu sebagai batas

Sifat-sifat Interval :

Jika 𝐴 = 𝑎 , 𝑎 dan 𝐵 = 𝑏 , 𝑏 dengan 0 B, maka:

- 𝐴 + 𝐵 = 𝑎 + 𝑏 , 𝑎 + 𝑏 (Penjumlahan)

- 𝐴 − 𝐵 = 𝑎 − 𝑏 , 𝑎 − 𝑏 (Pengurangan) - 𝐴 ∗ 𝐵 = min 𝑎 𝑏 , 𝑎 𝑏 , 𝑎𝑏 , 𝑎𝑏 , 𝑚𝑎𝑘𝑠{ 𝑎 𝑏 , 𝑎 𝑏 , 𝑎𝑏 , 𝑎𝑏 } (Perkalian) - 𝐴/𝐵 = 𝑎 , 𝑎 ∗ [1_𝑏,_𝑏1] (Pembagian) Jika 0∈ 𝐵, maka A / B tidak terdefinisi.

Jika A, B, dan C ∈ 𝐼( ) maka:

- 𝐴 + 𝐵 = 𝐵 + 𝐴, 𝐴 ∗ 𝐵 = 𝐵 ∗ 𝐴 (Komutatif)

- 𝐴 + 𝐵 + 𝐶 = 𝐴 + 𝐵 + 𝐶 , 𝐴 ∗ 𝐵 ∗ 𝐶 = 𝐴 ∗ (𝐵 ∗ 𝐶) (Assosiatif)

- 0,0 𝑑𝑎𝑛 1,1 , adalah elemen netral pada sifat penjumlahan dan pembagian - Interval bilangan Riil tidak memiliki pembagi 0

- Bilangan Riil 𝐴 = 𝑎, 𝑎 , 𝑎 ≠ 𝑎 tidak memiliki invers pada sifat penjumlahan dan perkalian, namun, 0 ∈ 𝐴 − 𝐴 𝑑𝑎𝑛 1 ∈ (𝐴/𝐴)\

- 𝐴 ∗ 𝐵 + 𝐶  𝐴 ∗ 𝐵 + 𝐴 ∗ 𝐶 (Subdistributif) - 𝑎 𝐵 + 𝐶 = 𝑎𝐵 + 𝑎𝐶, 𝑎 ∈ 𝑅

2.2 Linear Programming Interval Coefficient (LPIC)

Pada beberapa masalah aplikasi pemrograman linier (PL), koefisien pada model seringkali tidak bisa ditentukan secara tepat. Salah satu metode dalam menyelesaikan masalah PL ini adalah dengan menggunakan pendekatan interval, dimana koefisien tak tentu tersebut diubah menjadi bentuk interval. Bentuk PL ini dinamakan Linear Programming with Interval Coefficient (LPIC). Koefisien berbentuk interval menandakan perluasan toleransi (atau daerah) dimana parameter konstanta bisa diterima dan memenuhi model LPIC.

Salah satu metode dalam menyelesaikan LPIC yang telah dikembangkan oleh JW Chinneck dan K Ramadan (2000). Masalah LPIC memiliki fungsi objektif dan kendala persamaan atau pertidaksamaan yang berkoefisien interval. Solusi optimum dibagi menjadi dua, yaitu best optimum dan worst optimum. Dalam kasus minimisasi, best optimum adalah solusi yang memiliki nilai fungsi objektif terkecil, sedangkan worst optimum adalah solusi yang memiliki nilai fungsi objektif terbesar. Solusi optimum pada LPIC didapatkan dengan mencari versi khusus dari fungsi objektif dan kendala yang mengoptimumkan model, yaitu dipilih suatu nilai spesifik (nilai ekstrim) pada koefisien interval yang membuat model LPIC tersebut optimum, sehingga pemecahan masalah LPIC diperoleh dengan menyelesaikan PL yang mengoptimumkan model LPIC. (Farida,2011)

Bentuk linier dari persamaan LPIC adalah : Maksimum Z=



 n j 1 [𝑐_𝑗, 𝑐_𝑗]𝑥_𝑗 Kendala



 n j 1 [𝑎𝑗, 𝑎𝑗]𝑥𝑗 ≥ [𝑏𝑗, 𝑏𝑗]

Maka Best Optimum dan Worst Optimum

Best Optimum Maksimum 𝑍 =



 n j 1 𝑐𝑗𝑥𝑗 Kendala



 n j 1 𝑎_𝑗𝑥_𝑗 ≥ 𝑏_𝑗 𝑥₁ ≥ 0, … , 𝑥_𝑗 ≥ 0 Worst Optimum Maksimum 𝑍 =



 n j 1 𝑐_𝑗𝑥_𝑗 Kendala



 n j 1 𝑎_𝑗𝑥_𝑗 ≥ 𝑏_𝑗 𝑥₁ ≥ 0, … , 𝑥_𝑗 ≥ 0 (Khaled ,1996)

2.3 Program Linier Pecahan (PLP)

Bidang dari Program Linier Pecahan (PLP) secara luas dikembangkan oleh seorang matematisi Hungaria B.Martos dan asosiasinya di tahun 1960an dengan memusatkan pada masalah optimisasi. Beberapa metode penyelesaian masalah ini Charnes dan Cooper (1962) telah menyarankan metode mereka dengan bergantung pada transformasi ini (PLP) kepada ekivalen program linier. Bentuk umum dari masalah PLP dapat dibuat sbb :

Maksimumkan Z = _𝑑𝑐𝑇_𝑇𝑥+𝛼_𝑥+𝛽

Kendala 𝐴𝑥 ≤ 𝑏

0 

x

dimana 𝑥 ∈ 𝑅𝑛, x merupakan vektor dari variabel keputusan, 𝑐, 𝑑 ∈ 𝑅𝑛 dan b adalah koefisien vektor yang diketahui, 𝐴 ∈ 𝑅𝑚𝑥𝑛 adalah matriks yang diketahui dan 𝛼, 𝛽 ∈ 𝑅𝑛 adalah konstanta. Kendala permasalahan dibatasi wilayah feasible 𝑥|𝑑𝑇𝑥 + 𝛽 > 0 , yaitu wilayah yang penyebut adalah positif. Atau, penyebut dari fungsi tujuan harus negatif di daerah feasible secara keseluruhan. (Charnes & Cooper ,1962)

2.3 Program linier Optimasi.

Optimasi adalah sarana untuk mengekspresikan model matematika yang bertujuan memecahkan masalah dengan cara terbaik. Untuk tujuan bisnis, hal ini berarti memaksimalkan keuntungan dan efisiensi serta meminimalkan kerugian, biaya atau resiko. Hal ini juga berarti merancang sesuatu untuk meminimalisasi bahan baku atau memaksimalisasi keuntungan. Adapun keinginan untuk memecahkan masalah dengan model optimasi secara umum sudah digunakan pada banyak aplikasi.

Program Linier.

Program linier merupakan model umum yang dapat digunakan dalam pemecahan masalah pengalokasian sumber-sumber yang terbatas secara optimal. Masalah tersebut timbul apabila seseorang diharuskan untuk memilih atau menentukan tingkat setiap kegiatan yang akan dilakukannya, di mana masing-masing kegiatan membutuhkan sumber yang sama sedangkan jumlahnya terbatas. Secara sederhana, dapat diambil contoh bagian produksi suatu perusahaan yang dihadapkan pada masalah penentuan tingkat produksi masing-masing jenis produk dengan memperhatikan batasan faktor-faktor produksi: mesin, tenaga kerja, bahan mentah, dan sebagainya untuk memperoleh tingkat keuntungan maksimal atau biaya yang minimal.

Pada masa modern sekarang, program linier masih menjadi pilihan dalam upaya untuk memperoleh tingkat keuntungan maksimal atau biaya yang minimal. Dalam memecahkan masalah di atas, Program linier menggunakan model matematis. Sebutan “linier” berarti bahwa semua fungsi matematis yang disajikan dalam model ini haruslah fungsi-fungsi linier. Dalam Program linier dikenal dua macam fungsi, yaitu fungsi tujuan (objective function) dan fungsi-fungsi batasan (constraint function). Fungsi tujuan adalah fungsi yang menggambarkan tujuan/sasaran di dalam permasalahan program linier yang berkaitan dengan pengaturan secara optimal sumber daya-sumber daya, untuk memperoleh keuntungan maksimal atau biaya minimal. Pada umumnya nilai yang akan dioptimalkan dinyatakan sebagai Z. Fungsi batasan merupakan bentuk penyajian secara matematis batasan-batasan kapasitas yang tersedia yang akan dialokasikan secara optimal ke berbagai kegiatan.

Agar dapat menyusun dan merumuskan suatu persoalan atau permasalahan yang dihadapi ke dalam model program linier, maka ada lima syarat yang harus dipenuhi:

1. Tujuan

Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin dipecahkan dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut fungsi tujuan.

2. Alternatif perbandingan

Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan; misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu terlambat dan biaya terendah.

3. Sumber daya

Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas

4. Perumusan kuantitatif

Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif dalam apa yang disebut model matematika.

5. Keterkaitan peubah

Peubah-peubah yang membentuk fungsi tujuan dan kendala tersebut harus memiliki hubungan fungsional atau hubungan keterkaitan.

Model Dasar

Model dasar program linier dapat dirumuskan sebagai berikut:

Carilah nilai-nilai x1,x2, ,xj yang dapat menghasilkan berbagai

) . ( 2 2 1 1 tujuan fungsi x c x c x c Z     _{j j} (2.1)

Dengan syarat bahwa fungsi tujuan tersebut memenuhi kendala-kendala atau syarat-syarat ikatan sebagai berikut:

1 1 2 12 1 11x a x a x atau b a    _{j j}   2 2 2 22 1 21x a x a x atau b a     _{j j}        i j ij m i x a x a x atau b a_{1 1}  _{2 2}     (2.2)

dan bahwa: x_j  0, untuk j 1,2,..., n dan i = 1,2,…,m

(2.3)

Keterangan:



j

c Parameter yang dijadikan kriteria optimisasi, atau koefisien peubah

pengambilan keputusan dalam fungsi tujuan.



j

x Peubah pengambilan keputusan atau kegiatan (yang ingin dicari;

yang tidak diketahui).



ij

a Koefisien teknologi peubah pengambilan keputusan (kegiatan yang

bersangkutan) dalam kendala ke-i.



i

b Sumber daya yang terbatas, yang membatasi kegiatan atau usaha

yang bersangkutan; disebut pula konstanta atau “nilai sebelah kanan” dari kendala ke-i.



Asumsi – asumsi program linier 1. Linieritas

Asumsi ini menginginkan agar perbandingan antara input yang satu dengan input lainnya, atau untuk suatu input dengan output besarnya tetap dan terlepas (tidak tergantung) pada tingkat produksi.

2. Proposionalitas

Asumsi ini menyatakan bahwa jika peubah pengambilan keputusan, xj

berubah maka dampak perubahannya akan menyebar dalm proposi yang sama terhadap fungsi tujuan, cjxj, dan juga pada kendalanya, aijxj.

3. Aditivitas

Asumsi ini menyatakan bahwa nilai parameter suatu kriteria optimisasi (koefisien peubah pengambilan keputusan dalam fungsi tujuan) merupakan jumlah dari nilai individu-individu c j dalam model PL tersebut.

4. Divisibilitas

Asumsi ini menyatakan bahwa peubah-peubah pengambilan keputusan

j

X , jika diperlukan dapat dibagi ke dalam pecahan-pecahan.

5. Deterministik

Asumsi ini menghendaki agar semua parameter dalam PL (yaitu nilai – nilai cj, aij , dan bi) tetap dan dikehendaki atau ditentukan secara pasti.

Metode Simpleks

Apabila suatu masalah Linier Programming hanya mengandung dua kegiatan (variabel-variabel keputusan) saja, maka dapat diselesaikan dengan metode grafik. Bila terdapat lebih dari dua variabel maka metode grafik tidak dapat digunakan

lagi, sehingga diperlukan metode simpleks. Metode ini lazim dipakai untuk menentukan kombinasi dari tiga variabel atau lebih.

Masalah Program linier yang melibatkan banyak variabel keputusan dapat dengan cepat dipecahkan dengan bantuan komputer. Bila variabel keputusan yang dikandung tidak terlalu banyak, masalah tersebut dapat diselesaikan dengan suatu algoritma yang biasanya sering disebut metode tabel simpleks. Disebut demikian karena kombinasi variabel keputusan yang optimal dicari dengan menggunakan tabel-tabel.

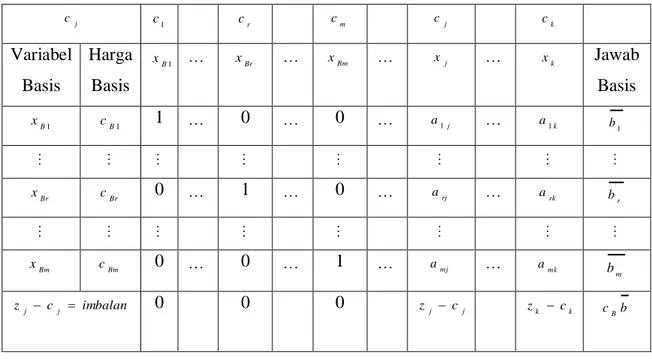
Tabel 2.1 Bentuk tabel simpleks

j c c1  ck  cn Variabel Basis Harga Basis 1 B x  x_Br x_n Jawab Basis 1 B x c_B1 a₁₁  a_1k  a_1n 1 b       Br x c_Br a_r1  a_rk  a_rn r b       Bm x c_Bm a_m1  a_mk  a_mn m b   _j j c Z imbalan Z _j  c_j  Z_k  c_k  Z_n  c_{n c b} B

Sebelum menyelesaikan suatu tabel simpleks terlebih dahulu menginisialisasikan dan merumuskan suatu persoalan keputusan kedalam model matematik persamaan linier, caranya sebagai berikut:

1. Konversikan semua ketidaksamaan menjadi persamaan.

Agar persamaan garis batasan memenuhi persyaratan penyelesaian pada daerah kelayakan (feasible) maka model program linier diubah menjadi suatu model yang sama dengan menambahkan variabel slack, surplus dan variabel buatan (artificial

variabel) pada tiap batasan (constraint) serta memberi harga nol kepada setiap koefisien C nya. Batasan dapat di modifikasi sebagai berikut:

a. Untuk batasan bernotasi   dapat dimodifikasikan kepada bentuk persamaan dengan menambahkan variabel slack ke dalam nya.

b. Untuk batasan bernotasi  atau   diselesaikan dengan menambahkan variabel surplus dan variabel buatan. Dengan penambahan variabel buatan ini akan merusak sistem batasan, hal ini dapat diatasi dengan membuat suatu bilangan besar M sebagai harga dari variabel buatan tersebut dalam fungsi tujuan. Jika persoalan maksimal maka dibuat –M sebagai harga, dan jika persoalan minimal dibuat +M sebagai harga dari variabel buatan. Cara pendekatan ini dikenal dengan metode M besar (Big M method).

Penambahan variabel slack dan variabel buatan (artificial variabel) pada tiap batasan (constrain) untuk persoalan maksimal dapat dirumuskan sebagai berikut:

Maksimalkan:





     m m i i j n j jx M B c Z 1 1 1 (2.4) Dengan batasan : 1 1 , , 2 , 1 ,i m b x x a _{j i i} n j ij    





(untuk batasan bernotasi  ) (2.5)

2 1 1 1 , , 1 ,i m m m b B x a _{j i i} n j ij     





 (untuk batasan bernotasi = ) (2.6)

m m m i b B x x a _{j i i i} n j ij , 1 2 1 , 1       





(untuk batasan bernotasi  ) (2.7)

0 

j

n j

x_j  0,  1, , ; x_i  b_i,i 1,,m ; B_i b_i,i  m₁ 1,,m

2. Menyusun persamaan – persamaan di dalam tabel awal simpleks.

Tabel 2.2 Bentuk tabel awal simpleks sebelum pivoting

j c c₁ c_r c_m c_j c_k Variabel Basis Harga Basis 1 B x  x_Br  x_Bm  x_j  x_k Jawab Basis 1 B x c_B1 1  0  0  a_1j  a_1k 1 b         Br x c_Br 0  1  0  a_rj  a_rk r b         Bm x c_Bm 0  0  1  amj  amk m b imbalan c z_j  _j  0 0 0 z_j  c_j z_k  c_k c_Bb

Langkah – langkah yang digunakan untuk menyelesaikan suatu tabel simpleks adalah sebagai berikut:

Langkah 1 : Mengecek nilai optimal imbalan.

Untuk persoalan maksimal : zk  ck = minimal {zj  cj : j R}.

Jika zk  ck  0 maka selesai, berarti jawab atau solusi sudah optimal.

Untuk persoalan minimal : zk  ck = maksimal {zj  cj : j R}.

Jika z_k  c_k  0 maka selesai, berarti jawab atau solusi sudah optimal.

j ij m j Bi j j c c a c z  



 1 (2.8)

Untuk : c_j  Harga dari semua variabel dalam z .



ij

a Koefisien dari semua variabel dalam sistem batasan.



Bi

c Harga dari variabel.

Langkah 2 : Menentukan variabel yang akan masuk dalam basis.

Untuk persoalan maksimal jika terdapat beberapa z_j  c_j  0

maka kolom yang menjadi kolom pivot adalah kolom dengan zj  cj terkecil, dan

variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk kedalam basis. Untuk persoalan minimal jika terdapat beberapa z_j  c_j  0 maka

kolom yang menjadi kolom pivot adalah kolom dengan zj  cj terbesar, dan

variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk ke dalam basis.

Langkah 3 : Menentukan variabel yang akan keluar dari basis.

Menetapkan variabel yang keluar dari basis yaitu :

imum

m i rk r a b

min

1         0 : _ik ik a a b

Variabel yang sehubungan dengan baris

pivot yang demikian adalah variabel yang keluar dari basis.

Langkah 4 : Menyusun tabel simpleks baru.

Untuk menyusun tabel simpleks yang baru, maka harus mencari koefisien elemen pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot dapat dicari dengan menghubungkan kolom pivot dengan baris pivot sedemikian rupa sehingga titik potong kedua pivot ini menunjukkan koefisien, yang disebut

elemen pivot, Koefisien – koefisien baris pivot baru dapat dicari dengan menggunakan rumus sebagai berikut :

rk rj

a a

(2.9)

Untuk menghitung nilai baris baru lainnya dilakukan dengan menggunakan rumus sebagai berikut : ik rk rj ij a a a a  (2.10)

Langkah 5 : Mengecek nilai optimal imbalan dari tabel simpleks yang baru. Jika imbalan sudah optimal maka tafsirkan hasil penyelesaian, jika belum optimal maka kembali kepada langkah 2.

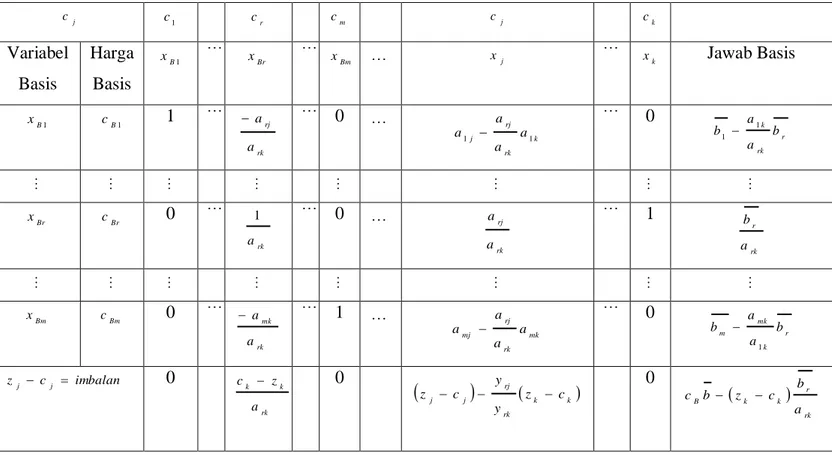
Tabel 2.3 Bentuk tabel simpleks sesudah pivoting

j c c₁ c_r c_m c _j c_k Variabel Basis Harga Basis 1 B x  x_Br  x_Bm  x_j  x_k Jawab Basis 1 B x c_B1 1  rk rj a a   0  k rk rj j a a a a₁  ₁  0 r rk k b a a b₁  1         Br x c_Br 0  rk a 1  0  rk rj a a  1 rk r a b         Bm x c_Bm 0  rk mk a a   1  mk rk rj mj a a a a   0 r k mk m b a a b 1  imbalan c z_j  _j  0 rk k k a z c  0





 _{k k} rk rj j j z c y y c z    0   rk r k k B a b c z b c  