regresi linier berganda

BAB III.

BAB III.

REGRESI LINIER BERGANDA DUA VARIABEL BEBAS

REGRESI LINIER BERGANDA DUA VARIABEL BEBAS

3.1 Pendahuluan

3.1 Pendahuluan

Dalam regresi linier sederhana telah dipelajari analisis regresi yang terdiri atas dua Dalam regresi linier sederhana telah dipelajari analisis regresi yang terdiri atas dua variabel.

variabel. Dalam pembicaraan tersebut Dalam pembicaraan tersebut di mana di mana analisisnya terdiri atas analisisnya terdiri atas sebuah variabelsebuah variabel bebas X (

bebas X (independent variableindependent variable) sering disebut variabel X atau prediktor, dan sebuah) sering disebut variabel X atau prediktor, dan sebuah variabel tak bebas Y (

variabel tak bebas Y (dependent variabledependent variable) ) atau variabel atau variabel Y Y atau atau variabel penjelaskan.variabel penjelaskan. Tentu dapat dengan mudah dimengerti bahwa, ada juga analisis regresi di mana terdapat Tentu dapat dengan mudah dimengerti bahwa, ada juga analisis regresi di mana terdapat lebih dari dua variabel, yaitu analisis regresi di mana terdapat satu variabel tergantung lebih dari dua variabel, yaitu analisis regresi di mana terdapat satu variabel tergantung (variabel Y) yang diterangkan atau dijelaskan oleh lebih dari satu variabel lain yang (variabel Y) yang diterangkan atau dijelaskan oleh lebih dari satu variabel lain yang menerangkan (variabel X) atau analisis regresi di mana terdapat lebih dari satu variabel menerangkan (variabel X) atau analisis regresi di mana terdapat lebih dari satu variabel yang tergantung (variabel Y) yang diterangkan atau dijelaskan oleh lebih dari satu yang tergantung (variabel Y) yang diterangkan atau dijelaskan oleh lebih dari satu variabel lain yang menerangkan (variabel X) yang disebut dengan analisis regresi variabel lain yang menerangkan (variabel X) yang disebut dengan analisis regresi berganda multivariat atau analisis ragam multi variat (

berganda multivariat atau analisis ragam multi variat (multivariate multiple regressionmultivariate multiple regression).).  Analisis

 Analisis regresi regresi dengan dengan satu satu variabel variabel diterangkan diterangkan atau atau variabel variabel Y oleh Y oleh lebih lebih dari dari sebuahsebuah variabel yang lain atau variabel bebas X, maka analisis yang demikian ini dinamakan variabel yang lain atau variabel bebas X, maka analisis yang demikian ini dinamakan analisis regresi majemuk atau analisis regresi berganda atau analisis regresi darab. analisis regresi majemuk atau analisis regresi berganda atau analisis regresi darab. Sangatlah jelas bahwa dalam permasalahan ini, tidak cocok lagi memakai perkataan atau Sangatlah jelas bahwa dalam permasalahan ini, tidak cocok lagi memakai perkataan atau istilah garis regresi, karena fungsi linier yang terdiri dari tiga buah variabel, sudah tidak istilah garis regresi, karena fungsi linier yang terdiri dari tiga buah variabel, sudah tidak berbentuk grafik garis lagi, melainkan berbentuk bidang atau bentuk yang lain.

berbentuk grafik garis lagi, melainkan berbentuk bidang atau bentuk yang lain.

Selanjutnya, jika variabel bebas lebih dari tiga buah, menyebabkan penggambaran Selanjutnya, jika variabel bebas lebih dari tiga buah, menyebabkan penggambaran grafiknya sangat

grafiknya sangat sulit dan sulit dan bukan berbentuk bidang bukan berbentuk bidang atau ruang. atau ruang. Bentuknya dinamakanBentuknya dinamakan multi bidang atau berbidang banyak (

multi bidang atau berbidang banyak (hyper planehyper plane).).

Grafik suatu fungsi akan berbentuk garis jika di dalam fungsi itu hanya terdapat dua Grafik suatu fungsi akan berbentuk garis jika di dalam fungsi itu hanya terdapat dua macam

macam variabel, variabel, yang yang koordinatnya koordinatnya berdemensi berdemensi dua dua atau atau bidang. bidang. Sehingga Sehingga dalamdalam penggambaran grafik dari tiga macam variabel dapat memakai istilah bidang regresi atau penggambaran grafik dari tiga macam variabel dapat memakai istilah bidang regresi atau grafiknya berdemensi

grafiknya berdemensi tiga atau tiga atau berdemensi ruang. berdemensi ruang. Tetapi istilah Tetapi istilah inipun tidak inipun tidak dapatdapat dipertahankan lagi secara bebas jika telah dipergunakan fungsi regresi yang terdiri dari dipertahankan lagi secara bebas jika telah dipergunakan fungsi regresi yang terdiri dari empat macam

empat macam atau lebih atau lebih variabel yang variabel yang dipergunakadipergunaka n. n. Sebagaimana halnya Sebagaimana halnya dalamdalam analisis regresi linier sederhana (lihat Tenaya

analisis regresi linier sederhana (lihat Tenayaet al et al ., 1985), maka di dalam analisis regresi., 1985), maka di dalam analisis regresi berganda ini juga dapat dikenal adanya:

berganda ini juga dapat dikenal adanya: 1).

1). Analisis Analisis regresi regresi linier linier berganda berganda dandan 2).

2). Analisis Analisis regresi regresi berganda berganda kurvilinier kurvilinier atau atau analisis analisis regresi regresi berganda berganda non non linier.linier. Perbedaan dari kedua analisis di atas antara analisis regresi linier berganda dengan Perbedaan dari kedua analisis di atas antara analisis regresi linier berganda dengan analisis regresi berganda kurvilinier (non linier) didasarkan atas perbedaan pada analisis regresi berganda kurvilinier (non linier) didasarkan atas perbedaan pada variabel-variabel bebas (variabel-variabel X) yang menyusunnya; atau di mana variabel-variabel Y yang berbentuk variabel bebas (variabel X) yang menyusunnya; atau di mana variabel Y yang berbentuk fungsi pangkat atau berpangkat tidak sama dengan satu.

fungsi pangkat atau berpangkat tidak sama dengan satu.

Untuk mempertegas masalah perbedaan antara analisis regresi linier berganda Untuk mempertegas masalah perbedaan antara analisis regresi linier berganda dengan analisis regresi berganda non linier, diberikan batasan dan contoh fungsinya dengan analisis regresi berganda non linier, diberikan batasan dan contoh fungsinya seperti berikut:

seperti berikut: 1).

1). Analisis regresi Analisis regresi linier berganda linier berganda didefinisikan adalah didefinisikan adalah analisis analisis regresi yregresi yang vang variabelariabel tak bebas Y ditentukan oleh sekurang-kurangnya dua variabel bebas X dan setiap tak bebas Y ditentukan oleh sekurang-kurangnya dua variabel bebas X dan setiap variabel X maupun variabel Y hanya berpangkat satu (linier).

2).

2). Analisis regresi berganda non Analisis regresi berganda non linier didefinisikan adalah sebagai analisis linier didefinisikan adalah sebagai analisis regresi diregresi di mana variabel tak bebas Y ditentukan oleh sekurang-kurangnya dua variabel bebas mana variabel tak bebas Y ditentukan oleh sekurang-kurangnya dua variabel bebas X dan yang salah satu atau kedua macam variabel mempunyai pangkat tidak sama X dan yang salah satu atau kedua macam variabel mempunyai pangkat tidak sama dengan satu.

dengan satu. Atau regresi Atau regresi di mana vdi mana variabel tak bebas ariabel tak bebas Y dengan pangkat Y dengan pangkat tidaktidak sama dengan satu ditentukan oleh sekurang-kurangnya dua variabel bebas X. sama dengan satu ditentukan oleh sekurang-kurangnya dua variabel bebas X.

3.2

3.2 Bentuk Umum

Bentuk Umum Fungsi Persamaan Regresi

Fungsi Persamaan Regresi Linier Berganda

Linier Berganda

Bentuk persamaan yang paling sederhana dari regresi linier berganda adalah yang Bentuk persamaan yang paling sederhana dari regresi linier berganda adalah yang mempunyai dua variabel bebas X dan sebuah variabel tak bebas Y seperti pada mempunyai dua variabel bebas X dan sebuah variabel tak bebas Y seperti pada persamaan berikut:

persamaan berikut: [3.1].

[3.1].  Y  Y ==





00 ++





11 X X11 ++





22 X X22

Cara lain yang umum dipergunakan pada penulisan model regresi berganda untuk dua Cara lain yang umum dipergunakan pada penulisan model regresi berganda untuk dua prediktor seperti yang dikembangkan oleh Yule dengan model persamaan di bawah ini. prediktor seperti yang dikembangkan oleh Yule dengan model persamaan di bawah ini. Persamaan regresi linier berganda model Yule seperti berikut.

Persamaan regresi linier berganda model Yule seperti berikut. [3.2].

[3.2].  Y Yii ==





 Y.12 Y.12 ++





 Y1.2 Y1.2 X Xi1i1 ++





 Y3.1 X Y3.1 Xi2i2 + e+ eii

Indeks (subscrift) dengan angka 1 pada variabel X adalah untuk variabel X

Indeks (subscrift) dengan angka 1 pada variabel X adalah untuk variabel X11 dan angka 2dan angka 2 untuk variabel X

untuk variabel X2.2. Nilai Nilai koefisien koefisien regresiregresi



Y.12

Y.12  dalam model [3.2] merupakan titik potong  dalam model [3.2] merupakan titik potong dengan sumbu tegak atau

dengan sumbu tegak atau intercept intercept , yang biasanya diartikan sebagai pengaruh rata-, yang biasanya diartikan sebagai pengaruh rata-rata (

rata (mean effect mean effect ) tehadap variabel tak bebas Y di luar variabel bebas X yang ada dalam) tehadap variabel tak bebas Y di luar variabel bebas X yang ada dalam model atau nilai rata-rata Y jika X

model atau nilai rata-rata Y jika X11 dan X dan X22  sama   sama dengan nol dengan nol (= 0). (= 0). Koefisien regresiKoefisien regresi



Y1.2

Y1.2 adalah koefisien arah atau estimator regresi Y terhadap X

adalah koefisien arah atau estimator regresi Y terhadap X11 dengan X dengan X22 dianggap konstan. dianggap konstan. Koefisien regresi

Koefisien regresi



Y3.1

Y3.1 adalah koefisien arah atau estimator regresi Y terhadap variabel X adalah koefisien arah atau estimator regresi Y terhadap variabel X22 dengan X

dengan X11 dianggap konstan.  dianggap konstan. Interprestasi dari analisis regresi Interprestasi dari analisis regresi linier berganda ini adalahlinier berganda ini adalah hampir serupa dengan interprestasi analisis regresi linier sederhana; artinya variabel hampir serupa dengan interprestasi analisis regresi linier sederhana; artinya variabel bebas X

bebas X11  bersama-sama dengan variabel bebas X  bersama-sama dengan variabel bebas X22  berpengaruh terhadap variabel tak  berpengaruh terhadap variabel tak bebas Y, yang masing-masing variabel X

bebas Y, yang masing-masing variabel Xii bekerja secara linier dan bebas sesamanya. bekerja secara linier dan bebas sesamanya.  Apabila

 Apabila antara antara variabel variabel bebas bebas XXii  tidak bersifat bebas sesamanya atau antara  tidak bersifat bebas sesamanya atau antara variabel bebas X

variabel bebas Xii, terdapat interaksi linier maka model persamaan [3.1] akan berubah, terdapat interaksi linier maka model persamaan [3.1] akan berubah bentuknya menjadi:

bentuknya menjadi: [3.3].

[3.3].  Y  Y ==



0

0 ++



1

1XX11 ++



2

2XX22 ++



12

12 XX11 X X22

Model persamaan [3.3] menunjukan adanya interaksi linier antara variabel bebas X Model persamaan [3.3] menunjukan adanya interaksi linier antara variabel bebas X11 dan variabel bebas X

dan variabel bebas X3.3. Bentuk grafik Bentuk grafik atau gambar atau gambar dari dari persamaan [3.1] atau persamaan [3.1] atau daridari persamaan [3.2] atau persamaan

persamaan [3.2] atau persamaan [3.3] berupa bidang datar [3.3] berupa bidang datar seperti Gambar 3.1 seperti Gambar 3.1 berikut.berikut. Selanjutnya, bila dari persaamaan [3.1] dimodifikasi yang terdiri atas p prediktor; di mana Selanjutnya, bila dari persaamaan [3.1] dimodifikasi yang terdiri atas p prediktor; di mana p lebih besar dari tiga (p > 3), maka model [3.1] tersebut sulit untuk digambar, karena p lebih besar dari tiga (p > 3), maka model [3.1] tersebut sulit untuk digambar, karena penggambarannya terdiri atas banyak sumbu sehingga bentuknya tidak menentu.

penggambarannya terdiri atas banyak sumbu sehingga bentuknya tidak menentu.

Berbeda halnya dengan regresi berganda non linier mempunyai bentuk gambar atau Berbeda halnya dengan regresi berganda non linier mempunyai bentuk gambar atau grafik yang berupa garis lengkung atau bidang lengkung dengan persamaan grafik yang berupa garis lengkung atau bidang lengkung dengan persamaan seperti berikut.

seperti berikut. [3.4].

[3.4].  Y  Y ==



0

0 ++



1

1 X X11 ++



11

11 X X1122 ++



2

2 X X22 ++



22

22 X X2222 ++



12

12 X X11 X X22 Bentuk grafiknya berbentuk bidang lengkung seperti pada Gambar 3.2. Bentuk grafiknya berbentuk bidang lengkung seperti pada Gambar 3.2.

2).

2). Analisis regresi berganda non Analisis regresi berganda non linier didefinisikan adalah sebagai analisis linier didefinisikan adalah sebagai analisis regresi diregresi di mana variabel tak bebas Y ditentukan oleh sekurang-kurangnya dua variabel bebas mana variabel tak bebas Y ditentukan oleh sekurang-kurangnya dua variabel bebas X dan yang salah satu atau kedua macam variabel mempunyai pangkat tidak sama X dan yang salah satu atau kedua macam variabel mempunyai pangkat tidak sama dengan satu.

dengan satu. Atau regresi Atau regresi di mana vdi mana variabel tak bebas ariabel tak bebas Y dengan pangkat Y dengan pangkat tidaktidak sama dengan satu ditentukan oleh sekurang-kurangnya dua variabel bebas X. sama dengan satu ditentukan oleh sekurang-kurangnya dua variabel bebas X.

3.2

3.2 Bentuk Umum

Bentuk Umum Fungsi Persamaan Regresi

Fungsi Persamaan Regresi Linier Berganda

Linier Berganda

Bentuk persamaan yang paling sederhana dari regresi linier berganda adalah yang Bentuk persamaan yang paling sederhana dari regresi linier berganda adalah yang mempunyai dua variabel bebas X dan sebuah variabel tak bebas Y seperti pada mempunyai dua variabel bebas X dan sebuah variabel tak bebas Y seperti pada persamaan berikut:

persamaan berikut: [3.1].

[3.1].  Y  Y ==





00 ++





11 X X11 ++





22 X X22

Cara lain yang umum dipergunakan pada penulisan model regresi berganda untuk dua Cara lain yang umum dipergunakan pada penulisan model regresi berganda untuk dua prediktor seperti yang dikembangkan oleh Yule dengan model persamaan di bawah ini. prediktor seperti yang dikembangkan oleh Yule dengan model persamaan di bawah ini. Persamaan regresi linier berganda model Yule seperti berikut.

Persamaan regresi linier berganda model Yule seperti berikut. [3.2].

[3.2].  Y Yii ==





 Y.12 Y.12 ++





 Y1.2 Y1.2 X Xi1i1 ++





 Y3.1 X Y3.1 Xi2i2 + e+ eii

Indeks (subscrift) dengan angka 1 pada variabel X adalah untuk variabel X

Indeks (subscrift) dengan angka 1 pada variabel X adalah untuk variabel X11 dan angka 2dan angka 2 untuk variabel X

untuk variabel X2.2. Nilai Nilai koefisien koefisien regresiregresi



Y.12

Y.12  dalam model [3.2] merupakan titik potong  dalam model [3.2] merupakan titik potong dengan sumbu tegak atau

dengan sumbu tegak atau intercept intercept , yang biasanya diartikan sebagai pengaruh rata-, yang biasanya diartikan sebagai pengaruh rata-rata (

rata (mean effect mean effect ) tehadap variabel tak bebas Y di luar variabel bebas X yang ada dalam) tehadap variabel tak bebas Y di luar variabel bebas X yang ada dalam model atau nilai rata-rata Y jika X

model atau nilai rata-rata Y jika X11 dan X dan X22  sama   sama dengan nol dengan nol (= 0). (= 0). Koefisien regresiKoefisien regresi



Y1.2

Y1.2 adalah koefisien arah atau estimator regresi Y terhadap X

adalah koefisien arah atau estimator regresi Y terhadap X11 dengan X dengan X22 dianggap konstan. dianggap konstan. Koefisien regresi

Koefisien regresi



Y3.1

Y3.1 adalah koefisien arah atau estimator regresi Y terhadap variabel X adalah koefisien arah atau estimator regresi Y terhadap variabel X22 dengan X

dengan X11 dianggap konstan.  dianggap konstan. Interprestasi dari analisis regresi Interprestasi dari analisis regresi linier berganda ini adalahlinier berganda ini adalah hampir serupa dengan interprestasi analisis regresi linier sederhana; artinya variabel hampir serupa dengan interprestasi analisis regresi linier sederhana; artinya variabel bebas X

bebas X11  bersama-sama dengan variabel bebas X  bersama-sama dengan variabel bebas X22  berpengaruh terhadap variabel tak  berpengaruh terhadap variabel tak bebas Y, yang masing-masing variabel X

bebas Y, yang masing-masing variabel Xii bekerja secara linier dan bebas sesamanya. bekerja secara linier dan bebas sesamanya.  Apabila

 Apabila antara antara variabel variabel bebas bebas XXii  tidak bersifat bebas sesamanya atau antara  tidak bersifat bebas sesamanya atau antara variabel bebas X

variabel bebas Xii, terdapat interaksi linier maka model persamaan [3.1] akan berubah, terdapat interaksi linier maka model persamaan [3.1] akan berubah bentuknya menjadi:

bentuknya menjadi: [3.3].

[3.3].  Y  Y ==



0

0 ++



1

1XX11 ++



2

2XX22 ++



12

12 XX11 X X22

Model persamaan [3.3] menunjukan adanya interaksi linier antara variabel bebas X Model persamaan [3.3] menunjukan adanya interaksi linier antara variabel bebas X11 dan variabel bebas X

dan variabel bebas X3.3. Bentuk grafik Bentuk grafik atau gambar atau gambar dari dari persamaan [3.1] atau persamaan [3.1] atau daridari persamaan [3.2] atau persamaan

persamaan [3.2] atau persamaan [3.3] berupa bidang datar [3.3] berupa bidang datar seperti Gambar 3.1 seperti Gambar 3.1 berikut.berikut. Selanjutnya, bila dari persaamaan [3.1] dimodifikasi yang terdiri atas p prediktor; di mana Selanjutnya, bila dari persaamaan [3.1] dimodifikasi yang terdiri atas p prediktor; di mana p lebih besar dari tiga (p > 3), maka model [3.1] tersebut sulit untuk digambar, karena p lebih besar dari tiga (p > 3), maka model [3.1] tersebut sulit untuk digambar, karena penggambarannya terdiri atas banyak sumbu sehingga bentuknya tidak menentu.

penggambarannya terdiri atas banyak sumbu sehingga bentuknya tidak menentu.

Berbeda halnya dengan regresi berganda non linier mempunyai bentuk gambar atau Berbeda halnya dengan regresi berganda non linier mempunyai bentuk gambar atau grafik yang berupa garis lengkung atau bidang lengkung dengan persamaan grafik yang berupa garis lengkung atau bidang lengkung dengan persamaan seperti berikut.

seperti berikut. [3.4].

[3.4].  Y  Y ==



0

0 ++



1

1 X X11 ++



11

11 X X1122 ++



2

2 X X22 ++



22

22 X X2222 ++



12

12 X X11 X X22 Bentuk grafiknya berbentuk bidang lengkung seperti pada Gambar 3.2. Bentuk grafiknya berbentuk bidang lengkung seperti pada Gambar 3.2.

Gambar 3.1.

Gambar 3.1. Bidang Datar Bidang Datar Regresi Regresi Dua PDua Prediktor (Regresor)rediktor (Regresor)

Y =

Y = 6.6355+6.6355+52.71452.714*x+0.192*y*x+0.192*y -106-106.989*x*x.989*x*x -0.0927-0.0927*x**x* yy -0.001*y-0.001*y *y*y

Gambar 3.2.

Gambar 3.2. Bidang Lengkung Dua Bidang Lengkung Dua Prediktor (Regresor)Prediktor (Regresor) Sebagai tambahan bahwa pada regresi non linier dapat dibedakan menjadi: Sebagai tambahan bahwa pada regresi non linier dapat dibedakan menjadi: 1).

1). Regresi non Regresi non linier sederhana, linier sederhana, adalah analisis adalah analisis regresi yregresi yang mempunyai ang mempunyai hanyahanya sebuah variabel bebas X, di mana grafiknya adalah berbentuk garis lengkung sebuah variabel bebas X, di mana grafiknya adalah berbentuk garis lengkung (bukan lurus atau linier).

(bukan lurus atau linier). 2).

2). Regresi non Regresi non linier berganda, linier berganda, adalah analisis adalah analisis regresi, yang regresi, yang mempunyai mempunyai sekurang- sekurang-kurangnya dua buah atau lebih variabel bebas X di mana grafiknya berbentuk kurangnya dua buah atau lebih variabel bebas X di mana grafiknya berbentuk bidang lengkung.

3.3 Beberapa Bentuk Fungsi Regresi Berganda Non Linier

3.3.1 Regresi fungsi polinomial

[3.5].  Y =

0

+

1 X +

2 X

2  + . . . +

p X

p

!ila pangkat tertinggi (p) sama dengan dua disebut dengan persamaan kuadratik; bila

p = 3 disebut persamaan kubik; bila p = 4 disebut persamaan kuartik; bila p = 5 disebut persamaan kuinik, dan seterusnya.

Modifikasi dari model polinomial di atas adalah:

[3.6].  Y =

0

+

1

( )

 X 1 +

2

( )

 X  2 +

2

( )

 X  3 + . . . +

p

( )

 X   p Untuk p = 2 maka modelnya menjadi:

[3.7].  Y =

0

+

1

X  +

2

( )

 X  2 atau dapat ditulis dengan

[3.8].  Y =

0

+

1 X +

2 X

½ dalam bentuk lain juga dapat seperti [3.9].  Y =

0

+

1

2 1

 

 

 



 

 

 X  +

2

2 1

 

 

 



 

 

 X  3.3.2 Regresi fungsi hiperbola (reciprocal)

[3.10].  Y = β

+

β X 

+

β  X 2

+

.. .

+

β _p X  p 2

1 0

atau dapat ditulis dengan:

[3.11].  Y2 =

0

+

1 X +

2 X

2 + . . . +

p X

p

!entuk-bentuk lain dari model di atas:

[3.12].  Y-1 =



0 +



1 X 1 +



2 X2 + . . . +



p Xp [4.13].  Y = eβ0+β1 X +β2 X 2+...+β p X  p 1

3.3.3 Regresi fungsi exponen

[3.14].  Y = e (0 +1 X1 + 2 X2) dapat pula berupa persamaan

[3.15].  Y =  X   X   X 

e

β + β + β + ...+ β 2 2 1 0

3.3.4 Regresi fungsi perkalian

[3.16].  Y =

0 X

1 X2 X3 . . . Xp

Fungsi di atas ini lebih dikenal dengan nama model fungsi Cobb-Douglas.

3.3.5 Regresi fungsi geneometri

3.3.6 Regresi fungsi gabungan [3.18].  Y =



0 X1 e2X [3.19].  Y = e  X   X   p X  p

+

+ + + + 1 1 . . . 2 2 1 0 β β β β

[3.20].  Y =

0 X1

1 e"1X1 X23. e"2X2

Selain model-model tersebut di atas, masih banyak lagi bentuk-bentuk persamaan regresi yang lainnya. Sehingga, jelas sekali bahwa penyelesaian dari bentuk-bentuk regresi di atas sangat memerlukan pengetahuan matematika yang cukup, terutama pengetahuan mengenai matriks dan operasinya.

Oleh karena itu, untuk dapat mengerjakan persamaan-persamaan tersebut di atas itu, maka sebelum pembicaraan langsung memgenai bentuk-bentuk persamaan itu, akan didahului dengan pengenalan matriks yang disajikan secara singkat.

Jadi pengenalan matriks di sini bertujuan memberikan bekal bagi yang belum pernah mendapatkan pelajaran aljabar matriks dan bagi yang sudah sekedar mengingatkan kembali operasi operasi matriks yang akan dipergunakan pada analisis regresi. Dalam analisi regresi berganda, yaitu akan dibicarakan penyelesaian persamaan regresi berganda terutama dengan metode matriks, yang sebelumnya diterangkan dengan metode simultan. Jadi disini dibicarakan bagaimana menyelesaikan olahan data yang diperoleh dari sampel, kemudian diubah menjadi bentuk matriks, sampai mendapatkan nilai parameter atau koefisien regresi (bi) yang didapat dari olahan secara simultan dan

olahan secara operasi matriks, serta uji-ujinya. Berdasarkan hal ini, peranan matriks dalam penyelesaian persamaan regresi sangat diperlukan.

3.4 Model Umum Persamaan Regresi Linier Berganda

Pada awal pembicaaan ini telah disinggung tentang macam-macam regresi berganda dengan bentuk-bentuk fungsinya. Apabila dalam persamaan regresi linier mencakup lebih dari dua prediktor atau variabel bebas X, sehingga terdapat minimal tiga variabel termasuk variabel tak bebas Y, maka regresi tersebut dinamakan regresi linier berganda (multiple linier regression).

Dalam banyak buku, penulisan persamaan regresi linier berganda mempunyai pola yang berbeda-beda, tetapi pada prinsipnya sama. Penulisan itu didasarkan pada pandangan dan tujuan dari tulisan tersebut. Seperti halnya, apakah tulisan itu ditujukan untuk menunjukkan cara pengolahan data, ataukah tulisan itu ditujukan pada pembuktian dan penurunan persamaan-persamaan ataupun mempunyai tujuan lain.

Yang jelas terdapat perbedaan penggunaan notasi yang dipakai dalam melambangkan variabel-variabel dan parameter, atau dalam pembuktian persamaan-persamaan.

Model umum regresi linier berganda seperti yang di sebutkan pada persamaam [3.2] dinyatakan kembali pada model di bawah ini.

!eberapa cara lain penulisan persamaan regresi linier berganda yang terdiri atas lebih

dari dua variabel bebas adalah:

[3.21a]. Yi =



0 +



1 X1i +



2 X2i + . . . +



p Xpi +

#

i

[3.21b]. Yi  = A +



1 X1i +



2 X2i + . . . +



p Xpi +

#

i

[3.21c]. Yi =



1 +



2 X2i +



3 X3i + . . . +



p Xpi +

#

i

[3.21d]. Yi =



0 +



1 Xi1 +



2 Xi2 + . . . +



p Xip +

#

i model untuk populasi

[3.21e]. Yi =



0 X0 +



1 Xi1 +



2 Xi2 + . . . +



p Xip +

#

i atau dapat ditulis

[3.21f]. Yi =



1.234 +



13.34 X2 +



13.24X3 + . . . +



1p.23 Xp +

#

i

[3.21g]. Yi =

$

i Xi +

#

i di mana i = 1, 2, 3, . . . .p

[3.21h]. Yi  = a + b1 X1i + b2 X2i + . . . + bp Xpi + ei

[3.21i].  Yi = b1 + b2 X2i + b3 X3i + . . . + bp Xpi + ei model untuk sampel

[3.21j].  Yi = b0 + b1 Xi1 + b2 Xi2 + . . . + bp Xip + ei

[3.21k]. Yi = b0 X0 + b1 Xi1 + b2 Xi2 + . . . + bp Xip + ei atau dapat ditulis l

[3.21l].  Yi = b1.23… + b13.34 X2 + b13.24 X3 + . . . + b1p.23 Xp + ei

[3.21m]. Yi =

$b

i Xi + ei di mana i = 1, 2, 3, . . . .p

,!, dan e adalah variabel pengganggu

Dari macam-macam model di atas, angka-angka yang tercantum pada setiap koefisien disebut indeks atau subscript. Indeks huruf i pada setiap variabel menunnjukkan pengamatan ke-i dari sampel yang diamati.

Selanjutnya, dalam uraian-uraian berikut akan menggunakan model (3.21) untuk keseragaman dalam analisis regresi.

Hubungan yang sebenarnya antara yang hendak ditaksir dan variabel bebas X pada regresi linier berganda dapat ditulis:

[3.22]. E(Yi) = B0 + B1 Xi1 + B2 Xi2 + . . . + Bp Xip

Dari model persamaan [3.22] di mana Yiadalah variabel yang dijelaskan, X1, X2 , . . ., Xp

adalah variabel-variabel bebas penjelaskan atau prediktor atau regresor. Yi  nilai

variabel Y pada pengamatan ke-i, Xi1 nilai variabel X1 pada pengamatan ke-i, dan Xip nilai

variabel Xp pada pengamatan ke-i.

Nilai-nilai B0, B1, B2, . . . , Bp adalah koefisien-koefisien regresi atau

parameter-parameter populasi yang akan ditaksir berdasarkan data sampel, dan p menunjukkan banyaknya variabel bebas X yang diduga berpengaruh terhadap variabel tak bebas Y Persamaan [3.22] dapat pula ditulis berdasarkan data sampel menjadi seperti berikut.

[3.23].  Yi = b0 + b1 Xi1 + b2 Xi2 + . . . + bp Xip + ei

Dari persamaan [3.23] yang berhubungan dengan pengamatan ke-i, yang bermaksud untuk menaksir parameter-parameter atau koefisien regresi populasi B0, B1, B2, . . . , Bp

dengan menggunakan penaksir koefisien-koefisien regresi yang berasal dari sampel atau data pengamatan yaitu: b0, b1, b2, . . . , bp. Koefisien-koefisien regresi sampel diberi

simbul bi  sebagai penaksir parameter populasi Bi. Sehingga penaksir bagi persamaan

regresi yang sebenarnya, yaitu penaksir bagi persamaan [3.22] dan [3.23] dapat ditulis sebagai berikut:

[3.24].

 %

= b0 + b1 Xi1 + b2 Xi2 + . . . + bp Xip

Persamaan [3.24] tersebut di atas yang akan dicari dengan menggunakan data berasal dari sampel. Jadi nilai

# merupakan nilai dugaan atau perkiraan terhadap nilai

 Y.

3.5 Asumsi-asumsi pada Regresi Linier Berganda

 Agar dapat menyelesaikan suatu persamaan regresi linier berganda tanpa memperhatikan sifat-sifat variabel yang dapat mempengaruhi kesimpulan hasil analisis, maka diperlukan beberapa asumsi yang berkenaan dengan analisis regresi linier berganda, sebagai berikut:

1). Rata-rata kesalahan penggangu pada setiap pengamatan sama dengan nol (0), dapat ditulis dengan: S(ei) = 0 untuk setiap nilai i. i = 1, 2, ..., n.

2). Peragam (kovarians) dari pengamatan-pengamatan sama dengan nol (0), atau

dengan istilahnya bahwa tidak ada korelasi antara kesalahan penggangu

satu dengan kesalahan pengganggu yang lainnya, dapat ditulis dengan: Kov (ei e j) = 0, untuk i

&

j.

3). Ragam (varians) kesalahan penggangu pada setiap pengamatan mempunyai

nilai yang sama, dapat ditulis dengan: Var (ei ) =

'

2

, untuk setiap nilai i. di mana i = 1, 2, ..., n.

4). Peragam (kovarians) dari pengamatan untuk setiap variabel bebas sama dengan nol (0), atau dengan lain istilahnya bahwa tidak ada korelasi antara kesalahan penggangu dari setiap variabel bebas yang satu dengan variabel bebas yang lainnya yang menysun persamaan regresi berganda tersebut, dapat ditulis dengan: Kov (ei,Xi) = 0.

5). Tidak terdapat kolinieritas ganda (multicollinierity ) yang berarti tidak terdapat hubungan linier yang kuat (eksak) antara variabel bebas X atau prediktor atau regresor yang berarti ada hubungan antara: k1 Xi1 + k2 Xi2 + . . . + kp Xip  = 0, di

mana k1 = k2 = . . . = kp  = 0, yang berarti bahwa Xi & X j adahah

terjadi kolinieritas atau linier dependen. Dalam hal ini dikatakan bahwa X1 + X2 + . . . + Xp merupakan pasangan yang terpaut linier (linier dependent )

satu sma lainnya untuk seluruh pengamatan.

Jika sebuah variabel bebas Xi  tepaut linier lebih dengan sebuah variabel bebas lain,

maka dalam analisis regresi linier berganda tersebut dikatakan terjadi kolinieritas ganda (multicollinierity ).

3.6

Regresi Linier Berganda Dua Prediktor

 Analisis regresi linier berganda yang paling sederhana dengan menggunakan hubungan linier yang terdiri atas dua buah variabel bebas X atau prediktor dengan sebuah variabel tak bebas Y atau regresor dengan bentuk fungsi atau model persamaan umum seperi pada persamaan [3.2] yang ditulis kembali pada persamaan [3.5] berikut ini.

[3.5].  Y = b0 + b1 X1 + b2 X2 (bentuk paling sederhana dari regresi linier

berganda).

Dalam regresi linier berganda seperti pada persamaan [3.2] atau [3.5] yang terdiri atas dua variabel bebas X, dapat diasosiasikan sebagai penjumlahan dari dua penyelesaian regresi linier sederhana yang secara bersamaan terhadap suatu permasalahan atau satu variabel tak bebas Y.

Dalam uraian berikut ini akan ditunjukkan penyelesaian regresi linier berganda dua variabel bebas X secara simultan untuk menentukan nilai parameter atau koefisien regresi b0; b1; dan b3. Untuk mempermudah pengertian di atas, perhatikan contoh

sederhana ini. Hasil tanaman bawang merah per hektar selain dipengaruhi oleh jumlah pupuk yang diberikan, juga dipengaruhi oleh berat atau banyaknya gulma yang tumbuh. Jika hasil bawang merah per hektar merupakan variabel tak bebas Y dan jumlah pupuk kandang yang diberikan sebagai variabel bebas X  dan berat atau banyaknya gulma

Maka dapat dikatakan bahwa Y dipengaruhi oleh X1  dan X2  secara bersama-sama.  Apabila pengertian di atas diregresikan secara linier sederhana Y dengan setiap X1 atau dengan X2 yang mempengaruhi Y masing-masing secara terpisah, maka regresi antara Y dengan X1  dan antara Y dengan X2  dapat ditulis dengan persamaan:Yi = b01 + b1 Xi1 dan Y = b02 + b2 Xi3. Selanjutnya, apabila kedua persamaan di atas dijumlahkan secara penjumlahan garis yang ortogonal atau tegak lurus satu sama lainnya, maka didapatkan nilai b01 + b02 = b0 secara bersama, sehingga kedua persamaan di atas dapat ditulis menjadi:

Yi = b01 + b1 Xi1 Yi = b02 + b2 Xi3.

[3.26].  Yi = (b01 + b02) + b1 Xi1 + b2 Xi2 atau dapat diubah menjadi:

[3.27].  Yi = b0 + b1 Xi1 + b2 Xi2 seperti persamaan [3.2] atau [3.5] dengan p = 2.

Jika dari persamaan [3.27] dipakai dasar untuk menduga koefisien regresi linier berganda bi untuk dua prediktor yaitu b0; b1; dan b2 maka modelnya dapat ditulis menjadi:

[3.28].

 %

= b0 + b1 X1 + b2 X2

3.7 Pendugaan Nilai Parameter atau Koefisien Regresi



i

Untuk menentukan nilai koefisien regresi parsial (bi)  sebagai penduga dari nilai dari



i pada persamaan [3.28], yang berasal dari data sampel, maka diperlukan sekurang-kurangnya p + 1 buah jumlah variabel pengamatan. Jika dari setiap pasangan nilai-nilai X1, X2, dan Y yang terdapat dalam setiap sampel dipandang sebagai sebuah titik, maka titik tersebut merupakan bagian dari koordinat ruang berdimensi tiga, sehingga terdapat n buah titik yang mewakili atau menggambarkan pengamatan- pengamatan yang terdapat dalam data sampel. Jika titik-titik tersebut betul-betul dilukiskan, maka gambaran yang diperoleh dengan cara demikian adalah merupakan diagram ruang bagi data sampel tersebut seperti pada Gambar 3.1. Dalam hal ini, didapatkan bentuk diagram yang sebarannya berdimensi tiga atau ruang. Gambar yang diperoleh merupakan bidang irisan dalam sebuah balok. Perhatikan Gambar 3.1.

 Analisis regresi yang akan dilakukan dalam hal yang serupa adalah bertujuan untuk menentukan bidang linier atau bidang rata atau bidang datar yang modelnya ditunjukkan seperti pada persamaan [3.28] dengan menduga nilai-nilai dari b0; b1; dan b3.

Supaya dapat dipandang sebagai bidang regresi yang baik, maka bidang irisan tersebut haruslah dihapiri sedekatnya atau didekati oleh semua titik-titik pasangan pengamatan X1i, X2i, dan Yi.

Oleh karena itu, dapatlah dikatakan bahwa titik-titik pengamatan yang ke-i atau Yi menyimpang dari bidang regresi yang merupakan pencerminan penyimpangan titik-titik pengamatan terhadap persamaan regresi linier berganda

#

= b0 + b1 X1 + b2 X2 yang akan dicari. Penyimpang tersebut disimbulkan dengane.

Penyimpangan ei  antara titik-titik pengamatan Yi  dengan bidang regresi

#

  dapat dinyatakan dengan persamaan seperti:

[3.29]. ei = Yi -

 %

  atau

[3.30]. ei = Yi - b0 - b1 X1 - b2 X2

ei = penyimpangan titik pengamatan Yi terhadap nilai pengamatan

#

Nilai ei  yang merupakan penyimpangan antara titik-titik pengamatan Yi dengan bidang regresi yang dicari atau

#

. Dengan nilai ei  ini dapat dipakai untuk menduga nilai

3.8 Metode Kuadrat Terkecil dan Persamaan Normal

 Ada dua cara untuk memperkirakan koefisien regresi parsial bi (b0; b1; dan b2)

yaitu dengan memakai methode kuadrat terkecil (Ordinary Least Squares = OLS

atau Least Squares Method   dan metode maksimum likelihood (Maximum Likelihood Method   = MLM).

Untuk selanjutnya akan diuraikan satu metode saja yaitu metode kuadrat terkecil. Dalam metode kuadrat terkecil biasa (OLS), menentukan perhitungan nilai parameter  yang tidak diketahui.

Dalam metode kuadrat terkecil (OLS) diusahakan sedemikian rupa sehingga didapatkan

 jumlah kuadrat kesalahan pengganggu atau penimpangan terhadap bidang regresi =

(

e2

haruslah mempunyai nilai sekecil-kecilnya atau minimum. Jika jumlah kuadrat kesalah

penggangu (

(

e2) dikodekan dengan G, sehingga didapatkan persamaan:

[3.31]. G =

(e

2 atau dapat ditulis menjadi:

[3.32]. G =

((Yi

- b0 - b1 X1 - b2 X2)2 dari persamaan [3.30].

Jadi, pada perhitungan nilai-nilai b0, b1, dan b2 yang dicari dengan meminimumkan nilai G pada persamaan [3.32] yang merupakan nilai-nilai penaksir atau penduga bagi

parameter-parameter



0,



1, dan



2  untuk dua pubah X1  dan X3. Cara penyelesaian

seperti ini juga berlaku bagi sejumlah p variabel bebas Xi  yang dapat diduga dengan metode matriks yang akan dibahas kemudian.

Syarat yang harus diperlukan dalam meminimali nilai G pada persamaan [3.32] adalah mengharuskan menyamakan fungsi-fungsi turunan pertama parsial dari jumlah

pangkat dua simpangan (ei) =

(

ei2 terhadap b0, b1, dan b2 yang disamakan dengan nol,

sehingga fungsi turunan

(

ei2 atau G terhadap setiap nilai b0, b1, dan b2  dapat ditulis sebagai berikut:

Turunan pertama dari

(

ei2 atau G terhadap b0 menjadi:

[3.33].

)G/)b0

= 2

((Yi

- b0 - b1 X1 - b2 X2) (- 1) = 0

Turunan pertama dari

(

e2 atau G terhadap b1 menjadi:

[3.34].

)G/)b1

= 2

((Yi

- b0 - b1 X1 - b2 X2) (- X1) = 0

Turunan pertama dari

(

e2 atau G terhadap b2 menjadi:

[3.35].

)G/)b2

= 2

((Yi

- b0 - b1 X1 - b2 X2) (- X2) = 0

Perhatikan faktor pengali yang berada di kiri tanda sama dengan nol.

 Apabila dari persamaan-persamaan di atas [3.33], [3.34], dan [3.35] diselesaikan secara serantak dan diubah cara penyajiannya, maka diperoleh persamaan-persamaan seperti:

[3.36].

(

 Yi -

(b0

- b1

(X1

- b2

(X2

= 0

[3.37].

(

 Yi X1 - b0

(X1

- b1

(X1

2 - b2

(X1X2

= 0

[3.38].

(

 Yi X2 - b0

(X2

- b1

(X1 X2

- b2

(X2

2 = 0

Persamaan-persamaan [3.36], [3.37], dan [3.38] di atas disebut dengan persamaan

normal. Perhatikan pengali dari setiap penaksir-penaksir yang berhubungan koefisien regresi seperti b0, b1, dan b3. Apabila syarat-syarat dalam meminimalkan G dipenuhi, maka sistem persamaan normal dari [3.36], [3.37], dan [3.38] dapat diselesaikan secara serentak untuk menentukan besarnya nilai-nilai b0, b1, dan b2  sebagai penaksir pangkat dua terkecil atau Least Squares Method (OLS = ordinary list squares) bagi parameter-parameter B0, B1, dan B3.

Biasanya, sistem persamaan-persamaan normal [3.36], [3.37], dan [3.38] dapat diselesaikan secara serentak untuk mendapatkan nilai- nilai b0, b1, dan b2; oleh karena  jumlah sampel (n) diketahui dan jumlah-jumlah yang terdapat dalam sistem persamaan

normal itu dapat dihitung dari data sampel. Dengan demikian koefisien-koefisien regresi b0, b1, dan b2, dalam analisis regresi linier berganda yang mengandung dua buah prediktor atau variabel bebas X dapat ditaksir atau dihitung.

3.9 Perhitungan Nilai Koefisien Regresi

Jika diperhatikan kembali sistem persaman normal dari persamaan-persamaan [3.36], [3.37], dan [3.38] dapat dilihat keteraturan dari cara-cara penyelesaianya. Sehingga setiap nilai bi dapat ditentukan dengan perhitungan seperti berikut.

Dari persamaan [3.36] dapat ditentukan nilai b0  yaitu dengan membagi persamaan tersebut dengan jumlah pengamatan (= n) sehingga didapatkan persamaan dengan penyelesaian:

(

Yi - nb0 - b1

(

X1 - b2

(

X2 = 0 sama-sama di bagi dengan n

(

Yi/n - nb0/n - b1

(

X1/n - b2

(

X2/n = 0/n atau

Y - b0 - b1 X ₁ - b2 X ₂ = 0 sehingga akhirnya menjadi [3.39]. b0 = Y  - b1  X ₁ - b2  X ₂

Dari persamaan [3.37] dan [3.38] di atas dapat ditentukan besarnya nilai b1  dan b2 dengan memodifikasi persamaannya menjadi persamaan-persamaan dengan huruf kecil. Perhatikan dengan teliti notasi dari variabel bebas X dan variabel tak bebas Y yang ditulis dengan huruf kecil x dan y pada persamaan-persamaan berikut ini.

Berikut ini diberikan hubungan antara X & Y dengan x & y:

[3.40a]. x1 = (X1 - X ₁), disebut dengan deviasi X1 [3.40b]. x2 = (X2 - X ₂),dan disebut dengan deviasi X2,dan

[3.40b]. y = (Y -Y ) disebut dengan deviasi Y

[3.41a].

(y

2 =

(

 Y2 - (( Y)2 /n disebut dengan JK Y [3.41b].

(x1

2 =

(X1

2 - ((X1)2 /n disebut dengan JK X1 [3.41c].

(x2

2 =

(X2

2 - ((X2)2 /n disebut dengan JK X2 [3.41d].

(x1y =

(X1

 Y -

(X1

(

 Y/n disebut dengan JHK X1Y [3.41e].

(x2y =

(X2

 Y -

(X2

(

 Y/n disebut dengan JHK X2Y [3.41f].

(x1x2

=

(X1X2

-

(X1

(X2

 /n disebut dengan JHK X1X2

Dengan menggunakan persamaan [3.41a] sampai dengan persamaan [3.41f] maka perhitungan nilai b1 dan b2 menjadi:

[3.42a].

(

)

2 ` 2 1 2 2 2 1 2 1 2 1 2 2 1  x  x  x  x  x  x  y  x  y  x  x b

∑

∑ ∑

∑ ∑

∑

∑

−

−

=

[3.42b].

(

)

2 2 1 2 2 2 1 2 1 1 2 2 1 2

 x

 x

 x

 x

 x

 x

 y

 x

 y

 x

 x

b

∑

∑ ∑

∑ ∑

∑

∑

−

−

=

 Atau dengan menggunakan notasi lain dari persamaan [3.41a] sampai dengan [3.41f] maka perhitungan nilai b1 dan b2 menjadi:

[3.43a].

(

)

2 2 1 2 1 2 1 2 1 2 1

 X 

 X 

 JHK 

 X 

 JK 

 X 

 JK 

 X 

 X 

 JHK 

Y 

 X 

 JHK 

Y 

 X 

 JHK 

 X 

 JK 

b

−

−

=

[3.43b].

(

)

2 2 1 2 1 2 1 1 2 1 2

 X 

 X 

 JHK 

 X 

 JK 

 X 

 JK 

 X 

 X 

 JHK 

Y 

 X 

 JHK 

Y 

 X 

 JHK 

 X 

 JK 

b

−

−

=

Selanjutnya, dilakukan pengujian terhadap regresi linier berganda terutama pengujian terhadap nilai-nilai koefisien regresi berganda (bi) serta pengujian terhadap bidang regresi atau uji varians regresi atau uji F regresi.

3.10 Pengujian Regresi Linier Berganda

Dalam pengujian regresi linier berganda terdapat tiga macam uji yaitu: 1). Uji simultan atau uji F atau uji ragam regresi atau uji varians regrsi;

2). Uji parsial koefisien regresi atau uji terhadap bi atau uji t koefisien regresi; dan 3). Uji koefisien korelasi berganda atau ujiR.

Ketiga macam uji-uji tersebut di atas menggunakan Ragam Galat Regresi atau Varians Residual Regresi yang disimbulkan dengan

*

3. Karena nilai

*

2  tidak pernah diketahui, maka nilai

*

2  didekati atau diduga dengan menggunakan nilai dugaan Galat Regresi penduga = S %2 atauSe3.

Nilai Se2  disebut dengan Kuadrat Simpangan Baku Regresi penduga atau lebih dikenal dengan sebutan Ragam Galat Regresi atau Ragam Residual Regresi atau Varians Residual Regresi atau Varians Sisa Regresi atau Varians Galat Regresi. Ragam Galat Regresi = Se2, yang perhitungannya didasarkan pada Jumlah Kuadrat Kesalahan Penggangu yang sering disebut dengan Jumlah Kuadrat Residual Regresi (JK Galat Regresi = JK Sisa Regresi = JK Residual yang disingkat dengan = JK Galat Regresi dengan simbul

(e

i2) dibagi dengan Derajat Bebas Galat Regresi = DB Galat Regresi yang besarnya sama dengan n - p - 1.

Dasar perhitungan dari KT Galat Regresi atau Varians Residual Regresi adalah menggunakan persamaan [3.30] yaitu nilai variabel pengganggue  yang ditulis kembali menjadi persamaan:

[3.44]. ei = Yi - b0 - bi Xi1 - b2 Xi2

Dan jika ke dalam persamaan [3.44] disubstitusikan persamaan [3.39] yaitu pesamaan untuk perhitungan b0 maka didapatkan persamaan:

[3.45a]. ei = Yi - (Y - b1 X ₁ - b2 X ₂) - bi Xi1 - b2 Xi2 dengan membuka kurung maka menjadi:

[3.45b]. ei = (Yi -Y ) - b1 (Xi1 -  X ₁) - b2 (Xi2 -  X ₂) [3.45c]. ei =yi - b1 x1 - b2 x3.

Dan dari persamaan [3.44] yaitu persamaan untuk nilaiei = Yi - b0 - bi Xi1 - b2 Xi2 sehingga dengan mengkuadrat jumlahkan nilai ei; selanjutnya didapatkan

)

ei

2   atau disebut dengan JK Galat Regresi dengan kode G; dengan persamaannya menjadi:

[3.46a]. G =

)

 ei 2

  atau

[3.46b]. G =

)

eiei.

Ingat ei =yi - b1 x1 - b2 x3. Seperti persamaan [3.45c] sehingga: [3.46c]. G =

$

ei(yi - b1 x1 - b2 x2) atau [3.46d]. G =

$

eiyi - b1

$

eI x1 - b2

$

eI x2)

[3.46e]. G =

$

eiyi  sebab

)eI

 x1 =

)eI

 x2 = 0. sehingga menjadi: [3.46f]. G =

$

yiei

[246g]. G =

$

yi (yi - b1

$

x1 - b2

$

x2) sehingga menjadi: [3.46h]. G =

$

yiyi - b1 yi

$

x1 - b2

$

yi x2

Ingat : yiyi =

)yi

2

= JK Total = JK Y

)yix1

= JHK YX1 = JHK X1Y Ingat persamaan [3.41a sd 3.17f].

)yix2

= JHK YX2 = JHK X2Y

b1

)

yix1 + b2

)

yix2 disebut dengan JK Regresi

Dari persamaan [3.46 h] didapatkan bahwa JK Galat Regresi atau JK Residual Regresi Linier berganda sama dengan JK Total dikurangi dengan JK Regresi. Di mana JK Total = JK Y.

Hubungan antara komponen-komponen pada analisis keragaman (JK Total, JK Regresi, dan JK Galat Regresi) seperti berikut:

[3.47]. JK Galat Regresi = JK Total - JK Regresi.

Untuk menyederhanakan penulisan dan pengertian di atas, maka selanjutnya JK Galat Regresi disingkat dengan JK Galat, JK Regresi dengn JK Reg (tanpa titik) dan JK Total dengan JK Tot atau JK Y (tanpa titik).

Sehingga sesuai dengan persamaan [3.47], maka JK Regresi dua prediktor (dua variabel bebas X) mempunyai persamaan:

[3.485a] JK Regresi = (b1

$

yi x1 + b2

$

yi x2) atau dapat ditulis: [3.48b] JK Regresi = (b1 JHK X1 Y + b2JHK X2 Y)

Persamaan [248a,b] berlaku umum untuk p  variabel bebas X sehingga persamaannya menjadi:

[249a] JK Regresi = b1

$

yi x1 + b2

$

yi x2+ . . . + bp

$

yi xp

[3.49b] JK Regresi = (b1 JHK X1 Y + b2JHK X2 Y + . . . + bp JHK Xp Y)

Setelah perhitung JK Total, JK Regresi, dan JK Galat Regresi didapat maka di lanjutkan dengan uji F atau Analisis Keragaman atau Analisis Varians Regresi seperti uraian berikut.

3.11 Uji F atau Analisis Keragaman atau Analisis Varians Regresi

Dalam analisis keragaman yang merupakan uji F terhadap Ragam Regresi (KT Regresi atau Kuadrat Tengah Regresi) dengan memakai Ragam Galat (KT Galat = KT Residu). Dalam pengujian ini didasarkan pada pemecahan JK Total menjadi komponen-komponennya yaitu JK Regresi dan JK Galat Regresi, yang selanjutnya dijadikan Ragam Regresi dan Ragam Galat Regresi. Untuk memudahkan dalam uji F ini biasanya dibuatkan tabel Analisis Keragaman (Tabel Sidik Ragam Regresi atau Tabel Analisis Varians Regresi atau ANAVA Regresi atau ANOVA Regresi) yang komponen-komponennya seperti berikut.

Komponen Penyusun Tabel Sidik Ragam Regresi adalah:

1). JK Regresi = b1 JHK X1Y + b2JHK X2Y (untuk 2 prediktor) atau

= b1 JHK X1Y + b2JHK X2Y + . . . + bp JHK XpY

(untuk p buah prediktor) 2). JK Total = Jk Y =

(

Y2 - (

(

Y)2/n

3). JK Galat = JK Total - JK Regresi

Selanjutnya dihitung nilai KT atau Varians seperti:

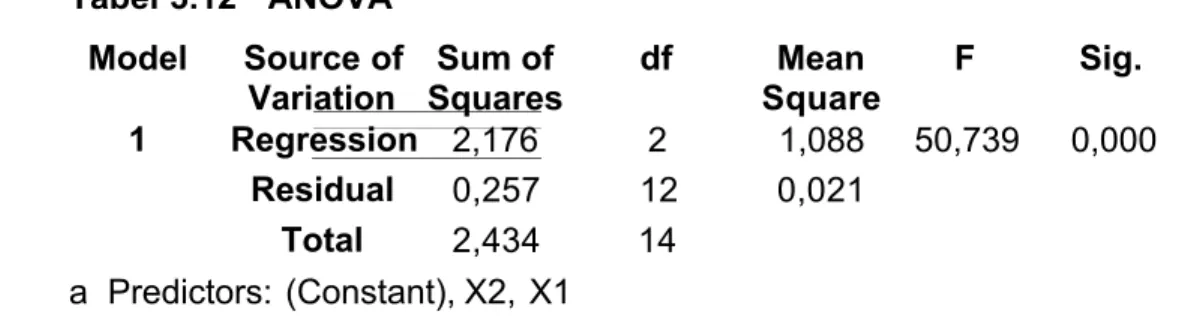
1). KT Regresi = JK Regresi/(db Regresi). (DB Regresi = p. p = jumlah variabel X) 2). KT Galat = JK Galat/(db Galat) (DB Galat = n-p-1 n = jumlah sampel) Hasil perhitungan keragaman atau analisis varians di atas dibuatkan Tabel Sidik Ragam Regresi seperti pada Tabel 3.1.

Tabel 3.1. Bagan Sidik Ragam Regresi Berganda Dua Prediktor Sumber Keragaman (JK) Derajat Bebas (DB) Jumlah Kuadrat (JK) Kuadrat Tengah (KT) F hitung F tabel 5% 1% Regresi p = 2 B1 yi x1 + b2 yi x2 atau [ (biJHK XiY)] JK Reg/p = KT Reg _KTGalat Regresi KT Lihat tabel F Residual atau Galat n - p – 1 JK Galat 1  p n Galat JK 

−

−

Total n – 1 =

(

yi = JK Tot = JK Y n = jumlah sampel.

Berdasarkan pada asumsi sebaran normal untuk komponen pengganggu e, maka besarnya nilai F (F-hitung) dapat dihitung dengan rumus adalah:

[3.50] Fhit =

Galat   KT 

 gresi  KT Re

F-hitung disimbulkan dengan Fhit  yang digunakan dalam pengujian hipotesis akan

dibuktikan dengan uji hipotesis.

Kreteria pengujian nilai Fhit  adalah:

1). Jika Fhit > F(tabel

*

) ini berarti bahwa terdapat hubungan bukan linier berganda

pada pasangan pengamatan X1,X2,Y tersebut atau f = (X1, X2) adalah bukan

linier pada taraf

*.

2). Jika Fhit

+

F(tabel

*

) ini berarti bahwa terdapat hubungan linier berganda antara

pengaruh X1 dan X2  terhadap Y secara bersama atau simultan pada taraf

*.

Pengujian yang dilakukan dengan uji F seperti cara tersebut di atas, tidak dapat memberikan petunjuk apakah setiap variabel bebas Xi  menunjukkan pengaruh

atau hubungan yang nyata terhadap variabel tak bebas Y secara parsial.

Oleh karena itu, maka untuk menunjukkan hubungan atau pengaruh masing-masing variabel bebas Xi  secara individu atau parsial dalam kebersamaan atau simultan

terhadap variabel tak bebas Y, dapat dilakukan dengan menguraikan analisis keragaman yaitu menguraikan JK Regresi menjadi JK Regresi parsial untuk setiap variabel bebas Xi

seperti uraian berikut ini.

JK Regresi berganda = b1 JHK X1Y + b2JHK X2Y + . . . + bp  JHK XpY (untuk p

prediktor) yang dapat diuraikan menjadi seperti berikut: 1). JK Regresi X1 = b1 JHK X1Y 2). JK Regresi X2 = b2 JHK X2Y . . . . . . p). JK Regresi Xp = bp JHK XpY

Untuk dua variabel bebas X, maka JK regresi parsial variabel bebas X1 dan X2 adalah:

JK Regresi = b1 JHK X1Y + b2JHK X2Y (untuk 2 prediktor) dapat diuraikan menjadi:

1). JK Regresi X1 = b1 JHK X1Y

2). JK Regresi X2 = b2 JHK X2Y

Dengan demikian maka bentuk Tabel Sidik Ragam Regresi dari uraian di atas untuk dua variabel bebas X dapat ditulis seperti pada Tabel 3.2 di bawah ini.

Tabel 3.3. Sidik Ragam Regresi Berganda Dua Prediktor Sumber Keragaman (SK) Derajat Bebas (DB) Jumlah Kuadrat (JK) Kuadrat Tengah (KT) F hitung F tabel (Fhit) 5% 1% Regresi p JK Regresi KT Regresi

Regresi X1 1 JK Regresi X1 KT Regresi X1

Regresi X2/X1 1 JK Regresi X2 KT Regresi X2

Residual atau Galat

n-p-1 JK Galat KT Galat Total n-1 JK Total

Dari Sidik Ragam Tabel 3.3 di atas terlihat bahwa JK Regresi, dapat diuraikan mendi JK Regresi komponen-komponen setiap variabel bebas Xi dengan derajat bebas tiap komponen sama dengan satu yaitu JK Regresi X1  dan JK Regesi X2/X1  artinya JK Regresi dari X2  jika X1  dianggap konstan, atau variabel X2  merupakan tambahan terhadap variabel bebas X1  dalam mempengaruhi variabel tak bebas Y; demikian selanjutnya apabila jumlah variabel bebas bertambah samapai sebanyak p buah.

3.12 Uji Keberartian Koefisien Regresi (b

i

) Secara Parsial

atau Uji t Koefisien Regresi

Pengujian yang dilakukan dengan uji F seperti cara tersebut pada Tabel 3.3 di atas, dapat memberikan petunjuk apakah setiap variabel Xi  menunjukkan pengaruh atau hubungan yang nyata terhadap variabel tak bebas Y secara parsial.

Modifikasi dari pengaruh masing-masing variabel bebas Xi  secara individu atau parsial dalam kebersamaan atau simultan terhadap variabel tak bebas Y, dapat dilakukan dengan uji t atau uji koefisien regresi secara parsial.

Secara umum uji t mempunyai persamaan seperti berikut: [3.51]. t-hitung W =

w

S  W 

W nilai yang diuji, sehingga untuk pengujian koefisien regresi (bi), maka persamaananya menjadi: [3.52]. t-hitung b1 = 1 1 b S  b ; t-hitung b2 = 2 2 b S  b ; dan seterusnya

Di mana Sbi = salah baku bi Dari persamaan [3.52] dalam menyederhanakan penulisan Salah Baku Koefisien Regresi Bi biasa ditulis dengan

'

Bi (Salah Baku = Standard Error Koefisien RegresiBi ). Perhitungannya didasarkan pada Ragam Galat Regresi atau KT Galat Regresi. Karena besarnya nilai

'

2e (Ragam Galat Regresi Populasi) tidak diketahui, maka dapat diduga dengan nilai S2e atau KT Galat Regresi penduga yang mempunyai persamaan yaitu:

[3.53]. S2e = KT Galat Regresi = JK Galat Regresi/(n-p-1) (Perhatikan Tabel 3.2)

Selanjutnya, dalam Analisis Regresi dua prediktor, nilai Salah Baku bi  yang ditulis (Sbi) mempunyai persamaan seperti:

[3.54]. Sbi = var bi masing-masing untuk b1 dan b2 menjadi:

Untuk pengujian b1nilai salah baku menjadi: [3.55a]. Sb1 = var b1 =

(

)

 

 

 

 





 

 

−

2 2 1 2 1 2 Re  X   X   JHK   X   JK   X   JK   X   JK   gresi Galat   KT 

Untuk pengujian b2nilai salah baku menjadi: [3.55b]. Sb2 = var b₂ =

(

)

 

 

 

 





 

 

−

2 2 1 2 1 1 Re  X   X   JHK   X   JK   X   JK   X   JK   gresi Galat   KT 

Seperti dalam uji F, penulisan t-hitung dapat ditulis dengan notasi thitung (artinya uji t untuk

pengujian hipotesis nol atau H0 : bi  = 0 dan H1 : minimal satu dari bi

&

  0).

Berdasarkan hasil uji t ternyata bahwa kreteria pengujian nilai thitung  adalah:

1). Jika thitung

+

t(tabel 5%, db galat) ini berarti pada analisis regresi linier berganda, pengaruh

X1 dan X2  terhadap Y menunjukkan bahwa baik X1 maupun X2

berpengaruh tidak nyata secara parsial terhadap Y.

2). Jika thitung > t(tabel 5%, db galat) maka nilai bi menunjukkan bahwa masing-masing baik X1

maupun X2 berpengaruh nyata terhadap variabel bebas Y secara

individual dalam kebersamaan atau secara parsial. Dengan kata lain ini berarti bahwa koefisien arah bi yang berangkutan dapat dipakai sebagai

penduga dan peramalan yang dapat dipercaya.

Pengujian yang dilakukan dengan cara tersebut di atas, dapat memberikan petunjuk apakah setiap variabel bebas Xi  memberikan pengaruh atau hubungan yang nyata

terhadap variabel tak bebas Y.

Perlu diingatkan di sini ialah bahwa dalam pengujian-pengujian di atas (baik uji F maupun uji t), didasarkan atas metode kuadrat terkecil (OLS).

Selanjutnya, nilai Salah Baku Koefisien Regresi atau Sbi  yang diperoleh selain untuk

pengujian hipotesis juga dapat dipakai pada perkiraan nilai interval koefisien regresi parsial yang sering disebut dengan perkiraan nilai beta (



) populasi dengan persamaan sebagai berikut di bawah ini.

[3.56]. p {bi - t! /2 Sbi <



i < bi + t! /2 Sbi} = 1-

!

untuk setiap b1 dan b1 seperti:

[3.57a]. p {b1 - t! /2 Sb1 <



1 < b1 + t! /2 Sb1} = 1-

!

untuk b1

[3.57b]. p {b2 - t! /2 Sb2 <



2 < b2 + t! /2 Sb2} = 1-

!

untuk b2

3.13 Koefisien Korelasi dan Koefisien Determinasi

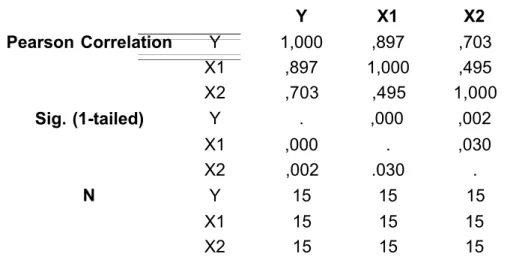
Dalam analisis regresi linier berganda terdapat beberapa macam koefisien korelasi, yang tergantung pada pendekatan hubungan yang dicari.

 Adapun macam-macam koefisien korelasi tersebut ad alah: 1). Koefisien korelasi sederhana.

2). Koefisien korelasi parsial. 3). Koefisien korelasi berganda. 4). Koefisien determinasi.

3.13.1 Korelasi linier sederhana

Koefisien korelasi sederhana atau koefisien korelasi linier atau koefisien korelasi product moment atau koefisien korelasi Pearson yang disimbulkan denganr ij;  yaitu suatu nilai

mengukur keeratan hubungan antar masing-masing variabel ke-i dengan variabel ke-j, dengan tidak memperhatikan pengaruh variabel-variabel yang lainnya, seperti variabel tak bebas Y atau sesama variabel bebas X dalam analisis regresi berganda.

Dalam analisis regresi berganda tiga variabel atau dua prediktor yaitu analisis regresi yang terdiri atas dua pubah bebas X yaitu X1 dan X2 serta sebuah variabel tak bebas Y,

maka terdapat tiga nilai koefisien korelasi linier sederhanar ij yaitu:

1) r Y1  atau r YX1 yaitu koefisien korelasi antara Y dengan X1;

2) r Y2  atau r YX2 yaitu koefisien korelasi antara Y dengan X2; dan

3) r 12  atau r X2X1 yaitu koefisien korelasi antara X1 dengan X3.

Koefisien-koefisien korelasi tersebut di atas disebut dengan koefisien korelasi linier sederhana atau koefisien korelasi tahap nol atau koefisien korelasi order nol (simple coeficient of correlation or correlation coeficients of zero order ).

 Adapun rumus dari koefisien korelasi sederh ana ini adalah:

[3.58a]. r XY =

( )

( )

 

 

 

 



 

 

∑

−

∑

 

 

 

 



 

 

∑

−

∑

∑

−

∑ ∑

n Y  Y  n  X   X  n Y   X   XY  2 2 2 2 atau [3.58b]. r XY =

∑

∑

∑

2 2  y  x  xy   atau [3.58c]. r XY =

(

 JK  X 

)( )

 JKY   XY   JHK  (n = jumlah sampel)

Memperhatikan keterangan di atas dapatkah dikatakan bahwa r YX1  merupakan ukuran

dari keeratan huhungan atau korelasi sederhana antara Y dengan X1  yang sebenarnya,

tanpa ada pengaruh yang variabel lain; sementara diketahui bahwa yang mempengaruh nilai Y adalah X2 selain nilai X1 dan selain itu kemungkinan juga X2 mempengaruhi X1 .

Jadi tegasnya bahwa dalam regresi berganda untuk mendapatkan hubungan yang sebenarnya antara sebuah variabel bebas Xi dengan variabel tak bebas Y, yaitu dengan

cara menghilangkan pengaruh variabel-variabel bebas yang lainya. Analisis ini dikenal dengan nama analisiskorelasi parsial.

3.13.2 Koefisien korelasi parsial

Korelasi parsial ( partial corelation coeficient ) dapat dibedakan menjadi: 1) korelasi parsial order satu, 2) korelasi parsial order dua, 3) korelasi parsial order tiga, dan 4) dan korelasi parsial order empat sampai korelasi parsial order banyak.

1). Korelasi parsial order satu, dengan simbulr XiXj.Xk.  yang berarti hubungan antara

variabel X ke-i dengan variabel X ke-j yang bebas dari pengaruh variabel X ke-k. 2). Korelasi parsial order dua, dengan simbulr YXi.XjXk.  yang berarti hubungan antara

variabel Y dengan variabel X ke-i yang bebas dari pengaruh variabel X ke-j dan variabel X ke-k.

3). Korelasi parsial order tiga, dengan simbul r YXi.XjXkXl.  yang berarti hubungan

antara variabel Y dengan variabel X ke-i yang bebas dari pengaruh variabel-variabel X ke-j; X ke-k; dan X ke-l.

4). Korelasi parsial order banyak, dengan simbulr YXi.XjXk . . . Xp.  yang berari hubungan

antara variabel Y dengan variabel X ke-i yang bebas dari pengaruh variabel-variabel X ke-j; X ke-k; . . .; dan X ke-p.

1. Korelasi parsial order satu

Koefisien korelasi parsial order satu pada model persamaan regresi:

#

=



0 +



1 X1 +



2 X3. dapat diuraikan menjadi:

(1). r YX1.X2 koefisien korelasi parsial antara Y & X1 jika X2 pengaruhnya konstan

(2). r YX3.X1 koefisien korelasi parsial antara Y & X2 jika X1 pengaruhnya konstan

(3). r X1X3.Y koefisien korelasi parsial antara X1 & X2 jika Y pengaruhnya konstan

Perhitungan nilai-nilai koefisien korelasi parsial oder satu untuk tiga variabel dari persamaan di atas, didasarkan pada nilai-nilai koefisien korelasi sederhana atau korelasi order nol. Koefisien korelasi parsial oder satu mempunyai persamaan:

[3.60a]. r  YX1.X2 = ) 1 ( ) 1 ( 2 2 2 1 ₂ 2 1 2 1  X   X  YX   X   X  YX  YX  r  r  r  r  r 

−

−

−

nilai X2 yang konstan

[3.60b]. r YX3.X1 = ) 1 ( ) 1 ( 1 2 2 1 2 2 1 1 2  X   X  YX   X   X  YX  YX  r  r  r  r  r 

−

−

−

nilai X1 yang konstan

[3.60c]. r X1X3.Y = ) 1 ( ) 1 ( 2 1 2 ₂ 2 1 1 2 1 YX  YX   X  Y  YX   X   X  r  r  r  r  r 

−

−

−

nilai Y yang konstan Dari persamaan [3.60a sd 3.60c] di atas dengan pengertian bahwa:

1) r YX1 adalah koefisien korelasi sederhana antara Y dengan X1; 2) r YX2 adalah koefisien korelasi sederhana antara Y dengan X2; dan 3) r X1X2 adalah koefisien korelasi sederhana antara X1 dengan X3.

 Apabila nilai koefisien korelasi sederhana diketahui besarnya sehingga analisis korelasi parsial oder satu dari persamaan regresi tiga variabel di atas menjadi:

[3.61a]. r YX1.X2 = ) 1 ( ) 1 ( 2X2 21 2 X2 1 X2 1  X   X  Y   X  Y  YX  r  r  r  r  r 

−

−

− [3.61b]. r YX3.X1 = ) 1 ( ) 1 ( 2_X1 2_{1 2} X2 1 X1 2  X   X  Y   X  Y  YX  r  r  r  r  r 

−

−

− [3.61c]. r X1X3.Y = ) 1 ( ) 1 ( 22 2 X1 X2 X1 2 ! YX  Y  Y  Y   X   X  r  r  r  r  r 

−

−

−

Beberapa interprestasi yang dapat diungkapkan dari persamaan (3.61a sd 3.61c) di atas adalah sebagai berikut:

1). Dalamr YX1.X2; jikar YX1 = 0, maka r YX1.X2  tidak akan = 0, kecuali apabila r YX2 atau

r X1X2 = 0 atau kedua-duanya = 0.

2). Dalamr YX1.X2; jika r YX1 = 0, di mana r YX2  serta r X1X2

&

0, dan selain itu

kedua-duanya mempunyai tanda yang sama (+ atau -), maka r YX1.X2 mungkin

akan negatif.

3). Sedangkan, dalamr YX1.X2 jika r YX1 = 0, di mana r YX2serta r X1X2

&

0, dan selain itu

Sebagai misal: Y produksi padi per hektar, X1  curah hujan dan X2  temperatur udara.

Diumpamakan Y = 0, yaitu bahwa tidak ada hubungan antara jumlah curah hujan dengan produksi padi, atau dengan kata lain bahwa produksi padi tidak dipengaruhi oleh curah hujan. Selanjutnya, diasumsikan pula bahwar YX2 bertanda positif (+) dan r X1X2bertanda

negatif (-), maka nilai r YX1.X2 akan bertanda positif (+) dan yaitu dengan anggapan bahwa

suhu konstan, maka akan terjadi korelasi yang positif antara produksi padi per hektar dengan curah hujan.

4). Bahwa r X1X2  dan r YX1  (serta penduga yang setara) tidak perlu mempunyai tanda

yang sama.

5). Dalam analisis regresi dua variabel bebas X, maka nilair YX1.X2 akan berkisar antara

0 dan 1. Nilai yang sama akan didapat juga dari analisis korelasi parsial yaitu: 0

+

r YX1

2

 +r YX2 2

-r YX1r YX2r X1X2

+

 1

(nilai dalam tanda pertidaksamaan disebut dengan koefisien determinasi ganda (r 2), akan dibicara kemudian).

6). Dalamr YXi.Xj yang bernilai negatif maka disamakan dengan nokl (0).

3.13.3 Koefisien Deterninasi

Koefisien determinasi R2 dapat dihitung langsung dari data bersamaan dengan koefisien regresi bi. Kegunaan dari Koefisien determinasi R2 adalah untuk mengukur tingkat

ketepatan yang paling baik dari analisis regresi.

Jika data observasi dapat tepat pada garis atau bidang regresi yang diestimasi, maka dikatakan terjadi kecocokan garis atau bidang regresi dengan sepurna, dan nilai koefisien determinasi akan maksimum yaitu R2 = 1.

Dalam kenyataan terhadap data pengamatan akan terjadi penyimpangan dengan garis atau bidang regresi penduga yang dikodekan dengan ei. Di dalam analisis regresi

dengan metode kuwadrat terkecil (OLS) diusahakan supaya nilai

)

ei sekecil mungkin

mendekati nol atau nilai koefisien determinasi semaksimum mungkin mendekati satu. Koefisien determinasi berganda R2 dengan rumus umum seperti berikut:

[3.62] R2 = Total   Kuadrat   Jumlah  gresi  Kuadrat   Jumlah Re

Koefisien determinasi berganda R2  dari regresi tiga variabel atau untuk regresi dengan dua variabel bebas X (X1dan X2) dengan model persamaan regresi seperti

#

=



0 +



1

X1 +



2 X3. dapat didefinisikan sebagai berikut :

[3.63] R2 =

∑

∑

∑

+

2 2 2 1 1 i  y  y  x b  y  x b _{i i i i}

Untuk regresi p + 1 variabel atau dengan p variabel bebas X (X1, X2, X3, . . ., Xp) dengan

model persamaan regresi seperti

#

=



0 +



1 X1 +



2 X2 + . . . +



p Xp  dapat

didefinisikan sebagai berikut : [3.64] R2 =

∑

∑

∑

∑

+

+

+

2 2 2 1 1 ... i  y  y  x b  y  x b  y  x b _{i i i i k   pi i}

Kelanjutan uraian koefisien determinasi berganda dan modifikasinya akan dibahas pada hal-hal selanjutnyaI.

Nilai harapan (E) koefisien determinasi R2yang ditulis dengan E(R2) yang sering disebut dengan koefisien determinasi yang disesuaikan atau koefisien determinasi terkoreksi,

[3.65] E(R2) = (1 ₂) 2  y e  E  σ σ

−

= 1 -) 1 /( ) /( 2 2

−

−

∑

∑

n  y k  n e = 1 -k  n n

−

−

1

∑

∑

2 2  y e = 1 -k  n n

−

−1

_(1-R2 ) = 1 -k  n n

−

−1

 ₊ k  n n

−

−1

_R2 = k  n n k  n

−

+

−

−

1  + k  n n

−

−1

_R2 = k  n k 

−

−

1  + k  n n

−

−1

_R2

Dari penyelesaian persamaan [3.65] di atas maka didapatkan bahwa nilai harapan E(R2) yang disebut dengan nilai koefisien determinasi terkoreksi yang biasa ditulis dengan _R2_{sehingga persamaan terakhir di atas dapat ditulis menjadi:}

[3.66]  _R2 ₌ k  n k  k  n n  R

−

−

+

−

−

1 1 2 = k  n k  k  n n  R

−

−

−

−

−

1 1 2

Penyelesaian selanjutnya dari persamaan [3.66] akan menjadi: [3.67]  _R2 ₌ k  n k  k  n kR kR  R nR

−

−

−

−

−

+

−

2 2 2 1 2 = k  n k   R k  n k  k  n k  n  R

−

−

+

−

−

−

−

−

) 1 ( 1) ( 2 2 = R2 - 1(1  R2) k  n k 

−

−

−

3.14 Contoh Analisis dan Uraiannya

 Agar dapat memahami uraian di atas dan dapat menentukan nilai koefisien regresi penduga atau koefisien regresi biyaitu nilai- nilai b0, b1, dan b2, maka diberikan contoh

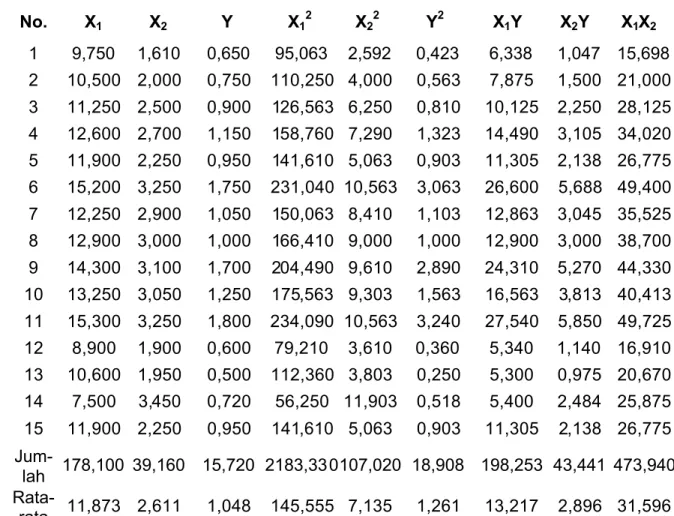
olahan seperi di bawah ini, yang datanya terdiri dari dua variabel bebas X (prediktor = regresor) yaitu X1 dan X2 seperti pada Tabel 3.3.

Tabel 3.3. Pengamatan Data Rregresi Dua Variabel Bebas X dan Satu Variabel Y

No. X1 X2 Y X12 X22 Y2 X1 Y X2 Y X1X2

1 9,750 1,610 0,650 95,063 2,592 0,423 6,338 1,047 15,698 2 10,500 2,000 0,750 110,250 4,000 0,563 7,875 1,500 21,000 3 11,250 2,500 0,900 126,563 6,250 0,810 10,125 2,250 28,125 4 12,600 2,700 1,150 158,760 7,290 1,323 14,490 3,105 34,020 5 11,900 2,250 0,950 141,610 5,063 0,903 11,305 2,138 26,775 6 15,200 3,250 1,750 231,040 10,563 3,063 26,600 5,688 49,400 7 12,250 2,900 1,050 150,063 8,410 1,103 12,863 3,045 35,525 8 12,900 3,000 1,000 166,410 9,000 1,000 12,900 3,000 38,700 9 14,300 3,100 1,700 204,490 9,610 2,890 24,310 5,270 44,330 10 13,250 3,050 1,250 175,563 9,303 1,563 16,563 3,813 40,413 11 15,300 3,250 1,800 234,090 10,563 3,240 27,540 5,850 49,725 12 8,900 1,900 0,600 79,210 3,610 0,360 5,340 1,140 16,910 13 10,600 1,950 0,500 112,360 3,803 0,250 5,300 0,975 20,670 14 7,500 3,450 0,720 56,250 11,903 0,518 5,400 2,484 25,875 15 11,900 2,250 0,950 141,610 5,063 0,903 11,305 2,138 26,775 Jum-lah 178,100 39,160 15,720 2183,330 107,020 18,908 198,253 43,441 473,940 Rata-rata 11,873 2,611 1,048 145,555 7,135 1,261 13,217 2,896 31,596 3.14.1 Perhitungan nilai JK- JHK

Perhitungan nilai JK- JHK dari data tabel di atas dapat dilihat di bawah ini. Perhitungan nilai JK seperti:

JK Y =

(y

2 =

(Y

2 - ((Y)2/n = 18,908 - (5,720)2/15 = 2,4338 JK X1 =

(x

12 =

(X

12 - ((X)2/n = 2183,330 - (178,100)2/15 = 68,6893 JK X2 =

(x

22 =

(X

22 - ((X)2/n = 107,020 - (39,160)2/15 = 4,7859

Perhitungan nilai JHK seperti: JHK X1Y =

(

x1y =

(

X1Y -

(

X1

(

Y/n = 198,253 - (178,100)(5,720)/15 = 11,6037 JHK X2Y =

(

x2y =

(

X2Y -

(

X2

(

Y/n = 43,441 - (39,160)(5,720)/15 = 2,4008 JHK X1X2 =

(

x1x2 =

(

X1X2 -

(

X1

(

X2/n = 473,940 - (178,100) (39,160)/15 = 8,9803

3.14.2 Perhitungan untuk mencari nilai b1, b2, dan b0seperti berikut ini:

Perhitungan untuk mencari nilai b1, b2, dan b0 didasarkan pada nilai JK-JHK

b1 =

(

)

2 2 1 2 1 2 1 1 1 2  X   X   JHK   X   JK   X   JK   X   X   JHK   X   JK  Y   X   JHK   X   JK 

−

−

=

(

)(

) (

)

(

)

(

)

(

) (

)

2 9803 , 8 78589 , 4 6893 , 68 9803 , 8 6893 , 68 6037 , 11 78589 , 4

−

−

= 0,136940 b2 =

(

)

2 2 1 2 1 2 1 2 2 1  X   X   JHK   X   JK   X   JK   X   X   JHK   X   JK  Y   X   JHK   X   JK 

−

−

=

(

)(

) (

)(

)

(

)

(

) (

)

2 9803 , 8 7859 , 4 6893 , 68 9803 , 8 7859 , 4 4008 , 2 6893 , 68

−

−

= 0,244691 b0 = Y - b1 X 1 - b2 X 2 = 1,048 - (0,136940) (11,873) - (0,244691) (2,611) = -1,216739

Sehingga persamaan Regresi bergandanya menjadi:

#

= b0 + b1 X1 + b2 X2

#

= -1,216739 + 0,136940 X1  - 0,244691 X2

Selanjutnya, dilakukan pengujian terhadap regresi linier berganda terutama

pengujian terhadap nilai-nilai koefisien regresi berganda (bi) serta pengujian terhadap

bidang regresi.

Dalam pengujian regresi linier berganda terdapat tiga macam uji yaitu:

1). Uji simultan atau uji F atau uji ragam regresi atau uji varians regrsi;

2). Uji parsial atau uji koefisien regresi berganda atau uji terhadap bi atau uji t; dan