LANDASAN TEORI
2.1 Teknik Simulasi
Teknik simulasi menjadi pilihan kedua ketika cara analisis lain tidak mungkin atau sulit dilakukan. Berbagai kombinasi dan alternatif dapat dipelajari melalui simulasi sebelum penerapannya di lapangan. Hal ini akan mengurangi terjadinya kesalahan yang berakibat biaya yang sangat besar dalam penerapannya. Simulasi merupakan cara menampilkan kembali kondisi suatu keadaan dalam bentuk model untuk dipelajari, diuji, dan sebagainya. Terdapat definisi beberapa ahli tentang simulasi: (Suharianto,2007)
a. Banks (1998), Simulasi adalah tiruan dari proses dunia nyata atau sistem. Simulasi menyangkut pembangkitan proses serta pengamatan dari proses untuk menarik kesimpulan dari sistem yang diwakili.
b. Nailor (1996) dalam Rubinstein & Mclamed (Mclmed 1998), Simulasi adalah teknik numerik untuk melakukan eksperimen pada komputer, yang melibatkan jenis matematika dan model tertentu yang menjelaskan prilaku bisnis atau ekonomi pada suatu periode waktu tertentu.
c. Borowski & Borwein (1989), Simulasi adalah teknik untuk membuat konstruksi model matematika untuk suatu proses atau situasi dalam rangka menduga secara karakteristik atau menyelesaikan masalah berkaitan dengannya dengan mengunakan model yang diajukan.
Jadi simulasi mempelajari atau memprediksi sesuatu yang belum terjadi dengan cara membuat model sistem yang dipelajari dan selanjutnya mengadakan eksperimen secara numerik dengan mengunakan komputer.
Pada umumnya dibutuhkan sebuah komputer dengan piranti lunak untuk simulasi. Simulasi membuat seseorang seolah-olah berinteraksi dengan dunia nyata, dimana sebenarnya ia sedang berinteraksi dengan imitasinya. Simulasi pada penggunaannya dibatasi untuk model yang mempunyai karakteristik nyata sehingga dapat menghasilkan inti dari operasi yang sebenarnya. Ada beberapa keuntungan yang dapat diperoleh dengan memanfaatkan simulasi yaitu menghemat waktu, mengkoreksi kesalahan-kesalahan perhitungan, dan mudah diperbanyak.
Simulasi menurut tekniknya dapat dibedakan menjadi dua, yaitu simulasi secara langsung (physical simulation) dan simulasi dengan bantuan komputer (computer
simulation). Computer simulation biasanya digunakan apabila tidak dapat digunakan
secara langsung di lapangan. Simulasi ini diikuti dengan penggunaan komputer untuk mengkombinasi komponen-komponen dari model masalah dan melakukan suatu analisis untuk mengetahui akibat dari hubungan komponen-komponen tersebut.
Diperlukan langkah-langkah yang sederhana tapi sistematis agar penyusunan program simulasi dapat berjalan dengan baik. Untuk memecahkan suatu persoalan, hendaknya persoalan tersebuat dianalisis dan diformulasikan terlebih dahulu.
Analisis persoalan ini menyangkut hal-hal sebagai berikut:
Asal atau latar belakang persoalan; menentukan apa yang menjadi persoalan sebenarnya. Dapat saja persoalan itu hanya merupakan bagian kecil dari persoalan yang sesungguhnya. Perlu dicari inti dari persoalan tersebut.
Materi yang ditemukan dalam persoalan tersebut perlu didiskusikan dan ditelaah secara cermat agar materi persoalan yang ada dapat ditangani semuanya.
2.2 Algoritma
Penemu kata algoritma adalah seorang ahli matematika dari Uzbekistan yang bernama Abu Abdullah Muhammad Ibn Musa al-Khwarizmi (770-840). Di literatur barat dia lebih terkenal dengan sebutan Algorizm. Panggilan inilah yang kemudian dipakai untuk menyebut konsep algorithm yang ditemukannya. (Wahono, 2003).
Dalam bahasa Indonesia kita kemudian menyebutkannya sebagai algoritma. Algoritma adalah kunci dari bidang ilmu komputer, karena banyak bidang di bawah ilmu komputer yang lahir berdasarkan konsep algoritma ini. Pada hakekatnya algoritma juga adalah kunci dari kehidupan kita.
Kita dapat mendefinisikan algoritma sebagai suatu logika, metode dan tahapan (urutan) sistematis yang digunakan untuk memecahkan suatu permasalahan. Secara formal, berdasarkan Kamus Besar Bahasa Indonesia (Balai Pustaka, 1988), algoritma didefinisikan sebagai urutan logis pengambilan keputusan untuk pemecahan masalah.
2.2.1 Beda Algoritma dan Program
Program adalah kumpulan instruksi komputer, sedangkan metode dan tahapan sistematis dalam program adalah algoritma. Program ditulis dengan menggunakan bahasa pemrograman. Jadi dapat dikatakan bahwa program adalah merupakan implementasi dari bahasa pemrograman.
Beberapa pakar memberi formula bahwa program adalah gabungan dari struktur data dan algoritma. Bagaimanapun juga struktur data dan algoritma berhubungan sangat
erat pada sebuah program. Algoritma yang baik tanpa pemilihan struktur data yang tepat akan membuat program menjadi kurang baik, demikian juga sebaliknya.
2.3 Algoritma Genetik
Algoritma Genetik adalah sebuah algoritma pencarian solusi yang dibuat dengan menerapkan mekanisme evolusi genetika makhluk hidup dalam dunia biologi. Algoritma Genetik memiliki konteks yang lebih sederhana, karena tidak sekompleks dan serumit evolusi genetik dalam dunia biologi. Dalam dunia biologi, semua makhluk hidup memiliki sel, dan setiap sel terdiri dari kromosom-kromosom (susunan DNA) yang menjadi “blueprint” dari makhluk hidup tersebut.
Pada algoritma ini, teknik pencarian dilakukan sekaligus atas sejumlah solusi yang mungkin yang dikenal dengan istilah populasi. Individu yang terdapat dalam suatu populasi disebut dengan istilah kromosom. Kromosom ini merupakan suatu solusi yang masih berbentuk simbol. Populasi awal dibangun secara acak, sedangkan populasi berikutnya merupakan hasil evolusi kromosom-kromosom melalui iterasi yang disebut dengan istilah generasi. Pada setiap generasi, kromosom akan melalui proses evaluasi dengan menggunakan alat ukur yang disebut dengan fungsi fitness. Nilai fittnes dari suatu kromosom akan menunjukan kualitas kromosom dalam populasi tersebut. Generasi berikutnya dikenal dengan istilah anak (off-spring) terbentuk dari gabungan 2 kromosom generasi sekarang yang bertindak sebagai induk (parent) dengan menggunakan operator penyilangan (crossover). Selain operator penyilangan, suatu kromosom dapat juga dimodifikasi dengan menggunakan operator mutasi. Populasi generasi yang baru dibentuk dengan cara menyeleksi nilai fitness dari kromosom induk (parent) dan nilai fitness dari kromosom anak (offspring), serta menolak
kromosom-
kromosom yang lainnya sehingga ukuran populasi (jumlah kromosom dalam suatu populasi) konstan. Setelah melalui beberapa generasi, maka algoritma ini akan konvergen ke kromosom terbaik.
2.3.1 Implementasi Algoritma Genetik
Implementasi Algoritma Genetik secara umum memiliki tahapan proses (algoritma) sebagai berikut:
a. Membuat populasi awal yang terdiri dari n buah kromosom (kandidat solusi untuk masalah yang ada)
b. Menghitung fitness cost setiap kromosom dalam populasi.
c. Melakukan pengulangan proses seleksi, crossover, mutasi hingga n buah kromosom baru (offspring) terbentuk.
d. Mengganti populasi lama dengan populasi yang baru terbentuk. e. Kembali ke langkah (b).
Namun sebelum melakukan implementasi, ada beberapa hal penting yang harus dilakukan, yaitu:
a. Memilih jenis pengkodean suatu masalah ke Algoritma Genetik. b. Menentukan operator genetik yang digunakan.
c. Melakukan seleksi yang diperlukan.
Setelah menentukan hal-hal di atas, Algoritma Genetik dapat diimplementasikan ke dalam program.
2.3.1.1 Representasi Kromosom dalam Biner
Sebuah nilai solusi yang dihasilkan dalam algoritma genetik disebut dengan kromosom. Kromosom tersususn atas gen-gen yang merupakan representasi nilai variabel dalam suatu fungsi yang ingin dicari solusinya. Kromosom dapat dibentuk dari
numerik, biner ataupun karakter. Representasi kromosom dalam bentuk biner adalah bentuk yang banyak digunakan karena mempermudah pemrograman didalam proses algoritma genetika seperti crossover dan mutasi. Sebelum diproses dalam algoritma genetika, solusi yang dibangkitkan baik dalam bentuk integer atau float harus dirubah dulu ke dalam bentuk biner. Demikian pula sebaliknya setelah proses-proses dalam algoritma genetika selesai maka nilai kromosom biner tersebut harus dirubah kembali ke bentuk semula yaitu berupa bilangan integer atau float.
Sebagai contoh adalah merubah bilangan integer 23 ke dalam bentuk biner dengan panjang biner n = 5:
Langkah-langkah:
1. Lakukan proses pembagian bilangan dengan 2 sebanyak 5 kali iterasi, dan dapatkan nilai modulusnya:
23 dibagi 2 sama dengan 11 sisa 1 11 dibagi 2 sama dengan 5 sisa 1 5 dibagi 2 sama dengan 2 sisa 1 2 dibagi 2 sama dengan 1 sisa 0 1 dibagi 2 sama dengan 0 sisa 1
2. Dapatkan nilai binernya dengan cara menyimpan nilai modulus dimulai dari bawah atau dari pembagian yang terakhir.
Maka biner untuk 23 adalah: 10111
Pengkodean Bilangan Floating, prinsip untuk merubah bilangan float ke biner adalah dengan merubah bilangan float tersebut menjadi bilangan integer terlebih dahulu, setelah itu bilangan integer tersebut baru dirubah dalam biner. Untuk mengubah dari bilangan float ke integer adalah dengan mengalikan bilangan tersebut dengan 10m
dimana m = jumlah angka dibelakang koma dari bilangan float yang akan dirubah ke biner. Jika ruang solusi dari algoritma genetika adalah antara a≤x≤b dimana x adalah bilangan float, maka :
1
2
n−< −
(
b a
) *10
m≤
2
n−
1
Demikian pula proses sebaliknya untuk merubah dari bilangan biner ke bentuk bilangan float maka proses pertama kali adalah dengan mendapatkan nilai integer dari bilangan biner tersebut baru kemudian dihitung nilai floatnya.
Rumus yang dapat digunakan untuk merubah bilangan biner ke float adalah:
(
)
integer *
2
n1
b a
x a
= +
−
−
Dimana integer adalah nilai int dari bilangan biner yang akan dirubah. 2.3.1.2 Operator-Operator Genetik dalam Algoritma Genetik
Langkah berikutnya adalah menentukan operator genetik yang digunakan dalam Algoritma Genetik. Penentuan operator genetik ini sangat bergantung pada jenis pengkodean yang dipilih. Dua buah operator genetik yang paling umum dan sering digunakan dalam implementasi Algoritma Genetik adalah:
a. Crossover (Kawin Silang)
Crossover dilakukan dengan cara menukar bagian kecil dari dua buah
kromosom (parent) yang berbeda sehingga diperoleh kromosom baru yang masih memiliki sifat-sifat kromosom parent-nya. Cara melakukan crossover dapat dibagi berdasarkan jumlah posisi yang dipilih, yaitu single-point crossover dan two-point
membagi kromosom menjadi dua bagian. Satu bagian dari kromosom di kromosom ditukarkan dengan kromosom lain yang juga telah dibagi menjadi dua.
Contoh single-piont crossover :
Kromosom A : 1001011 | 01110101 Kromosom B : 1110100 | 01011011
Pada contoh ini, posisi acak yang dipilih jatuh pada bit ke-8 sehingga kromosom terbagi menjadi dua, yaitu bit 1-7 dan 8-15. Bit 8-15 dari kedua kromosom tersebut ditukar sehingga menghasilkan dua kromosom baru sebagai berikut:
Kromosom A : 1001011 | 01011011 Kromosom B : 1110100 | 01110101
Two-point crossover pada prinsipnya sama dengan single-point crossover.
Bedanya, pada two-point crossover, dua buah posisi yang dipilih secara acak, sehingga membagi kromosom menjadi tiga bagian. Tujuan dari two-point
crossover adalah untuk menukar bagian yang berada di antara dua posisi acak
tersebut (bagian tengah kromosom). Contoh two-point crossover:
Kromosom A : 10010 | 110111 | 0101 Kromosom B : 11101 | 000101 | 1011
Pada contoh diatas, posisi acak jatuh pada bit ke-6 dan bit ke-11. Bagian yang ditukar adalah bit 6-11 yang berada di tengah kromosom. Hasil pertukaran menghasilkan kromosom berikut:
Kromosom A : 10010 | 000101 | 0101 Kromosom B : 11101 | 110111 | 1011
Selain dua metode di atas, ada satu metode yang disebut uniform crossover, di mana pertukaran dilakukan dengan cara menukar bit-bit kedua kromosom parent secara acak.
b. Mutation (Mutasi)
Mutasi adalah perubahan nilai gen (allele) dalam kromosom secara permanen sehingga kromosom tersebut mengalami perubahan bentuk. Mutasi dilakukan dengan cara memilih satu atau beberapa posisi gen dalam kromosom dan kemudian mengganti nilainya. Pada binary encodings, mutasi dilakukan dengan meng-invert nilai gennya, yaitu 0 diganti menjadi 1 dan sebaliknya.
Contoh mutasi:
Kromosom A : 100100001010101 Kromosom A* : 100000101001111
Kromosom B : 1.235 2.215 1.525 0.223 5.412 Kromosom B* : 1.235 2.637 1.525 0.223 5.883
Dalam kebanyakan aplikasi Algoritma Genetik, dua operator ini tidak dipilih untuk digunakan salah satunya saja, tetapi digunakan secara bersama-sama. Keseimbangan yang tepat dalam penggunaan crossover, mutasi, dan seleksi merupakan bagian yang sangat penting dalam Algoritma Genetik. Keseimbangan ini juga sangat tergantung pada pengkodean dan fungsi untuk menentukan fitness
cost.
2.3.1.3 Metode-Metode Seleksi
Seleksi akan menentukan individu-individu mana saja yang akan dipilih untuk dilakukan rekombinasi dan bagaimana offspring terbentuk dari individu-individu terpilih tersebut. Langkah pertama yang dilakukan dalam seleksi ini adalah pencarian nilai
fitness. Masing-masing individu dalam suatu wadah seleksi akan menerima probabilitas
reproduksi yang tergantung pada nilai objektif dirinya sendiri terhadap nilai objektif dari semua individu dalam wadah seleksi tersebut. Nilai fitness inilah yang nantinya akan digunakan pada tahap-tahap seleksi berikutnya. Metode-metode seleksi antara lain:
a. Roulette Wheel Selection
Dalam metode ini, kromosom-kromosom yang ada dalam populasi ditempatkan ke dalam roda yang disebut “roulette wheel”. Setiap kromosom menempati potongan roda dengan ukuran yang proposional dengan fitness cost yang dimilikinya. Putaran dilakukan sebanyak n kali, dan pada setiap putaran, kromosom yang berada di bawah penanda roda dipilih sebagai parent untuk generasi berikutnya. Metode ini merupakan metode yang digunakan Holland pada Algoritma Genetik yang dikembangakan olehnya.
Kelemahan utama metode ini adalah bila terdapat satu kromosom yang memiliki fitness cost yang tinggi sekali, sebagai contoh 90% dari keseluruhan roda, maka kromosom-kromosom yang lain hanya menempati 10% dari keseluruhan roda. Akibat dari kondisi ini, setiap putaran roda kemungkinan besar menghasilkan kromosom yang sama sehingga populasi baru hanya dihuni oleh kromosom yang sama. Kondisi ini disebut sebagai “premature convergence” (kenvergensi dini).
b. Elitism
Metode ini pertama kali diperkenalkan oleh Kenneth De Jong (1975). Dalam metode ini beberapa gen terbaik dari setiap generasi diambil dan disimpan. Tujuan metode ini adalah mencegah hilangnya gen-gen terbaik karena tidak terpilih untuk
melakukan crossover atau mutasi. Banyak penelitian yang menemukan bahwa metode ini menigkatkan kinerja Algoritma Genetik secara signifikan.
c. Rank Selection
Metode ini merupakan alternatif untuk mencegah terjadinya konvergensi dini yang terlalu cepat. Dalam metode ini, kromosom-kromosom dalam populasi dirangking berdasarkan fitness cost yang dimiliki.
Pemilihan kromosom tidak didasarkan pada nilai fitness cost, namun didasarkan pada nilai rangking yang diberikan. Hal ini bertujuan untuk menguragi perbedaan nilai yang besar seperti yang dapat terjadi pada metode Roulette Wheel
Selection. d. Tournament Selection
Dalam metode ini, dua buah kromosom dipilih secara acak dari populasi. Sebuah angka r dipilih secara acak dari angka-angka di antara 0 dan 1. Sebuah parameter k ditentukan (misalnya k = 0.75). Jika r < k, maka kromosom dengan
fitness cost yang lebih baik dipilih, dan jika sebaliknya, kromosom dengan fitness cost lebih rendah yang dipilih. Kedua kromosom tersebut kemudian dikembalikan
ke populasi dan dapat dipilih lagi.
e. Steady-State Selection
Dalam metode ini, hanya sebagian kecil kromosom dari populasi yang diganti dalam setiap generasi. Biasanya kromosom-kromosom yang memiliki fitness cost rendah diganti dengan kromosom-kromosom baru hasil crossover dan mutasi dari kromosom-kromosom dengan fitness cost tinggi. Metode ini sering digunakan dalam rule-based system dimana proses pembelajaran memiliki peran penting dan
semua anggota populasi secara bersama-sama (tidak secara individual) memecahkan masalah yang ada.
Secara umum, diagram alir algoritma genetik sederhana seperti terlihat pada Gambar 2.1.
Gambar 2.1 Diagram alir algoritma genetik sederhana
2.3.1.4 Cara Kerja Algoritma Genetik pada Optimasi Penempatan Fasilitas
Dalam penentuan lokasi penempatan suatu fasilitas diantara n fasilitas lainnya, fasilitas tersebut haruslah ditempatkan sedemikian rupa sehingga total biaya yang dikeluarkan antara fasilitas-fasilitas lama dan fasilitas baru bisa seminimum mungkin.
Untuk meminimumkan total biaya digunakan rumus:
2 2 1 ( ) ( ) n i i i i C W X X Y Y = =
∑
− + − (2.1) Dengan :
C = total biaya
i
W = bobot fasilitas lama ke-i
i
X = absis koordinat fasilitas lama ke-i
i
Y = ordinat koordinat fasilitas lama ke-i
X = absis koordinat fasilitas baru
Y = ordinat koordinat fasilitas baru
Apabila diketahui 17 pos pemadam kebakaran dengan koordinat dan bobot seperti pada Tabel 2.1.
Tabel 2.1 Lokasi Fasilitas yang Sudah Ada Koordinat Lokasi ke Nama Fasilitas X Y Bobot 1 Sudin 21 29 2 2 Fatmawati 28 36 5 3 Jagakarsa 33 19 6 4 Psr.Minggu 42 36 3 5 Srg. Sawah 39 8 9 6 Pejaten 43 28 2 7 Mampang Prp. 36 43 4 8 Cipete 26 39 7 9 Tebet 41 41 3 10 Casablanka 44 49 5 11 Kalibata 44 39 8 12 Kebayoran Br. 28 39 1 13 Tanah Kusir 20 36 7 14 Pesanggrahan 15 41 2 15 Cipulir 21 44 4 16 Grogol Utara 22 51 5 17 Walikota 33 39 1
Representasi kromosom dilakukan dengan menggunakan representasi biner, dengan dua variabel input, yaitu absis (X) dan ordinat (Y). Range untuk X adalah absis terkecil dari lokasi fasilitas yang sudah ada sampai X terbesar adalah absis terbesar dari lokasi fasilitas yang sudah ada [15 44]. Demikian pula, range untuk Y adalah ordinat terkecil dari lokasi fasilitas yang sudah ada sampai ordinat terbesar dari lokasi fasilitas yang sudah ada [8 51].
a. Representasi Solusi
Kromosom v merupakan representasi dari variabel x yang berbentuk string biner. Sedangkan panjang setiap kromosom tergantung pada presisi yang diinginkan. Secara umum, misalkan selang yang diinginkan untuk variabel x adalah [a b], dengan presisi n, maka panjang kromosom L dapat dirumuskan sebagai:
2
log[(
)10
n1]
i
L
=
⎡
⎢
b a
−
+
⎤
⎥
Sedangkan nilai x dapat dirumuskan sebagai:
[( ) / (2L 1)]*
x a= + b a− − v
Karena ada dua variabel, maka satu kromosom terdiri atas dua gen. Gen1 mewakili X dan Gen2 mewakili Y. Dalam kasus ini presisi yang diinginkan adalah dua angka desimal, maka panjang kromosom untuk Gen1 dan Gen2 adalah:
Panjang Gen_1 (L1) = ⎡⎢2log[(44 15) *10− 2+1]⎤⎥ =12
Panjang Gen_2 (L2) = ⎡⎢2log[(51 8) *10− 2 +1]⎤⎥=12 Sehingga panjang kromosom (L) = 12+12 = 24.
1 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 0 1 1 0 0 0 1 Maka : Gen_1 = 1 0 0 1 1 0 1 0 0 1 1 1 V1 = 2471 X = a+[(b a− ) / (2L −1)]*v = 15 [(44 15) / (2+ − 12−1)]* 2471 32.4991453= Gen_2 = 0 0 0 1 1 0 1 1 0 0 0 1 V2 = 433 Y = 8 [(51 8) / (2+ − 12 −1)]* 433 12.54676435= Fungsi fitness yang digunakan adalah :
Fitness = 1
C; dengan C = total biaya (persamaan 2.1)
b. Penentuan Parameter
Yang disebut dengan parameter di sini adalah parameter kontrol algoritma genetika, yaitu: ukuran populasi (popsize), peluang crossover (Pc), dan
peluang mutasi (Pm). Nilai parameter ini ditentukan juga berdasarkan
permasalahan yang akan dipecahkan.
1. Untuk permasalahan yang memiliki kawasan cukup besar, De Jong merekomendasikan untuk nilai parameter kontrol:
(popsize; pc, pm) = (50; 0,6; 0,001)
2. Bila rata-rata fitness setiap generasi digunakan sebagai indikator, maka Grefenstete merekomendasikan:
(popsize; pc, pm) = (30; 0,95; 0,01)
3. Bila fitness dari individu terbaik dipantau pada setiap generasi, maka usulannya adalah:
(popsize; pc, pm) = (80; 0,45; 0,01)
2.4 Teori Tentang Kebakaran
Definisi Kebakaran adalah timbulnya bahaya api yang tidak diinginkan, yang dapat mendatangkan kerugian berupa material maupun jiwa (Soenarjo, 1985). Seperti yang diterangkan pada Bab I, kebakaran dapat terjadi secara tak terduga. Pada bangunan yang dihuni oleh banyak orang, potensi terjadinya kebakaran cendrung lebih besar. Apabila penghuni secara sadar atau tidak sadar mengabaikan perihal kemungkinan terjadinya kebakaran pada bangunannya maka bangunan berikut penghuninya telah terbahayakan oleh bahaya kebakaran.
2.4.1 Penyebab Kebakaran
Dapat dikatakan terdapat lima penyebab rawan kebakaran, yaitu: (Pangaribuan, 1997).
1. Dari segi konstruksi bangunan yang meliputi bahan bangunan, jenis partisi, instalasi, serta penempatan barang.
2. Sarana proteksi dan pengamanan jiwa tidak memadai, kemungkinan disebabkan peralatan cukup tapi tidak terawat atau tidak cukup dan tidak terawat.
3. Fungsi bangunan, restoran atau diskotek misalnya berbeda tingkat kerawanan dibanding perumahan. Sehingga jika berubah fungsi bangunan, seharusnya diubah pula peralatan pemadam kebakarannya.
4. Lingkungan bangunan. Pada lingkungan yang padat bangunan, jika satu bangunan terbakar, asap dan jilatan api bisa merembet ke bangunan sekelilingnya.
5. Sangat minimnya manajemen kebakaran yang dimiliki. Padahal suatu bangunan harus memiliki sumber daya manusia yang khusus menangani kebakaran. Disamping harus ada jadwal pemeriksaan dan pengujian, manajemen gedung harus membuat pola penanganan tetap atau prosedur tetap (protap).
2.4.2 Klasifikasi Daerah Rawan Kebakaran
Daerah rawan kebakaran dapat dikenali menurut penggunaan lahannya, yaitu: kawasan pemukiman, kawasan campuran, kawasan industri, dan kawasan perdagangan.
a. Tipologi I (Pemukiman)
Kawasan pemukiman yang rawan kebakaran dapat diidentifikasi dari penyebaran lingkungan permukiman kumuh. Oleh karena pemukiman kumuh ini memiliki tingkat hunian yang demikian padat, kondisi bangunan yang semi permanen dengan tata letak bangunan yang tidak teratur dan fasilitas umum (saluran drainase, sarana transportasi, pembuangan sampah dan sebagainya)
yang tidak memadai. Dengan berbagai kondisi daerah pemukiman ini umumnya rawan terhadap bahaya kebakaran.
b. Tipologi II (Kawasan Campuran)
Seperti halnya kegiatan industri, kuantitas bahan mudah terbakar pada kawasan campuran cukup tinggi. Dengan kondisi lingkungan fisiknya yang berlokasi di lingkungan kumuh maka akan mempercepat penjalaran api jika terjadi kebakaran.
Variabel lainnya adalah tenaga kerja yang ditampung untuk kegiatan ini. Jumlah dan perilaku mereka juga harus dipertimbangkan. Umumnya perilaku penghuni dan pekerja di lingkungan kawasan ini kurang peduli terhadap upaya pencegahan kebakaran. Adapun jenis kegiatan yang termasuk kategori ini seperti industri rumahan, percetakan, bengkel, dan lain-lain.
c. Tipologi III (Kawasan Industri)
Penggunaan lahan ini termasuk rawan kebakaran, karena kuantitas bahan mudah terbakarnya tinggi serta disebabkan oleh proses produksi dan kegiatan industri itu sendiri. Contohnya pabrik makanan dan minuman, serta pabrik kimia. Jika terjadi kebakaran, maka proses penjalarannya cepat.
d. Tipologi IV (Kawasan Perdagangan)
Dengan pertimbangan bahwa pengunjung terdiri dari berbagai macam lapisan masyarakat yang tingkat kepeduliannya beragam serta pertimbangan jumlah pengunjung yang besar maka mal dan daerah pertokoan di kawasan perdagangan menjadi tempat yang cukup rawan.
2.4.3 Daerah Rawan Kebakaran Jakarta Selatan
Wilayah Kotamadya Jakarta Selatan terdiri dari 10 kecamatan dan 65 kelurahan yang masih rawan kebakaran, khususnya tempat-tempat yang belum tertata, dengan ciri-ciri:
a. Jalan lingkungan sempit, banyaknya belokan serta badan jalan dimanfaatkan untuk parkir kendaraan.
b. Jarak antara bangunan hampir tidak ada dan tidak beraturan. c. Bangunan menggunakan bahan yang mudah terbakar. d. Perilaku masyarakat kurang kooperatif.
e. Menjangkau sumber air sangat sulit.
Tabel 2.2 Jenis Benda yang Terbakar Sepanjang Thn 2007 Sumber: Dinas Pemadam Kebakaran DKI Jakarta
Tabel 2.3. Daerah Padat Hunian Di Wilayah Kodya Jakarta Selatan Sumber: Dinas Pemadam Kebakaran DKI Jakarta
No Kelurahan Wilayah Rt/Rw
1. Kel. Karet Belakang - 02/04
2. Kel. Manggarai - 02/03
3. Kel. Manggarai Selatan - 010/02 4. Kel. Bukit Duri - 011/012
5. Kel. Pancoran - 01/03
6. Kel. Pejaten Timur - 01/010 7. Kel. Gandaria Utara - 02/011 8. Kel. Mampang Prapatan - 01/04 9. Kel. Cipete Utara - 03/04 10. Kel. Grogol Utara - 014/016 11. Kel. Kby Lama Utara - 06/09 12. Kel. Petukangan Utara - 04/09 13. Kel. Petukangan Selatan - 04/06
2.4.4 Perkiraan Kerugian Akibat Bahaya Kebakaran
Biaya kerugian terdiri atas kerugian langsung dan kerugian tidak langsung, sedangkan biaya pengeluaran terdiri dari biaya untuk meminimasi kerugian pada tingkat wajar, misalnya pengendalian kebakaran dan biaya untuk pertanggungjawaban kerugian. Kerugian-kerugian pokok adalah:
a. Kerugian jiwa/kematian
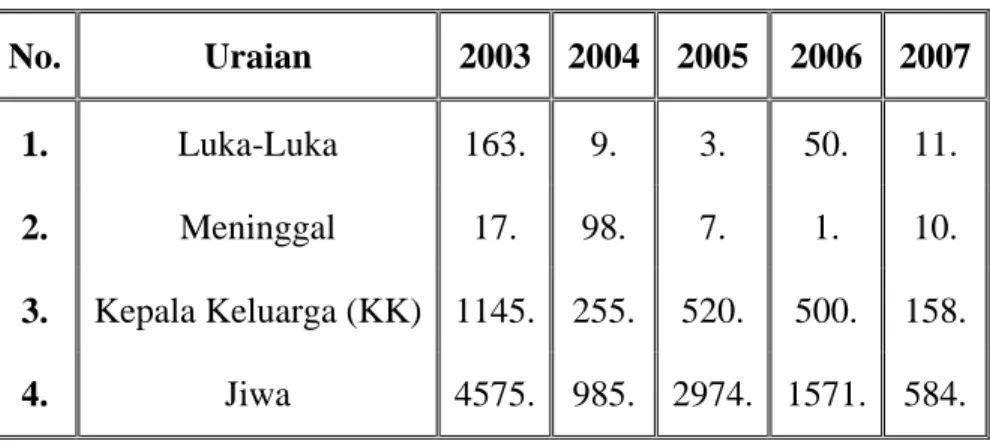
Tabel 2.4. Korban Jiwa Akibat Kebakaran Sepanjang Tahun 2003 s/d 2007 Sumber: Dinas Pemadam Kebakaran DKI Jakarta
2.5 Sumber Air
Salah satu unsur terpenting dalam pemadaman adalah tersedianya pasokan air dengan debit yang mencukupi. Pasokan air untuk keperluan pemadam kebakaran diperoleh dari sumber alam seperti kolam air, danau, sungai, jeram, sumur dalam dan saluran irigasi. Selain itu, pasokan air juga dapat diperoleh dari sumber buatan seperti tangki air, tangki gravitasi, kolam renang, air mancur, reservoir, mobil tangki serta hidran.
Permasalahan utama yang ditemui dalam upaya penjegahan kebakaran adalah sulitnya memperoleh pasokan air yang disebabkan terbatasnya sumber air, dan debit air yang tidak memadai dan juga petugas sering kali petugas kesulitan mencari sumber air yang tidak tersedia di dekat lokasi. Sehingga, proses pemadaman sering terhambat. Apalagi di pemukiman padat.
Kriteria daerah yang butuh hidran:
a. Daerah rawan kebakaran yang jauh dari sumber air b. Daerah padat penduduk
No. Uraian 2003 2004 2005 2006 2007
1. Luka-Luka 163. 9. 3. 50. 11.
2. Meninggal 17. 98. 7. 1. 10.
3. Kepala Keluarga (KK) 1145. 255. 520. 500. 158.
c. Daerah pemukiman kumuh (dimana bahan tempat tinggalnya mudah terbakar, dan tidak terjangkau fasilitas umum)
2.6 Model Rekayasa Piranti Lunak
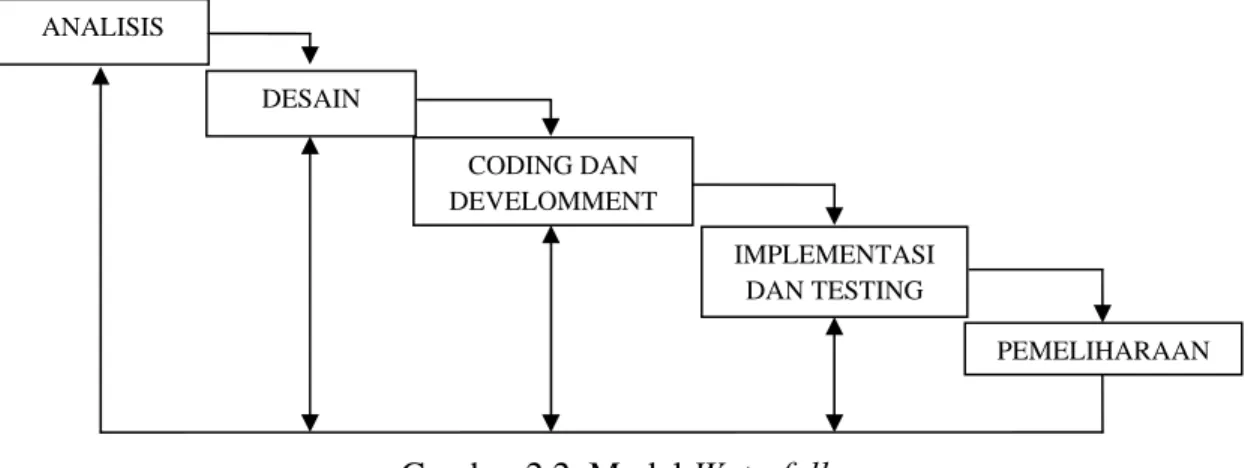
Model rekayasa piranti lunak yang dipakai penulis adalah sekuensial linear. Model ini biasa disebut juga model “air terjun” (waterfall).
Model ini merupakan sebuah pendekatan kepada perkembangan perangkat lunak yang sistematik dan sekuensial yang mulai pada tingkat dan kemajuan system pada seluruh analisis, desain, kode, pengujian dan pemeliharaan. Penjelasan tahapan dalam
Waterfall Model adalah sebagai berikut:
a. Analisis Kebutuhan
Proses pengumpulan kebutuhan diintensifkan dan difokuskan, khususnya pada perangkat lunak. Tujuan dari tahap ini adalah untuk mengetahui kebutuhan piranti lunak, sumber informasi piranti lunak, fungsi-fungsi yang dibutuhkan, kemampuan piranti lunak dan antar muka piranti lunak tersebut. b. Perancangan
Proses perancangan merupakan representasi kebutuhan ke bentuk perangkat luank yang dpat dinilai kualitasnya sebelum dilakukan pengkodean. Tahap ini meliputi perancangan struktur data, perancangan arsitektur piranti lunak, perancangan rincian prosedur dan perancangan user interface.
c. Pengkodean
d. Implementasi dan Pengujian
Setelah program aplikasi selesai dikode, program akan diujicobakan dan juga dilakukan pengujian. Pengujian dilakukan secara menyeluruh hingga semua perintah dan fungsi telah diuji sampai output yang dihasilkan oleh program sesuai dengan yang diharapkan.
e. Pemeliharaan
Pemeliharaan perangkat lunak dilakukan karena sering terjadinya perubahan dan peningkatan fungsi piranti lunak. Hal ini sesuai permintaan pemakai, maka piranti lunak yang telah selesai dibuat perlu dipelihara agar dapat mengantisipasi permintaan pemakai terhadap fungsi-fungsi baru. Bila terjadi perubahan berarti membalikan tahapan ke tahapan yang lebih awal. Untuk lebih jelasnya, tahapan ini dapat dilihat pada gambar 2.2.
Gambar 2.2. Model Waterfall
ANALISIS DESAIN CODING DAN DEVELOMMENT IMPLEMENTASI DAN TESTING PEMELIHARAAN
2.7 Eight Golden Rules
Untuk merancang sistem interaksi manusia dan komputer yang baik, harus memperhatikan delapan aturan emas dalam perancangan antarmukan, seperti: strive for consistency (konsisten dalam merancang tampilan), enable
frequent user to use shorcuts (memungkinkan pengguna menggunakan shortcuts
secara berkala), offer informative feed back (memberikan umpan balik yang informatif), design dialogs to yield closure (merancang dialog untuk menghasilkan keadaan akhir), offer simple error handling (memberikan penanganan kesalahan), permit easy reversal of actions (mengijinkan pembalikan aksi dengan mudah), support internal locus of control (mendukung pengguna menguasai sistem), dan reduce short-term memory load (mengurangi beban jangka pendek pada pengguna).