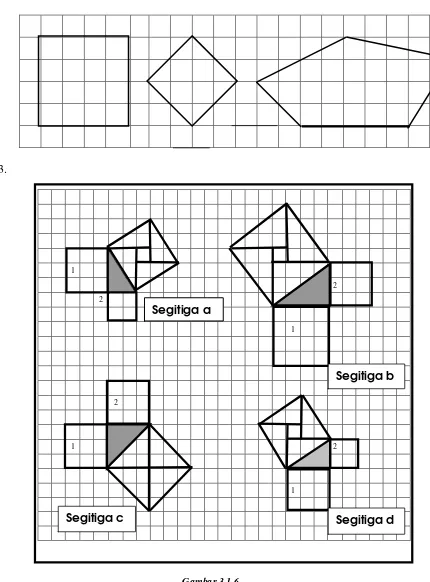
Menggunakan Teorema Pythagoras Dalam pemecahan masalah
Teks penuh
Gambar


Dokumen terkait
Agar dapat memindahkan energi panas sesuai denga keinginan, maka permukaan perpindahan panas evaporator harus mempunyai kapasitas perpindahan panas yang cukup, agar semua
konsep keilmuan pendukung PJOK secara profesional serta memiliki tanggung jawab personal dan sosial sebagai tauladan bagi peserta didik dan masyarakat sesuai dengan
Dari pernyataan tentang bayi yang menyusu eksklusif jika masih menangis perlu membutuhkan makanan tambahan, dari pernyataan ini diketahui bahwa dari 34 responden didapatkan bahwa
Dengan berlakunya Peraturan Pemerintah ini, maka Tarif atas Jenis Penerimaan Negara Bukan Pajak yang Berlaku pada Departemen Pertanian sebagaimana dimaksud dalam Lampiran IIA
Tenun ikat troso saat ini sedang menjadi primadona dalam bidang industri. Tetapi kalau ditinjau dari perkembangannya jika para pemilik industri-industri kain tenun
10 RESUME HASIL EVALUASI DRT-U / LONG LIST JASA
Berdasarkan Surat Penetapan Pemenang No: 09/POKJA ULP II-PSBN-WG/12/2014 tanggal 19 Desember 2014 bahwa pemilihan Penyedia Barang dan Jasa Paket Pekerjaan
Dalam jangka pendek maupun jangka panjang, permintaan terhadap barang pertanian bersifat tidak elastis, karena jumlah konsumsi hampir sama walaupun harga mahal