PENINGKATAN HASIL BELAJAR OPERASI HITUNG BILANGAN PECAHAN MELALUI PENDEKATAN MATEMATIKA REALISTIK PADA SISWA KELAS V SD NEGERI 3 GRENGGENG.
Teks penuh
Gambar


Garis besar
Dokumen terkait
Tujuan penelitian ini adalah untuk meningkatkan motivasi belajar matematika operasi hitung bilangan melalui model pembelajaran tematik siswa Kelas III Semester I SDN
Berdasarkan latar belakang di atas maka penulis tertarik untuk mengadakan penelitian dengan berkolaborasi bersama guru kelas yang berkaitan dengan pembelajaran matematika
Indikator peningkatan motivasi belajar dapat dilihat dari: (1)Anak mengerjakan tugas benar dari 14 siswa atau 70% meningkat menjadi 17 siswa atau 85%; (2)Siswa kooperatif dengan
Hasil tes siklus II setelah pelaksanaan tindakan, dari 32 siswa kelas IV yang mengikuti pelajaran Matematika dengan penerapan metode evaluasi kecakapan
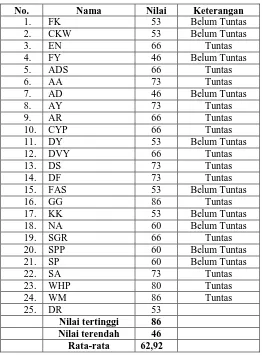
Dari tabel 4.9 dapat diketahui bahwa siswa yang sudah tuntas belajar adalah 22 siswa atau 81,48%, sedangkan siswa yang belum tuntas berjumlah 5 siswa atau 18,52%. Hal ini
7) Hasil tes akhir dan ketuntasan belajar siswa menunjukan lebih dari separoh siswa yang belum tuntas belajarnya. Masih ada beberapa siswa yang masih mendapatkan nilai
Madrasah Ibtidaiyah,” Jurnal Basicedu 6, no.. Dalam PBL, siswa mempunyai tanggung jawab atas pemecahan masalah yang diberikan. Hal ini akan meningkatkan motivasi mereka dalam
Dari hasil diskusi dengan guru kelas, maka diperoleh hal-hal sebagai berikut: 1 Secara umum pelaksanaan pembelajaran telah berjalan sesuai dengan rencana pembelajaran yang disusun