PENENTUAN PUPUK YANG MENGANDUNG NUTRISI SESUAI DENGAN KARAKTER TANAH ENDITIYAS PRATIWI
Teks penuh
Gambar

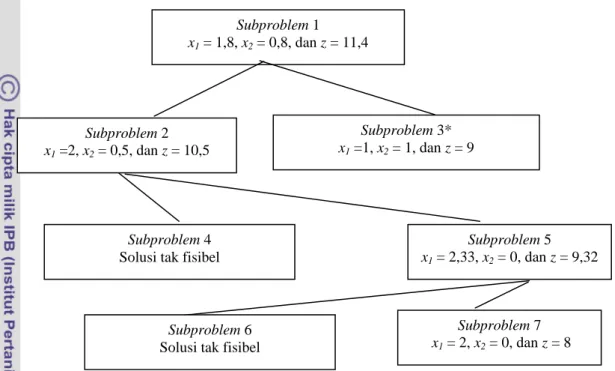
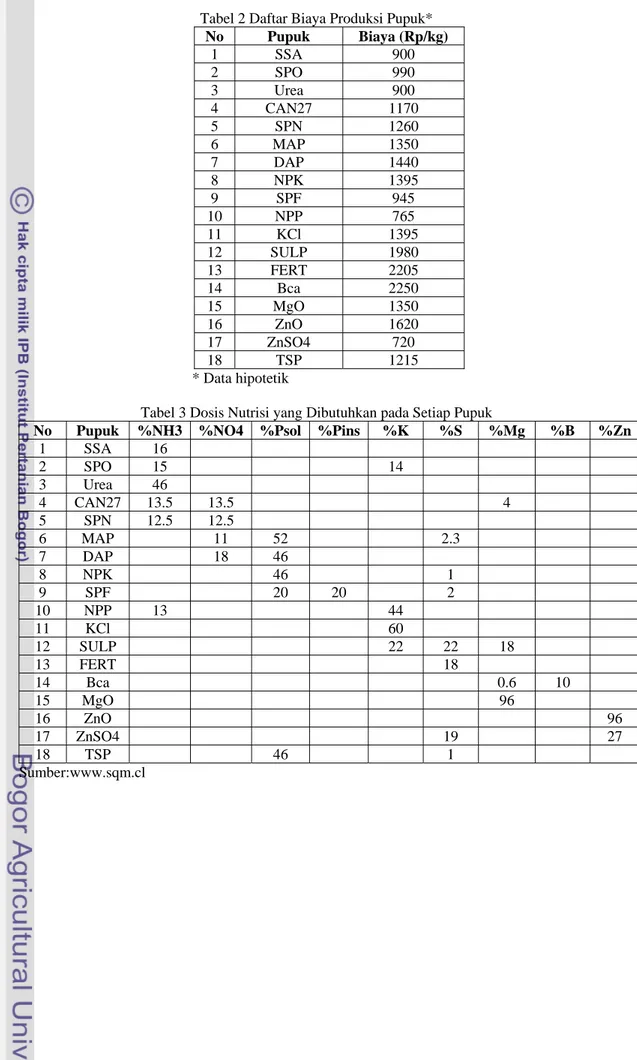
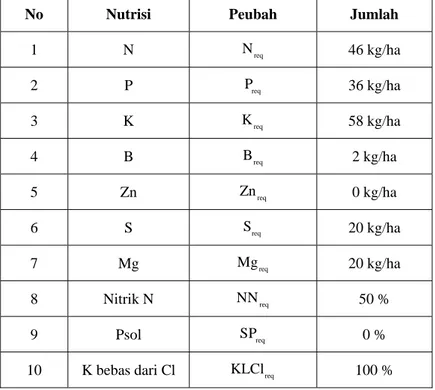
Dokumen terkait
Rendahnya nilai indek keanekaragaman spesies dalam suatu komunitas dapat dipengaruhi oleh beberapa faktor antara lain gangguan lingkungan alami ataupun kegiatan
Dari empat merek, terpilih sembilan varian yang mewakili klaim kandungan gizi yang bervariasi..Tidak jauh berbeda dengan pengambilan sampel MP-ASI bubuk instan,
Pertama, penelitian ini mampu mengidentifikasi karakteristik kualitas website akademik Universitas Telkom menurut karakteristik standar ISO/IEC 9126 yang dapat
mudharabah , diantaranya yaitu pada bagian pengakuan saat penyaluran dana belum diakui sebagai investasi mudharabah , bagian penyajian dana syirkah temporer dan
Setelah kegiatan pembelajaran tentang sistem gerak pada manusia dengan menggunakan model pembelajaran investigasi kelompok dan model pembelajaran observasi dilakukan
Model pembelajaran kooperatif tipe Jigsaw lebih efektif diterapkan dalam pembelajaran daripada model pembelajaran konvensional metode ceramah terhadap hasil belajar matematika siswa
Peneltian ini diperkuat dari hasil penelitian Heldygrad Delvyan jacob, dkk (2012) tentang gambaran pengetahuan dan sikap masyarakat mengenai perilaku pencegahan malaria di