• Tidak ada hasil yang ditemukan

Analisis kemampuan pemecahan masalah matematis siswa dengan pendekatan PMR pada materi Teorema Pythagoras kelas Viii SMP St. Aloysius Turi

N/A
N/A
Info
Unduh - Bebas
Protected

Academic year: 2021

Membagikan "Analisis kemampuan pemecahan masalah matematis siswa dengan pendekatan PMR pada materi Teorema Pythagoras kelas Viii SMP St. Aloysius Turi"

Copied!
334
0
0

Memuat.... (Lihat teks lengkap sekarang)

Unduh sekarang ( 334 Halaman )

Teks penuh

Loading

Gambar

Tabel 3.1. Garis Besar Langkah-langkah Pembelajaran .............................. 37 Tabel 3.2 Kisi-kisi Tes Tertulis .......................................................................
Tabel 3.2. Kisi-Kisi Tes Tertulis Kompetensi Dasar :
Tabel 3.3. Kisi-kisi Lembar Panduan Wawancara Siswa Indikator Kemampuan Pemecahan Masalah Indikator No Butir Pertanyaan Wawancara 1
Tabel 3.4. Teknik Analisis Data Berdasarkan Hubungan Antara Rumusan Masalah dan Metode Pengumpulan Data
+7

Referensi

Unduh sekarang ( PDF - 334 Halaman - 6.16 MB )

Garis besar

Pendidikan Matematika Realistik (PMR) Instrumen Penelitian Pekerjaan siswa kelompok 1 (K1) Masalah 1 Pekerjaan Siswa Kelompok 2 (K2) Masalah 1 Pekerjaan Siswa Kelompok 3 (K3) Masalah 1 Pekerjaan Siswa Kelompok 4 (K4) Masalah 1 Analisis dan Pembahasan Kemampuan Pemecahan Masalah Siswa Kelas VIII C Berdasarkan Hasil Tes dan Wawancara. VIIIC Berdasarkan Hasil Tes dan Wawancara Pekerjaan siswa kelompok 6 (K6) Masalah 1 Pekerjaan siswa kelompok 7 (K7) Masalah 1

Dokumen terkait

EFEKTIVITAS MODEL PEMBELAJARAN DISCOVERY DITINJAU DARI KEMAMPUAN PEMECAHAN MASALAH MATEMATIS DAN SELF CONFIDENCE SISWA (Studi pada Siswa Kelas VIII Semester Ganjil SMP Negeri 8 Bandarlampung Tahun Pelajaran 2015/2016)

Sedangkan kelemahan-kelemahan model pembelajaran discovery yaitu: (1) bagi siswa yang kurang pandai, dapat mengalami kesulitan berpikir dan mengungkapkan hubungan antara

PERBEDAAN KEMAMPUAN PEMECAHAN MASALAH MATEMATIKA SISWA YANG DIAJAR DENGAN MODEL PEMBELAJARAN KOOPERATIF TIPE TPS DAN TIPE STAD PADA MATERI TEOREMA PYTHAGORAS DI KELAS VIII SMPMUHAMMADIYAH PEMATANGSIANTAR.

Berdasarkan uraian yang telah dikemukakan diatas, maka peneliti tertarik untuk mengadakan penelitian dengan judul: “ Perbedaan Kemampuan Pemecahan Masalah Matematika Siswa

KEEFEKTIFAN PENDEKATAN PENDIDIKAN MATEMATIKA REALISTIK DENGAN METODE PEMBELAJARAN PROBLEM SOLVING DITINJAU DARI MOTIVASI BELAJAR DAN KEMAMPUAN PEMECAHAN MASALAH SISWA KELAS VIII SMP N 5 SLEMAN PADA MATERI TEOREMA PYTHAGORAS.

a. Guru membimbing siswa untuk membuat rangkuman isi pembelajaran, pada tahap ini terdapat karakteristik RME yaitu penggunaan hasil konstruksi siswa. Guru

PENGEMBANGAN BAHAN AJAR DENGAN PENDEKATAN KONTEKSTUAL PADA MATERI KUBUS DAN BALOK UNTUK MENINGKATKAN KEMAMPUAN KONEKSI MATEMATIS DAN PEMECAHAN MASALAH SISWA KELAS VIII SMP ISS JATIPURNO WONOGIRI.

Tes kemampuan koneksi matematika digunakan untuk mengukur keefektifan LKS yang dikembangkan ditinjau dari hasil tes kemampuan koneksi matematis. Tes yang diajukan

Efektivitas model pembelajaran think talk write (ttw) dengan pendekatan open ended terhadap kemampuan pemecahan masalah matematis peserta didik pada materi pythagoras kelas VIII di SMP Negeri 1 Adiwerna tahun ajaran 2018/2019

Melalui model pembelajaran think talk write dan pendekatan open ended peserta didik tidak hanya sekedar mendengarkan penjelasan dari guru ataupun mendapatkan contoh

BAB II KAJIAN PUSTAKA - KEMAMPUAN REPRESENTASI MATEMATIS SISWA DALAM MENYELESAIKAN MASALAH TEOREMA PYTHAGORAS DITINJAU DARI PERBEDAAN GENDER KELAS VIII DI SMP NEGERI 1 NGADILUWIH TAHUN AJARAN 2017/2018 - Institutional Repository of IAIN Tulungagung

Berdasarkan uraian di atas dapat disimpulkan bahwa representasi matematis merupakan kemampuan siswa dalam mengungkapkan atau mengkomunikasikan ide/gagasan matematika

BAB II KAJIAN TEORI A. Deskripsi Teoritik - DESKRIPSI KEMAMPUAN PEMECAHAN MASALAH MATEMATIS DAN SIKAP TANGGUNG JAW AB SISWA KELAS VIII SMP NEGERI 1 BUKATEJA PADA MATERI TEOREMA PYTHAGORAS - repository perpustakaan

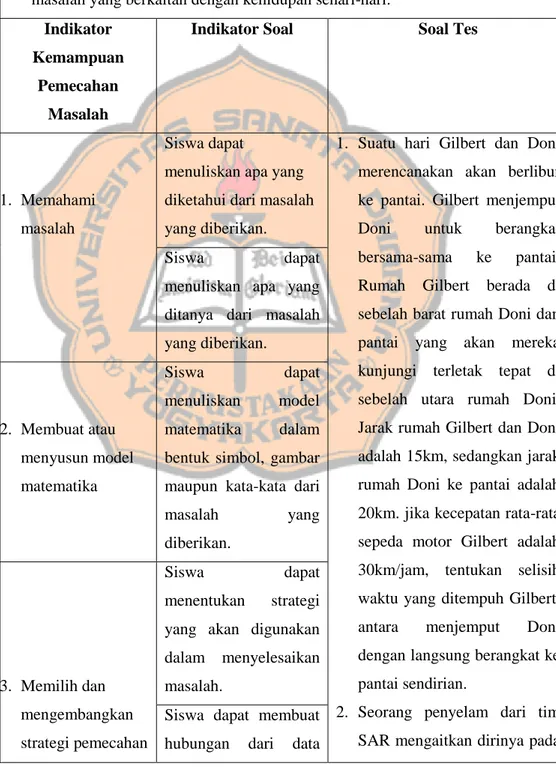
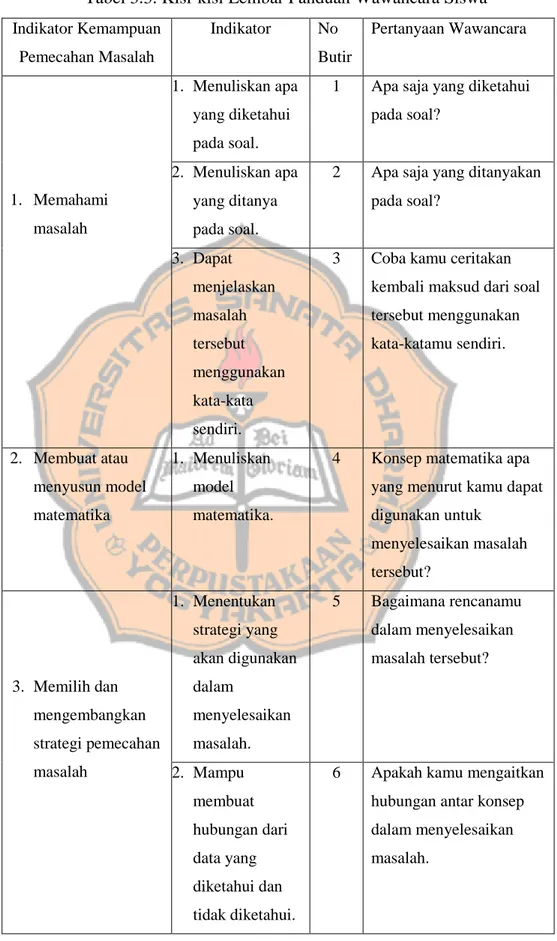
Dalam memahami masalah, dilakukan dengan memunculkan apa yang diketahui, data apa yang diberikan, apa yang tidak.. diketahui (ditanyakan), apakah informasi cukup, syarat

Image