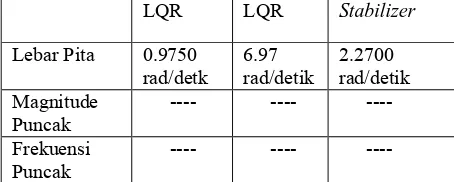
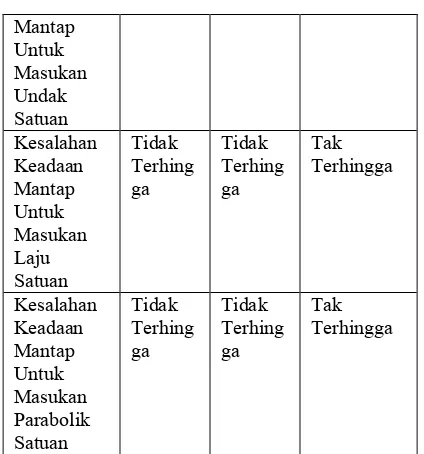
Studi Metoda Kendali Linear Quadratic Regulator (LQR) dan Aplikasinya pada Sistem Automatic Voltage Regulator (AVR).
Teks penuh
Gambar
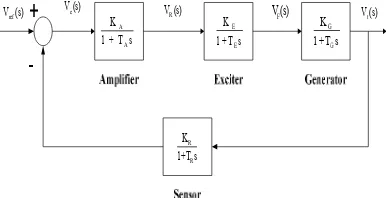
![Gambar 1. Diagram skematik sederhana [12]](https://thumb-ap.123doks.com/thumbv2/123dok/1008800.491868/2.612.108.270.436.536/gambar-diagram-skematik-sederhana.webp)

Dokumen terkait
Karakter mobil VW Beetle yang komunikatif dan atraktif tersebut kemudian ditransformasikan ke dalam elemen-elemen arsitektural yaitu pada fasad bangunan dan tata
Untuk Memenuhi Sebagian Persyaratan Mencapai Derajat Sarjana Ekonomi (S1). Pada Program
konsumen untuk membeli suatu merek atau mengambil tindakan yang. berhubungan dengan pembelian yang diukur dengan
[r]
Tercetus ide dalam benak Rahma untuk membuat makanan “Rujak Buah dengan Bumbu Ulek Gula Jawa Kacang” agar dapat menyegarkan tubuh di saat udara panas. Buah-buahan yang manis
Subjek dari Kajian Lingkungan Hidup Strategis (KLHS) yang dilakukan adalah semua kebijakan, rencana, dan program yang disusun dalam Rencana Pembangunan Jangka
Jenis parkir ini adalah jenis parkir yang tidak terlalu di rekomendasikan, namun tetap memiliki ketentuan khusu bagi tempat- tempat tertentu, misalnya ruko yang
Berikan setiap murid sehelai kertas dan beritahu mereka iaitu aktiviti yang mereka akan buat akan membuktikan sama ada mereka dapat mengikuti arahan yang disampaikan