ANALISIS ASPEK MATEMATIS PADA AKTIVITAS BUDIDAYA JAMUR TIRAM DI DUSUN BERAN
KIDUL, TRIDADI, SLEMAN, YOGYAKARTA DAN IMPLEMENTASINYA DALAM
PEMBELAJARAN MATEMATIKA
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Disusun oleh : Stefani Nita Lystia
NIM : 161414016
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
ANALISIS ASPEK MATEMATIS PADA AKTIVITAS BUDIDAYA JAMUR TIRAM DI DUSUN BERAN
KIDUL, TRIDADI, SLEMAN, YOGYAKARTA DAN IMPLEMENTASINYA DALAM
PEMBELAJARAN MATEMATIKA
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Disusun oleh : Stefani Nita Lystia
NIM : 161414016
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
v
HALAMAN PERSEMBAHAN
Dengan penuh rasa syukur kepada Tuhan Yang Maha Esa, karya ini kupersembahkan kepada :
Allah Bapa dan Bunda Maria yang senantiasa memberkati setiap langkah hidupku.
Ayah, Ibu serta kakakku.
Teman-teman yang telah memberikan dukungan. Almamaterku Universitas Sanata Dharma.
vi
HALAMAN MOTTO
“A dream is your creative vision for your life in the future. A goal is what specifically you intend to make happen. Dreams and goals should be just out of your present reach but not out of sight. Dreams and goals are coming attractions
in your life.”
ix ABSTRAK
Stefani Nita Lystia. 2020. Analisis Aspek Matematis pada Aktivitas Budidaya Jamur Tiram di Dusun Beran Kidul, Tridadi, Sleman, Yogyakarta dan Implementasinya dalam Pembelajaran Matematika. Skripsi. Program Studi Pendidikan Matematika. Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam. Fakultas Keguruan dan Ilmu Pendidikan. Universitas Sanata Dharma.
Tujuan dari penelitian ini untuk mengetahui aspek-aspek matematis yang terdapat pada aktivitas budidaya jamur tiram di Dusun Beran Kidul, Tridadi, Kabupaten Sleman, Yogyakarta dan untuk mengetahui permasalahan kontekstual yang dapat disajikan berdasarkan aktivitas budidaya jamur tiram.
Jenis penelitian ini adalah penelitian deskriptif kualitatif. Objek dalam penelitian ini adalah aspek matematis dan permasalahan kontekstual dari budidaya jamur tiram yang ada di Dusun Beran Kidul, Tridadi, Sleman, Yogyakarta. Metode pengumpulan data yang digunakan adalah observasi, wawancara dan dokumentasi. Teknik analisis data dilakukan dalam 4 tahap yang meliputi reduksi data, kategorisasi, sintesisasi, dan penyusunan hipotesis kerja.
Hasil penelitian menunjukkan bahwa terdapat aspek matematis pada aktivitas budidaya jamur tiram, antara lain : pada proses pembibitan terdapat aktivitas counting dengan aspek matematis berupa perbandingan senilai, pada proses pembuatan media tanam terdapat aktivitas measuring dengan aspek matematis berupa urutan bilangan bulat dan pecahan serta volume bangun ruang, pada proses pemeliharaan terdapat aktivitas measuring dengan aspek matematis berupa operasi hitung bilangan bulat dan pecahan serta aktivitas designing dengan aspek matematis berupa keliling segiempat, pada proses pemanenan terdapat aktivitas measuring dengan aspek matematis berupa statistika dan rasio dua besaran, pada proses produksi hasil olahan terdapat aktivitas measuring dengan aspek matematis berupa persamaan linear dua variabel dan aritmetika sosial, dan pada proses pendistribusian terdapat aktivitas explaining dengan aspek matematis
x
berupa pertidaksamaan linear satu variabel. Aspek matematis yang ditemukan digunakan untuk membuat permasalahan kontekstual matematika tingkat SMP dalam bentuk soal cerita yaitu 7 soal untuk kelas VII, 2 soal untuk kelas VIII, dan 1 soal untuk kelas IX.
Kata kunci : Aktivitas Fundamental Matematis, Aspek Matematis, Budidaya Jamur Tiram.
xi ABSTRACT
Stefani Nita Lystia. 2020. Mathematics Aspect Analysis in Activity of Oysters Mushroom Cultivation in Beran Kidul, Tridadi, Sleman, Yogyakarta and Its Implementation in Mathematics Learning. Undergraduate Thesis. Mathematics Education Study Program. Department of Mathematics and Science Education. Faculty of Teacher Training and Education. Sanata Dharma University.
This study aims to find out mathematics aspects in activity of oysters mushroom cultivation in Beran Kidul, Tridadi, Sleman, Yogyakarta and to find out contextual problem that can be made from the activity of oysters mushroom cultivation.
This study was a descriptive qualitative. The object of this study was mathematics aspect and contextual problem in activity of oysters mushroom cultivation in Beran Kidul, Tridadi, Sleman, Yogyakarta. The data collection methods were observations, interviews, and documentation. Technic of Data Analysis consist of 4 step, there were data reduction, categorization, synthesis, and arrange the working hypothesis.
The results of this study showed there were mathematics aspects in activity of oysters mushroom cultivation, include : in inoculating process there is counting activity with direct proportion as a mathematics aspect, in making growing media process there is measuring activity with sequence of integers and rational number and volume of solid as a mathematics aspect, in maintenance process there is measuring activity with integers and rational number operations as a mathematics aspect and designing activity with circumference of quadrilaterals as a mathematics aspect, in harvesting process there is measuring activity with statistics and ratio of two quantities as a mathematics aspect, in production process there is measuring activity with linear equation of two variables and social arithmetic as a mathematics aspect, in distribution process there is explaining activity with linear inequality of one variable as a mathematics aspect. Mathematics aspects that found used to make mathematics contextual problem
xii
for junior high school in story problem consist of 7 questions for VII grade, 2 questions for VIII grade, and 1 question for IX grade.
Keywords : Fundamental Mathematics Activity, Mathematics Aspect, Oysters Mushroom Cultivation.
xv DAFTAR ISI
HALAMAN SAMPUL ... i
HALAMAN JUDUL ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
HALAMAN MOTTO ... vi
PERNYATAAN KEASLIAN KARYA ... vii
LEMBAR PERNYATAAN PERSETUJUAN ... viii
ABSTRAK ... ix
ABSTRACT ... xi
KATA PENGANTAR ... xiii
DAFTAR ISI ... xv
DAFTAR TABEL ... xvii
DAFTAR GAMBAR ... xviii
DAFTAR LAMPIRAN ... xix
BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Identifikasi Masalah ... 2 C. Rumusan Masalah ... 3 D. Tujuan Penelitian ... 3 E. Pembatasan Masalah ... 3 F. Penjelasan Istilah ... 4 G. Manfaat Penelitian ... 4 H. Sistematika Penulisan ... 5
BAB II LANDASAN TEORI ... 6
A. Tinjauan Pustaka ... 6
B. Penelitian yang Relevan ... 40
C. Kerangka Berpikir ... 41
xvi
A. Jenis Penelitian ... 44
B. Narasumber Penelitian ... 44
C. Objek Penelitian ... 44
D. Tempat dan Waktu Penelitian ... 44
E. Bentuk Data ... 45
F. Metode Pengumpulan Data ... 45
G. Instrumen Pengumpulan Data ... 46
H. Teknik Analisis Data ... 47
I. Prosedur Pelaksanaan Penelitian ... 48
BAB IV HASIL DAN PEMBAHASAN ... 50
A. Pelaksanaan Penelitian ... 50 B. Penyajian Data ... 51 C. Analisis Data ... 66 D. Pembahasan ... 77 E. Keterbatasan Penelitian ... 93 BAB V PENUTUP ... 94 A. Kesimpulan ... 94 B. Saran ... 95 DAFTAR PUSTAKA ... 96 LAMPIRAN ... 98
xvii
DAFTAR TABEL
Tabel 2.1. Aspek Matematis... 11
Tabel 4.1. Data Aktivitas Counting pada Proses Budidaya Jamur Tiram ... 51
Tabel 4.2. Data Aktivitas Measuring pada Proses Budidaya Jamur Tiram ... 53
Tabel 4.3. Data Aktivitas Designing pada Proses Budidaya Jamur Tiram ... 60
Tabel 4.4. Data Aktivitas Explaining pada Proses Budidaya Jamur Tiram ... 62
Tabel 4.5. Hasil Terkait Aktivitas Fundamental Matematis pada Budidaya Jamur Tiram ... 66
Tabel 4.6. Kategori-kategori Terkait Aktivitas Fundamental Matematis pada Budidaya Jamur Tiram ... 74
Tabel 4.7. Hasil Sintesisasi Data ... 76
Tabel 4.8. Aspek Matematis pada Budidaya Jamur Tiram ... 77
xviii
DAFTAR GAMBAR
Gambar 2.1. Garis Bilangan ... 11
Gambar 2.2. Perkalian Bilangan Bulat ... 12
Gambar 2.3. Diagram Lingkaran Acara Televisi...25
Gambar 2.4. Persegi Panjang ... 29
Gambar 2.5. Garis Singgung Persekutuan Luar 2 Lingkaran ... 31
Gambar 2.6. Garis Singgung Persekutuan Dalam 2 Lingkaran ... 31
Gambar 2.7. Refleksi... 37
Gambar 2.8. Translasi ... 37
Gambar 2.9. Rotasi ... 38
Gambar 2.10. Dilatasi ... 38
Gambar 2.11. Dua Bangun Kongruen ... 39
Gambar 2.12. Dua Bangun Sebangun ... 39
Gambar 2.13. Bagan Kerangka Berpikir ... 43
Gambar 4.1. Bahan untuk Pembuatan Media Tanam ... 67
Gambar 4.2. Botol Kaca ... 70
Gambar 4.3. Autoklaf ... 70
Gambar 4.4. Tabung Boiler ... 71
Gambar 4.5. Media Tanam Baglog ... 71
Gambar 4.6. Kumbung ... 72
Gambar 4.7. Bakso Jamur Tiram ... 72
xix
DAFTAR LAMPIRAN
Lampiran 1 : Surat Ijin Penelitian ... 99
Lampiran 2 : Surat Keterangan Telah Melakukan Penelitian ... 100
Lampiran 3 : Kisi-kisi Pedoman Wawancara... 101
Lampiran 4 : Pedoman Wawancara ... 105
Lampiran 5 : Lembar Validasi Pedoman Wawancara... 107
Lampiran 6 : Kisi-kisi Pedoman Observasi ... 110
Lampiran 7 : Pedoman Observasi ... 112
Lampiran 8 : Lembar Validasi Pedoman Observasi ... 114
Lampiran 9 : Transkrip Data Narasumber ... 117
1 BAB I PENDAHULUAN
A. Latar Belakang
Sejak awal peradaban manusia, matematika telah berperan dalam setiap kegiatan pada kehidupan manusia. Kata "matematika" berasal dari bahasa Yunani Kuno máthēma, yang berarti pengkajian, pembelajaran, ilmu yang ruang lingkupnya menyempit, dan arti teknisnya menjadi "pengkajian matematika". Matematikawan asal Jerman yaitu Carl Friedrich Gauss mengatakan “Mathematics is the Queen of Science” yang dapat diartikan sebagai matematika adalah ratu dari ilmu pengetahuan. Hal itu berarti bahwa, matematika adalah dasar bagi perkembangan ilmu pengetahuan yang lain. Itulah kenapa, belajar matematika itu penting karena matematika memiliki banyak peranan dalam setiap aspek kehidupan.
Di Indonesia, matematika merupakan mata pelajaran yang dipelajari oleh semua jenjang pendidikan. Namun hingga saat ini, masih banyak peserta didik yang merasa bahwa matematika itu sulit bahkan masih ada beberapa peserta didik yang menganggap bahwa matematika kurang implementatif. Penyebab peserta didik merasa matematika itu sulit dan kurang implementatif adalah karena soal-soal atau permasalahan yang diberikan kurang kontekstual. Kontekstual yang dimaksud adalah permasalahan yang disajikan kurang dikaitkan dengan situasi di kehidupan nyata siswa. Hal tersebut peneliti peroleh ketika berinteraksi secara langsung dengan peserta didik, pada saat peneliti sedang menjalani program Pengenalan Lapangan Persekolahan (PLP).
Perlu adanya perbaikan dalam proses pembelajaran matematika agar tercipta suatu pembelajaran yang bermakna bagi peserta didik. Alasan perlu adanya perbaikan adalah untuk mengubah pola pikir siswa yang mengatakan bahwa matematika kurang implementatif. Mengingat bahwa matematika memiliki banyak peranan dalam setiap aspek kehidupan, maka guru dapat mengenalkan matematika melalui permasalahan-permasalahan kontekstual
yang ada dalam kehidupan nyata. Dari hal tersebut, maka peneliti merasa perlu untuk mengkaji matematika pada salah satu jenis usaha yang sedang berkembang pesat yaitu budidaya jamur tiram, di mana jamur tiram sendiri sudah dikenal oleh masyarakat luas. Alasan peneliti merasa perlu untuk mengkaji matematika pada budidaya jamur tiram adalah karena ternyata di setiap proses budidaya jamur tiram terdapat aspek matematis yang dapat di implementasikan dalam pembelajaran matematika tingkat SMP. Peneliti memilih budidaya jamur tiram karena budidaya jamur tiram adalah salah satu jenis usaha yang mudah ditemukan hampir di seluruh daerah di Indonesia dan jamur tiram sendiri sudah umum bagi masyarakat Indonesia.
Jamur tiram adalah salah satu jenis jamur konsumsi yang kini semakin populer di Indonesia. Pasalnya, sudah banyak petani yang membudidayakan jamur yang mirip seperti payung ini. Di antara berbagai jenis jamur tiram, yang paling dikenal adalah jamur tiram putih. Salah satu tokoh yang membuka usaha budidaya jamur tiram adalah Pak Bagus. Usaha budidaya jamur tiram milik Pak Bagus telah berlangsung sejak tahun 2010. Awalnya, petani yang bekerjasama dengan Pak Bagus hanya segelintir orang. Namun, karena hasilnya menjanjikan maka, semakin banyak petani yang ingin membudidayakan jamur tiram. Hasil olahan jamur tiram juga sudah banyak kita jumpai di berbagai rumah makan. Aktivitas budidaya jamur tiram di dusun Beran Kidul, Tridadi, Sleman, Yogyakarta ini meliputi berbagai proses seperti pembibitan, perawatan, pemanenan, hingga penjualan.
Berdasarkan hal tersebut, peneliti akan mengkaji lebih dalam lagi mengenai aspek-aspek matematis yang terdapat pada aktivitas budidaya jamur tiram dengan berdasarkan pada enam aktivitas fundamental matematis menurut Bishop.
B. Identifikasi Masalah
Berdasarkan latar belakang di atas, maka peneliti mengindentifikasi masalah sebagai berikut :
1. Bagi beberapa peserta didik, matematika dirasakan sebagai mata pelajaran yang sulit dan kurang implementatif.
2. Soal atau permasalahan yang diberikan guru kurang kontekstual yang mengakibatkan siswa kurang bisa melihat hubungan matematika dengan hidup mereka sehari-hari.
C. Rumusan Masalah
Berdasarkan latar belakang yang telah dipaparkan, maka diperoleh rumusan masalah sebagai berikut :
1. Apa saja aspek-aspek matematis yang terdapat pada aktivitas budidaya jamur tiram di Dusun Beran Kidul, Tridadi, Kabupaten Sleman?
2. Bagaimana permasalahan kontekstual yang dapat disajikan dari budidaya jamur tiram?
D. Tujuan Penelitian
Berdasarkan rumusan masalah di atas, maka tujuan dari penelitian ini adalah untuk :
1. Mengetahui apa saja aspek-aspek matematis yang terdapat pada aktivitas budidaya jamur tiram di Dusun Beran Kidul, Tridadi, Kabupaten Sleman. 2. Mengetahui permasalahan kontekstual yang dapat disajikan dari budidaya
jamur tiram.
E. Pembatasan Masalah
1. Masalah penelitian ini dibatasi pada pendeskripsian aktivitas budidaya jamur tiram menurut tokoh yang memiliki bidang usaha budidaya jamur tiram di Dusun Beran Kidul, Tridadi, Sleman.
2. Penentuan aspek matematis ditentukan melalui enam aktivitas fundamental matematis menurut Bishop (1988) pada setiap aktivitas budidaya jamur tiram yang dilakukan oleh tokoh.
F. Penjelasan Istilah 1. Aspek Matematis
Aspek matematis berarti sudut pandang yang bersifat matematika. Aspek matematis dalam penelitian ini merupakan materi-materi matematika untuk tingkat SMP.
2. Budidaya Jamur Tiram
Budidaya jamur tiram merupakan kegiatan mengembangkan dan menghasilkan bahan pangan berupa jamur tiram.
G. Manfaat Penelitian
Manfaat penelitian ini adalah sebagai berikut : 1. Manfaat Teoritis
a. Sebagai sumbangsih ilmu dalam Ilmu Pendidikan, yaitu membuat inovasi dalam pembelajaran matematika khususnya dalam pembuatan permasalahan konteksual.
b. Sebagai referensi pada penelitian-penelitian selanjutnya. 2. Manfaat Praktis
a. Bagi Guru
Penelitian ini diharapkan dapat menjadi inovasi dalam pembelajaran khususnya dalam membuat permasalahan kontekstual.
b. Bagi Peneliti
Dapat menambah wawasan dan pengalaman langsung tentang proses budidaya jamur tiram.
c. Bagi Peneliti Lain
Penelitian ini diharapkan dapat menjadi referensi bagi peneliti yang lain.
H. Sistematika Penulisan
Skripsi ini terdiri dari lima bab. Berikut adalah uraian untuk setiap bab. 1. Bab I adalah pendahuluan yang mendiskusikan latar belakang, identifikasi
masalah, rumusan masalah, tujuan penelitian, pembatasan masalah, penjelasan istilah, manfaat penelitian, dan sistematika penulisan.
2. Bab II merupakan landasan teori yang berisi pembahasan berkaitan dengan konsep-konsep yang mendasari skripsi, yaitu budidaya jamur tiram, aktivitas fundamental matematis, aspek matematis, penelitian yang relevan, dan kerangka berpikir.
3. Bab III mendiskusikan metode penelitian. Pada bab ini dipaparkan jenis penelitian, narasumber penelitian, objek penelitian, tempat dan waktu penelitian, bentuk data, metode pengumpulan data, instrumen pengumpulan data, teknik analisis data, dan prosedur pelaksanaan penelitian.
4. Bab IV memaparkan hasil dan pembahasan penelitian. Bab ini mendiskusikan pelaksanaan penelitian, penyajian data, analisis data, pembahasan, dan keterbatasan penelitian.
6 BAB II LANDASAN TEORI
A. Tinjauan Pustaka
1. Budidaya Jamur Tiram
Budidaya dapat diartikan sebagai berbagai jenis kegiatan untuk mengembangkan dan memanfaatkan sumber daya alam nabati yang dikerjakan manusia dengan menggunakan modal, teknologi dan sumber daya lainnya untuk menghasilkan suatu produk berupa barang untuk memenuhi kebutuhan manusia (PP Republik Indonesia No. 18 Tahun 2010). Sedangkan budidaya tanaman dapat diartikan sebagai proses untuk menghasilkan bahan pangan serta berbagai produk agroindustri lainnya dengan memanfaatkan sumber daya tumbuhan (Hanum, 2008). Berdasarkan hal tersebut, maka dapat dikatakan bahwa budidaya jamur tiram merupakan kegiatan mengembangkan dan menghasilkan bahan pangan berupa jamur tiram. Chairani Hanum (2008:2) mengatakan bahwa ada 3 hal pokok yang membuat suatu kegiatan dapat dikatakan sebagai tindakan budidaya, yaitu : (1) melakukan pengolahan tanah, (2) pemeliharaan untuk mencapai produksi maksimum, (3) tindak berpindah-pindah lokasi.
Menurut Badan Pusat Statistik tahun 2017, tingkat konsumsi jamur di Indonesia mencapai 47.753 ton sedangkan produksinya hanya 37.020 ton. Dari beberapa jenis jamur konsumsi, yang paling banyak diminati adalah jamur tiram. Jamur tiram (Pleurotus Ostreatus) tergolong dalam jamur edible (dapat dikonsumsi) yang diketahui sangat enak rasanya dan memiliki kandungan gizi yang tinggi antara lain protein, asam lemak tidak jenuh vitamin dan mineral yang sangat berguna bagi kesehatan (Umniyatie, Astuti, Pramiadi, Henuhili, 2013). Nurheti Yuliarti (2017:5) mengatakan bahwa protein yang terkandung dalam jamur tiram dua kali lipat lebih tinggi dibanding asparagus dan kubis. Tak hanya itu, jamur tiram juga mengandung 9 asam amino esensial dan merupakan sumber
mineral yang baik.
Jamur tiram merupakan jenis jamur yang paling sering dibudidayakan karena memiliki berbagai keunggulan, seperti : (1) harga yang relatif stabil sehingga tingkat keuntungan yang dihasilkan relatif tinggi, (2) umur singkat, dan (3) permintaan pasar yang tinggi (Yuliarti, 2017). Menurut Purbo yang dikutip oleh Umniyatie, Astuti, Pramiadi, Henuhili (2013), ada beberapa langkah dalam budidaya jamur tiram, yaitu :
a. Penyiapan Bibit Jamur
Bibit jamur yang disiapkan adalah bibit F1, F2, dan F3. F (Filial) memiliki arti turunan ke-1, 2, dan 3. Bibit F1 adalah bibit induk dari turunan pertama yang sangat mempengaruhi kualitas bibit pada turunan berikutnya. Untuk membuat bibit F1 diperlukan teknik yang rumit yang biasa disebut teknik aseptik.
b. Penyiapan Rumah Jamur
Pemilihan rumah jamur diupayakan yang memiliki suhu 30-32 C dan dekat dengan sumber air. Rumah jamur harus beratap genting, dan dindingnya terbuat dari anyaman bambu yang dilapisi plastik. Rumah jamur harus dilengkapi dengan pintu dan jendela untuk mengatur sirkulasi udara.
c. Pembuatan Media Tanam Jamur
Media tanam jamur berbahan dasar serbuk gergaji yang sudah diayak, gips (CaSO4), kapur (CaCO3), bekatul, TSP dan air.
d. Sterilisasi Media Tanam
Sterilisasi dilakukan untuk menghindari adanya kontaminasi organisme lain yang dapat mengganggu pertumbuhan jamur. Sterilisasi dilakukan dengan menggunakan tabung boiler dengan suhu 120 C dan tekanan 1 atmosfer selama 5-6 jam.
e. Inokulasi Bibit
Inokulasi bibit adalah langkah mengisikan bibit jamur ke dalam media tanam baglog yang sudah dingin. Bibit yang digunakan adalah bibit F3
yang diisikan dengan teknik aseptik (dilakukan di dekat lampu bunsen/lampu spiritus) dengan menggunakan pinset yang steril.
f. Inkubasi
Inkubasi media tanam yang sudah diberi bibit, dilakukan pada ruang inkubasi yang memiliki suhu ruangan antara 22-28 C. Proses ini dilakukan untuk menumbuhkan miselium dan biasanya memakan waktu hingga 30 hari atau lebih.
g. Pembukaan Tutup Kapas
Jika miselium sudah memenuhi baglog, kapas yang menjadi tutup baglog dapat dibuka. 1-7 hari setelah proses ini, calon jamur akan tumbuh.
h. Pemeliharaan
Untuk mencegah timbulnya hama dan penyakit, biasanya dilakukan dengan cara menaburkan kapur pada celah-celah susunan baglog, dan membuang baglog yang terkontaminasi.
i. Pemanenan
Pemanenan dapat dilakukan 1-2 minggu setelah tutup kapas dibuka. Pemanenan sebaiknya dilakukan pada pagi hari dengan cara mencabut seluruh rumpun jamur, kemudian dibersihkan.
2. Aktivitas Fundamental Matematis
Menurut Bishop (1988:99) terdapat enam aktivitas dasar matematika yang terdiri dari counting (membilang), locating (menentukan lokasi),
measuring (mengukur), designing (merancang), playing (bermain), dan explaining (menjelaskan). Penjelasan terkait enam aktivitas fundamental
matematis menurut Bishop adalah sebagai berikut. a. Counting
Counting (membilang) merupakan suatu aktivitas yang meliputi
kuantifikasi atau pernyataan yang menyatakan jumlah seperti penggunaan kuantor universal (menggunakan kata : setiap, seluruh) dan kuantor eksistensial (menggunakan kata : ada, beberapa, terdapat)
dalam logika matematika, nama-nama bilangan, penggunaan jari dan bagian tubuh untuk menghitung, turus, bilangan, nilai tempat, nol, basis 10, operasi bilangan, kombinatorik, akurasi, perkiraan, kesalahan dalam membilang, pecahan, desimal, positif, negatif, besar tidak terhingga, kecil tidak terhingga, limit, pola bilangan, pangkat, relasi bilangan, diagram panah, representasi aljabar, kejadian, probabilitas, representasi frekuensi. Pada awalnya, aktivitas counting (membilang) muncul dalam masyarakat karena kebutuhan masyarakat untuk membuat catatan berdasarkan harta kepemilikan mereka seperti perhitungan untuk menghitung jumlah hewan ternak yang mereka miliki.
b. Locating
Locating (menentukan lokasi) merupakan suatu aktivitas yang
meliputi preposisi, pendeskripsian suatu rute/lintasan, lokasi lingkungan, arah mata angin, atas/bawah, depan/belakang, jarak, garis lurus/garis lengkung, sudut sebagai penanda perputaran, sistem lokasi, koordinat kutub yaitu pasangan (r, ) dari titik P dimana r adalah jari-jari lingkaran dan adalah salah satu sudut antara sinar dan sumbu kutub, koordinat kartesius, pemetaan, lintang/bujur, tempat kedudukan, penghubungan, lingkaran. Awalnya, aktivitas locating (menentukan lokasi) digunakan manusia untuk menentukan dimana tempat yang cocok untuk berburu.
c. Measuring
Measuring (mengukur) merupakan suatu aktivitas seperti pembanding
kuantitas, mengurutkan, kualitas, pengembangan dari satuan, keakuratan satuan, perkiraan, panjang, luas, volume, waktu, suhu, berat, satuan konvensional yaitu satuan berdasarkan kesepakatan umum (Contoh : satuan berat yaitu kg, hg, dag, g, dg, cg, mg dan satuan panjang yaitu km, hm dam, m, dm, cm, mm), satuan standar, sistem satuan, uang, satuan majemuk yaitu satuan yang terdiri dari beberapa bagian yang merupakan kesatuan (Contoh : km/jam,
km/menit, m/menit, m/detik). Awalnya, aktivitas ini digunakan untuk membandingkan antara dua objek kemudian berkembang menjadi banyak objek.
d. Designing
Designing (merancang) merupakan aktivitas yang meliputi rancangan,
abstraksi, bentuk geometris, estetika, membandingkan objek dengan sifat bentuk, besar, kecil, kesebangunan, kekongruenan, sifat-sifat bangun, bentuk geometris umum, benda padat, jaringan, permukaan, pengubinan, simetri, proporsi, perbandingan, pembesaran skala, kelakuan suatu benda. Aktivitas ini dapat kita jumpai dalam kehidupan sehari-hari seperti bentuk bangunan, bentuk kerajinan tangan, dan sebagainya.
e. Playing
Playing (bermain) merupakan aktivitas yang meliputi pertandingan,
teka-teki, paradoks, pemodelan, aktivitas terikat aturan, penalaran hipotesis yaitu cara berpikir logis untuk membuat anggapan dasar, prosedur, strategi rencana, permainan kerjasama, permainan kompetitif, permainan solitaire, kemungkinan, prediksi. Aktivitas ini dapat kita jumpai dalam berbagai macam permainan yang berkembang di masyarakat. Melalui permainan, dapat ditemukan aspek-aspek matematis seperti membuat strategi agar menang dalam pertandingan, memprediksi kemungkinan yang terjadi, dan sebagainya.
f. Explaining
Explaining (menjelaskan) merupakan aktivitas yang meliputi
kesamaan dalam bentuk benda-benda, klasifikasi, penjelasan cerita, logika koneksi, penjelasan, argumen logis, pembuktian, penjelasan dengan simbol-simbol, diagram, grafik, matriks, pemodelan matematika, kriteria, validitas internal, generalisabilitas eksternal.
3. Aspek Matematis
Kamus Besar Bahasa Indonesia (KBBI) mengartikan aspek sebagai sudut pandang, sedangkan matematis memiliki arti bersifat matematika. Dari arti tersebut, dapat ditarik kesimpulan bahwa aspek matematis merupakan sudut pandang yang bersifat matematika. Berikut ini adalah aspek matematis berdasarkan Kompetensi Dasar (Kemendikbud, 2017) mata pelajaran matematika untuk tingkat SMP.
Tabel 2.1. Aspek Matematis
No. Kelas Aspek Matematis Kompetensi Dasar 1. VII Urutan bilangan
bulat dan pecahan
4.1. Menyelesaikan masalah yang berkaitan dengan urutan beberapa bilangan bulat dan pecahan (biasa, campuran, desimal, persen).
Sekilas Materi :
Gambar 2.1. Garis Bilangan Sumber : Kemendikbud
Bilangan yang lebih besar selalu berada di kanan bilangan yang lebih kecil. Begitupula dengan bilangan pecahan. Namun, jika yang dibandingkan adalah bilangan bulat positif yang sangat besar atau bilangan bulat negatif yang sangat kecil maka yang dilihat adalah angka-angka penyusunnya. Begitupula dengan bilangan pecahan.
Contoh :
Urutkan bilangan bulat berikut dari yang terkecil ke terbesar :
5, -3, -8, 10
Maka urutannya adalah -8,-3,5,10.
Urutkan bilangan pecahan berikut dari yang terbesar ke yang terkecil :
Maka urutannya adalah
2. VII Operasi hitung bilangan bulat dan pecahan
4.2. Menyelesaikan masalah yang berkaitan dengan operasi hitung bilangan bulat dan pecahan.
Sekilas Materi :
Penjumlahan Bilangan Bulat Sifat Komutatif
a + b = b + a Sifat Asosiatif
a + (b + c) = (a + b) + c Pengurangan Bilangan Bulat Perkalian Bilangan Bulat
Gambar 2.2. Perkalian Bilangan Bulat
Sumber : Kemendikbud Sifat Komutatif
a × b = b × a Sifat Asosiatif a × (b × c) = (a × b) × c Sifat Distributif Terhadap penjumlahan a × (b + c) = (a × b) + (a × c) Terhadap pengurangan a × (b - c) = (a × b) - (a × c) Pembagian Bilangan Bulat
Untuk a, b, c bilangan bulat Jika a × b = c maka dengan b 0 Jika a × b = c maka dengan a 0 Contoh : (- 4) + 2 = 2 + (-4) = - 2 1 × (3 - 5) = (1 × 3) - (1 × 5) = - 2 3. VII Bilangan berpangkat
4.3. Menyelesaikan masalah yang berkaitan dengan bilangan dalam bentuk bilangan berpangkat bulat positif dan negatif.
Sekilas Materi :
Bilangan berpangkat adalah bilangan yang dinyatakan dalam bentuk dengan a dan b adalah bilangan bulat. Dalam hal ini, a disebut dengan bilangan
basis/pokok dan b disebut eksponen/pangkat.
Contoh :
4. VII Himpunan 4.4. Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta,
himpunan kosong,
komplemen himpunan, dan operasi biner pada himpunan. Sekilas Materi :
Himpunan A merupakan himpunan bagian B jika setiap anggota A juga menjadi anggota B dan dinotasikan dengan . Contoh :
Maka .
Himpunan semesta adalah himpunan seluruh unsur yang menjadi objek pembicaraan, dan dilambangkan dengan S.
Contoh :
Tentukan himpunan semesta yang mungkin dari himpunan B =
Maka himpunan semesta yang mungkin dari himpunan B adalah
S =
S =
S =
Himpunan kosong adalah himpunan yang tidak memiliki anggota yang dinotasikan dengan atau .
Contoh :
C adalah himpunan nama-nama hari yang diawali dengan huruf y. Maka : C =
Karna n(C) = 0
Komplemen himpunan A adalah suatu himpunan yang semua anggotanya ada di himpunan S tetapi bukan anggota himpunan A, dinotasikan dengan . Komplemen himpunan dinotasikan : Contoh : S = A = Maka =
Operasi biner dalam himpunan : Irisan
Irisan dari himpunan A dan B adalah himpunan yang anggotanya semua anggota S
yang merupakan anggota himpunan A dan anggota himpunan B, dilambangkan dengan . Irisan dua himpunan dinotasikan :
. Gabungan
Gabungan dari himpunan A dan B adalah himpunan yang anggotanya semua anggota S yang merupakan anggota himpunan A atau anggota himpunan B, dilambangkan dengan . Gabungan dua himpunan dinotasikan :
Selisih
Selisih himpunan B terhadap himpunan A adalah himpunan semua anggota himpunan A yang bukan anggota himpunan B, dinotasikan dengan A – B. Selisih dua himpunan dinotasikan : . 5. VII Bentuk aljabar 4.5. Menyelesaikan masalah yang berkaitan dengan bentuk aljabar dan operasi pada bentuk aljabar.
Sekilas Materi :
matematis atau model matematika. Nama-nama bentuk aljabar berdasarkan banyaknya suku :
2, x, dan 2x disebut monomial
2x + 4 disebut binomial
2x + 3y + 7 disebut trinomial Pada bentuk 2x + 4, bilangan 2 disebut koefisien, x disebut variabel, 4 disebut konstanta. Contoh :
2 kotak bola dan 4 bola Misalkan
Banyak bola dalam 1 kotak = a Bentuk aljabarnya adalah 2a + 4
6. VII Persamaan dan pertidaksamaan linear satu variabel
4.6. Menyelesaikan masalah yang berkaitan dengan persamaan dan pertidaksamaan linear satu variabel.
Sekilas Materi :
Persamaan linear satu variabel adalah kalimat terbuka yang dihubungkan tanda sama dengan (=) dan hanya mempunyai satu variabel berpangkat 1. Bentuk umum persamaan linear satu variabel adalah ax + b = 0.
Contoh : x + 3 = 7 13 = p – 4
Pertidaksamaan linear satu variabel adalah kalimat terbuka yang dinyatakan dengan
menggunakan tanda
ketidaksamaan (<, >, ) dan hanya mempunyai satu variabel berpangkat 1.
Contoh : m + 5 7 13 x + 14
7. VII Rasio dua besaran 4.7. Menyelesaikan masalah yang berkaitan dengan rasio dua besaran (satuannya sama dan berbeda).
Sekilas Materi :
Perbandingan atau rasio digunakan untuk membandingkan besaran suatu benda dengan benda lainnya. Besaran benda yang dimaksud dapat berupa panjang, kecepatan, massa, waktu, dan sebagainya. Contoh :
Fany dan Aryo adalah teman sekelas. Rumah Fany berjarak 500 meter dari sekolah. Rumah Aryo berjarak 2 km dari sekolah. Berapakah perbandingan jarak rumah Fany dan Aryo dari sekolah?
Perbandingan jarak rumah Fany terhadap jarak rumah Aryo adalah 500 : 2.000 = 1 : 4
Maka perbandingan jarak rumah Fany terhadap jarak rumah Aryo adalah 1 : 4 atau jarak rumah Fany dari sekolah adalah 4 kali jarak rumah Aryo dari sekolah.
8. VII Perbandingan senilai dan berbalik nilai
4.8. Menyelesaikan masalah yang
berkaitan dengan
perbandingan senilai dan berbalik nilai.
Sekilas Materi :
Perbandingan senilai adalah perbandingan antara dua besaran yang apabila salah satu besaran nilainya semakin besar maka nilai besaran yang lain akan semakin besar pula.
Contoh :
Sebuah mesin di suatu pabrik minuman mampu memasang tutup botol untuk 14 botol dalam waktu 84 detik. Banyak botol yang dapat ditutup oleh mesin dalam waktu 2 menit adalah ...
Jawaban : Misalkan :
Perbandingan banyaknya botol yang dapat ditutup terhadap waktu adalah
14 : 84 = 1 : 6
Banyaknya botol yang dapat ditutup dalam waktu 2 menit adalah
Maka banyaknya botol yang dapat ditutup dalam waktu 2 menit adalah 20 botol.
Perbandingan berbalik nilai adalah perbandingan dua besaran yang bila salah satu besaran nilainya semakin besar maka nilai besaran yang lain akan semakin kecil.
Contoh :
Suatu pekerjaan dapat diselesaikan selama 16 hari oleh 8 orang pekerja. Jika 4 pekerja ditugaskan ke pekerjaan lain, lama waktu yang bisa diselesaikan oleh pekerja yang tersisa adalah ...
Misalkan : x = waktu yang diperlukan
Perbandingan jumlah pekerja terhadap waktu adalah
8 : 16
Lama waktu yang dibutuhkan saat dikerjakan oleh 4 pekerja adalah
32
Maka lama waktu yang dibutuhkan saat dikerjakan oleh 4 pekerja adalah 32 hari.
9. VII Aritmetika sosial 4.9. Menyelesaikan masalah yang berkaitan dengan aritmetika sosial (penjualan, pembelian, potongan, keuntungan, kerugian, bunga tunggal, persentase, bruto, neto, tara). Sekilas Materi :
Aritmetika sosial biasa digunakan untuk membahas kegiatan terkait dunia perekonomian seperti penjualan, pembelian, potongan, keuntungan, kerugian, bunga tunggal, persentase, bruto, neto, tara.
Seorang penjual krupuk mengeluarkan modal sebesar Rp 1.000.000,00 untuk menjalankan usahanya. Dia mematok harga krupuknya Rp 6.000,00 perbungkus. Jika Ia merencanakan ingin mendapat keuntungan Rp 200.000,00 dari hasil penjualannya, maka berapa kemasan krupuk minimal yang harus dibuat ?
Jawaban :
Jika ingin mendapatkan keuntungan sebesar Rp 200.000,00 maka total pendapatan hari itu adalah Rp 1.200.000,00.
Jadi, kemasan kerupuk yang harus dibuat adalah
Maka pedagang tersebut harus membuat 200 kemasan kerupuk jika ingin mendapat keuntungan sebesar Rp 200.000,00
10. VII Garis dan sudut 4.10. Menyelesaikan masalah yang berkaitan dengan hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal.
Sekilas Materi :
Garis adalah sekumpulan titik yang saling dihubungkan.
Sudut adalah sebuah daerah yang terbentuk karena adanya dua buah sinar garis yang titik pangkalnya saling berhimpit. 11. VII Luas dan keliling
segiempat dan segitiga.
4.11. Menyelesaikan masalah kontekstual yang berkaitan dengan luas dan keliling segiempat (persegi, persegi panjang, belah ketupat, jajargenjang, trapesium, dan layang-layang) dan segitiga. Sekilas Materi :
Persegi
Keliling = 4 sisi Luas = sisi sisi
Persegi Panjang
Keliling = 2(panjang + lebar) Luas = panjang lebar
Jajar Genjang Keliling =
2(sisi alas + sisi miring) Luas = alas tinggi
Trapesium
Keliling = jumlahan sisi-sisinya
Luas =
Keliling = 4 sisi miring Luas =
Layang-layang Keliling =
2(sisi terpendek + sisi terpanjang)
Luas =
Segitiga
Keliling = sisi alas + sisi tinggi + sisi miring
Luas =
12. VII Penyajian data 4.12. Menyajikan dan menafsirkan data dalam bentuk tabel, diagram, garis, diagram batang, dan diagram lingkaran.
Sekilas Materi :
Secara umum, ada 2 cara penyajian data yang sering digunakan, yaitu dengan tabel/daftar dan grafik/diagram.
Gambar 2.3. Diagram Lingkaran Acara Televisi
Sumber : Kemendikbud
13. VIII Pola bilangan 4.1. Menyelesaikan masalah yang berkaitan dengan pola pada barisan bilangan dan barisan konfigurasi objek.
Sekilas Materi :
Barisan bilangan adalah susunan bilangan yang memiliki pola tertentu.
Contohnya adalah barisan aritmetika dan barisan geometri.
Barisan konfigurasi objek adalah susunan bilangan yang terbentuk berdasarkan susunan dari suatu objek.
Contohnya adalah barisan dengan pola persegi, pola persegi panjang, pola segitiga, dan pola bilangan pascal.
14. VIII Koordinat kartesius
4.2. Menyelesaikan masalah yang berkaitan dengan kedudukan titik dalam bidang koordinat kartesius.
Sekilas Materi :
Koordinat kartesius digunakan untuk menentukan objek titik-titik pada suatu bidang dengan menggunakan dua bilangan yang biasa disebut dengan koordinat x dan koordinat y dari titik-titik tersebut.
Sumbu-X dan sumbu-Y membagi bidang kartesius menjadi 4 kuadran sebagai berikut.
Kuadran I : koordinat-x positif dan koordinat-y positif.
Kuadran II : koordinat-x negatif dan koordinat-y positif.
Kuadran III : koordinat-x negatif dan koordinat-y negatif.
Kuadran IV : koordinat-x positif dan koordinat-y negatif.
Contoh :
Titik P memiliki koordinat (-2,1) Maka -2 disebut koordinat-x Dan 1 disebut koordinat-y.
Maka titik P(-2,1) terletak di kuadran II.
15. VIII Relasi dan fungsi 4.3. Menyelesaikan masalah yang berkaitan dengan relasi dan fungsi dengan menggunakan berbagai representasi.
Relasi adalah hubungan antara suatu anggota himpunan dengan anggota himpunan lainnya.
Fungsi adalah relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B
16. VIII Persamaan garis lurus
4.4. Menyelesaikan masalah kontekstual yang berkaitan dengan linear sebagai persamaan garis lurus.
Sekilas Materi :
Persamaan garis lurus adalah persamaan yang membentuk garis lurus saat digambarkan dalam bidang kartesius.
Bentuk umum : y = mx + c Contoh : y = 2x + 1 17. VIII Sistem persamaan
linear dua variabel
4.5. Menyelesaikan masalah yang berkaitan dengan sistem persamaan linear dua variabel.
Sekilas Materi :
Sistem persamaan linear dua variabel (SPLDV) adalah suatu sistem yang terdiri dari persamaan-persamaan linear dua variabel.
Contoh :
Tia membeli 4 buku dan 8 pensil dengan harga Rp 50.000,00. Fany membeli 1 buku dan 10 pensil dengan harga Rp 36.500,00. Tentukan harga 1 buah buku dan 1 buah pensil.
Penyelesaian : Misalkan :
Harga 1 buah buku = x Harga 1 buah pensil = y
Maka, model matematikanya adalah
4x + 8y = 50.000 x + 10y = 36.500
Mencari harga 1 buah pensil Ubah persamaan 2 menjadi x = 36.500 – 10y
Kemudian substitusi persamaan tersebut ke persamaan 1 4x + 8y = 50.000 4(36.500 – 10y) + 8y = 50.000 146.000 – 40y + 8y = 50.000 146.000 – 32y = 50.000 146.000 – 50.000 = 32y 96.000 = 32y 3.000 = y
diperoleh harga 1 buah pensil yaitu Rp 3.000
Mencari harga 1 buah buku. x + 10y = 36.500
x + 10 (3.000) = 36.500 x + 30.000 = 36.500 x = 36.500 - 30.000 x = 6.500
maka diperoleh bahwa harga 1 buah buku adalah Rp 6.500
18. VIII Teorema Pythagoras
4.6. Menyelesaikan masalah yang berkaitan dengan teorema Pythagoras dan triple Pythagoras.
Sekilas Materi :
Teorema Pythagoras menyatakan bahwa
Untuk ABC, jika C adalah sudut siku-siku, maka
Triple Pythagoras adalah tiga bilangan asli yang memenuhi persamaan pada teorema Pythagoras.
Contoh :
Gambar 2.4. Persegi Panjang Sumber : Kemendikbud
Tentukan panjang EG dengan menggunakan teorema Pythagoras
Maka diperoleh panjang EG = Dari hal diatas, yang menjadi triple Pythagoras adalah 5, , 10. 19. VIII Lingkaran 4.7. Menyelesaikan masalah yang
berkaitan dengan sudut pusat, sudut keliling, panjang busur, dan luas juring lingkaran, serta hubungannya.
Sekilas Materi :
Lingkaran adalah kumpulan titik-titik yang membentuk garis lengkung yang memiliki jarak yang sama terhadap titik pusatnya.
Sudut keliling adalah sudut yang dibatasi oleh dua tali busur yang berpotongan di satu titik pada lingkaran dan titik sudutnya terletak pada keliling lingkaran..
Sudut pusat adalah sudut yang dibatasi oleh dua jari-jari lingkaran yang titik sudutnya merupakan titik pusat lingkaran.
Juring adalah daerah yang dibatasi oleh dua jari-jari lingkaran dan busur lingkaran.
Busur AB adalah garis lengkung AB.
20. VIII Garis singgung persekutuan luar dan persekutuan dalam dua lingkaran
4.8. Menyelesaikan masalah yang berkaitan dengan garis singgung persekutuan luar dan persekutuan dalam dua lingkaran.
Sekilas Materi :
Garis singgung persekutuan luar dua lingkaran adalah ruas garis terpendek yang menyinggung dua buah lingkaran dan tidak melalui daerah di antara kedua lingkaran.
Gambar 2.5. Garis Singgung Persekutuan Luar 2 Lingkaran
Sumber : Kemendikbud
Garis singgung persekutuan dalam dua lingkaran adalah ruas garis terpendek yang menyinggung dua buah lingkaran dan melalui daerah di antara kedua lingkaran.
Persekutuan Dalam 2 Lingkaran Sumber : Kemendikbud
21. VIII Bangun ruang sisi datar
4.9. Menyelesaikan masalah yang berkaitan dengan luas permukaan dan volume bangun ruang sisi datar (kubus, balok, prisma, dan limas), serta gabungannya. Sekilas Materi : Kubus Luas = 6 × Volume = Balok Luas = 2(pl + pt + lt) Volume =
panjang ×lebar × tinggi
Prisma
Luas = 2(luas alas) + jumlah luas bidang tegak
Volume = luas alas × tinggi
Limas
Luas = luas alas + jumlah luas bidang tegak
Volume =
× luas alas × tinggi
22. VIII Statistika 4.10. Menyajikan dan
menyelesaikan masalah yang berkaitan dengan distribusi data, nilai rata-rata, median,
modus, dan sebaran data untuk mengambil simpulan, membuat keputusan, dan membuat prediksi.
Sekilas Materi :
Ukuran Pemusatan Data :
Mean adalah rata-rata =
Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan.
Modus adalah nilai yang paling sering muncul dari suatu kumpulan data.
Ukuran Penyebaran Data :
Jangkauan adalah selisih antara nilai terbesar dan nilai terkecil dari suatu kumpulan data.
Kuartil Bawah ( )
Kuartil Tengah ( )
Kuartil Atas ( )
Jangkauan Interkuartil (H) adalah selisih antara nilai kuartil atas dan kuartil bawah dari suatu kumpulan data.
Simpangan Kuartil adalah setengah dari jangkauan interkuatil.
23. VIII Peluang 4.11. Menyelesaikan masalah yang berkaitan dengan peluang empirik dan teoretik suatu kejadian dari suatu percobaan.
Sekilas Materi :
Peluang Empirik adalah perbandingan antara frekuensi kejadian terhadap percobaan yang dilakukan.
Contoh : percobaan pelemparan uang logam.
Peluang Teoretik adalah perbandingan antara frekuensi kejadian yang diharapkan terhadap frekuensi kejadian yang mungkin.
24. IX Perpangkatan dan bentuk akar
4.1. Menyelesaikan masalah yang berkaitan dengan sifat-sifat operasi bilangan berpangkat bulat dan bentuk akar.
Sekilas Materi :
Perkalian Bilangan Berpangkat
Pemangkatan Bilangan Berpangkat
Pembagian Bilangan Berpangkat
Perpangkatan pada Bilangan Pecahan
25. IX Persamaan kuadrat 4.2. Menyelesaikan masalah yang berkaitan dengan persamaan kuadrat.
Sekilas Materi :
Bentuk Umum Persamaan Kuadrat dengan
dan Contoh :
26. IX Fungsi kuadrat 4.3. Menyajikan fungsi kuadrat menggunakan tabel, persamaan, dan grafik.
Sekilas Materi :
Bentuk Umum Fungsi Kuadrat dengan
dan Contoh : 27. IX Sifat-sifat fungsi kuadrat 4.4. Menyajikan dan menyelesaikan masalah kontekstual dengan menggunakan sifat-sifat fungsi kuadrat. Sekilas Materi :
Jika maka grafik terbuka ke atas.
Jika maka grafik terbuka ke bawah.
Jika maka parabola memotong sumbu X di dua titik.
Jika maka parabola menyinggung sumbu X di titik
– .
Jika maka parabola tidak memotong maupun menyinggung sumbu X.
28. IX Transformasi 4.5. Menyelesaikan masalah kontekstual yang berkaitan dengan transformasi geometri (refleksi, translasi, rotasi, dan dilatasi).
Sekilas Materi :
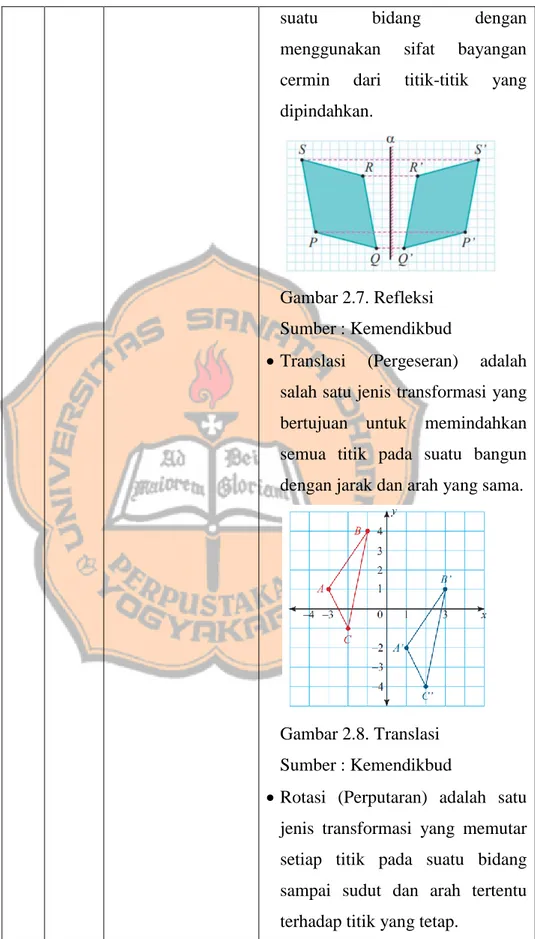
Refleksi (Pencerminan) adalah salah satu jenis transformasi yang memindahkan setiap titik pada
suatu bidang dengan menggunakan sifat bayangan cermin dari titik-titik yang dipindahkan.
Gambar 2.7. Refleksi Sumber : Kemendikbud
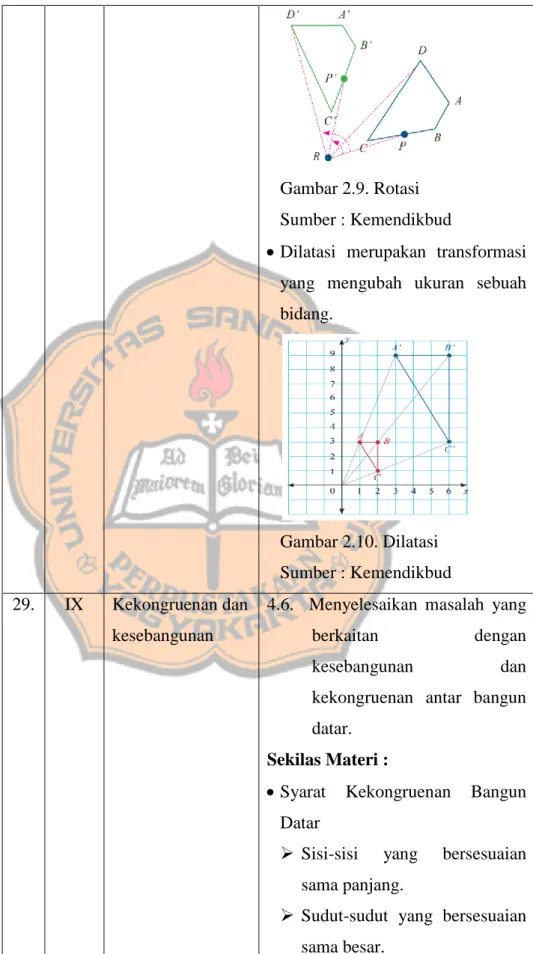
Translasi (Pergeseran) adalah salah satu jenis transformasi yang bertujuan untuk memindahkan semua titik pada suatu bangun dengan jarak dan arah yang sama.
Gambar 2.8. Translasi Sumber : Kemendikbud
Rotasi (Perputaran) adalah satu jenis transformasi yang memutar setiap titik pada suatu bidang sampai sudut dan arah tertentu terhadap titik yang tetap.
Gambar 2.9. Rotasi Sumber : Kemendikbud
Dilatasi merupakan transformasi yang mengubah ukuran sebuah bidang.
Gambar 2.10. Dilatasi Sumber : Kemendikbud 29. IX Kekongruenan dan
kesebangunan
4.6. Menyelesaikan masalah yang
berkaitan dengan
kesebangunan dan
kekongruenan antar bangun datar.
Sekilas Materi :
Syarat Kekongruenan Bangun Datar
Sisi-sisi yang bersesuaian sama panjang.
Sudut-sudut yang bersesuaian sama besar.
Gambar 2.11. Dua Bangun Kongruen
Sumber : Kemendikbud
Syarat Kesebangunan Bangun Datar
Sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
Sudut-sudut yang bersesuaian sama besar.
Gambar 2.12. Dua Bangun Sebangun
Sumber : Kemendikbud 30. IX Bangun ruang sisi
lengkung
4.7. Menyelesaikan masalah kontekstual yang berkaitan dengan luas permukaan dan volume bangun ruang sisi lengkung (tabung, kerucut, dan bola) serta gabungan beberapa bangun ruang sisi lengkung.
Tabung Luas = Volume = Kerucut Luas = Volume = Bola Luas = Volume =
B. Penelitian yang Relevan
Beberapa penelitian yang relevan terkait dengan pengkajian aktivitas fundamental matematis menurut Bishop, meliputi :
1. Penelitian yang dilakukan oleh Supriatna dan Nurcahyono (2017). Penelitiannya berjudul “Etnomatematika : Pembelajaran Matematika Berdasarkan Tahapan-tahapan Kegiatan Bercocok Tanam”. Aspek matematis pada tahapan-tahapan kegiatan bercocok tanam adalah sebagai berikut :
a. Pengolahan lahan : terdapat aspek matematis berupa geometri seperti persegi panjang dalam pembuatan bedengan dan perbandingan yaitu perbandingan luas lahan dengan waktu pengolahan lahan.
b. Seleksi benih tanaman : terdapat aspek matematis berupa persentase yaitu persentase antara benih yang layak tanam dan tidak layak tanam.
c. Penanaman : terdapat aspek matematis berupa perbandingan yaitu perbandingan antara jarak tanam dengan luas lahan.
d. Perawatan : terdapat aspek matematis berupa operasi bilangan bulat yaitu menghitung jumlah benih yang tumbuh dan tidak tumbuh.
e. Panen : terdapat aspek matematis berupa perhitungan dan penyajian data seperti menghitung rata-rata hasil panen dan menyajikannya dalam tabel atau diagram.
2. Penelitian yang dilakukan oleh Rani (2018). Penelitiannya berjudul “Etnomatematika pada Candi Ratu Boko Sebagai Pendukung Pembelajaran Matematika Realistik”. Aspek matematis pada Candi Ratu Boko adalah sebagai berikut :
a. Gerbang Candi Ratu Boko : terdapat aspek matematis berupa geometri yaitu bangun datar segitiga.
b. Candi Kapur Ratu Boko : terdapat aspek matematis berupa geometri yaitu bangun datar persegi.
c. Candi Pembakaran : terdapat aspek matematis berupa geometri yaitu bangun datar trapesium.
d. Paseban Candi Ratu Boko : terdapat aspek matematis berupa geometri yaitu bangun datar persegi panjang.
Dari semua hal tersebut, dapat diperoleh luas dan kelilingnya.
3. Penelitian yang dilakukan oleh Nisa, Nurjamil, Muhtadi, Sukirwan (2019). Penelitiannya berjudul “Studi Etnomatematika pada Aktivitas Urang Sunda dalam Menentukan Pernikahan, Pertanian dan Mencari Benda Hilang”. Aspek matematis yang dibahas dalam penelitian tersebut, yakni :
a. Terdapat aspek matematis berupa operasi bilangan bulat dalam menjumlahkan weton.
b. Terdapat konsep modulo dalam penentuan hari baik.
C. Kerangka Berpikir
Masih banyak siswa yang beranggapan bahwa matematika adalah ilmu yang tidak mudah dipahami karena dirasa kurang implementatif. Padahal, kenyataannya matematika melekat pada setiap aspek kehidupan dan berperan sangat penting dalam kehidupan manusia. Mengingat pentingnya matematika dalam kehidupan maka, munculah ide untuk mengenalkan matematika
melalui kegiatan yang ada dalam kehidupan nyata. Kegiatan tersebut adalah budidaya jamur tiram. Pada budidaya jamur tiram terdapat aktivitas-aktivitas yang berkaitan dengan matematika. Maka, melalui enam aktivitas fundamental matematis menurut Bishop, peneliti akan menganalisis aspek matematis pada kegiatan budidaya jamur tiram. Aspek matematis yang ditemukan akan digunakan untuk membuat permasalahan kontekstual dari budidaya jamur tiram.
Berikut bagan kerangka berpikir yang peneliti buat :
44 BAB III
METODE PENELITIAN
A. Jenis Penelitian
Jenis penelitian yang digunakan merupakan penelitian deskriptif dengan pendekatan kualitatif. Menurut Moleong (2007: 6), penelitian kualitatif adalah penelitian yang bermaksud untuk memahami fenomena tentang apa yang dialami oleh subjek penelitian misalnya perilaku, persepsi, motivasi, tindakan, dan lain-lain secara holistic, dan dengan cara deskripsi dalam bentuk kata-kata dan bahasa, pada suatu konteks khusus yang alamiah serta dengan memanfaatkan berbagai metode alamiah. Peneliti menggunakan penelitian kualitatif karena dalam penelitian ini, proses deskripsi akan dilakukan dengan memaparkan hasil wawancara dengan narasumber.
B. Narasumber Penelitian
Narasumber dalam penelitian ini adalah pemilik usaha budidaya jamur tiram sekaligus penjual produk olahan jamur tiram yaitu Pak Bernadus Bagus Supranyoto. Peneliti memilih Pak Bagus sebagai narasumber karena skala usaha budidaya jamur yang dimiliki Pak Bagus sudah berskala besar sehingga langkah-langkah budidaya jamur yang dilakukan lebih lengkap.
C. Objek Penelitian
Objek dalam penelitian ini adalah aspek matematis dan permasalahan kontekstual dari budidaya jamur tiram.
D. Tempat dan Waktu Penelitian 1. Tempat Pengambilan Data
Penelitian dilaksanakan di Dusun Beran Kidul, Tridadi, Kabupaten Sleman, Daerah Istimewa Yogyakarta.
2. Waktu Penelitian
Tahap Waktu Kegiatan
1 4 Oktober - 15 Oktober 2019 Observasi Penelitian
2 16 Oktober - 6 Desember 2019 Pembuatan Proposal Penelitian 3 24 Februari – 23 Maret 2020 Persiapan
4 17 April - 30 April 2020 Pelaksanaan Penelitian 5 1 Mei – 22 Mei 2020 Analisis Data
6 23 Mei – 24 Mei 2020 Penarikan Kesimpulan 7 25 Mei – 7 Juni 2020 Penulisan Hasil Penelitian 8 9 Juni – 27 Juli 2020 Penyempurnaan laporan
E. Bentuk Data
Data dalam penelitian ini, diperoleh dari hasil observasi, hasil wawancara dengan narasumber, dan hasil dokumentasi terkait proses budidaya jamur tiram. Maka bentuk data yang digunakan adalah data deskriptif berupa kata-kata tertulis atau lisan dari orang-orang dan perilaku yang dapat diamati seperti apa yang diungkapkan Bogdan dan Taylor (1975) yang dikutip oleh Moleong (2007:4).
F. Metode Pengumpulan Data
Metode pengumpulan data yang digunakan dalam penelitian ini adalah observasi, wawancara, dan dokumentasi yang dipaparkan sebagai berikut : 1. Observasi
Observasi yang dilakukan bertujuan untuk mencari informasi terkait proses budidaya jamur tiram yang nantinya akan digunakan untuk menentukan apa saja aspek-aspek matematis yang terdapat pada aktivitas budidaya jamur tiram.
2. Wawancara
Wawancara yang dilakukan bertujuan untuk menggali informasi secara detail. Wawancara bersifat terbuka dan fleksibel dimana
pertanyaan-pertanyaan yang diberikan kepada narasumber sudah mengacu pada pedoman wawancara yang telah disiapkan tetapi, tidak menutup kemungkinan akan ada pertanyaan tambahan jika dirasa masih ada yang perlu untuk ditanyakan.
3. Dokumentasi
Dokumentasi yang dilakukan dalam penelitian ini, bertujuan untuk menunjang data hasil observasi dan wawancara untuk menyimpulkan hasil penelitian. Dokumentasi yang dilakukan meliputi pengambilan foto dan rekaman suara.
G. Instrumen Pengumpulan Data
Instrumen pengumpulan data dalam penelitian ini adalah peneliti, pedoman observasi dan pedoman wawancara.
1. Peneliti
Peneliti sebagai instrumen utama yang digunakan untuk memperoleh data pokok sesuai tujuan penelitian. Dalam hal ini, peneliti diharapkan dapat menetapkan fokus penelitian, menentukan narasumber yang tepat sebagai sumber data, melakukan pengumpulan data, menganalisis data dan membuat kesimpulan dari temuan yang didapatkan.
2. Pedoman Observasi
Menurut Sugiyono (2011:121) pedoman observasi digunakan apabila obyek penelitian bersifat perilaku manusia, proses kerja, gejala alam, responden kecil. Maka pedoman observasi dalam penelitian ini digunakan untuk mengamati setiap proses budidaya jamur tiram yang memuat aktivitas fundamental matematis. Pedoman observasi yang dibuat berisi kisi-kisi (lampiran 5, halaman 82) dan daftar-daftar pernyataan (lampiran 6, halaman 84) yang akan digunakan untuk menggali aspek matematis pada tahapan-tahapan budidaya jamur tiram. Pedoman observasi yang digunakan merupakan pedoman observasi yang berupa check list, dimana peneliti telah memilih dan mendefinisikan hal yang akan diamati sebelum observasi dilaksanakan sehingga ketika observasi, peneliti hanya perlu
memberikan tanda ceklis apabila hal yang diamati sesuai dengan pernyataan yang disajikan.
3. Pedoman Wawancara
Pedoman wawancara digunakan apabila ingin mengetahui hal-hal dari responden secara lebih mendalam serta dengan jumlah responden yang sedikit (Sugiyono, 2011:121). Pedoman wawancara dalam penelitian ini berisi kisi-kisi (lampiran 2, halaman 73) dan daftar pertanyaan (lampiran 3, halaman 77) yang akan dijadikan acuan dalam menggali informasi dari narasumber terkait aspek matematis pada tahapan-tahapan budidaya jamur tiram di Dusun Beran Kidul, Tridadi, Kabupaten Sleman, Yogyakarta. Wawancara dilakukan dengan pemilik usaha budidaya jamur tiram. Pertanyaan yang disajikan adalah tipe pertanyaan tidak terstruktur, yang berarti setiap pertanyaan tidak terikat pada jawaban dari pertanyaan sebelumnya (Sugiyono, 2011:138).
H. Teknik Analisis Data
Analisis data kualitatif dilakukan apabila data empiris yang diperoleh adalah data kualitatif berupa kumpulan berwujud kata-kata dan bukan rangkaian angka serta tidak dapat disusun dalam kategori-kategori/struktur klasifikasi. Menurut Moleong (2007), kegiatan analisis terdiri dari empat alur kegiatan, yaitu reduksi data, kategorisasi, sintesisasi, dan penyusunan hipotesis kerja.
Analisis data kualitatif menurut Moleong terdapat 4 (empat) tahap, dipaparkan sebagai berikut :
1. Reduksi Data
Reduksi data diartikan sebagai proses pemilihan, pemusatan perhatian pada penyederhanaan, pengabstraksian, dan transformasi data kasar yang muncul dari catatan-catatan tertulis di lapangan. Proses reduksi data yang dilakukan peneliti adalah mempelajari dan memeriksa data yang diperoleh di lapangan kemudian membuat rangkuman pada setiap pertemuan dengan narasumber. Setelah itu, peneliti menseleksi data dan mengorganisasi data
sedemikian rupa sehingga data yang dimiliki berkaitan dengan fokus penelitian.
2. Kategorisasi
Kategorisasi merupakan teknik analisis data yang bertujuan untuk memilah setiap data yang saling berkaitan maupun yang memiliki kesamaan fokus permasalahan. Pada langkah ini, peneliti berusaha mengelompokkan data yang relevan sehingga menjadi informasi yang dapat disimpulkan dan memiliki makna tertentu. Dalam hal ini, peneliti juga mengaitkan fenomena-fenomena yang terjadi di lapangan dengan data yang diperoleh dari narasumber.
3. Sintesisasi
Sintesis data artinya mencari kaitan atau hubungan antar kategori yang telah ditemukan. Pada tahap ini, peneliti mengamati keterkaitan antar kategori yang diperoleh dengan aspek-aspek matematis.
4. Menyusun Hipotesis Kerja
Hipotesis kerja digunakan untuk menjawab rumusan masalah dalam penelitian ini. Hasil yang didapat pada tahap ini akan menjadi sebuah kesimpulan yang bersifat final. Dalam menyusun hipotesis kerja, peneliti melihat hasil analisis data yang sudah dilakukan dan pembahasannya.
I. Prosedur Pelaksanaan Penelitian
Prosedur pelaksanaan ini adalah sebagai berikut : 1. Tahap Persiapan
a. Menyusun rancangan penelitian terkait proposal penelitian yang telah disetujui
b. Memilih lokasi penelitian. Lokasi budidaya jamur tiram di Dusun Beran Kidul, Tridadi, Sleman, Yogyakarta menjadi lokasi pilihan peneliti.
c. Membuat pedoman observasi dan pedoman wawancara. d. Memilih narasumber penelitian.
e. Menyiapkan peralatan untuk menunjang proses wawancara dan observasi seperti perekam suara dan kamera.
2. Tahap Pengumpulan Data
a. Peneliti melakukan observasi ke lokasi budidaya jamur tiram. Pada kegiatan ini, peneliti mencatat hal-hal penting yang ditemukan dan mendokumentasikan objek penelitian.
b. Selanjutnya, peneliti melakukan kegiatan wawancara dengan narasumber yang telah ditetapkan menggunakan pedoman yang telah disiapkan. Dalam hal ini, peneliti menggali semua informasi yang dibutuhkan dan mencatat hal-hal pokok selama proses wawancara berlangsung.
c. Untuk memperkuat analisis data, peneliti juga mencari informasi dari berbagai sumber seperti buku dan petani terkait aktivitas budidaya jamur tiram.
3. Tahap Analisis Data
Setelah mendapatkan data dari hasil observasi dan wawancara, peneliti menganalisis dan melakukan proses reduksi data. Tahap ini dilakukan bersamaan dengan proses pengumpulan data. Tujuannya adalah agar proses penelitian dapat lebih terarah dan apabila terjadi kekurangan data maka proses pencarian data dapat dilakukan kembali pada hari selanjutnya.
4. Tahap Penarikan Kesimpulan
Pada tahap ini, peneliti mengaitkan hasil analisis data yang diperoleh dengan aspek-aspek matematis. Lalu peneliti menarik kesimpulan dari hasil analisis dan pembahasan untuk menjawab rumusan masalah yang telah dibuat.
50 BAB IV
HASIL DAN PEMBAHASAN
A. Pelaksanaan Penelitian
Penelitian dilakukan di Rumah Kebun Jamur yang terletak di dusun Beran Kidul, Tridadi, Sleman, Yogyakarta. Pada bulan Maret 2020, penelitian di awali dengan melakukan observasi dan wawancara terbuka kepada beberapa orang yang memiliki usaha budidaya jamur tiram, yang bertujuan untuk melihat dan mengetahui apakah terdapat aspek matematis yang diterapkan dalam proses budidaya jamur tiram. Hasil dari observasi dan wawancara tersebut, didapat beberapa aspek matematis dalam proses budidaya jamur tiram, maka peneliti memutuskan untuk melanjutkan penelitian secara lebih mendalam.
Sebelum terjun ke lapangan untuk melakukan penelitian, peneliti terlebih dahulu mempersiapkan hal-hal yang dibutuhkan untuk menunjang proses penelitian seperti mempersiapkan instrumen penelitian yaitu pedoman observasi dan pedoman wawancara. Pedoman observasi dan wawancara akan digunakan peneliti untuk mengumpulkan data penelitian. Pertanyaan dan pernyataan yang ada dalam pedoman wawancara dan pedoman observasi berkaitan dengan aktivitas fundamental matematis yang terdapat pada proses budidaya jamur tiram. Pedoman observasi dan wawancara yang telah dibuat peneliti kemudian diserahkan kepada dosen pembimbing untuk diperiksa. Setelah diperiksa dan disetujui oleh dosen pembimbing, peneliti melakukan validasi instrumen kepada validator. Setelah divalidasi dan instrumen dianggap layak untuk digunakan, maka peneliti dapat melanjutkan penelitian untuk pengambilan data.
Pengambilan data dilakukan pada bulan April 2020. Pengambilan data dilakukan dengan melakukan wawancara kepada pemilik usaha budidaya jamur tiram secara daring melalui aplikasi Whatsapp, dikarenakan pandemi Covid-19.
B. Penyajian Data
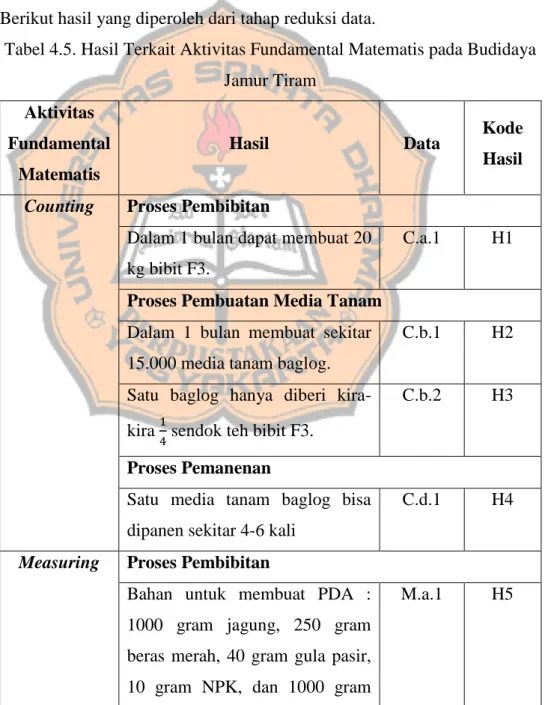
1. Data Hasil Wawancara
a. Aktivitas Counting pada Proses Budidaya Jamur Tiram
Peneliti akan memberi kode C untuk data aktivitas counting. Pada aktivitas ini, peneliti menemukan aktivitas counting pada beberapa proses dalam budidaya jamur tiram. Maka peneliti akan memberikan kode untuk aktivitas counting pada beberapa proses tersebut. Kode tersebut akan dijabarkan sebagai berikut :
1) Kode a digunakan untuk data yang menunjukkan aktivitas
counting pada proses pembibitan.
2) Kode b digunakan untuk data yang menunjukkan aktivitas
counting pada proses pembuatan media tanam.
3) Kode c digunakan untuk data yang menunjukkan aktivitas
counting pada proses pemeliharaan.
4) Kode d digunakan untuk data yang menunjukkan aktivitas
counting pada proses pemanenan.
5) Kode e digunakan untuk data yang menunjukkan aktivitas
counting pada proses produksi hasil olahan.
6) Kode f digunakan untuk data yang menunjukkan aktivitas
counting pada proses pendistribusian
Kode data aktivitas counting akan diberi kode C.(kode huruf).(nomor urut). Misalnya kode C.a.1 menjelaskan tentang data wawancara aktivitas counting pada proses pembibitan urutan pertama. Kode N merupakan kode untuk narasumber. Kode P merupakan kode untuk peneliti.
Berikut adalah tabel data aktivitas counting dari hasil wawancara : Tabel 4.1. Data Aktivitas Counting pada Proses Budidaya Jamur
Tiram
Data Kode Data Subyek
P : Berapa jumlah media pembibitan yang dapat dibuat dalam 1 bulan ?
N : Sebenarnya tidak menentu, tergantung berapa banyak permintaan baglog. Tetapi biasanya setiap bulan, kami membuat kurang lebih 20 kg F3. Bibit F3 adalah bibit yang nantinya akan dimasukkan ke dalam baglog.
P : Berapa jumlah media tanam yang dapat dibuat dalam 1 bulan ?
N : Setiap bulan biasanya kami bisa membuat sekitar 15.000 media tanam baglog. Peminat untuk baglog ini sangat banyak sekali. Biasanya petani lebih memilih untuk membeli baglog daripada membuatnya sendiri.
C.b.1 N
P : Berapa jumlah bibit yang diperlukan dalam satu media tanam ?
N : Satu baglog hanya diberi kira-kira sendok teh bibit F3. Tetapi jika baglog yang dibuat lebih besar ukurannya, maka jumlah F3 yang dimasukkan ke dalam baglog juga lebih banyak.
C.b.2 N
P : Berapa kali proses pemanenan yang dapat dilakukan dari satu media tanam ? N : Dari satu media tanam baglog itu bisa dipanen sekitar 4-6 kali.
C.c.1 N
b. Aktivitas Measuring pada Proses Budidaya Jamur Tiram
Peneliti akan memberi kode M untuk data aktivitas measuring. Pada aktivitas ini, peneliti menemukan aktivitas measuring pada setiap proses dalam budidaya jamur tiram. Maka peneliti akan memberikan