CHAPTER I...1
INTRODUCTION...1
A. Background...1
B. Research Problem...4
C. Research Objective...4
D. Research Benefits...4
E. Term Limit...4
CHAPTER II...6
LITERATURE RIVIEW...6
A. Theory Riview...6
B. Relevant Research...24
C. Fremework...27
CHAPTER III...29
RESEARCH METHODS...29
A. Type of research...29
B. Research Subject...29
C. Research Procedures...30
D. Research Instrument...32
E. Data Analysis Techniques...33
F. Quality Standard of Qualitative Research...35
A. Background
B. Science is the key to all the problems of both lives in the world and the hereafter. Science is very influential in our lives, with the science created objects that can facilitate our work, with the science we can manage the natural resources that exist around, with science we also do charity. One way to study is through formal education. Formal education is a structured educational pathway of basic education, secondary education, and higher education.
C. The quality of education in a country is one of supporting the development of the country. One of the problems of education in Indonesia is that students have not been able to compete with the students of other countries when the demands of competition in the field of education are very necessary for the young generation in the era of the ASEAN Economic Community. Education Indonesia should be able to prepare graduates who are able to overcome the competition.
E. According to NCTM (2000: 7), in mathematics learning there are five process standards: problem-solving, reasoning and prof, communication (communication), connection), and representation (presentation). Students are required to have the ability to count only, but also must have the ability to reason, logical, and critical in solving the problem. This is in line with TIMSS demands involving knowledge, application, and reasoning in learning mathematics.
F. Mathematics is one of the areas of study that occupy an important role in education. This is shown from the implementation of mathematics education given to all levels of education ranging from elementary school to higher education and even in college. Mathematics is also important to learn because math is never out of human life. One of the subjects that became the focus of the TIMSS assessment was mathematics, in mathematics, there are two domains of the content domain and cognitive domain. One of the subdomains in the content domain is Geometry. The average percentage of true Indonesian students in sub-geometry domains is 24% lower than the international average of 39%.
H. In solving the word problem is not only required the ability to calculate it but also needed reasoning power, therefore students sometimes have difficulty. The difficulties experienced by the students allow for mistakes in working on the word problem. Therefore, the errors experienced by students in solving the word problem is considered necessary to be analyzed so that errors are often done by students can be known so that teachers can provide appropriate assistance to students. There are some mistakes that are often done when students do the word problem is: First the students sometimes wrong in reading and understanding the problem. Both students already understand the problem but have not captured the important information contained in the matter so that students do not know what is asked and that is known in the matter. The three students have difficulty in changing the word problem into the form of the mathematical model, and the students are wrong in determining the problem-solving strategy. The four students wrong in performing the count operation. The five students are wrong in the writing of the answer or the student is wrong in summing up the final result.
J. Based on the description above, to know the possible mistakes of students in solving the word problem on geometry material, encouraging writers to conduct research entitled " Analysis of Students’ Error in Solving Geometry Word Problems Based on Newman’s Prosedures".
K. Research Problem
L. Based on the above background description, the problem to be discussed in this research is "How to profile the students' error in solving the geometry word problems based on Newman's error analysis procedure?". M. Research Objective
N. From the above problem formulation, it can be concluded that the goal to be achieved in this research is "Knowing the profile of student error in solving the geometry word problem based on Newman's error analysis procedure".
O. Research Benefits
P. The expected benefits of this research are as follows:
1. Increase the writer's insight about the difficulties experienced by students’ in solving the word problem.
2. Can provide stock for the author as a prospective educator.
3. Teachers can use as one of the materials in creating a better learning process.
4. Increase teacher's knowledge especially about students' difficulties in solving word problems.
Q. Term Limit
R. To avoid different interpretations against the terms used in this research, it is necessary given the limitations of the term as follows:
1. An analysis is an investigation of an event to know the real situation. In this case, the investigation is about the students' mistakes in solving the word problem that related to the geometry material. So it can be known the cause of errors committed by students.
2. Mistakes in this study are errors made by students in solving the word problem that includes the type of error. The type of error in question is an error based on Newman's procedure of reading errors can be called Type R errors, comprehension errors can be called Type C errors, transformation errors can be called T Type errors, process skills can be called Type P errors, and encoding errors can be called Type E errors.
A. Theory Riview
1. The nature of mathematics
B. Mathematics is part of a definite science (exacta) apparently has its own origins. Mathematics comes from the Latin word "mathematika" originally derived from the Greek word "mathematike" meaning "knowledge, though, learning". According to Big Indonesian Dictionary (KBBI), mathematics is defined as the science of, the relationship between numbers, and operational procedures used in solving problems concerning numbers.
C. Another form of mathematics is a very symbolic language (Rashid, 2000: x). Haryono (2014: 118) suggests that:
D. "Math and language have the same meaning and function. If mathematics is used as a tool that unites humans in numeracy, then language is also a tool for uniting human beings in communicating, but language is universal which is used by certain countries that use their respective languages while the mathematics of all countries use it, if a country declares 2 + 2 = 4 then in another country. "
E.
F. Based on the blurb Haryono (2014:118) defines that mathematics is the national language. Things that were revealed by Tyro (2010:22) that mathematics is a language that is very symbolic, representing a series of meanings that want to be delivered.
G. Murtadho and Tambunan (1987: 2.4) state that:
H. “one of the essential elements in the teaching of mathematics is mathematics itself. A teacher of mathematics must know the object that is taught that is math. What is math?”
I.
a. Mathematics is the knowledge of quantity and space, one of the branches of many sciences, systematic, orderly and exact.
b. Mathematics is the numbers and calculations that are part of human life. c. Mathematics is the knowledge or science of logic and numerical problems. d. Mathematics is the queen of science.
e. Mathematics is a measuring instrument and does not lie in the social sciences, economics, and technology (mathematics is the queen of all sciences, servants of all sciences).
K. It can not be denied that there are many more definitions expressed by experts on mathematics. From the above definitions can at least provide an overview of the understanding of the math itself. Mathematics can be viewed from different angles and mathematics itself can enter various aspects of human life ranging from the simplest to the most complicated things, therefore all the above definitions are acceptable.
2. Word problem
L. In Kamus Besar Bahasa Indonesia (KBBI) the problem is defined as what demands answers and so on (questions in the count) or things to be solved. While the story is defined as a speech that unfolds how the occurrence of a thing (events, events, etc.) or articles that tell the deed, the experience or both the suffering of people, whether real or imaginary or manifestation of the play or embodied in the live image. Therefore the question of the word problem can be interpreted as a form of problems relating to an event, events and so forth which is usually related to problems in everyday life that demands answers or solutions to the problem.
M. In Big Indonesian Dictionary (KBBI), an analysis is interpreted as an investigation on an event (essay, action and so on) to find out what the causes, how to sit the case, and so forth. While mistakes are defined as being wrong, mistakes, and omissions. Therefore the analysis of error can be interpreted as an investigation of the act of deviating or error by finding out what the causes of the occurrence.
N. Analysis of errors in this study is the investigation of irregularities or mistakes made by students who are systematic in solving the word problem of mathematical.
4. The types and categories of errors in mathematics
O. In the Large Indonesian Language Dictionary (KBBI) error refers to a confusion or forgetfulness. In this case, the confusion or forgetfulness can be done accidentally or intentionally. There are several elements that influence the incidence of errors, such as students, faculty, learning methods, the environment and others.
P. According to Hadar et al (1987) errors can be classified as follows:
a. Data errors, data errors associated with a mismatch between known data and data cited by students.
b. Error interpreting language.
c. Errors using logic in drawing conclusions. d. Error using definition or theorem.
e. Resolution is not checked again. f. Technical problem.
Q. Radatz (in Padmavathy: 2015) classifies errors based on information obtained from students and classifies the categories as follows:
a. Mistakes due to lack of mastering prerequisite, fact, and concept skills. b. Error due to wrong or rigid in thinking.
R. Newman's error analysis method was first introduced in 1997 by Anne Newman, a mathematics teacher in Australia. With this method, Newman suggests five specific activities as a very helpful to find where the errors that occur in the student's work when solving a word problem. Newman's error analysis was designed as a simple diagnostic procedure. Newman (in White, 2010) states that when a person tries to answer work problems mathematical it must pass several obstacles in sequence: level 1 Reading, level 2 Comprehension, level 3 Transformation, level 4 Process Skills, level 5 Encoding. Of the five activities above that must be done by the students while solving the word problems, Newman (in White, 2010) listed the interview instructions for the method of analysis as follows: a. Please read the question to me. If you don’t know a word, leave it out. b. Tell me what the question is asking you to do.
c. Tell me how you are going to find the answer.
d. Show me what to do to get the answer. “Talk aloud” as you do it so that I can understand how you are thinking.
e. Now, write down your answer to the question.
S. With these questions then the type of error and the cause of student error when solving the math word problem can be found. As for the indicator of the type of error based on Newman's procedure (in Clements, 1980) and the same thing that indicates the type of student error based on Newman's procedure (in faith in Ekayanti, 2017) as shown in the following table:
Comprehension
errors
Students can already understand the problem but have not captured the information contained in the question Students do not know what is known or
what is in the problem Transformation
errors
Students fail to understand the problems to be transformed into correct mathematical sentences
The student is wrong in determining problem solving strategy
Process skill errors Error in process skills
The student is wrong in using the rules or rules are correct
Error in calculation or computation AA. Encoding errors Error writing the final answer
Error in using the notation
Errors due to careless or inadequate
BB. From the above explanation, it can be said that there are no guidelines or standards that become references to determine or classify students' mistakes in doing math problems. Since this study uses math word problems so that researchers choose to use the classification in accordance with it. As revealed by White (2010) that Newman's Error Analysis (NEA) is suitable for classification in diagnosing students' mistakes in solving word problems mathematics. Therefore in this study, the researchers used the procedure Newman in analyzing student error.
5. The Definition Of Geometry
line and space objects and their properties, their sizes and their relationships with each other.
DD.Usiskin (Prasetio, 2012) states that:
i. Geometry is a branch of mathematics that studies visual patterns.
ii. Geometry is a branch of mathematics that links mathematics to the physical world or the real world.
EE. Van Hiele (in Prasetio, 2012) states that:
i. Geometry is the presentation of abstractions from visual and spatial experiences, such as fields, patterns, measurements, and mappings.
ii. Geometry provides approaches to problem solving, such as drawings, diagrams, coordinate systems, vectors, and transformations.
FF. In the mathematics geometry are mind-objects that have perfect shape and size. Geometric objects are objects of thought derived from real objects that are abstracted and idealized. abstracted is not considered the color, odor, temperature and other properties and idealized that is considered perfect. Objects in geometry are abstract, meaning they are mind objects where they can only be imagined in the mind, although they can be represented in the form of models or props, in fact, they represent only a few properties of objects by removing the ideal properties of the object itself. The objects of geometry are the points, plane, angle, triangle, and other geometry constructs in which they are objects "perfect" within the frame of mind of Euclid.
are required to be ready for a deductive geometry curriculum at high school, it is important for learners' thinking to develop at level 2 (informal deduction) at the end of grade VIII (Van De Walle, 2008: 155).
HH.Geometry is one of the material that is considered important in mathematics. Usiskin (in Safrina, 2014) gives a reason why geometry needs to be taught ie first, the geometry of the only field of mathematics that can relate mathematics to the physical form of the real world. Second, the only geometry that can allow mathematical ideas to be visualized, and third, geometry can provide a non-singular example of a mathematical system.
II. It is necessary to distinguish between geometrical knowledge by thinking geometry. Knowledge of geometry is information (concept) owned by someone based on his logical observation about matters relating to geometry. Knowledge of the geometry of the students is influenced by the mastery of the concept. The less the concept of student geometry means the lower the knowledge of the geometry of the student. While thinking geometry is one's ability to explore, provide logical reasons, and solve problems about geometry. Think geometry has several levels from the lowest level to the highest level.
6. Mathematics material in junior high school
ability. Therefore, in learning geometry, the material should be sequential and not skip, the most important in geometry is basic understanding. With a solid foundation, it will be easier to develop and expand understanding of geometry learning. At the junior level students are expected to be able to develop a systematic problem-solving plan in order to group the objects into classes and subclasses.
KK.Geometric objects are abstract mind objects, then mastering the concept for each teacher is very important. The teacher must always sharpen the understanding of geometric concepts taught because the mistakes of teacher concepts will lead to the concepts of students who will be the source of difficulty or error in solving geometry problems. Based on the curriculum 2013 (K13) mathematics material taught to junior high school students can be seen in Table 2 below:
LL. Tabel 2. Mathematics material in junior high school
MM. Class NN. Materi
OO. Class VII
a. Set b. Numbers
c. Triangles and Four-side plane figure d. Ratio and propertions
e. Linear equations and linear inequalities in one variable
f. Social arithmetic g. Transformations
PP. Class VIII a. Algebraic expressions
b. Function
c. Linear Equations
d. Linear equations in two variable e. Coordinate System
f. Quadratic equation g. Comparison
j. sSolid figure k. Statistics l. Probability
QQ. Class IX
a. exponential number and root shape b. Quadratic functions and equations
i. Number pattern, sequence and series RR.
SS. Basically, the purpose of learning geometry at the junior level is so that students can understand the properties and relationships between elements of geometry and can be a good problem solver in solving mathematical problems, especially geometry that has an abstract object of study. Although in fact, geometry material has been known to students since elementary school, junior high school students often experience difficulties when faced with this material, one of the material that has been studied by the students of junior high school class VIII is triangle and rectangle.
TT. UU.
7. Triangle and rectangle
a. Triangle
VV. Polygons are closed sealed waves bounded by sides in the form of segments of straight-line segments. Djadir, Minggi, Ja'faruddin, Zaki, Sidjara (2017) mentioned that "Triangle is a polygon with three sides". Further according to Team Geometry "triangle is a combination of three
A
C
segments of a line formed by three non-aligned points with which the two are interconnected." Can be seen in the following figure:
WW. figure 1. Triangle ABC XX.
YY. Figure 1 is a figure of an ABC triangle can be symbolized by ΔABC . AB´ , BC´ , and AC´ is called the triangle side ABC.
The three sides of the triangle which intersect form an angle, ie ∠A, ∠B, and ∠C. Thus, a triangle has three angles and three sides. Triangle has several types. The types of triangles can be reviewed on the basis of the following elements. Figure 1 is a picture of an ABC triangle that can be symbolized by ΔABC. . AB´ , BC´ , and AC´ is called the triangle side ABC. The three sides of the triangle which intersect form an angle, ie ∠A, ∠B, and ∠C . Thus, a triangle has three angles and three sides.
Triangle has several types. The types of triangles can be reviewed on the basis of the following elements:
ZZ.
i. Types of triangles by relative lengths of their sides
AAA. Triangles can be classified according to relative lengths of their sides. The three types of triangles are as follows:
1. Scalene triangle
BBB. a scalene triangle is a triangle whose trhee sides are not equal in length. ∆ ABC in figure 2 below is a scalene triangle.
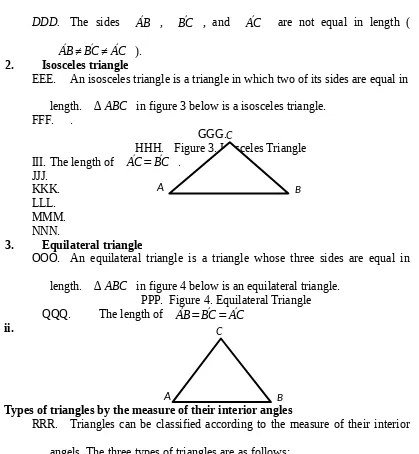
DDD. The sides AB´ , BC´ , and AC´ are not equal in length ( ´
AB ≠BC ≠´ AC´ ). 2. Isosceles triangle
EEE. An isosceles triangle is a triangle in which two of its sides are equal in length. ∆ ABC in figure 3 below is a isosceles triangle.
FFF. .
OOO. An equilateral triangle is a triangle whose three sides are equal in length. ∆ ABC in figure 4 below is an equilateral triangle.
PPP. Figure 4. Equilateral Triangle QQQ. The length of AB´ = ´BC= ´AC
ii.
Types of triangles by the measure of their interior angles
RRR. Triangles can be classified according to the measure of their interior angels. The three types of triangles are as follows:
1. Acute triangle
WWW. XXX. 2. Right Triangle
YYY. A right triangle is a triangle in which one of its interior angles is an angle is a right angle. ∆ PQR in figure 6 is a right triangle. ∠Q is a right angle.
ZZZ.
AAAA. Figure 6. Right Triangle 3. Obtuse triangle
BBBB. An obtuse triangle is a triangle in which one of its interior angles is an obtuse triangle (The angle of magnitude between 90° and 180° .
∆ PQR in figure 7 is an obtuse triangle. ∠P is an obtuse angle. CCCC. Figure 7. Obetuse Triangle
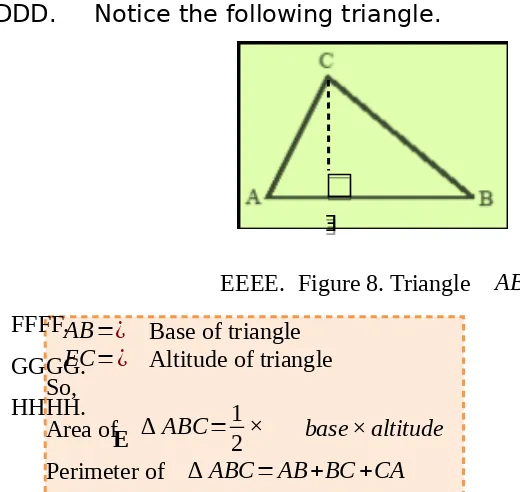
DDDD. Notice the following triangle.
EEEE. Figure 8. Triangle ABC FFFF. EC=¿ Altitude of triangle So,
Area of ∆ ABC=1
2× base× altitude Perimeter of ∆ ABC=AB+BC+CA
IIII. JJJJ.
b. Rectangular
KKKK. A rectangular is a polygon with four sides and four vertices. Consider the following picture.
LLLL. Figure 9. Rectangular
MMMM. Figure 9 is rectangular because all the flat wake that is in the picture has 4 pieces of line segment (side) and 4 corner points. Thus, based on the picture can be seen that the rectangle is divided into 6 types, namely square, rectangle, parallelograms, trapezium, rhombus, and kites.
i. Squares
NNNN.Squares is a plane ractangular whose all four interior angles are right angles and whose four sides are equal in length. In figure 10 is a Squares.
OOOO. Figure 10. Squares ABCD
PPPP. The properties of Squares:
Has two pairs of parallel sides and equal length
AB∥CD∧AD∥BC .
The length of each side of any is aqual (AB = BC = CD = DA).
Four interior angles are right angles ∠A=∠B=∠C=∠D is 90° (right angles).
QQQQ. Formula of perimeter square ¿s+s+s+s
RRRR. ¿4s
SSSS. Formula of area square ¿s × s
TTTT. ¿s2
UUUU. Note: s=¿ square side length ii. Rectangle
VVVV. A rectangle is a plane with all four angles is a right angle and opposite sides of the same length. In figure 11 is a rectangle.
WWWW. Figure 11. Rectangle ABCD
XXXX. The properties of a rectangle
Has four sides and four angles points
Has two pairs of parallel sides facing and equal length:
AD∥BC∧AB∥CD ; AD=BC∧AB=CD
The four angles are equal ∠A=∠B=∠C=∠D is 90° (right angle)
Has two equal length diagonals
Has two rotary symmetry
YYYY.Formula of perimeter rectangle ¿p+l+p+l
ZZZZ. ¿2p+2l
AAAAA. ¿2(p+l)
BBBBB. Formula of area rectangle ¿p × l CCCCC. Note: p=¿ rectangle side length
DDDDD. l=¿ rectangle side wide iii. Parallelograms
EEEEE. Jajar genjang is a plane rectangular having sides facing equal length and parallel, having two pairs of angles each of which is equal to the angle in front of it, the number of adjacent angles 180° and the two diagonals intersecting in the middle of the plane. Figure 12 is a parallelogram.
FFFFF. Figure 12. parallelograms ABCD
GGGGG. The Properties of parallelograms
Has four sides and four angles points
Has two pairs of sides that are parallel and equal in length
Has two obtuse angles and two acute angles
The opposite angle is equal
The diagonal is not the equal length
IIIII.Perimeter = Sum of all length sied ( ´
AB+ ´BC+ ´CD+ ´DA )
Area = base × altitude
iv. Trapezium
JJJJJ. The trapezium is a plane rectangular that has a pair of parallel sides, facing but not equal. Figure 13 is a trapezium.
KKKKK. Figure 13. Trapezium ABCD LLLLL. The properties of the trapezium
Has four sides and four angles points
Has a pair of sides that are parallel but not equal in lenght.
MMMMM. Formula of trapezium
NNNNN. Perimeter = The sum of all the lengths of
the sides
OOOOO. Area =
1
2(lenght side AB+lenght side AD)× altitude
v. Rhombus
PPPPP.A rhombus is a parallelogram of equal sides whose lengths are equal
and diagonally intersect perpendicular to each other. Figure 14 is a rhombus.
RRRRR. Figure 14. Rhombus ABCD SSSSS. The properties of a rhombus
Has four sides and four angles points
The four sides are the equal length
Two pairs of opposite angles are the equal
The diagonal intersects perpendicularly
Has two folding symmetry
TTTTT. Formula of rhombus
UUUUU. Perimeter ¿ The sum of all the lengths of the
sides
VVVVV. Area ¿1
2x diagonal1x diagonal2
vi. Kites
WWWWW. Kite is a plane designated by two different sides whose sides are equal in length, the opposite angle is equally large, one of the two-dimensional diagonals on two equal and vertical sides of the diagonal. Figure 15 is a kite.
XXXXX. Figure 15. Kites ABCD
YYYYY. The properties kites
Has four sides and four angles points
Has two equal angles
The diagonal intersects perpendicularly
One diagonally divides the other diagonally equally long
Has one-fold symmetry
ZZZZZ. Formula of kites
AAAAAA. Perimeter = The sum of all the lengths of the
sides
BBBBBB. Area ¿1
2×diagonal1×diagonal2 CCCCCC.
DDDDDD. Relevant Research
EEEEEE. The results of relevant research are as follows: The first study conducted by Siti Rokhimah (2015) with the title “Analisis Kesalahan Siswa dalam Menyelesaikan Soal Cerita Matematika Materi Aritmatika
error for the lower group is not reading the problem carefully and not understanding the overall meaning of the problem well.
GGGGGG. Fremework
HHHHHH. Word problem is one of the tests that are quite complicated to be done by students which resulted in most students having difficulty in understanding and solving the word problems. This is because the word problem is presented in the form of a series of sentences relating to daily life and in the process of processing requires more skills. So that students in solving the word problem of math sometimes still make mistakes, especially in aspects of geometry that students often encounter in everyday life. The student's mistakes can be influenced by several things such as, students do not understand the material well, do not understand the intent of the problem, the use of the definition or the theorem that is not appropriate, less thorough, and most importantly students still less practice to do the word problem and the causes others. Therefore it is necessary to conduct an in-depth analysis of why students make mistakes and what causes them.
writing of the answer or the student is wrong in summing up the final result.
JJJJJJ. Errors that are often done by students based on the description above can be categorized types of errors as follows: the first mistakes of students sometimes wrong in reading and understanding the problem, this can be categorized as a type of reading error. Both students already understand the problem but have not captured the important information contained in the matter so that students do not know what is asked and what is known from the problem, this can be categorized as a mistake in understanding the problem. The three students have difficulty in changing the word problem into the mathematical model, and the students are wrong in determining the problem-solving strategy, this can be categorized as a mistake in transformation. The four students are wrong in performing the counting operation, this can be categorized as a type of error in process skills. The five students are wrong in the phrase of writing answers or students wrong in summing up the final result, this can be categorized as an error in writing the final answer.
A. Type of research
B. The type of research used in this study using descriptive qualitative research type. Bogdan and Taylor (in Moleong in Darmadi, 2014: 287) suggest that qualitative research is a study that yields descriptive data in the form of written and oral words of observed persons and behaviors. Sudjana and Ibrahim (2014) mentioned that the data obtained from descriptive qualitative research are observations, interviews, photographs, written excerpts from documents, field notes, and not in the form and number of statistics. The results of the analysis of descriptive qualitative research in the form of description of the situation studied in the form of narrative descriptions.
C. Research Subject
D. This research will be conducted in Junior High School 1 Barebbo year 2017/2018 with a subject of research is a student of class VIII. Students who are subjected to research are students who have studied geometry material. Furthermore, each category of students' mathematics ability is selected by two students, where the selected students are students who have good communication skills. The categorization of students' mathematical abilities refers to the following set of ratings (Ratumanan and Laurens in Ma'sum in Maryam, 2016: 76).
1. Students are capable of higher mathematics 80≤ score is obtained ≤100 .
2. Students are capable of medium mathematics 60≤ score is obtained
¿80 .
T. Research Procedures
E. The first step in this study is the provision of tests to students who aim to classify students' math skills in high, medium, and low categories. Furthermore, each category of students' mathematics ability is selected by two students, where the selected students are students who have good communication skills. Then provide a diagnostic test of the word problem to identify mistakes made by students. In the next stage, researchers conducted interviews with students with the aim of knowing the cause of student error in solving the problem. From the causes of such errors, it can be classified errors that he did including what kind of error based on Newman's procedures. By knowing the cause of student error is expected for subsequent learning the number of students who experience difficulty will be reduced so that mistakes can be minimized and simultaneously improve the ability of students’ absorption in solving the mathematical problems of geometric matter.
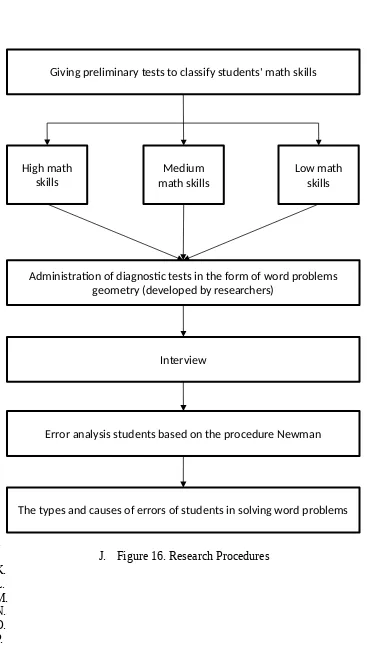
F. Based on the description above, research procedures in this study can be described as follows:
I.
J. Figure 16. Research Procedures K.
L. M. N. O. P.
Giving preliminary tests to classify students' math skills
High math skills
Administration of diagnostic tests in the form of word problems geometry (developed by researchers)
Interview Medium
math skills Low math skills
Error analysis students based on the procedure Newman
Q.
U. Research Instrument
R. This study uses several instruments. Among others: 1. Researcher as the main instrument
S. Researchers themselves as the main instrument that plays a role in data collection, interviews with respondents and analyzes the results obtained.
2. Test
T. In addition, researchers also used the test instrument. A test instrument is a tool used in the framework of measurement and assessment (Lestari and Yudhanegara, 2017: 164). The test referred to in this study is a diagnostic test. The test used in the form of a description that requires an answer to the discussion or description of words, so it can reflect the mindset of students who do it. This test is structured to collect data in writing about the type and form of student error. The test sheet is a about geometry prepared to know the type of student error in solving the problem.
3. Interview
the outline of the problem to be asked. In semi-structured interview questions can develop depending on the answers given by the subject under study.
V. Data Analysis Techniques
V. According to Patton (in Moleong, 2002), analyzing the data is the process of organizing and sorting data into patterns, categories, and units of basic descriptions so that the theme can be found and can be formulated hypotheses of work suggested by the data. The process of qualitative data analysis activities in this research is done with the following stages:
1. Data Reduction
W. Reduce data means to summarize, select the main points, focus on the things that are important, sought the theme and pattern so that the data obtained provide a clear picture and make it easier for researchers to continue collecting the next data.
X. The reduction phases in this study are.
a. Correcting student work results, then ranking to determine the students who will be the subject of research
b. The result of the students' work in solving the word problem which is the subject of the research is the raw data that must be transformed in the note as material for the interview.
c. The result of the interview is simplified into a good and neat arrangement of language, then transformed into a note.
the essentials, focusing on the things that matter, looking for the theme and pattern. Thus the data to be reduced gives a clearer picture and makes it easier for researchers to collect the next data, and look for it when necessary.
8. Presenting data
Z. The presentation of data includes the classification and identification of data, ie write a collection of valid data organized and categorized so as to enable to draw conclusions from the data.
AA. The stages of data presented in this study are:
a. Presenting the results of the interview selected students as research subjects to be interviewed.
b. Presents the results of recorded interviews. 9. Verify
BB. Verification or drawing a conclusion is part of an activity in answering questions and research objectives. a conclusion is considered credible if supported by valid and consistent evidence when the researcher fielded the data. This can be obtained by comparing the analysis of the results of work and interview students who became the subject of research so that it can be known the cause and type of student error in solving the problem of mathematical stories on the material geometry.
W. Quality Standard of Qualitative Research
test of data in qualitative research includes the test of transferability, dependability, confirmability, and credibility.
1. Transferability test
DD. The test of transferability or in quantitative research is referred to as an external validity test. External validity aims to show the degree of accuracy or the results of a study can be applied to the population where the sample is taken. And to ensure the results of such research can be applied to other contexts and social situations.
EE.To convince the reader or another researcher to understand the results of qualitative research so that there is a possibility to apply them, the researcher in making the report must provide a detailed, clear, systematic, and reliable description. Faisal (in Sugiono, 2017: 377) if the reader gets a clear picture of what "research" research report is in effect, the research report meets the standard of transferability. This is why the writer of a research report cannot guarantee this.
2. Dependability test
of researchers to show or have "trace of field activity" it can be doubted dependability of research.
3. Confirmability test
GG. Test confirmability or in quantitative research can be called objectivity test research. Sugiono (2017: 377) states that a study is said to have met the confirmability test standards if the results of the study have been agreed upon by many people. The confirmability test is almost similar to the dependability test. In this study, the confirmability test is supplemented by evidence in the form of interview recordings and test results.
4. Credibility test
HH. A research data is said to meet the test credibility (degree of confidence) if the results obtained in accordance with the facts that occurred in the field. In this study, to obtain data that can be trusted or credible then triangulation is done. According to Moleong (2007: 330) triangulation is a technique of checking the validity of data that utilizes other data outside existing data. These data to compare with existing data so as to reduce bias. According to Sugiyono (2017: 373), there are 3 types of triangulation ie triangulation of sources, triangulation techniques, and triangulation time. In this research triangulation used is triangulation technique. Triangulation technique is to check the data to the same source with different methods. The method in question is a written test method by interview method. If both methods produce the same data then the study meets the credibility test.
LL. Celements, M. (1980). Analyzing Children's Errors on Written Mathematical Tasks. Educational Studies in Mathematics.
MM. Celements, M., & ellerton, N. (1992). Implications of Newman Researh for The Issue of "What is Basic School Mathematics?".
NN. Darmadi, H. (2004). Metode Penelitian Pendidikan dan Sosial. Bandung: Alfabeta.
OO. Djadir, Minggi, I., Ja'faruddin, Zaki, A., & Sidjana, S. (2017). Sumber Belajar Penunjang PLPG 2017 Mata Pelajaran/Paket Keahlian Matematika. Makassar: Kementrian Pendidikan dan Kebudayaan Direktorat Jendral Guru dan Tenaga Kependidikan.
PP. Ekayanti, A. (2017). Diagnosis of Students' Misconception in The Evindence Process Based on Newman Error Analysis.
QQ. Hadar, N. M. (1987). An Empirical Classification Model for Errors in High School Mathematics.
RR. Haryono, & Didi. (2014). Filsafat Matematika (Suatu Tinjauan Epistomologi dan Filosofis). Bandung: Alfabeta.
SS. Iswadji, D. (2001). Geometri Ruang. Yogyakarta: JICA Universitas Negeri Yogyakarta.
TT. Lestari, K. E., & Yudhanegara, M. R. (2017). Penelitian Pendidikan Matematika. Bandung: PT.Refika Aditama.
UU. Maryam, S. (2016). Representasi Siswa SMP Dalam Menyelesaikan Soal Open-Ended Ditinjau Dari Kemampuan Matematika. Jurnal Ilmiah Pendidikan Matematika.
VV. Matematika SMP/MTs Kelas VII Semester 2, edisi revisi. (2014). Jakarta: Kementrian Pendidikan dan Kebudayaan.
WW. Moeharti. (1986). Sistem-sistem Geometri. Jakarta: Karunia Universitas Terbuka.
ZZ. NCTM. (2000). Princioles and Standards for School Mathematics. Reston Virginia: The National Council of Teachers of Matgematics, Inc.
AAA. Padmavthy, R. (2015). Influnce of Selected Demographic Factor on Mathematics Concept Error.
BBB. Prasetio, E. K. (2012, November Rabu). Blog. Retrieved from Mathematical Thingking: http://eko-kurniawan-prasetio.blogspot.co.id/2012/11/
CCC. Rasyid, S. (2000). Matematika I. Makassar: Yayasan Venus PIP Makassar.
Teori Van Hiele. Didaktik Matematika.
FFF. Singh, P., Rahman, A. A., & Hoon, T. S. (2010). The Newman Procedure For Analyzing Primary Four Pupils Errors on Written Mathematics Task: A Malaysian Perspective. Procedia Social and Behavioral Sciences.
GGG. Sudjana, N., & Ibrahim. (2014). Penelitian dan Penilaian Pendidikan. Bandung: Sinar Baru Algensido.
HHH. Sugiono. (2007). Metode Penelitian Kuantitatif Kualitatif dan R&D. Bandung: Alfabate.
III. Sugiono. (2017). Metode Penelitian Pendidikan. Bandung: AlfaBeta. JJJ. Tim Geometri. (2014). Gemetri Dasar. Makassar.
KKK. Tim Penyusun Kamus Pusat Bahasa. (2008). Kamus Bahasa Indonesia. Jakarta: Pusat Bahasa Departemen Pendidikan Nasional.
LLL. TIMSS. (2011). Countries Participating in TIMSS 2011 and in Earlier TIMSS Assessments.
MMM.Tiro, M. A. (2010). Cara Efektif Belajar Matematika. Makassar: Andira Publisher.
NNN. Walle, V. D., & Jhin, A. (2008). Matematika Sekolah Dasar dan Menengeh. Jakarta: Erlangga.
OOO. White, A. L. (2010). Numeracy, Literacy and Newman’s Error Analysis. Allan Leslie White Journal of Science and Mathematics.
PPP. Wriaatmadja, R. (2007). Metode Penelitian Tindakan Kelas. Bandung: PT.Remaja Rosdakarya.