MODEL REGRESI TERBOBOTI GEOGRAFIS BAYES UNTUK DATA KEMISKINAN (Kasus 35 Desa atau Kelurahan di Kabupaten Jember) YUSNITA

MODEL REGRESI TERBOBOTI GEOGRAFIS BAYES

UNTUK DATA KEMISKINAN

(Kasus 35 Desa atau Kelurahan di Kabupaten Jember)

YUSNITA

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2012

PERNYATAAN MENGENAI TESIS

DAN SUMBER INFORMASI

Dengan ini saya menyatakaan bahwa tesis Model Regresi Terboboti Geografis

Bayes untuk Data Kemiskinan (Kasus 35 Desa atau Kelurahan di Kabupaten

Jember) adalah karya saya dengan arahan dari komisi pembimbing dan belum

diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber

informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak

diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam

Daftar Pustaka di bagian akhir tesis ini.

Bogor, Juli 2012

Yusnita

NIM G151090141

ABSTRACT

YUSNITA. Bayesian Geographically Weighted Regression Model for Poverty

Data (Case of 35 Villages in Jember Regency). Supervised by AJI HAMIM

WIGENA and ANIK DJURAIDAH.

Bayesian Geographically Weighted Regression (BGWR) is locally linear

regression method to solve some difficulties that arise in Geographically

Weighted Regression (GWR) model, such as outliers or non-constant variance.

The Bayesian approach solves the problems by producing estimates that are robust

against aberrant observations. The aberrant observations are automatically

detected and downweighted to mitigate their influence on the estimates. In this

research, the weighting used for BGWR model is Gaussian and bi-square kernel

function. The results showed that BGWR model is better than GWR model.

According to mean square error (MSE) values and coefficient of determinant (R

2

),

Gaussian kernel function is better than bi-square kernel function as BGWR

weighting to analyze the data on average expenditure per capita of 35 villages in

Jember Regency.

Keywords: Bayesian, Geographically Weighted Regression, outlier, non-constant

variance, Gaussian kernel, bi-square kernel

RINGKASAN

YUSNITA. Model Regresi Terboboti Geografis Bayes untuk Data Kemiskinan

(Kasus 35 Desa atau Kelurahan di Kabupaten Jember). Dibimbing oleh AJI

HAMIM WIGENA dan ANIK DJURAIDAH.

Permasalahan kemiskinan penduduk di Indonesia masih cukup serius.

Berbagai upaya telah dilakukan oleh pemerintah untuk menanggulangi masalah

ini, diantaranya dengan memprediksi wilayah-wilayah miskin hingga tingkat

administrasi desa, sehingga diharapkan upaya pengentasan kemiskinan lebih tepat

sasaran. Data yang biasanya digunakan dalam menentukan suatu wilayah desa

tergolong miskin atau tidak adalah rata-rata pengeluaran rumah tangga per kapita.

Analisis untuk menentukan miskin tidaknya suatu desa, umumnya masih

menggunakan analisis yang masih bersifat global dan diberlakukan pada seluruh

lokasi yang diamati. Namun kondisi data di lokasi yang satu dengan lokasi yang

lain tidak sama, baik dari segi geografis, keadaan sosial-budaya maupun hal-hal

lain yang melatarbelakanginya, sehingga muncul keragaman antar wilayah lokal

atau heterogenitas spatial. Salah satu dampak yang ditimbulkan dari munculnya

heterogenitas spasial adalah parameter regresi

bervariasi secara spasial. Selain itu,

masalah kemiskinan dan kondisi ketertinggalan suatu desa sangat mungkin

dipengaruhi oleh lokasi pengamatan atau kondisi geografis desa, termasuk

posisinya terhadap desa lain disekitarnya. Hal ini dipertegas dengan hukum

pertama geografi yang dikemukakan Tobler (1979) yang menyatakan bahwa

segala sesuatu saling berhubungan satu dengan yang lainnya, tetapi sesuatu yang

lebih dekat akan lebih berpengaruh daripada sesuatu yang jauh.

Efek spasial

menyebabkan asumsi kebebasan antar pengamatan yang diperlukan dalam regresi

global sulit dipenuhi. Untuk mengakomodir permasalahan tersebut, analisis

Regresi Terboboti Geografis (RTG) atau Geographically Weighted Regression

adalah salah satu solusi yang dapat digunakan untuk membentuk model regresi

yang bersifat lokal untuk setiap lokasi.

Isu penting dalam model RTG adalah masalah pencilan atau ragam tidak

konstan antar amatan. Koefisien regresi yang berbeda-beda di tiap lokasi

pengamatan memungkinkan ragam galat yang berbeda-beda pula untuk tiap lokasi

pengamatan, sehingga salah satu solusi dari permasalahan tersebut adalah

pendekatan Bayes yang disebut Regresi Terboboti Geografis Bayes (RTGB) atau

Bayesian Geographically Weighted Regression. Model RTGB mengasumsikan

ragam galat tidak konstan antar lokasi amatan, sehingga dapat mengakomodir

adanya permasalahan keheterogenan ragam. Pendekatan Bayes secara langsung

mendeteksi dan memboboti pengamatan yang berpotensi mengandung pencilan,

sehingga dapat mengurangi efek pencilan terhadap pendugaan parameter model.

Pendugaan parameter model RTGB menggunakan Gibbs sampling yaitu suatu

teknik yang digunakan untuk membangkitkan contoh acak dari distribusi

berdasarkan pendekatan Markov Chain Monte Carlo (MCMC). Pembobot yang

digunakan adalah fungsi kernel normal (Gaussian) dan fungsi kernel kuadrat

ganda (bi-square).

Hasil analisis menunjukkan bahwa berdasarkan nilai KTG dan R

2

yang

digunakan sebagai indikator kebaikan model, model RTGB lebih baik daripada

model RTG dalam menjelaskan peubah jarak dari desa atau kelurahan ke ibukota

kabupaten atau kota (km), banyaknya sarana kesehatan di desa (poskesdes,

polindes, posyandu, apotek dan toko khusus obat) per 1000 penduduk, dan

persentase keluarga penerima ASKESKIN dalam setahun terakhir terhadap

rata-rata pengeluaran per kapita per bulan penduduk desa atau kelurahan di Kabupaten

Jember. Pada penelitian ini, fungsi pembobot kernel normal lebih baik daripada

fungsi pembobot kernel kuadrat ganda sebagai pembobot model RTGB untuk

analisis data kemiskinan di 35 desa atau kelurahan di Kabupaten Jember.

Kata kunci : Bayes, Regresi Terboboti Geografis, pencilan, ragam tidak konstan,

Gibbs sampling, kernel normal, kernel kuadrat ganda

© Hak Cipta milik IPB, tahun 2012

Hak Cipta dilindungi Undang-undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan

atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan,

penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik,

atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan

kepentingan yang wajar bagi IPB

Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis

dalam bentuk apa pun tanpa izin IPB

MODEL REGRESI TERBOBOTI GEOGRAFIS BAYES

UNTUK DATA KEMISKINAN

(Kasus 35 Desa atau Kelurahan di Kabupaten Jember)

YUSNITA

Tesis

Sebagai salah satu syarat untuk memperoleh gelar

Magister Sains pada

Program Studi Statistika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2012

Judul Tesis

: Model Regresi Terboboti Geografis Bayes untuk Data

Kemiskinan (Kasus 35 Desa atau Kelurahan di Kabupaten

Jember)

Nama

: Yusnita

NRP

: G151090141

Program Studi

: Statistika

Disetujui

Komisi Pembimbing

Dr. Ir. Aji Hamim Wigena, M.Sc.

Ketua

Dr. Ir. Anik Djuraidah, MS

Anggota

Diketahui,

Ketua Program Studi Statistika

Dr. Ir. Erfiani, M.Si.

Dekan Sekolah Pascasarjana

Dr. Ir. Dahrul Syah, M.Sc.Agr

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat

dan karunia-Nya sehingga karya ilmiah ini dapat diselesaikan. Judul tesis ini

adalah “Model Regresi Terboboti Geografis Bayes untuk Data Kemiskinan (Kasus

35 Desa atau Kelurahan di Kabupaten Jember)”.

Terima kasih penulis sampaikan kepada Bapak Dr. Ir. Aji Hamim Wigena,

M.Sc selaku pembimbing I dan Ibu Dr. Ir. Anik Djuraidah, MS selaku

pembimbing II, terima kasih atas bimbingan, saran dan waktunya. Disamping itu

penulis juga mengucapkan terima kasih kepada bapak Dr. Anang Kurnia selaku

penguji luar komisi pada ujian tesis. Terimakasih juga penulis sampaikan kepada

seluruh staf Program Studi Statistika.

Penulis juga ingin menyampaikan penghargaan dan terima kasih kepada

keluarga, terutama kedua orangtua saya tercinta dan kakak-kakakku atas do‟a,

dukungan dan dorongan semangat, serta kasih sayangnya tanpa henti. Terima

kasih pula kepada teman-teman Statistika dan Statistika Terapan atas bantuan dan

kebersamaannya. Semoga karya ilmiah ini dapat bermanfaat.

Bogor, Juli 2012

RIWAYAT HIDUP

Penulis dilahirkan di Buton, Sulawesi Tenggara pada tanggal 1 November

1986 dari pasangan Bapak H. Nur Salim dan Ibu Hj. Siti Rukaya. Penulis

menyelesaikan pendidikan SLTA di SMAN 2 Bau-Bau pada tahun 2004 dan pada

tahun yang sama melanjutkan perkuliahan di Program Studi Statistika Terapan

Fakultas Sains Terapan Institut Sains dan Teknologi AKPRIND Yogyakarta dan

selesai pada tahun 2009. Tahun 2009 penulis diterima di Program Studi Statistika

pada Sekolah Pascasarjana IPB.

DAFTAR ISI

Halaman

DAFTAR TABEL………..

DAFTAR GAMBAR……….

DAFTAR LAMPIRAN………..

PENDAHULUAN

Latar Belakang………...

Tujuan Penelitian………...

TINJAUAN PUSTAKA

Model RTGB……….

Pendugaan Parameter RTGB……….

Pembobot Spatial………...

Kebaikan Model RTGB……….

METODOLOGI PENELITIAN

Data………

Metode………

HASIL DAN PEMBAHASAN

Deskripsi Data………

Model RTGB………..

Model Terbaik………

Asumsi Normalitas……….

KESIMPULAN DAN SARAN

Kesimpulan………

Saran………..

DAFTAR PUSTAKA……….

LAMPIRAN……….

xiii

xiv

xv

1

3

5

7

9

9

11

12

15

16

21

25

27

27

29

31

DAFTAR TABEL

Halaman

1 Statistik deskriptif peubah penjelas…...………...

2 Korelasi Pearson antar peubah………..

3 Nilai R

2

dan KTG untuk model RTGB dengan fungsi

pembobot kernel normal………...

4 Nilai R

2

dan KTG untuk model RTGB dengan fungsi

pembobot kernel kuadrat ganda……….

5 Nilai R

2

dan KTG untuk model RTG dan RTGB dengan

pembobot kernel normal dan pembobot kernel kuadrat ganda …...………..

15

16

22

22

23

DAFTAR GAMBAR

Halaman

1 Peta Kabupaten Jember……...……….

2 Plot koefisien 𝜷

₁

model RTG dan RTGB kernel normal

pada r = 35 dan



= 10…….………

3 Plot koefisien 𝜷

₁

model RTG dan RTGB kernel kuadrat ganda

pada r = 35 dan



= 10…….………

4 Plot koefisien 𝜷

2

model RTG dan RTGB kernel normal

pada r = 35 dan



= 10…….………

5 Plot koefisien 𝜷

2

model RTG dan RTGB kernel kuadrat ganda

pada r = 35 dan



= 10…….………

6 Plot koefisien 𝜷

3

model RTG dan RTGB kernel normal

pada r = 35 dan



= 10…….………

7 Plot koefisien 𝜷

₃

model RTG dan RTGB kernel kuadrat ganda

pada r = 35 dan



= 10…….………

8 Nilai 𝑽

𝑖

pada model RTGB pembobot kernel normal

dan RTGB pembobot kernel kuadrat ganda……..………..

9 Diagram pencar Y amatan dan Y duga: Regresi, RTG dan RTGB

pembobot kernel normal dan kernel kuadrat ganda……..………..

10 Plot peluang galat RTGB pembobot kernel normal……...….………

11 Plot peluang galat RTGB pembobot kernel kuadrat ganda ……..…..……

11

17

17

18

19

19

20

21

24

25

25

DAFTAR LAMPIRAN

Halaman

1 Penduga parameter model RTGB kernel normal………..

2 Penduga parameter model RTGB kernel kuadrat ganda……….…………..

3 Nilai 𝑉

_𝑖

model RTGB kernel normal ……..………..

4 Nilai 𝑉

_𝑖

model RTGB kernel kuadrat ganda ……….………

5 Program RTGB……….……….

33

45

57

60

63

PENDAHULUAN

Latar Belakang

Menurut Badan Pusat Statistik (BPS 2011), penduduk miskin adalah

penduduk yang memiliki rata-rata pengeluaran per kapita per bulan di bawah garis

kemiskinan. Garis kemiskinan dipergunakan sebagai batas untuk menentukan

miskin atau tidaknya seseorang. Pada periode Maret 2011, garis kemiskinan

sebesar Rp. 233.740,- per kapita per bulan. Dengan memperhatikan garis

kemiskinan, berdasarkan survei BPS tahun 2011, jumlah orang miskin di

Indonesia sebesar 30,02 juta jiwa atau 12,49 persen dari total jumlah penduduk.

Hal ini menunjukkan bahwa permasalahan kemiskinan penduduk di Indonesia

cukup serius. Berbagai upaya telah dilakukan oleh pemerintah untuk

menanggulangi masalah ini, di antaranya dengan memprediksi wilayah-wilayah

miskin hingga tingkat administrasi desa, sehingga dengan adanya informasi

sampai tingkat wilayah desa ini diharapkan upaya pengentasan kemiskinan lebih

tepat sasaran (BPS 2005).

BPS menggunakan rata-rata pengeluaran rumah tangga per kapita sebagai

indikator utamanya dalam mengukur kemiskinan. Analisis mengenai kemiskinan

yang umum digunakan adalah analisis yang masih bersifat global dan

diberlakukan pada seluruh lokasi yang diamati, di antaranya analisis regresi.

Pendekatan model global ini berarti menggunakan rata-rata dari wilayah-wilayah

yang lebih kecil (wilayah lokal) ditempat tersebut. Namun kondisi data di lokasi

yang satu dengan lokasi yang lain tidak sama, baik dari segi geografis, keadaan

sosial-budaya maupun hal-hal lain yang melatarbelakanginya, sehingga muncul

heterogenitas spatial. Pendekatan model global akan memberikan informasi yang

andal untuk wilayah lokal jika tidak ada atau hanya ada sedikit keragaman antar

wilayah lokalnya (Fotheringham et al. 2002).

Salah satu dampak yang ditimbulkan dari munculnya heterogenitas spasial

adalah parameter regresi

bervariasi secara spasial

.

Jika terjadi heterogenitas spasial pada parameter regresi, maka informasi yang tidak dapat ditangani oleh metode regresi global akan ditampung sebagai galat. Bila kasus semacam itu terjadi, regresi global menjadi kurang mampu dalam menjelaskan fenomena data yang sebenarnya.

Salah satu asumsi yang diperlukan pada analisis regresi global adalah antar pengamatan harus bersifat saling bebas, tetapi

masalah kemiskinan dan kondisi

ketertinggalan suatu desa sangat mungkin dipengaruhi oleh lokasi pengamatan

atau kondisi geografis desa, termasuk posisinya terhadap desa lain di sekitarnya.

Hal ini dipertegas dengan hukum pertama geografi yang dikemukakan Tobler

(1979) dalam Schabenberger dan Gotway (2005) yang berbunyi ”Segala sesuatu

saling berhubungan satu dengan yang lainnya, tetapi sesuatu yang lebih dekat

akan lebih berpengaruh daripada sesuatu yang jauh”.

Efek spasial menyebabkan

asumsi kebebasan antar pengamatan yang diperlukan dalam regresi sulit dipenuhi,

sehingga dalam statistika, model yang dapat menjelaskan hubungan antara suatu

wilayah dengan wilayah di sekitarnya adalah model spatial.

Analisis Regresi Terboboti Geografis (RTG) dapat digunakan untuk

mengatasi masalah tersebut. RTG merupakan bagian dari analisis spasial yang

bersifat lokal dengan pembobotan berdasarkan posisi atau jarak dari satu lokasi

pengamatan dengan lokasi pengamatan lainnya.

Parameter regresi pada model RTG diasumsikan bervariasi secara spasial, sehingga interpretasi yang berbeda dan berharga dapat diperoleh untuk setiap titik lokasi yang diteliti.

Isu penting dalam model RTG adalah masalah pencilan atau ragam tidak

konstan antar amatan. Koefisien regresi yang berbeda di tiap lokasi pengamatan

memungkinkan ragam galat yang berbeda pula untuk tiap lokasi pengamatan.

Efek pencilan juga akan mengakibatkan masalah heteroskedastisitas. Pendekatan

Bayes dalam model RTG yang disebut Regresi Terboboti Geografis Bayes

(RTGB) atau Bayesian Geographically Weighted Regression yang diperkenalkan

LeSage adalah analisis yang tepat untuk menangani permasalahan tersebut.

Pendekatan ini secara langsung mendeteksi dan memboboti pengamatan yang

berpotensi mengandung pencilan, sehingga dapat mengurangi efek pencilan

terhadap pendugaan parameter model. Pendekatan Bayes mengasumsikan ragam

galat tidak konstan antar lokasi amatan, sehingga dapat mengatasi adanya

permasalahan keheterogenan ragam galat antar lokasi.

Penelitian tentang analisis spasial telah banyak dikembangkan, antara lain

Meilisa (2010) menyatakan bahwa model otoregresif bersyarat (CAR) dan model

otoregresif simultan (SAR) sama baiknya dalam menentukan faktor-faktor

kemiskinan di Provinsi Jawa Timur. Arisanti (2010) menyatakan bahwa model

otoregresif lag spasial lebih baik dalam menentukan faktor-faktor yang

berpengaruh terhadap kemiskinan di Provinsi Jawa Timur dibandingkan regresi

linier klasik. Khusus untuk penelitian tentang RTG telah dilakukan oleh

Rahmawati (2010) yang meneliti tentang model Regresi Terboboti Geografis

(RTG) dengan pembobot kernel normal dan kernel kuadrat ganda untuk data

kemiskinan pada desa atau kelurahan di Kabupaten Jember. Hasil penelitiannya

diperoleh bahwa model RTG dengan pembobot kernel normal lebih baik

digunakan untuk memodelkan rata-rata pengeluaran per kapita per bulan desa atau

kelurahan dengan peubah-peubah penjelasnya, dibandingkan dengan model RTG

dengan pembobot kernel kuadrat ganda dan model regresi klasik.

Pembobot yang digunakan pada penelitian ini adalah pembobot jarak yang

juga digunakan pada penelitian Rahmawati (2010), yaitu pembobot kernel normal

(Gaussian) dan pembobot kernel kuadrat ganda (bi-square), sehingga diharapkan

dapat membandingkan dan menentukan model terbaik antara RTG dan RTGB

dengan pembobot kernel normal dan kernel kuadrat ganda pada kasus 35 desa

atau kelurahan di Kabupaten Jember. Kabupaten Jember dipilih sebagai studi

kasus pada penelitian ini karena berdasarkan data survei sosial ekonomi nasional

(Susenas) Maret 2009, dari 38 kabupaten/kota di Jawa Timur, jumlah masyarakat

miskin yang tertinggi yakni Kabupaten Jember yang mencapai 237.700 rumah

tangga.

Tujuan

Tujuan penelitian ini dapat dirumuskan sebagai berikut:

1. Membentuk model RTGB dengan fungsi pembobot kernel normal dan kernel

kuadrat ganda untuk pendugaan rata-rata pengeluaran per kapita per bulan

desa atau kelurahan.

TINJAUAN PUSTAKA

Model RTGB

Analisis regresi merupakan analisis statistika yang bertujuan untuk

memodelkan hubungan antara peubah respon Y dengan peubah penjelas X, di

mana dugaan parameter persamaan berlaku untuk semua lokasi pengamatan.

Model RTG merupakan pengembangan dari model regresi, tapi pada model RTG

parameter persamaan untuk setiap lokasi pengamatan berbeda dengan lokasi

lainnya, sehingga banyaknya vektor parameter yang diduga sama dengan

banyaknya lokasi pengamatan yang digunakan dalam data. Model yang dihasilkan

pada analisis RTG juga tidak dapat digunakan untuk menduga parameter selain

parameter di lokasi pengamatan (Walter et al. 2005). Secara umum model RTG

dapat ditulis dalam bentuk matriks berikut:

𝑾

𝑖

𝒚 = 𝑾

𝑖

𝑿𝜷

𝑖

+ 𝜺

𝑖

(1)

𝜷

𝑖

merupakan vektor parameter berukuran k



1 pada pengamatan ke-𝑖. Pendugaan

parameter model untuk setiap lokasi pengamatan dengan metode kuadrat terkecil

terboboti untuk lokasi ke-𝑖, yaitu:

𝒃

_𝑖

= (𝑿′𝑾

_𝑖

𝑿)

−1

_𝑿′𝑾

𝑖

𝒚

(2)

dengan

𝑾

_𝑖

= 𝑑𝑖𝑎𝑔[𝑤

_𝑖1

, 𝑤

_𝑖2

, … , 𝑤

_𝑖𝑛

] dan 0 ≤ 𝑤

_𝑖𝑗

≤ 1 (𝑖, 𝑗 = 1, 2, …, n)

𝑾

_𝑖

adalah matriks diagonal berukuran n



n (n = banyaknya pengamatan) yang

merupakan matriks pembobot spasial lokasi ke-𝑖 (spatial weighting). Unsur-unsur

diagonal matriks

𝑾

𝑖

diambil dari vektor baris atau kolom ke-𝑖 dari matriks

pembobot W. Nilai unsur-unsur diagonal

𝑾

_𝑖

ditentukan oleh kedekatan

pengamatan (lokasi) ke-𝑖 dengan lokasi lainnya (lokasi ke-𝑗). Semakin dekat

lokasinya, semakin besar nilai pembobot pada unsur yang bersesuaian.

Ragam galat pada model RTG diasumsikan homogen, sehingga tidak dapat

menyelesaikan masalah yang muncul akibat adanya ragam yang tidak konstan

antar area atau pencilan. LeSage (1998) menyelesaikan permasalahan tersebut

dengan menggunakan pendekatan Bayes. Model RTG pada persamaan (1)

dikembangkan dengan memasukan parameter penghalus hubungan atau

parameter smoothing relationship berikut:

𝜷

_𝑖

= 𝑤

_𝑖1

⊗ 𝑰

_𝑘

… 𝑤

_𝑖𝑛

⊗ 𝑰

_𝑘

𝜷

1

⋮

𝜷

𝑛

+ 𝒖

_𝑖

(3)

𝑤

_𝑖𝑗

merupakan pembobot jarak antara lokasi ke-𝑖 dengan lokasi lainnya (lokasi

ke-𝑗) yang dinormalkan sehingga jumlah vektor baris (𝑤

𝑖1

,

𝑤

𝑖2

, …, 𝑤

𝑖𝑛

) = 1,

dengan 𝑤

_𝑖𝑖

= 0.

Sebaran galat pada persamaan (1) dan (3) sebagai berikut:

𝜺

_𝑖

~𝑁[0, 𝜎

2

_𝑽

𝑖

]

(4)

𝒖

_𝑖

~𝑁[0, 𝜎

2

_𝛿

2

_(𝑿

′

_𝑾

𝑖𝟐

𝑿)

−1

]

(5)

dengan:

𝑽

_𝑖

= 𝑑𝑖𝑎𝑔[𝑣

₁

, 𝑣

₂

, … , 𝑣

_𝑛

]

𝑟 𝑣𝑖

~ 𝜒

2 (𝑟)

𝑟

𝜎

2

adalah ragam galat dan

𝑽

𝑖

adalah matriks diagonal berukuran nxn yang

menunjukkan ragam tidak konstan antar lokasi amatan. Sebaran prior

𝑽

𝑖





2(r)

,

dimana r adalah hyperparameter yang mengontrol sejumlah sebaran pendugaan

𝑽

_𝑖

. Prior ini digunakan oleh Lindley (1971) dalam LeSage (1998) untuk analisis

masalah ragam, Geweke (1993) dalam LeSage (1998) untuk model

heteroskedastisitas dan pencilan, LeSage (1998) dalam model spatial autoregresif.

Prior ini digunakan dengan memodifikasi

𝑽

_𝑖

sehingga E(

𝑽

_𝑖

) = 1 dan Var(𝑽

_𝑖

) =

2/r, jika r menjadi sangat besar, maka ragam galat model RTGB menjadi

𝜎

2

_𝑰

𝑛

(homoskedastisitas atau ragam konstan). Nilai hyperparameter r yang kecil

mengasumsikan bahwa prior meyakini adanya ragam yang tidak konstan antar

lokasi.

Parameter stokastik 𝒖

_𝑖

pada parameter penghalus hubungan dalam

persamaan (3) menyebar normal dengan rataan nol dan ragam berdasarkan

Zellner‟s g-prior yang sebanding dengan matriks ragam-peragam, 𝜎

2

_(𝑿

′

_𝑾

𝑖𝟐

𝑿)

−1

dengan

𝛿

2

sebagai faktor skala (scale factor) yang mengatur

𝜷

𝑖

. Prior ini

digunakan untuk menunjukkan keragaman parameter penghalus hubungan

𝜷

_𝑖

(LeSage 1998). Jika

𝛿

2

→ ∞ (𝑽

_𝑖

= I

n

), maka pendugaan RTGB akan

menghasilkan pendugaan yang sama dengan RTG. LeSage menunjukkannya pada

bentuk persamaan berikut :

𝜷

_𝑖

= 𝑱

_𝑖

𝜸 + 𝒖

_𝑖

(7)

dengan:

𝒚

_𝑖

= 𝑾

_𝑖

𝒚

𝑿

_𝑖

= 𝑾

_𝑖

𝑿

𝑱

𝑖

= 𝑤

𝑖1

⊗ 𝑰

𝑘

… 𝑤

𝑖𝑛

⊗ 𝑰

𝑘

𝜸 =

𝜷

₁

⋮

𝜷

_𝑛

Persamaan (6) dan (7) dapat ditulis dalam bentuk persamaan (8).

𝒚

𝑖

𝑱

_𝑖

𝜸

=

𝑿

_𝑖

−𝑰

𝑘

𝜷

_𝑖

+

_𝒖

𝝐

𝑖 𝑖

(8)

Jika 𝑽

𝑖

= I

n

, maka 𝜷

𝑖

adalah sebagai berikut:

𝜷

_𝑖

= 𝑹(𝑿

_𝑖

′𝒚

_𝑖

+ 𝑿

_𝑖

′𝑿

_𝑖

𝑱

_𝑖

𝜸/𝛿

2

)

𝑹 = (𝑿

𝑖

′𝑿

𝒊

+ 𝑿

𝑖

′𝑿

𝑖

/𝛿

2

)

−1

dan jika

𝛿

2

_{→ ∞, maka pendugaan RTGB sama dengan pendugaan RTG yang}

ditunjukkan pada persamaan berikut:

𝜷

_𝑖

= (𝑿

_𝑖

′𝑿

_𝑖

)

−1

(𝑿

_𝑖

′𝒚

)

_𝑖

Pendugaan Parameter RTGB

LeSage (2001) menggunakan Gibbs sampling yaitu suatu teknik yang

digunakan untuk membangkitkan contoh acak dari distribusi berdasarkan

pendekatan Markov Chain Monte Carlo (MCMC) untuk mendapatkan pendugaan

parameter. Metode Gibbs sampling digunakan untuk

menemukan solusi masalah matematis (yang dapat terdiri dari banyak peubah) yang susah dipecahkan, misalnya dengan kalkulus integral, atau metode numerik lainnya. Parameter yang akan diduga

dalam proses ini adalah

𝜷

_𝑖

,

𝜎, 𝛿, 𝑽

_𝑖

dan



dengan sebaran posterior bersyarat

adalah sebagai berikut:

Sebaran posterior 𝜷

_𝑖

dengan syarat 𝜎

_𝑖

, 𝛿, 𝜸 dan 𝑽

_𝑖

adalah:

𝑝(𝜷

𝑖

| … ) ∝ 𝑁(𝜷

𝑖

, 𝜎

𝑖2

𝑹)

(9)

dengan:

𝑹 = (𝑿

𝑖

′𝑽

𝒊−𝟏

𝑿

𝒊

+ 𝑿

𝑖

′𝑿

𝑖

/𝛿

2

)

−1

Sebaran posterior bersyarat untuk σ adalah



2(m)

yang ditunjukkan pada

persamaan (10).

𝑝(𝜎

𝑖

| … ) ∝ 𝜎

𝑖− 𝑚 +1

exp⁡

{− 1 2𝜎

𝑖2

𝜺

𝑖 ′

_𝑽

𝑖−1

𝜺

𝑖

}

(10)

𝜺

_𝑖

= 𝒚

_𝑖

− 𝑿

_𝑖

𝜷

_𝑖

dengan m menunjukkan jumlah pengamatan dengan pembobot yang berarti atau

tidak bernilai nol.

Sebaran posterior bersyarat untuk 𝑽

𝑖

adalah:

𝑝{[ 𝒆

_𝑖𝟐

_𝜎

𝑖2

+ 𝑟]/𝑽

𝑖

| … } ∝ 𝜒

2_(𝑟+1)

(11)

Sebaran posterior bersyarat untuk



adalah



2(nk)

yang ditunjukkan pada

persamaan (12).

𝑝(𝛿| … ) ∝ 𝛿

−𝑛𝑘

_exp⁡

_{−

_𝜷

𝑖

− 𝑱

𝑖

𝜸

′ 𝑛

𝑖=1

(𝑿

𝑖

′𝑿

𝑖

)

−1

𝜷

𝑖

− 𝑱

𝑖

𝜸 / 2𝜎

𝑖2

𝛿

2

} (12)

Tahapan proses Gibbs sampling adalah sebagai berikut:

1. Menentukan nilai secara acak untuk parameter 𝜷

_𝑖0

, 𝜎

0

_{, 𝛿}

0

_{, 𝑽}

𝑖0

, 𝜸

0

2. Tiap observasi 𝑖 = 1,…, n,

a. Bangkitkan 𝜷

𝑖1

dari 𝑃(𝜷

𝑖

|𝜎

0

, 𝛿

0

, 𝑽

𝑖0

, 𝜸

0

) pada persamaan (9)

b. Bangkitkan 𝜎

1

_{dari 𝑃(𝜎|𝛿}

0

_{, 𝜷}

𝑖1

, 𝑽

𝑖

0

, 𝜸

0

_{) pada persamaan (10)}

c. Bangkitkan 𝑉

_𝑖1

dari 𝑃(𝑽

_𝑖

|𝜷

_𝑖1

, 𝜎

1

, 𝛿

0

, 𝜸

0

) pada persamaan (11)

3. Gunakan nilai 𝜷

_𝑖1

, 𝑖 = 1, …, n untuk memperbaharui 𝜸

0

menjadi 𝜸

1

4. Nilai 𝛿

1

diperoleh dari 𝑃(𝛿|𝜷

𝑖1

, 𝜎

1

, 𝑽

𝑖1

, 𝜸

1

) pada persamaan (12)

5. Ganti nilai 𝜷

_𝑖0

, 𝜎

0

_{, 𝛿}

0

_{, 𝑽}

𝑖0

, 𝜸

0

pada langkah 1 dengan 𝜷

𝑖1

, 𝜎

1

, 𝛿

1

, 𝑽

𝑖1

, 𝜸

1

6. Ulangi langkah 1-5 sebanyak q bangkitan hingga mendekati konvergen.

Dugaan parameter diperoleh dari rataan contoh posterior.

Pembobot Spasial

Fungsi pembobot spasial yang digunakan dalam penelitian ini sebagai

berikut:

1.

𝑤

_𝑖𝑗

=

_{𝑒𝑥𝑝 − 1 2}

𝑑

𝑖𝑗

_𝜃

2

dengan 𝑑

_𝑖𝑗

adalah jarak dari lokasi-𝑖 ke lokasi-𝑗

dan

𝜃 adalah lebar jendela, yaitu suatu nilai parameter penghalus fungsi yang

nilainya selalu positif. Fungsi ini biasa disebut fungsi kernel normal

(Gaussian).

2.

𝑤

𝑖𝑗

=

1 −

𝑑

_𝑖𝑗

𝜃

2 2

jika

𝑑

𝑖𝑗

<

𝜃, dan 𝑤

𝑖𝑗

= 0 untuk

𝑑

𝑖𝑗

≥

𝜃. fungsi ini

mengikuti bentuk kernel pembobot ganda (biweight) dan biasa disebut sebagai

fungsi pembobot kernel kuadrat ganda (bi-square).

Salah satu cara yang dapat digunakan untuk mendapatkan nilai lebar jendela

optimum yaitu dengan validasi silang (cross validation). Lebar jendela optimum

yang digunakan adalah yang menghasilkan nilai koefisien validasi silang

minimum, dengan rumus koefisiennya adalah:

𝐶𝑉 =

𝑛𝑖=1

𝑦

𝑖

− 𝑦

≠𝑖

(𝜃)

2

dengan

𝑦

_≠𝑖

(𝜃) adalah nilai dugaan

y

i

(fitting value) dengan pengamatan di lokasi

ke-𝑖 dihilangkan dari proses prediksi (Fotheringham et al. 2002). Lebar jendela

optimum diperoleh dengan proses iterasi hingga didapatkan CV minimum.

Kebaikan Model RTGB

Ukuran kebaikan model yang digunakan pada penelitian ini adalah koefisien

determinasi (R

2

) dan kuadrat tengah galat (KTG). R

2

diartikan sebagai rasio antara

jumlah kuadrat regresi (JKR) dan jumlah kuadrat total (JKT), sehingga R

2

yang

lebih tinggi mengindikasikan model yang lebih baik.

R

2

=

𝑛𝑖=1

𝑦

𝑖

− 𝑦

2 𝑛𝑖=1

𝑦

𝑖

− 𝑦

2

= JKR JKT

KTG diartikan sebagai perbedaan rata-rata jumlah kuadrat y

i

sebenarnya dan

penduganya, sehingga pendugaan yang paling akurat akan mengarah ke nilai KTG

terkecil.

METODOLOGI PENELITIAN

Data

Wilayah yang digunakan pada penelitian ini adalah 35 desa atau kelurahan

yang teramati dalam Susenas 2008 dari 248 desa atau kelurahan di Kabupaten

Jember. Kabupaten Jember merupakan bagian dari Propinsi Jawa Timur, terletak

± 200 km ke arah timur dari Surabaya. Secara geografis Kabupaten Jember

terletak pada 113,30º - 113,45º BT dan 8,00º - 8,30º LS. Wilayah Kabupaten

Jember berbatasan dengan Kabupaten Bondowoso, Kabupaten Probolinggo, dan

Kapubaten Situbondo di sebelah utara, sebelah timur berbatasan dengan

Kabupaten Lumajang dan Kabupaten Probolinggo, sebelah selatan berbatasan

dengan Samudra Hindia. Luas wilayah Kabupaten Jember adalah 3.293,34 km²

yang terbagi menjadi 31 kecamatan dan 248 desa/kelurahan, dengan jumlah

penduduk 2.168.732 jiwa yang terdiri atas laki-laki 1.054.729 jiwa dan perempuan

1.114.003 jiwa.

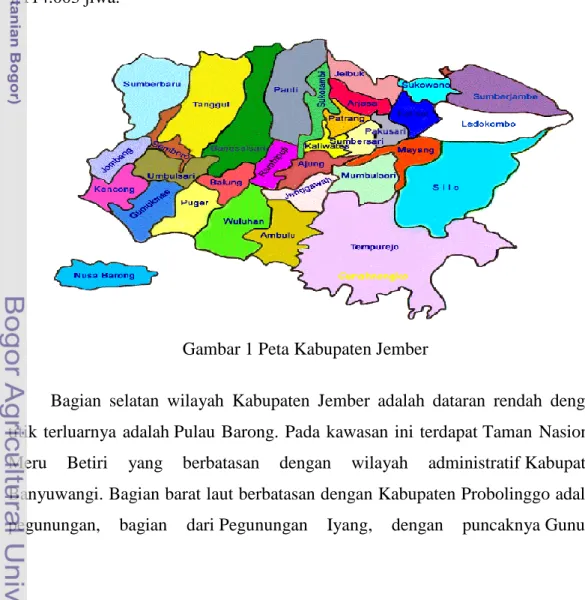
Gambar 1 Peta Kabupaten Jember

Bagian selatan wilayah Kabupaten Jember adalah dataran rendah dengan

titik terluarnya adalah Pulau Barong. Pada kawasan ini terdapat Taman Nasional

Meru Betiri yang berbatasan dengan wilayah administratif Kabupaten

Banyuwangi. Bagian barat laut berbatasan dengan Kabupaten Probolinggo adalah

pegunungan, bagian dari Pegunungan Iyang, dengan puncaknya Gunung

Argopuro (3.088 m). Bagian timur merupakan bagian dari rangkaian Dataran

Tinggi Ijen. Kabupaten Jember memiliki beberapa sungai antara lain Sungai

Bedadung yang bersumber dari Pegunungan Iyang di bagian Tengah, Sungai

Mayang yang bersumber dari Pegunungan Raung di bagian timur, dan Sungai

Bondoyudo yang bersumber dari Pegunungan Semeru di bagian barat.

Data yang digunakan dalam penelitian ini adalah data potensi desa (Podes)

dan survei sosial nasional (Susenas) tahun 2008. Peubah responnya (Y) adalah

rata-rata pengeluaran per kapita per bulan penduduk desa atau kelurahan yang

diperoleh dari data Susenas 2008. Peubah-peubah penjelas diperoleh dari data

Podes 2008 yang terdiri dari:

X

1

= Jarak dari desa atau kelurahan ke ibukota kabupaten atau kota (km),

X

2

= Banyaknya sarana kesehatan di desa atau kelurahan (poskesdes, polindes,

posyandu, apotik, dan toko obat) per 1000 penduduk (X

2

),

X

3

= Persentase keluarga penerima ASKESKIN dalam setahun terakhir (%).

Metode

Prosedur analisis yang akan dilakukan dalam penelitian ini sebagai berikut:

1. Menentukan matriks W dari jarak antar desa dan lebar jendela optimum untuk

kedua fungsi pembobot yang digunakan dalam penelitian ini.

2. Normalisasi vektor baris dari matriks W pada langkah 1 untuk kedua fungsi

pembobot yang digunakan dalam penelitian ini.

3. Membentuk matriks Wi

dari baris atau kolom ke-i dari matriks W

,

4. Menentukan nilai r dan

.

5. Selanjutnya melakukan simulasi gibbs sampling:

a. Tentukan nilai secara acak untuk parameter 𝛽

𝑖0

, 𝜎

0

, 𝛿

0

, 𝑉

𝑖0

, 𝛾

0

b. Untuk tiap observasi i = 1,…, n,



Bangkitkan 𝛽

_𝑖1

dari 𝑃(𝛽

_𝑖

|𝜎

0

_{, 𝛿}

0

_{, 𝑉}

𝑖0

, 𝛾

0

)



Bangkitkan 𝜎

1

dari 𝑃(𝜎|𝛿

0

, 𝑉

𝑖0

, 𝛾

0

)



Bangkitkan 𝑉

_𝑖1

dari 𝑃(𝑉

_𝑖

|𝛽

_𝑖1

, 𝜎

0

_{, 𝛿}

0

_{, 𝛾}

0

₎

c. Menggunakan nilai 𝛽

_𝑖1

, i= 1, …, n untuk memperbarui 𝛾

0

_{menjadi 𝛾}

1

d. Nilai 𝛿

1

_{diperoleh dari 𝑃(𝛿|𝜎}

1

_{, 𝑉}

𝑖1

, 𝛾

1

)

f. Ulangi langkah 1-5 sebanyak 550 bangkitan dengan 50 bangkitan pertama

dibuang.

6. Menentukan model RTGB terbaik, selanjutnya membandingkannya dengan

model RTG.

Penelitian ini menggunakan program Matlab 7.8.0 (R2009a) dan Minitab 14.0

dalam menganalisis data.

HASIL DAN PEMBAHASAN

Deskripsi Data

Peubah penjelas yang digunakan adalah jarak dari desa atau kelurahan ke

ibukota kabupaten atau kota (X

1

), banyaknya sarana kesehatan di desa (poskesdes,

polindes, posyandu, apotek dan toko khusus obat) per 1000 penduduk (X

2

), dan

persentase keluarga penerima ASKESKIN dalam setahun terakhir (X

3

). Nilai

jangkauan, minimum, maksimum, rata-rata dan simpangan baku dari ketiga

peubah penjelas dapat dilihat dari Tabel 1.

Tabel 1 Nilai jangkauan, minimum, maksimum, rata-rata dan simpanga baku

peubah penjelas

Peubah

Jangkauan Min Maks Rata-rata

Simpangan

Baku

Jarak desa-kabupaten (X

1

) 55.00

1.00 56.00

25.91

13.94

Sarana Kesehatan (X

2

)

1.76

0.91

2.67

1.50

0.36

ASKESKIN (X

3

)

60.62

11.07 71.69

34.72

17.78

Berdasarkan Tabel 1, simpangan baku pada peubah penjelas X

3

(persentase

keluarga yang menerima kartu ASKESKIN dalam setahun) cukup besar, yang

berarti bahwa jumlah penerima ASKESKIN di tiap desa/kelurahan beragam.

Simpangan baku pada peubah sarana kesehatan (X

2

) kecil, yang berarti bahwa

sarana kesehatan di desa/kelurahan di Kabupaten Jember cukup merata di tiap

desa atau kelurahan.

Sebelum melakukan pendugaan parameter, peubah-peubah penjelas harus

dipastikan berpengaruh terhadap peubah respon. Selain itu, antar peubah penjelas

tidak saling berkorelasi atau saling bebas. Untuk menunjukkan hal tersebut,

digunakan analisis korelasi Pearson. Korelasi pearson antar peubah ditunjukan

pada Tabel 2.

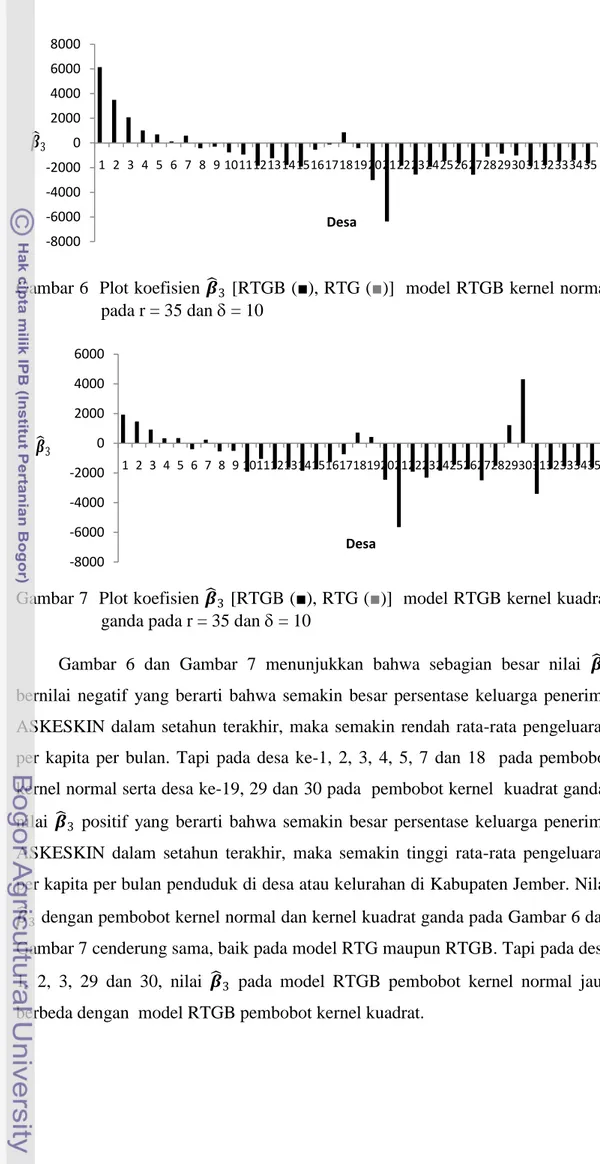
Tabel 2 Korelasi Pearson antar peubah

Peubah

Korelasi Pearson Nilai-p

Y dan X

1

-0.46*

0.01

Y dan X

2

0.69*

0.00

Y dan X

3

-0.38*

0.02

X

1

dan X

2

-0.26

0.13

X

1

dan X

3

-0.12

0.51

X

2

dan X

3

-0.23

0.19

Keterangan: * : nyata pada α = 5%

Nilai korelasi antar ketiga peubah penjelas dengan peubah respon pada

Tabel 2 nyata dengan taraf kepercayaan 95%, yang berarti bahwa semua peubah

penjelas berpengaruh terhadap peubah respon. Sedangkan semua nilai korelasi

antar peubah penjelas tidak nyata pada taraf kepercayaan 95%, sehingga antar

peubah penjelas tidak saling berkorelasi atau tidak terjadi multikolinearitas.

Ketiga peubah penjelas tersebut dapat langsung digunakan untuk keperluan

analisis selanjutnya.

Model RTGB

Sebelum digunakan model RTGB untuk analisis data, digunakan terlebih

dahulu analisis RTG yang diperoleh dari hasil penelitian Rahmawati pada tahun

2010. Berdasarkan penelitian Rahmawati (2010) diperoleh nilai lebar jendela

optimum yang dihasilkan dengan meminimumkan CV, yaitu 9.09 km untuk fungsi

pembobot kernel normal dan 27.48 km untuk fungsi pembobot kernel kuadrat

ganda. Nilai lebar jendela sebesar 9.09 km untuk fungsi pembobot kernel normal

menunjukkan bahwa jarak antar desa atau kelurahan yang kurang dari 9.09 km,

memberikan pengaruh yang cukup besar terhadap data yang diamati. Sedangkan

jika lokasi antar desa atau kelurahan sudah melebihi jarak 9.09 km, maka

pengaruhnya akan menurun seiring dengan semakin jauhnya jarak antar desa atau

kelurahan. Nilai lebar jendela sebesar 27.48 km untuk fungsi pembobot kernel

kuadrat ganda menunjukkan bahwa jarak antar desa atau kelurahan kurang dari

27.48 km, dianggap mempengaruhi data dengan semakin dekat jarak maka

semakin besar pengaruhnya terhadap data yang diamati. Sedangkan jarak antar

desa atau kelurahan yang lebih dari atau sama dengan 27.48 km, dianggap sudah

tidak mempengaruhi data yang diamati.

Berbeda dengan pendugaan model RTG yang menggunakan WLS,

pendugaan koefisien regresi pada model RTGB menggunakan Gibbs Sampling

dengan melakukan iterasi sebanyak 550 kali dimana 50 ulangan pertama dibuang.

Dengan menggunakan fungsi pembobot kernel normal dan kernel kuadrat ganda

serta berbagai nilai r (r = 8, 15, 25 dan 35) dan



(



= 1, 10 dan 100) maka

diperoleh penduga parameter model RTGB. Penduga parameter model RTGB

kernel normal dan kernel kuadrat ganda untuk berbagai prior r dan



pada

Lampiran 1 dan Lampiran 2. Berikut penduga koefisien model RTG dan model

RTGB kernel normal dan kuadrat ganda dengan r = 35 dan



= 10 pada Gambar 2

sampai Gambar 7.

Gambar 2 Plot koefisien 𝜷

₁

[RTGB (■), RTG (

■

)] model RTGB kernel normal

pada r = 35 dan



= 10

-15000 -10000 -5000 0 5000 10000 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435 Desa

𝜷

1

Gambar 3 Plot koefisien 𝜷

₁

[RTGB (■), RTG (

■

)] model RTGB kernel kuadrat

ganda pada r = 35 dan



= 10

Pada model regresi, nilai-nilai penduga parameter dapat dijadikan sebagai

pertimbangan besarnya kontribusi peubah penjelas terhadap peubah respon.

Berbeda dengan regresi linear global yang hasil penduga parameter untuk tiap

peubah sama untuk semua desa atau kelurahan, pada model RTG dan RTGB

menghasilkan penduga parameter yang dapat bernilai positif ataupun negatif pada

desa atau kelurahan yang berbeda untuk peubah yang sama. Sehingga suatu

peubah penjelas yang sama bisa memberi kontribusi negatif maupun positif

terhadap rata-rata pengeluaran per kapita desa atau kelurahan yang berbeda.

Gambar 2 dan Gambar 3 menunjukkan bahwa nilai 𝜷

₁

yang berbeda di tiap

desa atau kelurahan di Kabupaten Jember. Gambar 2 dan Gambar 3 juga

menunjukkan pola yang cenderung sama antara model RTG dan RTGB dengan

pembobot kernel normal dan kuadrat ganda, tapi ada beberapa desa yang

mempunyai pola yang berlawanan atau berbeda yaitu desa ke-4, 8, 9, dan 21.

sebagian besar nilai 𝜷

₁

model RTG dan RTGB kernel normal dan kuadrat ganda

bernilai negatif. Nilai negatif pada

𝜷

₁

berarti bahwa semakin jauh jarak dari desa

atau kelurahan ke ibukota kabupaten, maka semakin rendah rata-rata pengeluaran

per kapita per bulan. Tapi nilai 𝜷

1

pada desa ke- 1, 2, 3, 4, 8, 9, 18, 19, 20 dan 21

bernilai positif yang berarti bahwa semakin jauh jarak dari desa atau kelurahan ke

ibukota kabupaten, maka semakin tinggi rata-rata pengeluaran per kapita per

bulan. Gambar 2 dan Gambar 3 juga menunjukkan Nilai

𝜷

₁

dengan pembobot

kernel normal dan kernel kuadrat ganda yang cenderung sama, baik pada model

RTG maupun RTGB.

-15000 -10000 -5000 0 5000 10000 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435 Desa

𝜷

1

Gambar 4 Plot koefisien 𝜷

₂

[RTGB (■), RTG (

■

)] model RTGB kernel normal

pada r = 35 dan



= 10

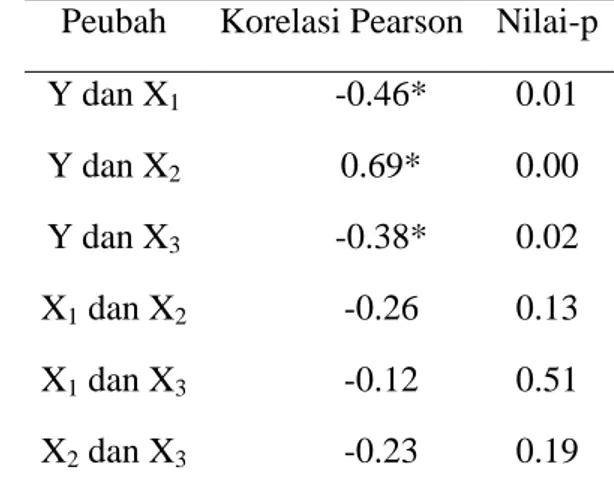
Gambar 5 Plot koefisien 𝜷

₂

[RTGB (■), RTG (

■

)] model RTGB kernel kuadrat

ganda pada r = 35 dan



= 10

Nilai

𝜷

₂

dengan pembobot kernel normal dan kernel kuadrat ganda pada

Gambar 4 dan Gambar 5 cenderung sama, baik pada model RTG maupun RTGB.

Tapi pada desa 1 nilai

𝜷

₂

pada model RTGB pembobot kernel normal jauh

berbeda dengan model RTGB pembobot kernel kuadrat. Sebagian besar nilai 𝜷

2

model RTG dan RTGB kernel normal dan kuadrat ganda bernilai positif yang

berarti bahwa semakin banyak sarana kesehatan di desa atau kelurahan di

Kabupaten Jember, maka rata-rata pengeluaran per kapita per bulan penduduk

desa semakin besar. Tapi ada beberapa desa atau kelurahan yang nilai 𝜷

₂

bernilai

negatif seperti desa ke- 5, 7, 20, 21, 29, 30 dan 31 yang berarti bahwa semakin

banyak sarana kesehatan di desa atau kelurahan tersebut, maka rata-rata

pengeluaran per kapita per bulan penduduk semakin kecil.

-300000 -200000 -100000 0 100000 200000 300000 400000 500000 600000 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435 Desa

𝜷

2 -200000 -100000 0 100000 200000 300000 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435 Desa

𝜷

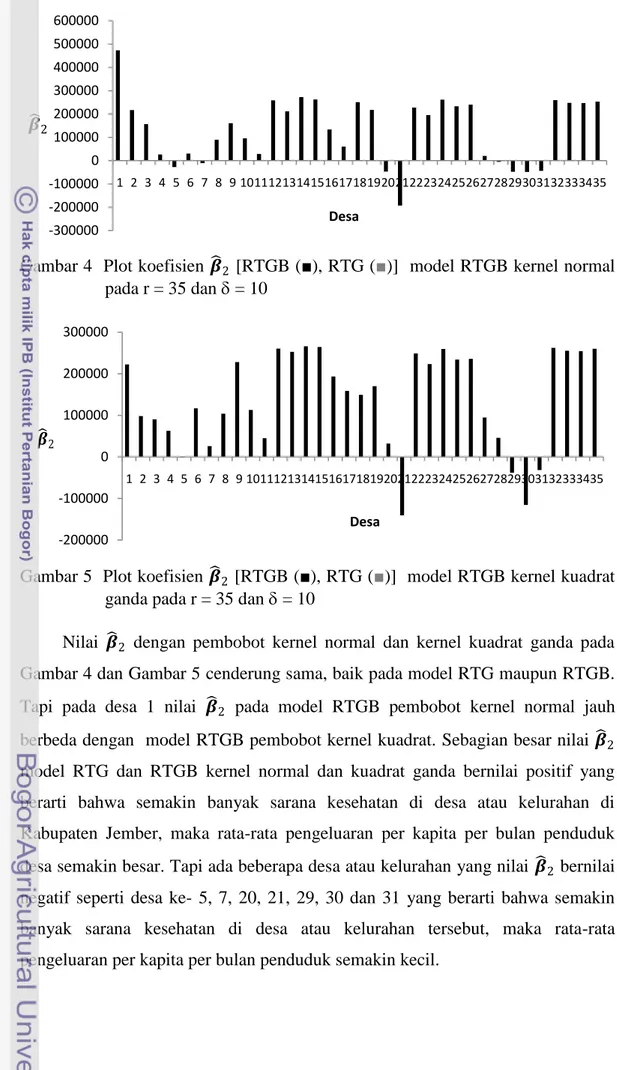
2

Gambar 6 Plot koefisien 𝜷

₃

[RTGB (■), RTG (

■

)] model RTGB kernel normal

pada r = 35 dan



= 10

Gambar 7 Plot koefisien 𝜷

₃

[RTGB (■), RTG (

■

)] model RTGB kernel kuadrat

ganda pada r = 35 dan



= 10

Gambar 6 dan Gambar 7 menunjukkan bahwa sebagian besar nilai

𝜷

₃

bernilai negatif yang berarti bahwa semakin besar persentase keluarga penerima

ASKESKIN dalam setahun terakhir, maka semakin rendah rata-rata pengeluaran

per kapita per bulan. Tapi pada desa ke-1, 2, 3, 4, 5, 7 dan 18 pada pembobot

kernel normal serta desa ke-19, 29 dan 30 pada pembobot kernel kuadrat ganda,

nilai

𝜷

₃

positif yang berarti bahwa semakin besar persentase keluarga penerima

ASKESKIN dalam setahun terakhir, maka semakin tinggi rata-rata pengeluaran

per kapita per bulan penduduk di desa atau kelurahan di Kabupaten Jember. Nilai

𝜷

3

dengan pembobot kernel normal dan kernel kuadrat ganda pada Gambar 6 dan

Gambar 7 cenderung sama, baik pada model RTG maupun RTGB. Tapi pada desa

1, 2, 3, 29 dan 30, nilai

𝜷

₃

pada model RTGB pembobot kernel normal jauh

berbeda dengan model RTGB pembobot kernel kuadrat.

-8000 -6000 -4000 -2000 0 2000 4000 6000 8000 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435 Desa

𝜷

₃ -8000 -6000 -4000 -2000 0 2000 4000 6000 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435 Desa

𝜷

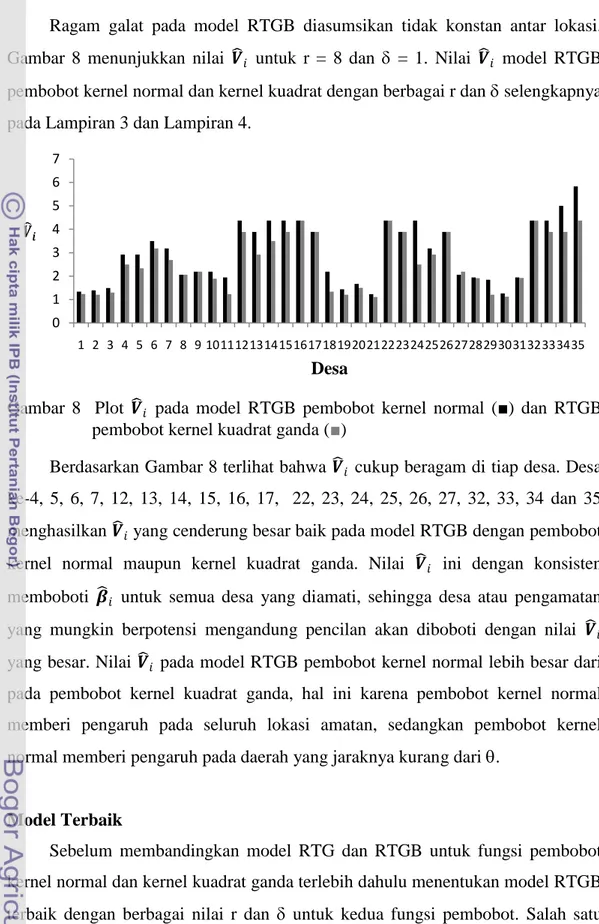
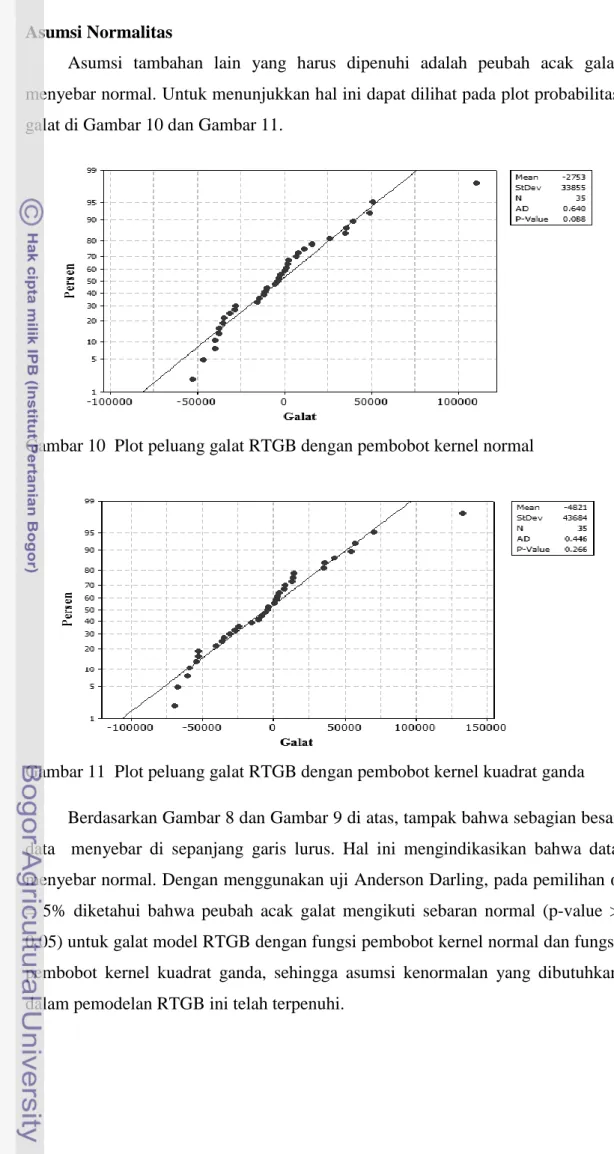
₃

Ragam galat pada model RTGB diasumsikan tidak konstan antar lokasi.

Gambar 8 menunjukkan nilai

𝑽

_𝑖

untuk r = 8 dan



= 1. Nilai

𝑽

_𝑖

model RTGB

pembobot kernel normal dan kernel kuadrat dengan berbagai r dan



selengkapnya

pada Lampiran 3 dan Lampiran 4.

Gambar 8 Plot

𝑽

𝑖

pada model RTGB pembobot kernel normal (■) dan RTGB

pembobot kernel kuadrat ganda (

■

)

Berdasarkan Gambar 8 terlihat bahwa 𝑽

_𝑖

cukup beragam di tiap desa. Desa

ke-4, 5, 6, 7, 12, 13, 14, 15, 16, 17, 22, 23, 24, 25, 26, 27, 32, 33, 34 dan 35

menghasilkan 𝑽

_𝑖

yang cenderung besar baik pada model RTGB dengan pembobot

kernel normal maupun kernel kuadrat ganda. Nilai

𝑽

_𝑖

ini dengan konsisten

memboboti

𝜷

_𝑖

untuk semua desa yang diamati, sehingga desa atau pengamatan

yang mungkin berpotensi mengandung pencilan akan diboboti dengan nilai

𝑽

_𝑖

yang besar. Nilai 𝑽

𝑖

pada model RTGB pembobot kernel normal lebih besar dari

pada pembobot kernel kuadrat ganda, hal ini karena pembobot kernel normal

memberi pengaruh pada seluruh lokasi amatan, sedangkan pembobot kernel

normal memberi pengaruh pada daerah yang jaraknya kurang dari



.

Model Terbaik

Sebelum membandingkan model RTG dan RTGB untuk fungsi pembobot

kernel normal dan kernel kuadrat ganda terlebih dahulu menentukan model RTGB

terbaik dengan berbagai nilai r dan



untuk kedua fungsi pembobot. Salah satu

indikator yang dapat digunakan adalah R

2

. Nilai R

2

yang lebih tinggi

mengindikasikan model yang lebih baik. Pada penelitian ini, nilai R

2

diperoleh

dari pemodelan antar Y amatan dan Y duga dari model RTGB untuk berbagai

0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435

Desa

𝑽𝒊

nilai r dan



. Indikator lainnya adalah kuadrat tengah galat (KTG) atau mean

square error. Nilai KTG yang lebih kecil mengindikasikan model yang lebih baik.

Tabel 3 dan Tabel 4 menunjukkan nilai R

2

dan KTG untuk model RTGB dengan

fungsi pembobot kernel normal dan model RTGB dengan fungsi pembobot kernel

kuadrat ganda untuk berbagai r dan



.

Tabel 3 Nilai R

2

dan KTG model RTGB pembobot kernel normal



r

8

15

25

35

R

2

(%)

KTG

(10

9

)

R

2

(%)

KTG

(10

9

)

R

2

(%)

KTG

(10

9

)

R

2

(%)

KTG

(10

9

)

1

89.20 1.51 91.20 1.22 91.70 1.15 91.70 1.14

10

89.40 1.49 91.50 1.17 91.70 1.15 91.80 1.12

100 89.30 1.50 91.40 1.19 91.70 1.15 91.80 1.13

Tabel 4 Nilai R

2

dan KTG model RTGB pembobot kernel kuadrat ganda



r

8

15

25

35

R

2

(%)

KTG

(10

9

)

R

2

(%)

KTG

(10

9

)

R

2

(%)

KTG

(10

9

)

R

2

(%)

KTG

(10

9

)

1

83.40 2.29 84.80 2.08 85.70 1.96 86.10 1.89

10

84.90 2.08 85.40 1.98 85.30 2.00 86.30 1.87

100 82.80 2.33 84.80 2.09 85.30 2.01 85.80 1.94

Berdasarkan Tabel 3 dan Tabel 4 terlihat bahwa pada prior r = 35 dan



=

10, model RTGB dengan pembobot kernel normal dan pembobot kernel kuadrat

ganda adalah model RTGB dengan nilai R

2

tertinggi dan KTG terkecil. Model

RTGB menghasilkan nilai R

2

sebesar 91.8% dan KTG sebesar 1.12 x 10

9

untuk

pembobot kernel normal dan R

2

sebesar 86.3% dan KTG sebesar 1.87 x 10

9

untuk

pembobot kernel kuadrat ganda, sehingga prior r = 35 dan



= 10 adalah prior

yang menghasilkan model RTGB terbaik untuk kedua fungsi pembobot yang

digunakan. Tabel 3 dan Tabel 4 juga menunjukkan bahwa semakin besar prior r,

maka nilai R

2

cenderung makin besar dan nilai KTG yang menurun. Tabel 3 dan

Tabel 4 juga terlihat bahwa prior



tidak cukup signifikan berpengaruh terhadap

model.

Setelah menentukan model RTGB terbaik, selanjutnya membandingkannya

dengan model RTG pada penelitian Rahmawati (2010). Tabel 5 menunjukkan

nilai R

2

dan KTG untuk model RTG dan RTGB dengan pembobot kernel normal

dan pembobot kernel kuadrat ganda.

Tabel 5 Nilai R

2

dan KTG model RTG dan RTGB dengan pembobot kernel

normal dan pembobot kernel kuadrat ganda

Model

R

2

KTG

RTG kernel normal

85.30%

2.00



10

9

RTGB kernel normal

91.80%

1.12



10

9

RTG kernel kuadrat ganda

82.20%

2.40



10

9

RTGB kernel kuadrat ganda 86.30%

1.87



10

9

Berdasarkan Tabel 5, model RTGB dengan pembobot kernel normal adalah

model terbaik yang menghasilkan nilai R

2

tertinggi dan KTG terkecil dari model

RTG dengan fungsi pembobot kernel normal dan kernel kuadrat ganda maupun

model RTGB dengan pembobot kernel kuadrat ganda. Tabel 5 juga menunjukkan

bahwa pada pembobot kernel normal dan kernel kuadrat ganda, model RTGB

lebih baik dari pada model RTG.

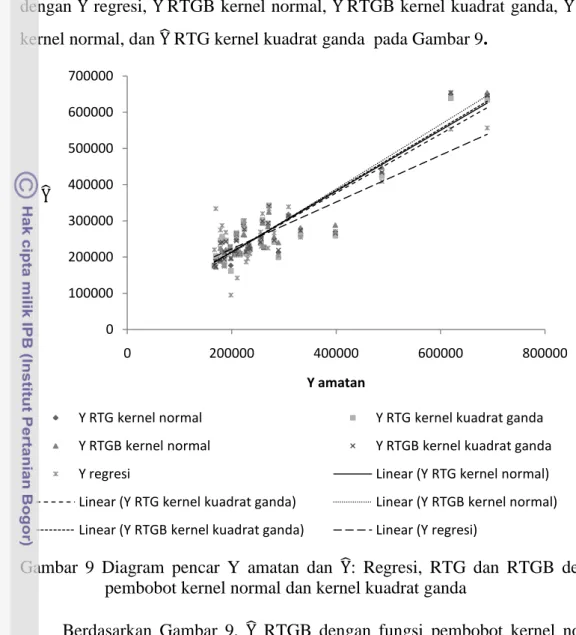
Untuk menunjukkan bahwa model RTGB dengan pembobot kernel normal

adalah model yang terbaik juga dipertegas pada diagram pencar antara Y amatan

dengan

Y

regresi, Y RTGB kernel normal, Y RTGB kernel kuadrat ganda, Y RTG

kernel normal, dan Y

RTG kernel kuadrat ganda pada Gambar 9.

Gambar 9 Diagram pencar Y amatan dan

Y

: Regresi, RTG dan RTGB dengan

pembobot kernel normal dan kernel kuadrat ganda

Berdasarkan Gambar 9,

Y

RTGB dengan fungsi pembobot kernel normal

lebih mendekati Y amatan dibandingkan dengan

Y

model RTGB dengan fungsi

pembobot kernel kuadrat ganda,

Y

RTG dengan fungsi pembobot kernel normal

dan kernel kuadrat ganda maupun Y

regresi, sehingga model RTGB dengan fungsi

pembobot kernel normal adalah model terbaik untuk pendugaan rata-rata

pengeluaran per kapita per bulan desa atau kelurahan di Kabupaten Jember.

0 100000 200000 300000 400000 500000 600000 700000 0 200000 400000 600000 800000 Y amatan

Y RTG kernel normal Y RTG kernel kuadrat ganda

Y RTGB kernel normal Y RTGB kernel kuadrat ganda

Y regresi Linear (Y RTG kernel normal)

Linear (Y RTG kernel kuadrat ganda) Linear (Y RTGB kernel normal)

Linear (Y RTGB kernel kuadrat ganda) Linear (Y regresi)

Asumsi Normalitas

Asumsi tambahan lain yang harus dipenuhi adalah peubah acak galat

menyebar normal. Untuk menunjukkan hal ini dapat dilihat pada plot probabilitas

galat di Gambar 10 dan Gambar 11.

Gambar 10 Plot peluang galat RTGB dengan pembobot kernel normal

Gambar 11 Plot peluang galat RTGB dengan pembobot kernel kuadrat ganda

Berdasarkan Gambar 8 dan Gambar 9 di atas, tampak bahwa sebagian besar

data menyebar di sepanjang garis lurus. Hal ini mengindikasikan bahwa data

menyebar normal. Dengan menggunakan uji Anderson Darling, pada pemilihan α

= 5% diketahui bahwa peubah acak galat mengikuti sebaran normal (p-value >

0.05) untuk galat model RTGB dengan fungsi pembobot kernel normal dan fungsi

pembobot kernel kuadrat ganda, sehingga asumsi kenormalan yang dibutuhkan

dalam pemodelan RTGB ini telah terpenuhi.

KESIMPULAN DAN SARAN

KESIMPULAN

Berdasarkan berbagai prior r dan



yang digunakan dalam analisis model

RTGB dengan fungsi pembobot kernel normal dan fungsi pembobot kernel

kuadrat ganda untuk pendugaan rata-rata pengeluaran per kapita per bulan desa

atau kelurahan di Kabupaten Jember, prior r = 35 dan



= 10 adalah prior yang

menghasilkan model RTGB terbaik untuk kedua fungsi pembobot. Jika

dibandingkan dengan model RTG, maka model RTGB dengan fungsi pembobot

kernel normal adalah model terbaik dengan KTG sebesar 1.12 x 10

9

dan R

2

sebesar 91.8%.

SARAN

Penelitian ini fokus pada permasalahan ragam tidak konstan antar lokasi

dengan menggunakan pembobot kernel dengan lebar jendela yang sama untuk

semua lokasi, sehingga penelitian berikutnya disarankan menggunakan pembobot

kernel adaptif dengan lebar jendela yang berbeda-beda di tiap lokasi. Pada

pembobot kernel adaptif, titik-titik amatan yang berdekatan atau mengumpul

menghasilkan lebar jendela yang kecil sedangkan titik-titik amatan yang

berpencar menghasilkan lebar jendela yang besar, sehingga diharapkan dapat

menghasilkan galat model yang lebih kecil.

Pendugaan parameter pada model RTGB hanya berlaku pada lokasi amatan

dan tidak dapat digunakan untuk menduga parameter di luar lokasi amatan.

Penelitian ini dapat dikembangkan untuk menduga parameter di luar lokasi

amatan dengan menggunakan metode interpolasi.

DAFTAR PUSTAKA

Arisanti R. 2010. Model Regresi Spasial untuk Deteksi Faktor-Faktor Kemiskinan

di Provinsi Jawa Timur [tesis]. Bogor: Program Pascasarjana, Institut

Pertanian Bogor.

BPS [Badan Pusat Statistik]. 2005. Identifikasi dan Penentuan Desa Tertinggal

2005. Buku II = Jawa. Jakarta: Badan Pusat Statistik.

BPS [Badan Pusat Statistik]. 2008. Data dan Informasi Kemiskinan 2008. Jakarta:

Badan Pusat Statistik.

BPS [Badan Pusat Statistik]. 2009. Kabupaten Jember dalam Angka 2009.

Kabupaten Jember: Kerjasama Badan Perencanaan Pembangunan dengan

Badan Pusat Statistik

BPS [Badan Pusat Statistik]. 2011. Berita Resmi Statistik No. 45/07/Th. XIV, 1

Juli

2011.

http://www.bps.go.id/brs_file/kemiskinan_01jul11.pdf

[30

Desember 2011]

BPS [Badan Pusat Statistik]. 2012. Meta Data Subdit Statistik Kerawanan Sosial.

http://www.bps.go.id/menutab.php?tabel=1&kat=1&id_subyek=23 [16 Juli

2012]

Chan HS. 2008. Incorporating the Concept of „Community‟ into A

Spatially-Weighted Local Regression Analysis [thesis]. Canada: Department of

Geodesy and Geomatics Engineering, University of New Brunswick.

Fotheringham AS, Brundson C, Chartlon M. 2002. Geographically Weighted

Regression, the Analysis of spatially varying relationships. John Wiley and

Sons, LTD.

LeSage JP. 1998. Spatial Econometric [paper]. Department of Economics,

University of Toledo.

LeSage JP. 1999. The Theory and Practice of Spatial Econometrics [paper].

Department of Economics, University of Toledo.

LeSage JP. 2001. A Family of Geographically Weighted Regression Models.

Journal of Geographic Information Science Vol. 5, No. 2, Department of

Economics University of Toledo.

Meilisa M. 2010. Model Otoregresi Simultan dan Otoregresi Bersyarat untuk

Analisis Kemiskinan di Provinsi Jawa Timur [tesis]. Bogor: Program

Pascasarjana, Institut Pertanian Bogor.

Rahmawati R. 2010. Model Regresi Terboboti Geografis dengan Pembobot

Kernel Normal dan Kernel Kuadrat Ganda untuk Data Kemiskinan (Kasus

35 Desa atau Kelurahan di Kabupaten Jember) [tesis]. Bogor: Program

Pascasarjana, Institut Pertanian Bogor.

Schabenberger O, Gotway CA. 2005. Statistical Methods for Spatial Data

Analysis. Chapman & Hall/CRC.

Lampiran 1. Penduga parameter model RTGB pembobot kernel normal



r = 8 dan



= 1

Desa b0 b1 b2 b3 𝑌 RTGB PASEBAN -827090.0 5070.0 486290.0 5970.0 282372.07 GUMUKMAS -408170.0 4830.0 244150.0 3260.0 238742.85 TEMBOKREJO -294260.0 5580.0 167320.0 2160.0 225673.20 WRINGIN TELU 22870.0 1550.0 97900.0 130.0 242246.54 AMPEL 220510.0 -2810.0 77670.0 -150.0 215532.84 KESILIR 144400.0 -2040.0 124470.0 -650.0 217816.59 SABRANG 198430.0 -2610.0 94190.0 -320.0 247681.21 SIDODADI 149440.0 400.0 82390.0 -500.0 257379.77 PACE 42600.0 -190.0 155760.0 -470.0 221968.90 SEMPOLAN 194590.0 -3110.0 111130.0 -920.0 265047.55 GARAHAN 240080.0 -760.0 28590.0 -890.0 216829.53 MRAWAN 48630.0 -4520.0 242460.0 -1820.0 259526.87 KEMUNING SARI KIDUL 32710.0 -2490.0 220660.0 -1320.0 327888.54 SUKAMAKMUR 19600.0 -3630.0 250000.0 -1680.0 272378.99 WIROWONGSO 30850.0 -4340.0 250180.0 -1810.0 300693.66 KARANG SEMANDING 43860.0 -1210.0 170730.0 -890.0 213823.36 BALUNG KIDUL 88260.0 -1700.0 152590.0 -770.0 228590.26 GADINGREJO -277880.0 4250.0 228490.0 610.0 283791.42 WRINGIN AGUNG -194950.0 3190.0 219990.0 -250.0 225684.02 PRINGGOWIRAWAN 419410.0 -160.0 -65280.0 -3220.0 216911.18 JATIROTO 713010.0 -760.0 -187310.0 -6320.0 209091.46 SUKOREJO 23000.0 -2120.0 219090.0 -1590.0 194228.17 GAMBIRONO 52770.0 -1160.0 183460.0 -1820.0 234975.88 SERUT 50470.0 -4610.0 244140.0 -1860.0 181093.58 KEMUNINGLLOR 93530.0 -5980.0 228640.0 -1740.0 206617.01 SUMBER PINANG 89770.0 -4820.0 227530.0 -1880.0 225748.68 KALISAT 532510.0 -7980.0 23260.0 -2730.0 280627.88 SUREN 456960.0 -5840.0 -17320.0 -1320.0 215131.43 RANDU AGUNG 592400.0 -9990.0 -47890.0 -860.0 196188.85 SUMBERJAMBE 579910.0 -9240.0 -47900.0 -1010.0 178476.61 ARJASA 643550.0 -9970.0 -43860.0 -1830.0 173813.88 TEGAL BESAR 43130.0 -4580.0 245880.0 -1780.0 320180.49 KARANGREJO 68500.0 -6010.0 237690.0 -1650.0 636638.06 SUMBERSARI 61290.0 -4980.0 237970.0 -1710.0 625703.15 JEMBER LOR 50180.0 -4950.0 244420.0 -1740.0 426777.53

Lampiran 1. Lanjutan…



r = 15 dan



= 1

Desa b0 b1 b2 b3 𝑌 RTGB PASEBAN -745460.0 4970.0 439040.0 5750.0 282888.90 GUMUKMAS -385590.0 5000.0 224670.0 3310.0 238201.63 TEMBOKREJO -255350.0 5220.0 153240.0 1990.0 225477.31 WRINGIN TELU 14070.0 3860.0 27960.0 990.0 221510.04 AMPEL 394120.0 -3980.0 -32440.0 740.0 225610.60 KESILIR 252590.0 -1940.0 36430.0 80.0 237906.83 SABRANG 334220.0 -2980.0 -6310.0 660.0 254073.80 SIDODADI 130110.0 530.0 92250.0 -430.0 257978.65 PACE 24540.0 230.0 158790.0 -360.0 227200.65 SEMPOLAN 209860.0 -3150.0 96530.0 -760.0 261370.74 GARAHAN 243760.0 -760.0 27550.0 -950.0 217034.58 MRAWAN 25920.0 -5200.0 256660.0 -1790.0 252548.04 KEMUNING SARI KIDUL 6380.0 -1200.0 219770.0 -1390.0 326421.20 SUKAMAKMUR -5150.0 -3880.0 267410.0 -1880.0 263584.38 WIROWONGSO 21720.0 -5610.0 262080.0 -1950.0 294592.90 KARANG SEMANDING 82480.0 -1000.0 132280.0 -620.0 215220.90 BALUNG KIDUL 189200.0 -1840.0 75020.0 -180.0 237809.25 GADINGREJO -313700.0 4780.0 236160.0 790.0 286061.84 WRINGIN AGUNG -209110.0 3090.0 230860.0 -100.0 226673.24 PRINGGOWIRAWAN 399640.0 -100.0 -52350.0 -3200.0 221038.29 JATIROTO 777530.0 -1400.0 -207480.0 -6630.0 208777.19 SUKOREJO 23160.0 -2260.0 224150.0 -1740.0 191665.58 GAMBIRONO 60820.0 -1260.0 194230.0 -2440.0 226644.11 SERUT 52290.0 -6450.0 259550.0 -1900.0 178522.25 KEMUNINGLLOR 101000.0 -8880.0 236080.0 -1480.0 207999.35 SUMBER PINANG 70960.0 -5850.0 239710.0 -1630.0 226658.11 KALISAT 529080.0 -8000.0 22020.0 -2620.0 281075.56 SUREN 416250.0 -5230.0 -7260.0 -1100.0 214587.17 RANDU AGUNG 594280.0 -10110.0 -49370.0 -780.0 198027.47 SUMBERJAMBE 584830.0 -9370.0 -47350.0 -1040.0 178487.47 ARJASA 645140.0 -9910.0 -44480.0 -1870.0 173111.28 TEGAL BESAR 35910.0 -6450.0 258840.0 -1840.0 319794.73 KARANGREJO 62970.0 -8380.0 248270.0 -1470.0 654488.92 SUMBERSARI 73360.0 -7980.0 242100.0 -1520.0 644470.20 JEMBER LOR 52220.0 -6700.0 252010.0 -1680.0 440413.49