6.1 Pengertian Umum 6.1 Pengertian Umum
Banyak permasa
Banyak permasalahan yang datalahan yang datanya dinyatakan oleh nya dinyatakan oleh leblebih dari sebuah variabel. ih dari sebuah variabel. HubunganHubungan antara dua atau le
antara dua atau lebih bih variabel variabel dapat dinyatakan sedapat dinyatakan se cara matematika sehincara matematika sehingga merupakan suatu gga merupakan suatu mmoodedell yang dapat digunakan untuk berbagai keperluan analisis, misalnya: peramalan (prediction), yang dapat digunakan untuk berbagai keperluan analisis, misalnya: peramalan (prediction), perpanjangan (
perpanjangan ( exteextension)nsion), , perbaikan perbaikan atau penatau pengecekan gecekan ketelketel itian itian data, atau data, atau pepe ngisan dangisan datta a papada da prprioiodede kosong untuk kas
kosong untuk kasus hidrologi.us hidrologi. Analisis re Analisis regresi gresi adalah analisis yang membahas hubungan adalah analisis yang membahas hubungan fungsiofungsionalnal dua variabel atau lebih.
dua variabel atau lebih. Analisis Analisis korelasi korelasi (correlation (correlation analisys)analisys) adalah analisis yang membahasadalah analisis yang membahas tentang derajat hubungan dalam analisis regresi disebut. Tujuan regresi adalah untuk melihat tentang derajat hubungan dalam analisis regresi disebut. Tujuan regresi adalah untuk melihat hubungan antara 2
hubungan antara 2 variabel variabel atau lebiatau lebih.h. 6.2 Nil
6.2 Nilai Haraai Harapanpan Misalkan
Misalkan
adalah variabel acak dengan distribusi probabilitas adalah variabel acak dengan distribusi probabilitas
..MeanMean atau atau ekspekekspektasitasi atau nilai harapan dari X adalahatau nilai harapan dari X adalah
,,
(6. 1) (6. 1) ,,
−∞
−∞
∞∞
(6. 2) (6. 2) Ekspektasi atau nilEkspektasi atau nilai rata-rata ataai rata-rata atau u nilnilaiai meanmean dari variabe dari variabel acal acakk
dengan fungsi kerapatan dengan fungsi kerapatan peluangpeluang
dan nilaidan nilai x x i i untuk untuk1,2,...
1,2,...
adalah adalah
∞∞
=
=
(6. 3) (6. 3) Teorema 1 Teorema 1 JikaJika
adalah variabel acak diskrit, nilai mean dari fungsiadalah variabel acak diskrit, nilai mean dari fungsi
adalah adalah
(6. 4) (6. 4) Teorema 2 Teorema 2 MisalkanMisalkan
dandan
adalah variabel acak diskrit maka adalah variabel acak diskrit maka a.a. untuk seuntuk sembarang konstantambarang konstanta a a E ,,E a
a aadandan E E a
aX X
aaE E X
Xb.
b. E X Y E
X Y E
E X
X E
E Y
Yc.
c. terdapat kontantaterdapat kontanta a a b , , b c ,,c
E E aaX X bbY Y c c aaE E X X bbE E Y Y c c Sifat-sifat ekspektasi: Sifat-sifat ekspektasi:a. Jika X merupakan variabel acak dengan pdf f x ( x ) danu( X ) adalah fungsi dari X , maka ekspektasi dariu( X ) adalah:
, jika X diskrit
, jika X kontinu
x x x u x f x E u X u x f x dx (6. 5) b. Sifat linear ekspektasi
E ag X bh X aE g X bE h X (6. 6) 6.3 VariansiMean dari variabel acak X adalah suatu ni lai yang penting dalam statistik karena ni lai tersebut menggambarkan dimana distribusi probabilitas berpusat. Meskipun demiki an mean tidak cukup untuk memberikan gambaran tentang bentuk suatu distribusi.Untuk mengetahui bentuk suatu distrib usi, perlu diketahui variabilitas distribusi tersebut. Salah satu ukuran variabilitas dalam statistik adalah variansi. Variansi dari variabel acak X atau variansi dari distribusi probabilitas X dinyatakan dengan
Var X atau dinotasikan dengan 2
x atau
2
.Misalkan X adalah variabel acak dengan distribusi probabil itas f x
danmean . Variansidari X adalah
2
2
2 x E X x f x , jika X diskrit (6. 7)
2 2 2 E X x f x dx , jika X kontinu (6. 8) Akar kuadrat positif ddari variansi
dinamakan standar deviasi dari
.Teorema 3
Variansi variabel acak X adalah
2 2 2 E X (6. 9) Bukti :Untuk kasus diskrit dapat dituliskan
2 2 2 2 2 x x x f x x x f x
2
2
2 x x x x f x xf x f xkarena
xxf x dan
1x
f x untuk setiap distribusi probabilitas diskrit maka
2
2 2 2 2 x x f x sehingga diperoleh
2
2 2 2 2 x x f x E X (6. 10) Nilai –
disebut penyimpangan suatu pengamatan dari rataannya. Karena penyi mpangan ini dikuadratkan lalu dirata-ratakan, maka
akan lebih kecil untuk kelompok nilai
yang dekat dengan
dibandingkan dengan kelompok nilai
yang jauh dari
.Dengan kata lain, jika nilai-nilai
cenderung terkonsentrasi di dekat rataannya, maka variansinya kecil. Sedangkan jika jauh dari rataan maka variansinya besar.Variansi untuk peubah acak lain yang bergantung pada
,
yaitu
, diberikan dalam Teorema 4.Misalkan
adalah peubah acak dengan distribusi peluang
. Variansi dari peubah acak
adalah:
(
)
∑ [(
)]
,
(6. 11)
(
)
∫ [(
−∞
∞
)]
,
(6. 12) 6.4 Sifat-Sifat Variansi Teorema 5.Jika a dan b adalah konstanta maka
+
(6. 13) Akibat 1: Jika a = 1, maka
+
(6. 14) Akibat 2: Jika b = 0, maka
Teorema 6.
Jika X dan Y adalah peubah acak dengan distribusi peluang
,
maka :
+
2
(6. 16) Akibat 1: Jika X dan Y peubah acak saling be bas, maka:
+
(6. 17) Akibat 2: Jika X dan Y variabel random saling bebas, maka:
−
(6. 18) 6.5 Kovariansi
Salah satu ukuran kekuatan hubungan li near antara dua variabel acak kontinu adalah dengan menentukan seberapa banyak kedua variabel tersebut co-vary, yaitu bervariasi bersama-sama. Jika salah satu variabel meningkat (atau menurun) sebagai akibat peningkatan (atau penurunan) variabel pasangannya, maka dua variabel te rsebut dinamakan covary. Namun ji ka satu variabel tidak berubah dengan meningkatnya (atau penurunan) variabel l ain, maka variabel tersebut tidak co -vary. Statistik untuk mengukur berapa banyak kedua variabel covary dalam sampel pengamatan adalah kovarian.
Selain mengukur besarnya kekuatan hubungan di antara dua variabel, kovarian juga menentukan arah hubungan dari kedua variabel tersebut.
Apabila nilainya positif, berati bahwa apabila nilai x berada di atas nilai rata-ratanya, maka nilai y juga berada di atas nilai rata-rata y, dan sebaliknya (Searah).
Nilai kovarian negatif menunjukkan bahwa apabila nilai x berada di atas nilai rata-ratanya sedangkan nilai y berada di bawah nilai rata-ratanya (berlawanan arah).
Terakhir, apabila nilai kovarian mendekati nol, menandakan bahwa kedua variabel tersebut tidak saling berhubungan.
Jika
dan
dua peubah acak bebas dengan rataan x dan y, maka kovarians peubah acak
dan
didefinisikan sebagai
[
(
)]
(6. 19) Misalkan
dan
adalah variabel acak dengan distribusi peluang gabungan,.
Kovariansi dari
dan
adalah
[
(
)]
(
)
,,
Dan
[
(
)]
−∞
∞
(
)
∞
−∞
, ,
(6. 21) Interpretasi:• Kovariansi antara dua peubah acak menunjukkan sif at asosiasi (hubungan) antara keduanya; • Jika kedua peubah tersebut bergerak kearah yang sama (nilai
berada di atas nilairata-ratanya, maka nilai
juga berada di atas nilai rata-rata y) maka hasil kali
cenderung bernilai positif;• Jika kedua peubah tersebut bergerak ke arah berlawanan (nilai
berada di atas nilairata-ratanya sedangkan nilai
berada di bawah nil ai rata-ratanya), maka hasil kali
cenderung akan bernilai negatif.• Terakhir, apabila ni lai kovarian mendekati nol , menandakan bahwa kedua variabel tersebut
tidak saling berhubungan.
• Tanda kovariansi (+ atau -) menunjukkan apakah hubungan antara kedua peubah acak positif
atau negatif.
Rumus alternatif untuk kovariansi:
[
(
)]
(6. 22) 6.5.1 Sifat-Sifat Kovariansi
Sifat- sifat kovarian adalah sebagai berikut Jika X dan Y diskrit:
< > ,
(6. 23)
< > ,
(6. 24)
< > ,
(6. 25) Jika X dan Y kontinyu
< > ,
∞
−∞
∞
−∞
(6. 26)
< > ,
∞
−∞
∞
−∞
(6. 27)
< > ,
∞
−∞
∞
−∞
(6. 28) 6.6 Persamaan KorelasiPersaman korelasi antara nilai
dan
adalah,
,1 ≤ , ≤ 1
(6. 29) hasil perhitungan dari persamaan 2.11 disebut sebagai harga/notasi Korelasi. Penjelasan dari harga/notasi korelasi adalah sebagai berikut :
• HARGA (-)
Ada hubungan tapi terbalik (jika
mengecil maka
membesar atau sebaliknya)• HARGA (+)
Ada hubungan tetapi sebanding (
mengecil maka
mengecil atau sebaliknya)• HARGA (0)
Tidak ada hubungan
Contoh Soal 6.1 :
Berikut ini adalah fungsi distribusi probabil itas bersama antara variabel X dan Y. Carilah kovariansi X dg Y f(x,y) x Jumlah baris 0 1 2 h(y) y 0 3/28 29/28 3/28 15/28 1 3/14 3/14 0 6/14 2 1/28 0 0 1/28 g(x) 10/28 15/28 3/28 1
Langkah 1:
Pertama hitung mean masing-masing variabel:
Langkah 2:
Kemudian hitung E(XY)=
E(XY)=0+0+0+0+3/14+0+0+0+0 = 3/14 Langkah 3:
6.7 Analisis Regresi
Analisis regresi mempelajari bentuk hubungan antara satu atau lebih peubah bebas
dengan satu peubah tak bebas
. Dalam penelitian peubah bebas
biasanya peubah yang ditentukan oleh peneliti secara bebas misalnya dosis obat, lama penyimpanan, kadar zat pengawet, umur ternak dan sebagainya. Disamping itu peubah bebas bisa juga berupa peubah tak bebasnya, misalnya dalam pengukuran panjang badan dan berat badan sapi, karena panjang badan l ebih mudah diukur maka panjang badan dimasukkan kedalam peubah bebas
, sedangkan berat badan dimasukkan peubah tak bebas.
sedangkan peubah tak bebas
dalam peneli tian berupa respon yang diukur akibat perlakuan/peubah bebas
. Misal nya jumlah sel darah merah akibat pengobatan dengan dosi s tertentu, jumlah mikroba daging setelah disimpan beberapa hari, berat ayam pada umur tertentu dan sebagainya.Bentuk hubungan antara peubah bebas
dengan peubah tak bebas
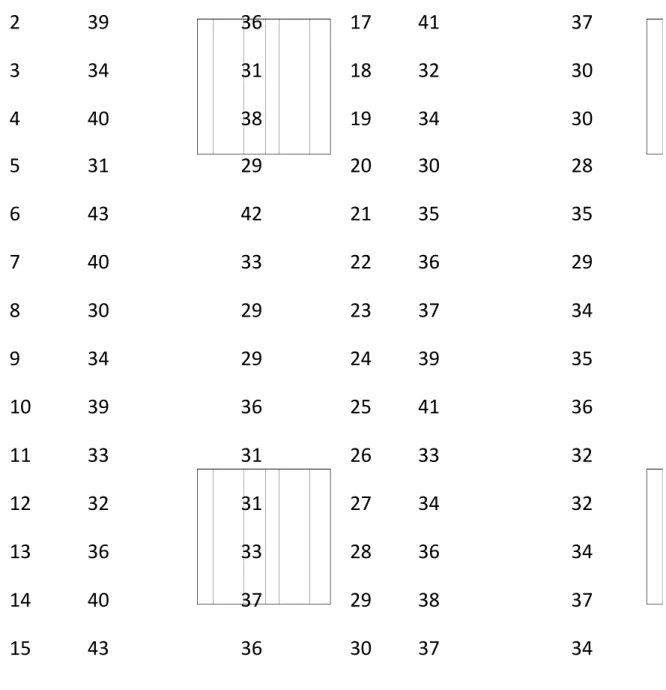
bisa dalam bentuk polinom derajat satu (linear) polinom derajat dua (kuadratik). Polinom derajat tiga (Kubik) dan seterusnya. Disamping i tu bisa juga dalam bentuk lain misalnya eksponensial, logaritma, sigmoid dan sebagainya. Bentuk-bentuk ini dalam analisis regresi-korelasi biasanya ditransformasi supaya menjadi bentuk polinom.Untuk menjelaskan bagaimana hubungan antara dua variabel, perhatikan data yang tercantum dalam tabel berikut :
HARI KE PENGUNJUNG (Xi) BELANJA (Yi) HARI KE PENGUNJUNG (Xi) BELANJA (Yi) 1 35 32 16 40 38 4 / 3 28 / 3 * 2 28 / 15 * 1 14 / 5 * 0 ) ( ] [
x X E X xg x 2 / 1 28 / 1 * 2 7 / 3 * 1 28 / 15 * 0 ) ( ] [
xY E Y yh y
0 * ) 2 * 2 ( ) 0 )( 1 * 2 ( ) 28 / 1 )( 0 * 2 ( ) 0 )( 2 * 1 ( ) 14 / 3 )( 1 * 1 ( ) 14 / 3 ( * ) 0 * 1 ( ) 28 / 3 )( 2 * 0 ( ) 28 / 9 )( 1 * 0 ( ) 28 / 3 )( 0 * 0 ( ) , ( ] [ x y y x xyf XY E 56 9 ) 2 1 )( 4 3 ( 14 3 ] [ Y X XY E XY 2 3 4 5 6 7 8 9 10 11 12 13 14 15 39 34 40 31 43 40 30 34 39 33 32 36 40 43 36 31 38 29 42 33 29 29 36 31 31 33 37 36 17 18 19 20 21 22 23 24 25 26 27 28 29 30 41 32 34 30 35 36 37 39 41 33 34 36 38 37 37 30 30 28 35 29 34 35 36 32 32 34 37 34
Tabel 6. 1 Banyak pengunjung dan belanja di suatu toko swalayan selama 30 hari
Tabel 2.1 merupakan gambaran banyak pengunjung (dinyatakan dengan
) dan yang berbelanja (dinyatakan dengan
) yang telah dicatat oleh seseorang pengusaha di tokonya.Kebiasaan yang digunakan dalam penentuan simbol -simbol yang lazim, ialah
untuk hal yang diperkirakan lebih tepat dapat digolongkan ke dalam variabel yang sifatnya bebas, sedangkan
untuk variabel yang diperkirakan akan bergantung pada
.Bentuk dari model persamaan regresi untuk populasi secara umum adalah sebgai berikut
X
X
X
k m
f
Y
, ,..., / , ,..., 2 1 2 1 (6. 30) Dimana
1,
,...,2
m parameter-parameter yang terdapat dalam regresi itu. Regresi yangsederhana untuk populasi de ngan sebuah variabel bebas yang dikenal dengan regresi linier dengan model: X Y 1 2 , 1 dan 2 parameternya. (6. 31)
1 dan
2 dari sebuah sampel acak dapat ditaksir ole h a dan b maka persamaan regresinya adalah bX a Y (6. 32) Untuk fonemena dua variabel bebas ( regresi non linier):
Parameter-parameternya 1,
2 dan 3 dari sebuah sampel acak dapat ditaksir oleh a, b dan c maka persamaan regresinya berupa parabola yaituc bX aX Y 2 (6. 33) 6.8 Regresi Linear
Scatter diagram (diagram pencar) adalah suatu diagram yang digunakan untuk melihat secara visual apakah ada hubungan antara 2 variabel.
Gambar 6. 1 Contoh Diagram Pencar
Sumber: http://www.spcforexcel.com/files/images/scatterpic.gif
Dengan menggunakan diagram pencar dapat dilihat apakah ada sesuatu hubungan yang berarti diantara titik-titik itu pada atau sekitar garis lurus? Jika demikian halnya, cukup alasan bagi kita untuk menduga bahwa antara variabel-variabel itu ada hubungan linear. Dalam hal lainnya, antara variabel-variabel itu diduga terdapat hubungan non linear.
Setel ah diketahui bentuk hubungan antara variabel itu, tugas selanjutnya ialah menentukan hubungan tersebut dirumuskan dalam suatu persamaan matematis. Kemudian disusun dalam suatu persamaan garis yang merepresentasikan persamaan matematisnya. Garis ini dikenal dengan nama garis regresi. Jika hubungan
itu linear, maka garis yang didapat adalahgaris regresi linear . Dalam hal lainnya didapat regresi nonlinear .Oleh karena regresi line ar merupakan bentuk regresi yang paling mudah ditelaah, kecuali itu juga karena banyak regresi nonlinear yang dapat disel esaikan dengan bantuan regresi linear, maka di
sini terutama hanyalah regresi tersebut yang akan dibicarakan.
Bagaimanakah menentukan persamaan regresi yang linear ini? Yang paling mudah ialah dengan jalan ki ra-kira menurut pengl ihatan kita. Pada kumpulan titik- titik itu ditarik sebuah garis lurus yang akan paling dekat titik-titik itu berkerumun sekitar garis yang ditarik tadi.Sesudah itu ditentukan bagaimana persamaannya.
Meskipun cara tersebut sangat mudah dilakukan namun untuk penelitian jarang dilakukan oleh karena kecuali terlalu kasar hasilnya, juga terlalu subyektif dan ini sedapat mungkin harus dihindarkan. Karenanya akan ditinjau cara yang dianggap cukup baik dan se ring digunakan. Cara yang dimaksud adalah METODA KUADRAT TERKECIL. Sebelum cara ini dibicarakan, terlebih dahulu akan ditinjau seperlunya macam-macam regresi linear yang mungkin, se hubungan dengan variabel bebas. Di atas dikatakan, bahwa jika variabel
yang diketahui terlebih dahulu dan kemudian
ditentukan berdasarkan
ini, maka ditentukan hubungan
. Rumusan hubungan ini lebih dikenal dengan nama regresi
atas
.Jika regresi
atas
ini linear, maka persamaannnya dapat dituliskan dalam bentuk linear :
(6. 34) dengan
Y = variabel tak bebas X = variabel bebas = koefi sien intercept = koefisien slope/ gradien
= error
Model tersebut ditaksir dengan :
̂
(6. 35) Dengan
̂
berarti taksiran nilai
untuk harga Y yang diketahui. Tiap pengamatan akan memenuhi : (6. 36) Sehingga error yang terjadi :(6. 37) Untuk menentukan koefisien -koefisien
dan
ini akan digunakanMetoda Kuadrat Terkecil. Ternyata bahwa untuk regresi linear, harga-harga
dan
dapat dihitung berdasarkan sekumpulan data sebanyak
buah dengan menggunakan sistem persamaan :i i a bX Y ˆ ) ( ˆ i i i i
i Y Y Y abX
1 1 2 1 1 1 i n n i i i i n n n i i i i i i Y a n b X X Y a X b X
(6. 38) Pasangan persamaan 6.38 disebut persamaan-persamaan normal untuk bentuk regresi Setelah diselesaikan, akan didapat harga-harga
dan
yang dicari dengan persamaan2 1 1 1 1 2 2 1 1 1 1 1 2 2 1 1 i i n n n n i i i i i i i i i n n i i i n n n i i i i i i i n n i i i Y X X X Y a n X X n X Y X Y b n X X
(6. 39) 6.9 Regresi Non LinearSetel ah dipelajari seperlunya mengenai bentuk hubungan linear antara dua variabel X dan Y sekarang akan diperhatikan bentuk hubungan nonlinear antar dua variabel. Tidak akan dibicarakan secara luas dan mendalam mengenai regresi nonlinear ini, tetapi hanya merupakan suatu tinjauan singkat saja, tinjauan yang pada umumnya dapat ditelaah berdasarkan teori regresi linear.
Meskipun terdapat banyak sekali bentuk regresi non linear yang biasa digunakan tetapi di sini hanyalah akan ditinjau beberapa saja yang penting dan termudah. Untuk regresi nonlinear Y atas X yang akan ditinjau di sini, antara lain berbentuk lengkungan :
a. Parabola kuadratis dengan pe rsamaan
2 Y a b X c X
(6. 40) b. Parabola kubis dengan persamaan
2 3
Y a bX cX d X
(6. 41) c. Logaritmis dengan persamaan :
b Y aX
(6. 42) d. Hiperbola dengan persamaan :
1 Y a b X (6. 43) 6.10 Regresi Linear Berganda
Ada banyak kenyataan bahwa pengamatan akan terdiri atas lebih dari dua variabel. Sehingga yang harus digunakan adalah regresi dengan variabel bebas lebih dari satu.
Contoh :
1. Harga beras tidak saja hanya ditentukan oleh adanya persediaan, tetapi juga oleh harga bensin, upah buruh dan sebagainya.
2. Produksi telur ayam tidak saja be rgantung pada banyaknya ayam petelur yang ada saja, tetapi juga dari banyak makanan yang diberikan, umur ayam dan barangkali masih ada faktor
lainnya.
Apabila ada satu variabel terikat Y dan k variabel bebas X X 1 , 2,...,X k sehingga terdapat hubungan semacam garis regresi Y atas X X 1 , 2,...,X k . Dalam bagian ini akan dijelaskan secara singkat bagaimana garis regresi yang dimaksud dapat ditentukan dan yang akan ditinjau di sini hanyalah garis regresiY atas X X 1 , 2,...,X k yang paling sederhana ialah yang dikenal dengan nama regresi linear berganda. Persamaan umum untuk regresi linear berganda ini adalah :
0 1 1 ... k k
Y a a X a X
(6. 44) Dimana a a 0 , ,. .. ,1 ak harus ditentukan dari data hasil pengamatan. Mudah dilihat bahwa regresi di atas ini merupakan perluasan dari regresi linear sederhana.
Pertanyaan yang timbul adalah bagaimana koefisien -koefisien a a 0 , ,. .. ,1 ak ditentukan ? Secara sama dengan regresi linear sederhana, maka dipergunakan Metode Kuadrat Terkecil. Oleh karena ada k+1 parameter yang harus dicari maka diperlukan k+1 persamaan. Dapat dibayangkan bahwa hal itu memerlukan metode penyelesaian yang lebih baik dan karenanya memerlukan matematika yang lebih tinggi l ebih-lebih untuk variabel yang cukup banyak.
6.11 Analisis Korelasi
Hubungan antara dua variabel
dan
yang diperoleh dinyatakan dalam bentuk persamaan matematis yang dalam statistika dikenal dengan nama garis regresi. Jika
merupakan variabel bebas dan
variabel tak bebas, regresi
atas
dapat digunakan untuk meramalkan nilai
apabila nilai
diketahui.Dalam banyak soal, jika nilai-nilai pe ngamatan terdiri atas lebi h dari sebuah variabel, bukan saja regresinya yang perlu dihitung, tetapi juga kekuatan hubungan antara variabel -variabel itu. Ukuran yang digunakan untuk itu adalah koefisien korelasi. Korelasi dapat bersifat linier atau tidak
linier. Korelasi dikatakan linier jika pada scatter diagram (diagram pencar) semua titik terlihat mengelompok disekitar garis lurus.
Untuk keperluan analisis tentang korelasi ini, seperti biasa akan dibedakan antara statistik (ialah koefisien korelasi untuk data dalam sampel) dan parameter (untuk menyatakan koefisien korelasi populasi). Koefisi en korelasi untuk sampel, jadi merupakan statistik, akan dinyatakan dengan
sedangkan parameternya dengan
(baca : rho).Dalam bagian berikut ini akan diuraikan bagaimana
dihitung dan selanjutnya akan diberikan penjelasan mengenai pengujian derajat asosiasi.6.11.1 Koefisien Korelasi
Karena ternyata korelasi dan regresi berhubungan erat, maka untuk menentukan ukuran asosiasi atau koefisien korelasi, perlu terpenuhi syarat-syarat :
1. Koefisien korelasi harus besar apabila derajat asosiasi tinggi dan harus kecil apabila derajat asosiasi rendah.
2. Koefisien korelasi harus bebas daripada satuan yang digunakan untuk mengukur variabel. Untuk mencapai kedua syarat di atas, maka untuk menentukan koefisie n korelasi r biasa digunakan statistik :
1 1 n i i i x y X X Y Y r n S S
(6. 45) Inilah rumus koefisien korelasi yang pertama yang disebut Koefisien Korelasi Person atau Product Moment.Koefisien korelasi
menunjukkan apakah cukup beralasan bagi kita untuk menyatakan ada atau tidak adanya hubungan linear antara variabel-variabel
dan
. Rumus lain yang juga sering dipergunakan adalah : 1 1 1 2 2 2 1 1 1 1 n n n i i i i i i i n n n n i i i i i i i i n X Y X Y r n X X n Y Y
(6. 46) Dengan menggunakan perhitungan matematika, ternyata dapat dibuktikan bahwa batas-batas koefisien korelasi itu berada dalam daerah / interval :-1 r 1
Tanda positif menyatakan bahwa antara variabel-variabel itu terdapat korelasi positif atau korelasi langsung yang berarti nilai variabel
yang kecil berpasangan dengan nilai variabel
yang kecil serta nilai variabel
yang besar berpasangan dengan nilai variabel
yang besar pula.Korelasi positif menunjukkan letak titik -titik dalam diagram pencar berada sekitar garis lurus yang koefi sien arahnya positif. Makin dekat letak titik- titik i tu pada garis lurus, makin kuatlah korelasi positif itu dan harganya makin dekat kepada satu.
Jika variabel
yang besar berpasangan dengan
yang kecil dan jika
kecil berpasangan dengan
yang besar, akan diperoleh Korelasi ne gatif atau korelasi invers.Dilihat dari diagram pencarnya, letak titik-titik akan berada sekitar sebuah garis lurus yang koefi sien arahnya negatif. Makin dekat letak titik -titik itu pada garis yang dimaksud, makin dekat pula nilai
kepada -1. Dan akhirnya jika titik -titik itu terletak pada garis lurus yang koefisien arahnya negatif didapat harga 1
.Dalam prakteknya jarang sekali didapatkan diagram pencar yang letak titik-titiknya pada sebuah garis lurus seperti dalam gambar 2.1 sangat jarang. Yang sering didapati adalah bentuk yang menyebabkan nilai koefisien korelasi tidak sama dengan 1 atau -1. Makin terpencar letak titik-titik itu dari sebuah garis lurus, makin dekatlah
kepada nol.Setelah dikenal apa arti koefisien korelasi, masih ada ukuran lain yang sebenarnya lebih mudah untuk ditafsirkan dalam penggunaannya. Ukuran tersebut ialah yang dinamakan koefisien determinasi yang tiada lain daripada kuadrat koefisien korelasi. Jadi :
Koefisien Determinasi = r2
(6. 47) Karena sudah diketahui bahwa koefisien korelasi berada
1
1
, maka tentulah koefisien determinasi mulai dari nol sampai dengan 1, atau :0 r2 1
Koefisien determinasi biasanya dinyatakan dengan persen. Sedangkan penafsi rannya adalah jika r = 0,94 sehingga r2 = 0,8836 atau 88,36% maka ditafsirkan sebagai 88,36% variasi suatu variabel
yang disebabkan oleh variabel lainnya.
Koefisien determinasi banyak di gunakan dalam penjelasan tambahan untuk hasil perhitungan koefisien regresi.
6.11.2 Menghitung r Untuk Data Berkelompok
Rumus-rumus 6.45 dan 6.46 adalah rumus-rumus untuk menentukan
apabila datanya masih belum disusun dalam daftar distribusi frekuensi. Rumus-rumus 6.45 dan 6.46 pula cukup menyenangkan untuk digunakan apabila datanya tidak terlalu banyak. Jika data yang sedang dicari korelasinya itu banyak sekali, dengan menggunakan rumus-rumus tersebut akan memakan waktu yang lama dari perhitungannya. Oleh karena itu perlu ada usaha untuk mempersingkatnya. Jalan yang lazim ditempuh ialah terlebi h dahulu menyusun data ke dalam daftar distribusi fr ekuensi. Oleh karena kita sedang berhadapan dengan penelitian yang terdiri atas dua variabel, maka kitapun akan memperoleh dua distribusi frekuensi. Kedua di stribusi frekuensi ini harus disajikan dalam daftar yang berklasif ikasi dua, sedemikian sehingga dampaknya banyak seperti daftar kontingensi. Banyak baris sesuai dengan banyak kelas i nterval distribusi frekuensi variabel yang satu, sedangkan banyak kolom sesuai dengan banyak kelas interval dari di stribusi frekuensi variabel kedua. Untuk variabe l yang satu, yang terdapat dalam baris, kelas-kelas intervalnya mulai dari atas ke bawah disusun seperti biasa,yakni dari data yang kecil hingga yang paling besar. Variabel yang terdapat dalam kolom, kelas -kel as intervalnya dari kiri ke kanan yang dimulai dari data yang kecil hingga yang besar.
Frekuensi data dalam daftar ini akan didapati dalam tiap-ti ap sel. Jadi frekuensi dalam setiap sel merupakan banyak data yang ada dalam kelas interval variabel yang satu dan juga yang ada dalam kelas interval variabel yang lain.
Untuk itu dipergunakan rumus berikut :
2 2 2 2 - x y x x n f uv f u f v r n f u f u n fuv f uv
(6. 48) dimana :u = koding untuk variabel X v = koding untuk variabel Y
f x = frekuensi kelas interval dari variabel X
f y = frekuensi kelas interval dari variabel Y
f = frekuensi dalam tiap sel n = banyak data.
6.11.3 Korelasi Rank
Ada kalanya ingin diketahui korelasi antara dua variabel tidak berdasarkan pada pasangan data dimana nilai sebenarnya diketahui. Umpamanya saja, kita tel ah melakukan penelitian mengenai tingkatan menyenangi merk sepatu olahraga bagi prajurit A dan prajurit B anggota TNI AL. Hasilnya dinyatakan dalam tabel di bawah ini. Untuk sepatu yang paling disukai, diberi nilai 1 dan yang paling tidak disukai diberi nil ai 10. Urut-urutan nilai tersebut dinamakan RANK. Berdasarkan rank tersebut, dapatlah ditentukan hubungan / korelasi antara keddua variabel. Ukuran yang diperoleh biasa dinamakankoefisien korelasi rankatau biasa juga dikenal dengankoefisien korelasi spearman dan disimbulkan dengan
′
(baca : er -aksen) untuk membedakan dengan koef isien korelasi yang sudah dikenal.Rumus untuk menghitung koef isien korelasi spearman adalah:
2 1 2 6 1 1 n i i d r n n
(6. 49) dengan di = selisih tiap pasang rank6.11.4 Korelasi Berganda
Korelasi be rganda merupakan korelasi dari beberapa variabel bebas secara serentak dengan variabel terikat
Misalkan ada k variabel bebas, X X 1 , 2,...,X k dan satu variabel terikatY dalam suatu persamaan regresi linear Y a a 0 1 X 1 ... a X k k maka besarnya korelasi bergandanya adalah :
1 1 1 2 2 , ,. . . , 2 ... k k k y x x a x y a x y a x y r y
(6. 50) dengan
1 1 1 2 2 2 k k k X Y x y X Y n X Y x y X Y n Y y Y n
(6. 51) 6.11.5 Korelasi ParsialKorelasi parsial adalah korelasi antara sebuah variabel tak bebas dengan sebuah variabel bebas tertentu dengan variabel -variabel bebas l ain di anggap tetap/konstan. Koefisien korelasi parsial dinyatakan dengan perumusan
Untuk dua variabel bebas :
Korelasi parsial Y dengan X1 dengan X2 dianggap konstan adalah :
1 2 1 2 1 2 1 2 2 . 2 2 1 1 YX YX YX X X YX X X X r r r r r r (6. 52) Korelasi parsial Y dengan X2 dengan X1 dianggap konstan adalah :
2 1 1 2 2 1 1 1 2 . 2 2 1 1 YX YX YX X X YX X X X r r r r r r (6. 53)Contoh soal 6.2 :
Diketahui suatu pene litian terhadap hubungan antara nilai bi aya periklanan dengan tingkat penjualan dari sebuah koperasi adalah sebagai berikut : (dalam ribuan rupiah)
No Biaya periklanan Tingkat Penjualan
1 50 40
2 51 46
3 52 44
4 53 55
5 54 49
a. Tentukan persamaan regresinya ?
b. Berapa besarnya koefisien korelasi dan koefi sien determinasinya ? c. Berapa besarnya kesalahan standar estimasinya ?
d. Bagaimana hubungan antara variabel biaya periklanan dengan tingkat penjualan? (r) e. Berapa proporsi keragaman tingkat penjualan yang dapat di jelaskan oleh biaya pe riklanan
dalam hubungan linier tersebut? (r2)
Jawab:
a. Menentukan persamaan regresinya
Langkah 1 :
Menentukan variable X dan variable Y. Dalam soal ini variable biaya periklanan merupakan variable (X) dan tingkat penjualan merupakan variable (Y).
Langkah 2:
Membuat table regresi sederhana
No X Y XY X2 Y2 1 50 40 2000 2500 1600 2 51 46 2346 2601 2116 3 52 44 2288 2704 1936 4 53 55 2915 2809 3025 5 54 49 2646 2916 2401 Total 260 234 12195 13530 11078
Langkah 3 :
Menentukan koefisien a dan koefisien b
Langkah 4:
Menentukan persamaan regresi linier sederhana Y = a + b (X)
Maka persamaan regresi dalam soal ini adalah : Y = -93,6 + 2,7 (X)
b. Menentukan koefisien korelasi dan koefi sien determinasinya.
Koefisien Korelasi