ANALISIS KEDINAMIKAN SISTEM PADA MASALAH PENJADWALAN FLOW SHOP MENGGUNAKAN ALJABAR MAX-PLUS

Seminar Nasional Matematika IV

Institut Teknologi Sepuluh Nopember, Surabaya, 13 Desember 2008

ANALISIS KEDINAMIKAN SISTEM

PADA MASALAH PENJADWALAN FLOW SHOP

MENGGUNAKAN ALJABAR MAX-PLUS

1

Nur Shofianah,

2

Subiono

1,2 _{Jurusan Matematika FMIPA Institut Teknologi Sepuluh Nopember} Jl. Arief Rahman Hakim, Kampus Keputih - Sukolilo, Surabaya 60111 – Jawa Timur

e-mail : 1_{shofianah@matematika.its.ac.id,} 2_{subiono_2003@telkomnet}

Abstrak. Dalam makalah ini dibahas aplikasi Aljabar Max-Plus pada masalah penjadwalan

flow shop, khususnya masalah pada aliran produksi permutation flow shop dengan n job 2 mesin dimana masing-masing job harus diproses tepat satu kali pada tiap mesin dengan urutan mesin yang sama. Dengan menggunakan Aljabar Max-Plus akan dikonstruksi model dinamik dari aliran flow shop yang ada. Dari model dinamik ini dapat diketahui kedinamikan sistem dan waktu periodik sistem yang tidak lain adalah nilai eigen dari matriks transisi sistem. Jika vektor eigen yang bersesuaian dengan nilai eigen ini dijadikan sebagai waktu awal tersedianya resources, maka akan terbentuk suatu jadwal yang periodik dengan periode sama dengan nilai eigen tersebut. Selain itu, jadwal yang terbentuk juga merupakan jadwal yang steady state. Selanjutnya diberikan suatu contoh kasus flow shop dengan 2 job 2 mesin untuk lebih memahami teori pada bahasan ini

.

Kata kunci: Aljabar Max-Plus, permutation flow shop, penjadwalan, steady state

1.

Pendahuluan

Aljabar Max-Plus merupakan salah satu teknik analisis pengkajian dari sistem event diskrit yang mempunyai banyak aplikasi pada teori sistem, kontrol optimal dan Petri net. Pada makalah ini, Aljabar Max-Plus akan diaplikasikan pada masalah penjadwalan produksi. Beberapa penelitian sebelumnya mengenai aplikasi Aljabar Max-Plus pada masalah penjadwalan antara lain Goto, et al (2008) menggunakan Max-Plus Linear sebagai monitoring dan metode penjadwalan untuk sistem MIMO-FIFO (Multiple Input Multiple Output – First In First Out). Bouquard et al (2006) menggunakan Aljabar Max-Plus untuk menentukan makespan dan urutan job yang optimal pada flow shop. Pada makalah ini akan dikonstruksi model dinamik sistem dari aliran produksi flow shop dengan n job 2 mesin. Istilah penjadwalan pada makalah ini mengacu pada penyusunan jadwal reguler dari waktu mulainya pemrosesan job.

Misalkan pada aliran produksi flow shop, terdapat n job yang akan dijadwalkan pada 2 mesin , dengan dan . Masing-masing job harus diproses tepat satu kali pada tiap mesin dengan urutan mesin yang sama. Permutation flow shop merupakan kelas khusus dari flow shop dimana setiap job mempunyai urutan pemrosesan yang sama pada tiap mesin. Waktu pemrosesan (processing time) job pada mesin dinotasikan dengan . Pre-emption tidak diperbolehkan dan pada suatu waktu tertentu, setiap mesin hanya dapat mengerjakan satu operasi dari satu job tertentu.

} {J_i

}

{M_k 1≤i≤n k=1,2

i k p_i,_k

Dalam makalah ini, Aljabar Max-Plus akan digunakan untuk memodelkan sistem pada aliran produksi flow shop dengan n job 2 mesin. Model tersebut diuraikan dengan menggunakan terminologi Aljabar Max-Plus. Dari model dinamik sistem dapat diketahui waktu periodik sistem ini yang tidak lain adalah nilai eigen dari matriks transisi sistem . Jika vektor eigen yang bersesuaian dengan nilia eigen ini dijadikan sebagai waktu awal tersedianya resources, maka akan terbentuk jadwal yang periodik dengan periode sama dengan nilai eigen. Jadwal tersebut tidak hanya periodik, tetapi juga merupakan jadwal yang steady state, yaitu jadwal dimana waktu putar sistem (periode), jumlah dan urutan job beserta mesin yang memproduksinya sama untuk siklus produksi selanjutnya. Informasi ini sangat berguna untuk menyusun jadwal produksi yang reguler.

2.

Aljabar Max-Plus

Alajabar Max-Plus berkaitan dengan dua operasi, maksimum (max) dan tambah (plus). Operasi tersebut mempunyai kemiripan dengan operasi perkalian biasa dua matriks, dimana pada perkalian biasa dua matriks berkenaan dengan operasi kali dan tambah. Pada perkalian biasa dua matriks, ganti kali dengan tambah dan tambah dengan maksimum maka akan diperoleh Aljabar Max-Plus. Pendekatan ini sangat sesuai bila selang waktu berperan langsung pada masalah formulasi model.

Aljabar Max-Plus dinotasikan dengan R =(Rmax,⊕,⊗,ε,e), dimana Rmax =R∪ε, dengan dan . Pada Aljabar Max-Plus, maksimum dinotasikan dengan

∞ − = def ε 0 def

e=

⊕

dan penjumlahan dinotasikan

dengan

⊗

.

ε

merupakan elemen netral terhadap

⊕

sedangkan merupakan elemen netral terhadap

. Untuk setiap berlaku dan

e

⊗

a,b∈Rmax a b max(a,b) def = ⊕ a b a b def + = ⊗

Terdapat analogi yang jelas antara Aljabar Linier dengan Aljabar Max Plus di satu sisi, juga antara teori sistem dan teori event diskret di sisi lain (Bacelli et al., 1992; Subiono, 2000). Bentuk umum dari suatu persamaan beda (aljabar biasa) adalah :

" , 2 , 1 , 0 ), ( ) 1 (k+ = Axk k= x , (1) dimana . Vektor

x

menyatakan keadaan dari model dan menyatakan keadaan saat ke-k. Sedangkan A adalah matriks berukuran n x n. Bila diberikan keadaan awal maka evolusi keadaan mendatang dari Persamaan (1) dapat ditentukan. Jika persamaan vektor pada (1) ditulis dalam bentuk persamaan skalar didapat

R a R x∈ n _ij∈ , x(k) 0 ) 0 ( x x = ) ( ) 1 ( 1 k x a k x _j n j ij i

∑

= = + ,i=1,2,...,n; k=0,1,... (2) i

x menyatakan komponen ke-i dari vektor x sedangkan adalah elemen dari matriks A. Pada Aljabar Max-Plus, operasi kali dan jumlah pada bentuk Persamaan (1) akan diubah, kali menjadi tambah dan jumlah menjadi maksimum, maka Persamaan (2) menjadi :

ij a )) ( ),..., ( ), ( max( ) 1 (k a₁ x₁ k a₂ x₂ k a x k x_i + = _i + _i + _in + _n =maxj(aij +xj) aij xj(k) (3) j ⊗ =

⊕

atau dengan notasi vektor

) ( ) 1 (k A x k x + = ⊗ , (4) dimana x Rmax,aij Rmax. Jika Persamaan (3) memenuhi keadaan awal

n ∈

∈ x(0)=x0 maka evolusi waktu

dari Persamaan (3) dapat ditentukan. Tentunya secara umum, evolusi waktu dari (2) dan (3) berbeda. Pada Persamaan (2), argumen k pada menyatakan waktu ke-k pada keadaan . Sedangkan pada Persamaan (3), argumen k bukan merupakan saat waktu tetapi menyatakan saat aktif yang ke-k. Sebagai contoh pada jaringan kerja yang terdiri dari n titik, yang diwakili oleh setiap dan berkaitan dengan garis yang terhubung dari titik j ke titik i. Titik dalam jaringan kerja dapat berperan sebagai aktivitas tertentu. Aktivitas-aktivitas ini membutuhkan waktu hingga yang disebut waktu aktivitas. Diasumsika aktivitas pada titik tertentu hanya dapat dimulai jika semua aktivitas pendahulunya sudah menyelesaikan aktivitasnya dan mengirimkan hasilnya sepanjang garis yang menghubungkan titik tersebut. Dengan demikian, menyatakan jangka waktu awal dimana titik i menjadi aktif pada saat ke-k dan adalah jumlah dari waktu aktivitas titik j dan lamanya waktu perjalanan dari titik j ke titik i. Suatu perluasan dari (4) dinyatakan dengan

) (k x x(k) i x a_ij ) (k x_i a_ij

) ( ) ( ) 1 (k A xk B u k x + = ⊗ ⊕ ⊗ y(k)=C⊗x(k) (5) dimana merupakan input dan menyatakan outputnya. Pada jaringan kerja, merupakan suatu vektor yang menunjukkan ketika sumber tertentu tersedia pada waktu ke-k sedangkan vektor merujuk pada saat dimana produk akhir dari jaringan kerja ditawarkan pada dunia luar.

) (k u y(k) u(k) ) (k y

Pada Aljabar Max-Plus, suatu bilangan λ∈R dan vektor dinamakan nilai eigen dan vektor eigen yang bersesuaian untuk suatu matriks bujur sangkar A berukuran jika memenuhi

n R x∈ max nxn v v A⊗ =λ⊗ (6) Nilai karakteristik λ dapat ditafsirkan sebagai waktu periodik dari sistem, yaitu setiap titik dari jaringan kerja yang sesuai menjadi aktif setiap λ satuan (Subiono, 2000).

3.

Konstruksi Model

Setelah memahami sistem pada aliran produksi flow shop, akan dikonstruksi suatu model dari sistem dengan menggunakan terminologi Aljabar Max-Plus. Mula-mula akan digambarkan graph berarah yang merepresentasikan aliran flow shop dimana nodes nya merupakan kombinasi antara job dengan mesin, arc

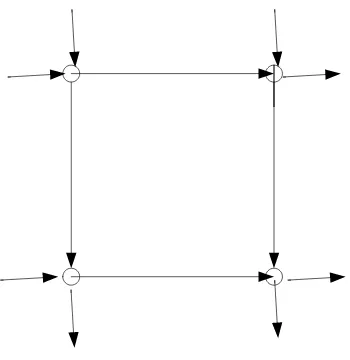
di antara nodes nya merupakan konstrain pendahulunya sedangkan bobot dari arc merupakan waktu pemrosesan yang bersesuaian. Graph berarah pada flow shop 2 job 2 mesin seperti ditunjukkan pada Gambar 1.

Gambar 1. Graph berarah pada flow shop 2 job 2 mesin

Sistem event diskrit deterministik berhingga dapat dipandang sebagai himpunan berhingga aktivitas

A (dalam hal ini aktivitas pemrosesan job) dan himpunan berhingga resourcesR . Urutan aktivitas dapat dideskripsikan dengan graph berarah . Untuk sebarang aktivitas dan , menyatakan bahwa merupakan aktivitas pendahulu bagi . Artinya, kedua aktivitas itu menggunakan resources bersama, namun tidak bisa menggunakannya pada saat yang bersamaan sehingga aktivitas harus menunggu selesainya aktivitas .

U) (A, ai aj (i,j)∈U j a a_i i a j a

Misalkan menyatakan waktu awal pemrosesan dari aktivitas dan menyatakan waktu ketika

resource

i

x a_i u_r

r tersedia. Jika (i,j)∈U, maka x_i ≥x_j + p_ji dimana adalah waktu pemrosesan aktivitas menuju aktivitas . Jika

i

merupakan aktivitas pertama untuk resource

ji p

j

a ai r maka xi ≥ur.

Misalkan merupakan himpunan aktivitas pendahulu dari aktivitas dan himpunan

resources sedemikian hingga , maka didefinisikan sebagai

) (i Γ a_i R(i) i r a₁( )= x_i A ∈ ∀a_i ⎟ (7) ⎠ ⎞ ⎜ ⎝ ⎛ ₊ = ∈ Γ ∈ i j ij rRi r j i x p u x ) ( ) ( max , ) ( max max

Misalkan yi menyatakan output, yaitu waktu ketika resources dibebaskan dari aktivitas-aktivitas

yang bersesuaian dan Φ(i) merupakan himpunan aktivitas yang bersesuaian dengan output ke-i, maka didefinisikan sebagai i y ) ( ; j i p x y_i= _j+ _ij ∈Φ (8) Pada saat ke-k, Persamaan (7) dan (8) dapat dituliskan menjadi

) ( ) ( ) (k Ax k Buk x = ⊕ (9) ) ( ) (k Cxk y = (10) dimana

[ ]

⎩ ⎨ ⎧ = j i j i k p A j ij k pendahulu proses mempunyai tidak proses jika , pendahulu proses mempunyai proses jika , ) ( ε

[ ]

⎩ ⎨ ⎧ = j i j i e B ij pendahulu proses mempunyai tidak proses jika , eksternal input mempunyai proses jika , ε

[ ]

⎩ ⎨ ⎧ = i j i j k p C j ij k eksternal output mempunyai tidak proses jika , eksternal output mempunyai proses jika , ) ( ε

Dalam hal ini, p_j(k) merupakan waktu pemrosesan aktivitas j pada saat ke-k.

Persamaan (9) merupakan persamaan implisit dalam x. Jika dilakukan substitusi secara berulang pada ruas kanan persamaan (9), akan diperoleh

(

( ) ( )

)

( ) ) (k AAx k Bu k Bu k x = ⊕ ⊕ =_A2_x(_k)⊕_ABu(_k)⊕_Bu(_k) 2 ( )

(

)

)

( ) k Bu E A k x A ⊕ ⊕ =

setelah k substitusi diperoleh

(

...

)

( ) ) ( ) ( 1 2 k Bu E A A A k x A k x = k ⊕ k− ⊕ k− ⊕ ⊕ ⊕ (11) Pada persamaan (11), E menyatakan matriks identitas, bernilai pada diagonal dan e ε untuk yang lain.

k

A menunjukkan bobot dari lintasan dengan panjang k pada graph. Karena A tidak mempunyai lintasan dengan panjang lebih besar dari n, maka untuk . Oleh karena itu, solusi dari menjadi −∞ = =ε k A k≥n

x

(

...

)

( ) ) (_{k A} 1 _A 2 _{A E Bu k} x = k− ⊕ k− ⊕ ⊕ ⊕

atau dapat dituliskan

) ( ) (_{k A}*_{Bu k} x = dengan *= ⊕ ⊕ 2⊕...⊕ n⊕ n+1⊕... (12) A A A A E A

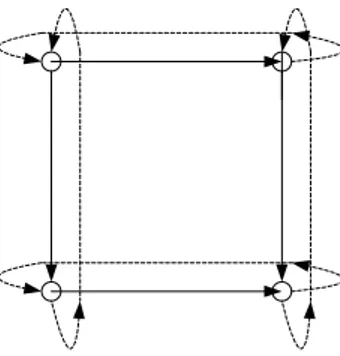
Oleh karena proses produksi ke- langsung dimulai setelah mesin menyelesaikan produksi yang dari barisan job maka akan ditambahkan feedback arc pada graph berarah seperti yang ditunjukkan pada Gambar 2. feedback arc ini digambarkan dengan garis putus-putus. Diasumsikan bahwa feedback arc mempunyai durasinol, maka

) 1 (k+ k ) 1 ( ) (k = y k−

u , dimana adalah cycle input ke-k dan cycle output ke-k, sehingga didapatkan

) (k u y(k) ) ( ) ( ) ( * k Bu CA k Cx k y = = = * ( −1) k By CA =My(k−1) (13) dengan M =CA*B merupakan matriks transisi dari

) 1 (k−

y ke . Nilai eigen dari matriks transisi ini menentukan waktu periodik sistem. Jika vektor eigen dijadikan sebagai nilai awal sistem, maka terbentuklah jadwal yang reguler.

) (k y

Gambar 2. Graph berarah dengan arc feed back pada flow shop 2 job 2 mesin

4.

Contoh Aplikasi

Contoh 1 :

Terdapat dua job dan yang akan dijadwalkan pada dua mesin dan dengan masing-masing waktu pemrosesannya sebagai berikut :

1

J J₂ M₁ M₂

Tabel 1. Waktu Pemrosesan job J₁ dan J₂ pada dua mesin M₁ dan M₂

1 J J₂ 1 M 1 4 2 M 4 1

Untuk mengkonstruksi model dari aliran produksi ini, akan digambarkan graph berarah sebagaimana ditunjukkan pada Gambar 3. Nodes tersebut merepresentasikan kombinasi job dengan mesin. Dengan demikian terdapat 4 nodes dimana masing-masing node merepresentasikan

dan . Graph berarah terdiri dari 4 nodes, 4 input dan 4 output.

) , ( ), , ( ), , (J₁ M₁ J₁ M₂ J₂ M₁ ) , (J₂ M₂

Gambar 3. Graph berarah pada flow shop 2 job 2 mesin Berdasarkan model pada persamaan (9) dan (10) diperoleh :

Bu Ax x= ⊕ Cx y= dimana ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ε ε ε ε ε ε ε ε ε ε ε ε 4 4 1 1 A ; ; ; ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ε ε ε ε ε ε ε ε ε ε ε ε e e e e B ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 4 1 4 ε ε ε ε ε ε ε ε ε ε ε ε C ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ⊕ ⊕ = e e e e A A E A 4 4 5 1 1 2 * ε ε ε ε ε ε ε

maka diperoleh ) 1 ( ) (k =My k− y

dengan M menyatakan matriks transisi, yaitu

⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⊗ ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⊗ ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = = 5 6 5 6 5 4 5 5 6 5 6 4 5 5 4 4 5 1 1 1 4 1 4 * ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε e e e e e e e e B CA M

Dengan menggunakan Scilab diperoleh λ=5 dan vektor eigen v=

[

20 21 20 21

]

t

λ dari matriks transisi M merupakan waktu periodik sistem. Agar lebih sederhana, vektor eigen tersebut dapat dituliskan menjadi . Dengan demikian, diperoleh bahwa sistem akan berulang setiap 5 satuan waktu. Jika vektor eigen dijadikan sebagai nilai awal

[

t

v= 0 1 0 1

]

(

y(0)

)

maka akan terbentuk jadwal yang reguler dari waktu selesainya pemrosesan setiap 5 satuan waktu sebagai berikut :

y(0) y(1) y(2) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 1 0 1 0 ; ; ; … ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 6 5 6 5 ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 11 10 11 10

Untuk memperoleh jadwal dari waktu awal mulainya pemrosesan job dari sistem pada aliran produksi

flow shop 2 job 2 mesin tersebut digunakan persamaan (12) sehingga dari informasi yang diperoleh mengenai nilai eigen dan vektor eigen diperoleh jadwal regular dari waktu awal mulainya pemrosesan job sebagai berikut x(1) x(2) x(3) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 5 1 1 0 ; ; ; … ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 10 6 6 5 ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 15 11 11 10

Hasil yang diperoleh ini dapat dicocokkan menggunakan Gantt Chart, yaitu bagan balok yang biasa digunakan untuk mengetahui completion time dan makespan dalam kasus penjadwalan produksi, seperti pada Gambar 4.

M1

M2

Gambar 4. Gantt Chart aliran produksi flow shop 2 job 2 mesin pada contoh 1 Contoh 2 :

Terdapat dua job dan yang akan dijadwalkan pada dua mesin dan dengan masing-masing waktu pemrosesannya sebagai berikut :

1

Tabel 2. Waktu Pemrosesan job J₁ dan J₂ pada dua mesin M₁ dan M₂ 1 J J₂ 1 M 2 3 2 M 5 6

Untuk mengkonstruksi model dari aliran produksi ini, akan digambarkan graph berarah sebagaimana ditunjukkan pada Gambar 3. Nodes tersebut merepresentasikan kombinasi job dengan mesin. Dengan demikian terdapat 4 nodes dimana masing-masing node merepresentasikan

dan . Graph berarah terdiri dari 4 nodes, 4 input dan 4 output. Berdasarkan model pada persamaan (2.10) diperoleh : ) , ( ), , ( ), , (J₁ M₁ J₁ M₂ J₂ M₁ ) , (J₂ M₂ Bu Ax x= ⊕ Cx y= dimana ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ε ε ε ε ε ε ε ε ε ε ε ε 5 3 2 2 A ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ε ε ε ε ε ε ε ε ε ε ε ε e e e e B ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 6 5 6 3 ε ε ε ε ε ε ε ε ε ε ε ε C maka diperoleh y(k)=My(k−1)

dengan M menyatakan matriks transisi, yaitu

⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = = 9 13 11 13 7 5 7 9 13 11 13 3 5 5 * ε ε B CA M

Dengan menggunakan Scilab diperoleh λ=11 dan vektor eigen v=

[

31 39 33 39

]

t. Agar lebih sederhana, vektor eigen tersebut dapat dituliskan menjadi v=

[

0 8 2 8

]

t. λ dari matriks transisi M

merupakan waktu periodik sistem. Dengan demikian, sistem akan berulang setiap 11 satuan waktu. Jika vektor eigen dijadikan sebagai nilai awal

(

y(0)

)

maka akan terbentuk jadwal yang reguler dari waktu selesainya pemrosesan setiap 11 satuan waktu sebagai berikut :

y(0) y(1) y(2) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 8 2 8 0 ; ; ; … ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 19 13 19 11 ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 30 24 30 22

Untuk memperoleh jadwal dari waktu awal mulainya pemrosesan job dari sistem pada aliran produksi

flow shop 2 job 2 mesin tersebut digunakan persamaan (12) sehingga dari informasi yang diperoleh mengenai nilai eigen dan vektor eigen diperoleh jadwal regular dari waktu awal mulainya pemrosesan job sebagai berikut x(1) x(2) x(3) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 13 8 8 2 ; ; ; … ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 24 19 19 13 ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 35 30 30 24

Hasil yang diperoleh ini dapat dicocokkan menggunakan Gantt Chart, yaitu bagan balok yang biasa digunakan untuk mengetahui waktu selesainya pemrosesan job dan makespan dalam kasus penjadwalan produksi, seperti ditunjukkan pada Gambar 5.

M1 M2

Gambar 5. Gantt Chart aliran produksi flow shop 2 job 2 mesin pada contoh 2

Pada Gambar 5 terlihat bahwa sistem akan berulang setiap 11 satuan waktu. Terlihat pada siklus produksi yang pertama, setelah memproses job 1, mesin 1 idle (pada waktu ke 4 s.d 8) padahal baik mesin 1 maupun mesin 2 masih memungkinkan untuk memproses job. Hal ini terjadi agar untuk siklus selanjutnya sistem dapat berjalan secara steady state, yaitu aliran produksi yang mempunyai waktu putar sistem (periode), jumlah dan urutan job beserta mesin yang memproduksinya sama untuk siklus selanjutnya.

5.

Kesimpulan

Aljabar Max-Plus dapat diaplikasikan pada masalah penjadwalan flow shop, khususnya masalah pada aliran produksi flow shop dengan n job 2 mesin dimana masing-masing job harus diproses tepat satu kali pada tiap mesin dengan urutan mesin yang sama. Dengan menggunakan Aljabar Max-Plus dapat dikonstruksi model dinamik dari aliran flow shop yang ada, yaitu

)

1

(

)

(

k

=

My

k

−

y

Dari model dinamik ini dapat diketahui kedinamikan sistem dan waktu periodik sistem yang tidak lain adalah nilai eigen dari matriks transisi sistem. Jika vektor eigen yang bersesuaian dengan nilai eigen ini dijadikan sebagai waktu awal tersedianya resources, maka akan terbentuk suatu jadwal yang periodik dengan periode sama dengan nilai eigen tersebut. Selain itu, jadwal yang terbentuk juga merupakan jadwal yang steady state.

Daftar Pustaka

Baccelli, F., Cohen G., Olsder G.J. dan Quadrat J.P., (1992), Synchronization and Linearity, John Wiley and Sons, New York.

Bouquard, J., -L., Lente, C., dan Billaut, J,-C., (2006), “Application of an Optimization Problem in Max-Plus Algebra to Scheduling Problems”, Discrete Applied Mathematics, 154, hal. 2064-2079 Goto, H., Masuda, S., (2008), “Monitoring and Scheduling Methods for MIMO-FIFO Systems Utilizing

Max-Plus Linear Representation”, IEMS Vol.7, No.1, pp.23-33, June, 2008.

Subiono, (2000), “Operator linear dalam Aljabar Max-Plus dan terapannya”, prosiding Seminar Nasional Matematika, Jurusan Matematika ITS, Surabaya.