Probability Statistics for Engineers Scientists
Teks penuh
Gambar
Garis besar
Dokumen terkait
One can glean from the two examples above that the sample information is made available to the analyst and, with the aid of statistical methods and elements of probability,
This exam can be taken by anyone who missed a regular exam or exams and did not qualify for or could not make it for any reason to the makeup exam given within 3 days after
A large number of practical situations can be described by the repeated per- formance of a random experiment of the following basic nature: a sequence of trials is performed so that
Probabilities associated with binomial experiments are readily obtainable from the formula b ( x ; n, p ) of the binomial distribution or from Table A.1 when n is small. In
The point and interval estimations of the mean in Sections 9.4 and 9.5 provide good information about the unknown parameter µ of a normal distribution or a nonnormal distribution
For example, if the test is two tailed and α is set at the 0.05 level of significance and the test statistic involves, say, the standard normal distribution, then a z-value is
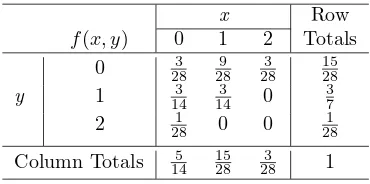
If the joint probability density function of continuous random variables Xand Yis fXYx, y, the marginal probability density functionsof Xand Yare 5-16 where Rx denotes the set of all
In an industrial example, when a sample of items selected from a batch of production is tested, the number of defective items in the sample usually can be modeled as a hypergeometric