t mtk 0707744 chapter3
Teks penuh
Gambar

Garis besar
Dokumen terkait
USAHA
Pedoman Kesesuaian Lahan Pada Komoditas Tanaman Pangan ini merupakan amanat dari Pasal 22 Peraturan Pemerintah Nomor 12 tahun 2012 tentang Insentif Perlindungan Lahan
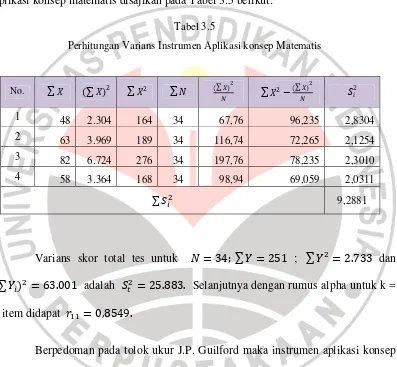
Economic Value Added (EVA) merupakan suatu alat ukur untuk mengukur kinerja keuangan yang merupakan selisih dari laba operasi bersih setelah pajak (Net operating profit after
FAKULTAS PSIKOLOGI UMM 13 dosen pembimbing magang 7 Supervisi Lapang Pembimbing lapang AP-2 Tempat magang AP- 2 Dilakukan oleh pembimbing lapang AP-2 8 Penyusunan
Pelaksanaan analisa kegiatan di bidang administrasi dan kesekretariatan serta pelaksanaan analisa dan evaluasi kegiatan di bidang administrasi umum dalam rangka pengendalian
Rata- rata nilai ketepatan yang diperoleh dari penelusuran menggunakan kata kunci bidang Ilmu Perpustakaan mendapatkan nilai ketepatan rendah yaitu sebesar Google (0,68) dan
Berdasarkan hasil penelitian, disimpulkan model pembelajaran Snowball Throwing dengan media gambar dan foto dapat meningkatkan: (1) kualitas proses pembelajaran menulis
Penelitian ini bertujuan untuk memperoleh pengetahuan yang baik mengenai (1) ada tidaknya pengaruh soft skills dengan kesiapan menjadi guru mahasiswa Pendidikan