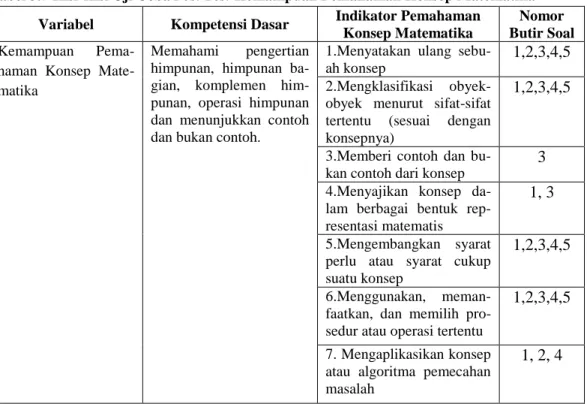
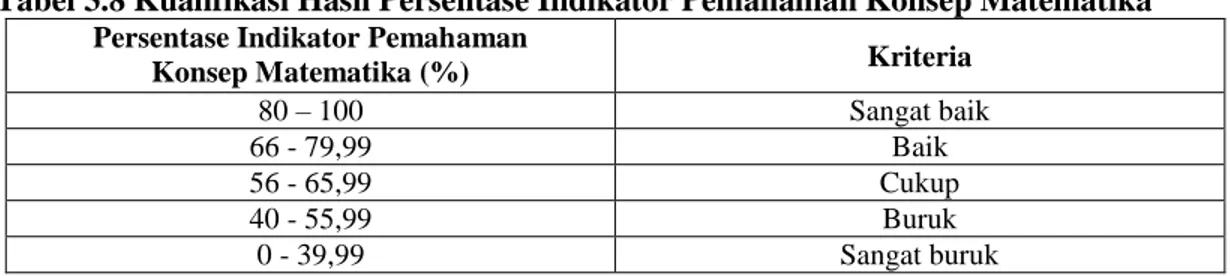
BAB III METODE PENELITIAN. suatu penelitian yang bertujuan meramalkan dan menjelaskan hal-hal yang terjadi
Teks penuh
Gambar

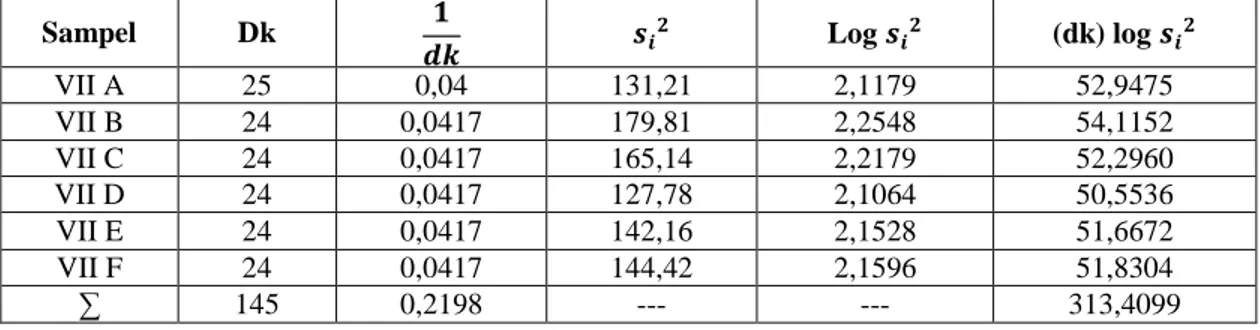
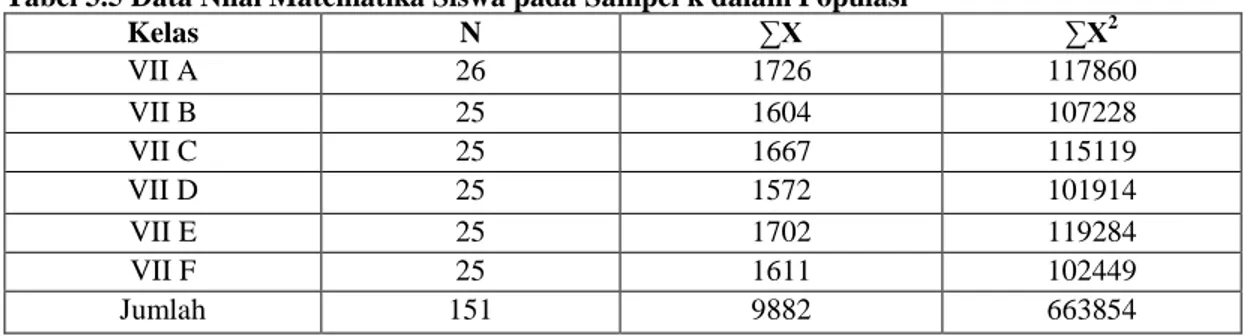

Dokumen terkait
KESATU : Menetapkan Petunjuk Teknis Pemberian Penghargaan dan Pemberian Hukuman Disiplin Bagi Pegawai Negeri Sipil di Lingkungan Sekolah Tinggi Agama Buddha Negeri Sriwijaya
Dengan demikian, kelompok memberikan kemungkinan seseorang yang secara individual memiliki kelebihan untuk melakukan kepemimpinan itu, dapat mempraktekkan dan
mikroba pada beberapa jenis antibiotika yang berbeda–beda dapat diakibatkan oleh penggunaan pada suatu jenis antibiotika dalam upaya pengobatan dan pencegahan penyakit yang
Bila ketersediaan komputer terbatas atau tidak memungkinkan dibawa ke kelas, alternatif yang dapat dilakukan adalah menggunakan Lab TIK sebagai kelas untuk mengajar sehingga team
b) Implementansi kebijakan pengurangan risiko bencana. Dimana potensi kerentanan akan lebih banyak berbicara tentang aspek teknis yang berhubungan dengan dimensi
Ho m ep ag e AR KPP Dashboard Realisasi Alat Keterangan Pelaksana DP3 Kanwil Dashboard Data Master Unit Kerja Divisi Jabatan Pegawai Wajib Pajak Jenis Dokumen
Parfum Laundry Kota Lhokseumawe Beli di Surga Pewangi Laundry HUB: 081‐3333‐00‐665 ﴾WA,TELP,SMS﴿ Beli di Toko, Agen, Distributor Surga Pewangi Laundry Terdekat/ Dikirim
Permata Niaga II No. 73 Taman Royal I Tangerang, Telp./Fax.. WAHANA TRANS UTAMA sebagai perusahaan jasa transportasi terdepan di Indonesia yang didukung dengan pengelolaan