Korelasi Umum Konstanta Henry untuk Sistem Solute Polar dalam Polimer

(1)

Korelasi Umum Konstanta Henry untuk

Sistem Solute Polar dalam Polimer

M. Arif Batutah, Gede Wibawa dan Kuswandi Jurusan Teknik Kimia, FTI. ITS Surabaya

Telp 031-5946240, Fax. 031-5999282, E-mail : gwibawa2003@yahoo.com (G.wibawa) Abstark

Dalam penelitian ini, Konstanta Henry dari solute polar dalam polimer diperoleh dari finite contrentation data VLE (vapor liquid equilibrium) dengan metode ekstrapolasi persamaan UNIQUAC pada limit konsentrasi solute mendekati nol. Hasil ektrapolasi tersebut di crosschek dengan data infinite dilution yang diperoleh dari metode inversi gas liquid chromathography (IGC) melalui hubungan linier antara ln 1/Kp dengan 1/T. Hasil yang diperoleh untuk sistem 11 solute polar dalam 4 polimer menunjukan suatu konsistensi yang baik kecuali untuk sistem acetone- polyvinyl acetate. Dari kedua metode tersebut dibuat korelasi umum, yang didasarkan pada prinsip corresponding state untuk masing-masing polimer.

Key Word : Finite Concentration, Infinite Dilution, Korelasi Umum, Konstanta Henry 1. Pendahuluan

Material polimer telah dikembangkan dalam penerapan berbagai kebutuhan, seperti kedirgantaraan, otomotif, elektronik, biomedis, perabotan rumah tangga dan lain-lain. Material-material tersebut umumnya diproses dengan melibatkan solven yang mempunyai berat molekul rendah dimana solven dan monomer yang tidak terpolimerisasi harus diambil dari produk akhir agar produk tersebut memenuhi standart kesehatan, keselamatan dan peraturan-paraturan lingkungan.

Untuk maksud tersebut pengetahuan kesetimbangan uap-cair (VLE) untuk sistem solute-polimer sangat diperlukan. Data eksperimen pada kondisi finite concentration dan infinite dilution telah di publikasikan oleh Wen, dkk. (1992a dan 1992b), namun data tersebut masih sangat terbatas. Data eksperimen sangat berguna sebagai basis dalam mengembangkan teori larutan, sehinga validitas data eksperimen sangat penting. Untuk zat-zat dengan berat molekul rendah, tes konsistensi termodinamika didasarkan pada persamaan Gibbs-Duhem, seperti tes luasan yang diusulkan oleh Herington (1951) telah digunakan secara luas untuk menguji konsistensi data eksperimen VLE sistem biner. Tetapi tes konsistensi tersebut tidak dapat diterapkan untuk VLE sistem solute-polimer, karena fase uap tidak mengandung polimer.

Untuk data VLE sistem solute-polimer, Takashima, dkk. (2003) telah mengembangkan metode validasi data eksperimen yang disebut metode crosschecking dengan memanfaatkan hubungan linier antara konstanta Henry dengan inverse temperatur, dimana sistem yang diuji validasinya adalah sistem yang mengandung solven non polar.

Pada penelitian ini metode tersebut digunakan untuk menguji validitas data eksperimen yang mengandung solute polar yaitu methanol, ethanol, propanol, 2-propanol, butanol, 2-butanol, 2 methyl-1-propanol, acetone, methyl ethyl ketone, methyl acetate dan propyl acetate dalam 4 polimer polyisoprene (PI), polyisobuthylene (PIB), poly-n-buthyl methacrylate (PBMA) dan poly vinyl acetate (PVAc). Dari data tersebut dikembangkan korelasi umum untuk masing-masing polimer.

2. Metode Ekstrapolasi

Koefesien aktifitas infinite dilution diperoleh dari ekstrapolasi data finite concentration VLE, pada konsentrasi mendekati nol menggunakan persamaan UNIQUAC yang dikemukakan oleh Abrams dan Prausnit (1975). Parameter interaksi solubilitas untuk sistem 11 solute polar dalam 4 polimer pada range temperatur 293,2 -353,2 K. telah dilaporkan oleh Wibawa, dkk (2002) dan parameter tersebut digunakan dalam penelitian ini. Koefesien aktifitas fraksi massa komponen 1 pada kondisi infinite dilution, Ω1∞ didefinisikan sebagai berikut :

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

Ω

→ ∞ 1 1 0 1 1

lim

w

a

w (1) Persamaan UNIQUAC pada kondisi tersebut ditulis :

∞ ∞ ∞ ₌ _Ω ₊ Ω C R 1 1 1 ln ln ln γ (2) dimana

(2)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = Ω ∞ 2 1 2 1 2 1 2 1 1 1 2 2 1 1 1 2 2 1 1 ln 1 ₂ ln 1 ln q r q r r q q r n q z r n r n M r M r rep rep rep C (3)

)

1 ln

(

ln

γ

1

=

1 1

−

τ

21

+

−

τ

12 ∞ rep R

_q

_n

₍₄₎

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

RT

a

_ij ij

exp

τ

(5) konstanta Henry fraksi massa dari solute, H1 di definisikan sebagai berikut :

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = → 1 1 0 1 1 lim w f H w (6) dimana f1 adalah fugasitas solute dalam Pa, selanjutnya konstanta Henry dihitung dari koefesien aktifitas pada kondisi infinite dilution dengan persamaan sebagai berikut :

L

f

H

0 1 1 1 ∞

Ω

=

(7) Pada tekanan rendah, fugasitas liquid murni dari compenen 1, f10L adalah sama pada tekanan uapnya. Definisi lain dari konstanta Henry adalah :

0 1 1

V

p

K

P

=

(8) dimana P1 adalah tekanan parsial solute dalam Pa, dan V10 adalah solubilitas solven dalam molten polimer dalam m3_{(STP)/kg polimer dan K}

p adalah konstanta Henry dalam Pa kg polimer/m3(STP). Sehingga hubungan antara kosntanta Henry H1 dan Kp adalah :

1 1

022414

.

0 M

K

H

=

p (9) dimana M1 adalah berat molekul solute.

3. Konsistensi data finite concentration dengan data infinite dilution.

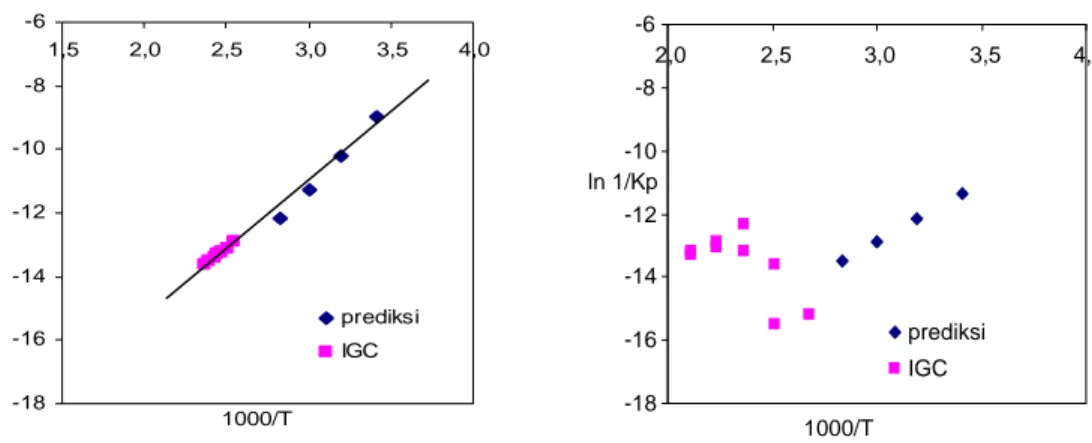
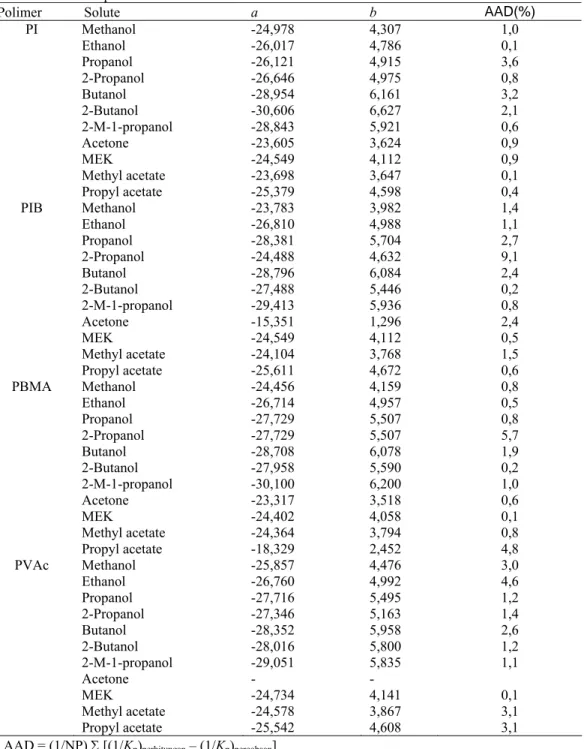
Koefesien aktifitas pada infinite dilution dari solute dalam polimer mempunyai suatu hubungan linier dalam term logaritma konstanta Henry dengan invers temperatur. Hubungan ini dapat diaplikasikan untuk membuktikan konsistensi finite consentration data VLE untuk polimer dengan data infinite dilution. Konsistensi dari hasil penelitian yang diperoleh dengan ekstrapolasi persamaan UNIQUAC di crosschek dengan data eksperimen infinite dilution yang diperoleh dari metode IGC yang telah dikonversi ke Kp melalui persamaan (9). Untuk solubilitas 11 solute polar dalam PI, PIB, PBMA dan PVAc. data infinite dilution dibandingkan dengan perhitungan solubilitas oleh persamaan UNIQUAC dalam term hubungan linier logaritma konstanta Henry dengan invers temperatur dimana kedua jenis data tersebut menunjukan adanya hubungan yang linier sebagaimana yang diilustrasikan pada Gambar (1) – (3), kecuali untuk sistem acetone-PVAc pada 373,2 -473,2 K. Analisa sulit dilakukan terhadap sistem tersebut karena error dari data IGC cukup tinggi dari satu peneliti dengan yang lain seperti ditunjukkan pada Gambar (2).

Gambar 1. konstanta Henry propanol dalam PVA Gambar 2. konstanta Henry 2 propanol dalam PVAc -18 -16 -14 -12 -10 -8 -6 2.0 2.5 3.0 3.5 4.0 1000/T ln 1 /K p prediksi IGC -18 -16 -14 -12 -10 -8 -6 1.5 2.0 2.5 3.0 3.5 4.0 1000/T ln 1 /K p prediksi IGC

(3)

Gambar 3. konstanta Henry 2 butanol dalam PVAc Gambar 4. konstanta Henry acetone dalam PVAc Konstanta Henry yang diperoleh dari data VLE pada kondisi finite consentration dan dari data infinite dilution dikorelasikan menggunakan persamaan Van’t Hoff berikut :

T b a Kp = + 1 ln (10)

dimana a dan b adalah konstanta yang tergantung dari masing-masing sistem. Hasil dari korelasi persamaan tersebut dibuat average absolute deviation (AAD) dan ditampilkan dalam tabel 2.

Tabel 1. Sumber data aktifitas pada kondisi infinite dilution

Polymer-solute T (K) NPa Reference PI Methanol 328,15 1 21 2-Propanol 328,15 1 21 Butanol 328,15 1 21 Acetone 328,15 1 21 PIB Ethanol 333,15 1 1 Ethanol 373,15 1 15 Propanol 373,15 1 15 Butanol 373,15 1 15 Acetone 373,15 1 15 Methyl acetate 373,15 1 15 Propyl acetate 373,15 1 15 PBMA Propanol 393,15 1 26 2-Propanol 373,15-473,15 5 16 Butanol 413,15 1 4 Butanol 373,15-473,15 5 57 Acetone 393,15 1 26 MEK 393,15 1 26 PVAc Methanol 373,15 1 15 Ethanol 373,15 1 15 Propanol 405,15 1 2 Propanol 393,15-423,15 7 3 Propanol 373,15 1 15 2-Propanol 398,15-413,15 2 8 2-Propanol 398,15-473,15 4 16 2-Propanol 398,15-473,15 4 14 2-Propanol 405,15 1 2 2-Propanol 393,15-423,15 7 3 2-Propanol 398,15 1 27 Butanol 398,15-473,15 4 16 Butanol 405,15 1 2 Butanol 393,15-423,15 7 3 Butanol 373,15 1 15 2-Butanol 405,15 1 2 2-Butanol 393,15-423,15 7 3 2-M-1-propanol 405,15 1 2 Acetone 398,15-473,15 4 14 -18 -16 -14 -12 -10 -8 -6 1,5 2,0 2,5 3,0 3,5 4,0 1000/T ln 1 /K p prediksi IGC 1000/T -18 -16 -14 -12 -10 -8 -6 2,0 2,5 3,0 3,5 4,0 ln 1/Kp prediksi IGC

(4)

Acetone 373,15-473,15 5 22

Acetone 373,15 1 15

Methyl acetate 373,15 1 15

Propyl acetate 373,15 1 15

4. Korelasi Umum Konstanta Henry

Korelasi umum konstanta Henry sistem solute-polimer dikembangkan dan didasarkan pada prinsip corresponding state, prinsip ini membutuhkan konstanta kritis solute. Metode ini telah dikembangkan diantaranya oleh Stiel, dkk (1985), Chiu dan Chen (1996) untuk solute non polar. Pada penelitian ini kedua metode tersebut diaplikasikan untuk solubilitas solute polar pada PI, PIB, PBMA dan PVAc.

Korelasi yang diusulkan Stiel, dkk (1985) didasarkan pada suatu analisa hasil hubungan linier antara ln (1/Kp) dengan (Tc/T)2_{yang memberikan satu intercept untuk semua solute dengan slope yang tergantung pada} faktor acentrik dari masing-masing solven.

Tabel 2 : Parameter persamaan van’t Hoff

Polimer Solute a b AAD(%)

PI Methanol -24,978 4,307 1,0 Ethanol -26,017 4,786 0,1 Propanol -26,121 4,915 3,6 2-Propanol -26,646 4,975 0,8 Butanol -28,954 6,161 3,2 2-Butanol -30,606 6,627 2,1 2-M-1-propanol -28,843 5,921 0,6 Acetone -23,605 3,624 0,9 MEK -24,549 4,112 0,9 Methyl acetate -23,698 3,647 0,1 Propyl acetate -25,379 4,598 0,4 PIB Methanol -23,783 3,982 1,4 Ethanol -26,810 4,988 1,1 Propanol -28,381 5,704 2,7 2-Propanol -24,488 4,632 9,1 Butanol -28,796 6,084 2,4 2-Butanol -27,488 5,446 0,2 2-M-1-propanol -29,413 5,936 0,8 Acetone -15,351 1,296 2,4 MEK -24,549 4,112 0,5 Methyl acetate -24,104 3,768 1,5 Propyl acetate -25,611 4,672 0,6 PBMA Methanol -24,456 4,159 0,8 Ethanol -26,714 4,957 0,5 Propanol -27,729 5,507 0,8 2-Propanol -27,729 5,507 5,7 Butanol -28,708 6,078 1,9 2-Butanol -27,958 5,590 0,2 2-M-1-propanol -30,100 6,200 1,0 Acetone -23,317 3,518 0,6 MEK -24,402 4,058 0,1 Methyl acetate -24,364 3,794 0,8 Propyl acetate -18,329 2,452 4,8 PVAc Methanol -25,857 4,476 3,0 Ethanol -26,760 4,992 4,6 Propanol -27,716 5,495 1,2 2-Propanol -27,346 5,163 1,4 Butanol -28,352 5,958 2,6 2-Butanol -28,016 5,800 1,2 2-M-1-propanol -29,051 5,835 1,1 Acetone - - MEK -24,734 4,141 0,1 Methyl acetate -24,578 3,867 3,1 Propyl acetate -25,542 4,608 3,1

(5)

2 ) ( 1 ln ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc C B A Kp ω (11)

konstanta A,B dan C ditentukan dari data eksperimen, sedangkan korelasi yang diusulkan oleh Chiu dan Chen (1996) didasarkan pada suatu analisis hubungan antara ln (1/Kp) dengan Tc/T, baik slope maupun intercept bergantung pada faktor acentrik dari masing-masing solven sebagai berikut :

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc D C B A Kp ( ) 1 ln ω ω (12)

konsatanta A, B, C, dan D diregresikan dari eksperimen untuk masing-masing polimer. Untuk PI diperoleh korelasi umum berdasarkan model Stiel (1985) :

2 ) 849 , 2 394 , 1 ( 432 , 17 1 ln ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc Kp ω (13)

dan berdasrkan model Chiu dan Chen (1996) :

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc Kp 20,160 12,776 (4,313 10,017 ) 1 ln ω ω (14)

AAD untuk masing-masing persamaan (13) dan persamaan (14) sebesar 13,5% dan 10,9%. Hasil ini menunjukkan bahwa untuk korelasi yang diusulkan chiu dan Chen (1996) lebih baik di banding dengan usulan Stiel, dkk. (1985). Korelasi umum konstanta Henry solven dalam PIB model Stiel, dkk. (1985) sebagai berikut :

2 ) 837 , 3 766 , 0 ( 704 , 18 1 ln ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc Kp ω (15)

Sedangan yang model Chiu dan Chend (1996) :

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc Kp 18,048 15,028 (3,104 11,137 ) 1 ln

ω

(16)

korelasi persamaan (16) yang mempunyai AAD 10,9% lebih baik dari pada persamaan (15) yang mempunyai AAD 13,5%. Untuk PBMA, korelasi dalam bentuk persamaan (11) dan (12), dalam penelitian ini :

2 ) 604 , 2 420 , 1 ( 823 , 18 1 ln ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc Kp ω (17) ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc Kp 20,201 9,030 (4,059 7,524 ) 1 ln ω ω (18)

AAD persamaan (17) 14,5% sedang AAD persamaan (18) sebesar 14,8% untuk masing-masing solute. Korelasi umum PVAc, analisa menunjukkan bahwa kedua korelasi baik dengan persamaan (19) maupun persamaan (20) menunjukkan AAD yang sama masing-masing 13,8%, pada korelasi ini sistem acetone-PVAc tidak diikutkan, karena tidak adanya konsistensi sewaktu di crosschek

2 ) 239 , 2 557 , 1 ( 819 , 18 1 ln ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ T Tc Kp

ω

(19)

⎟

⎠

⎞

⎜

⎝

⎛

−

+

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

T

Tc

Kp

30 ,

210

7 ,

045 (

10 ,

236

1 ,

972 )

1 ln

ω

(20)

Untuk PIB dan PBMA, AAD menunjukkan bahwa dengan korelasi persamaan (11) dan persamaan (12) tidak menunjukkan perbedaan yang signifikan seperti yang ditunjukkan pada tabel 2, sehingga PBMA dan PVc disarankan untuk menggunakan persamaan (11) karena lebih sederhana.

Tabe 3 : AAD Konstanta Henry untuk solute polar dari pers. (11) dan (12) dengan parameter yang diperoleh dari penelitian.

Polimer AAD % PI PIB PBMA PVAc 13.5 pers. (13) 18.2 pers. (15) 14.5 pers. (17) 13.8 pers. (19) 10.9 Pers. (14) 12.5 pers. (16) 14.8 pers. (18) 13.8 pers. (20)

(6)

5. Kesimpulan

Verifikasi finite concentration data VLE dengan data infinite dilution menggunakan hubungan linier antara konstanta logaritma Henry dengan invers temperatur telah berhasil diaplikasikan untuk sistem polar–polimer, kecuali untuk sistem acetone-PVAc. Sedangkan korelasi umum konstanta Henry yang diperoleh pada penelitian ini untuk masing-masing polimer PI, PIB, PBMA dan PVAc mempunyai akurasi sekitar 15% AAD.

Daftar Notasi

a konstanta persamaan (10)

a1 aktifitas solven

aij parameter interaksi persamaan UNIQUAC b konstanta persamaan (10)

fi fugasitas state untuk solven murni (Pa) H konstanta Henry fraksi massa (Pa) Kp konstanta Henry (Pa kg/m3 (STP)) Mi massa molar komponen i (kg/mol) nirep number of repeat dalam componen i pi tekanan parsial (Pa)

qi parameter luas untuk componen i ri parameter volume untuk komponen i

T temperatur (K)

Tc temperatu kristis (K) Tg temperatur transisi glass (K) Vi0 solubiltas solven (m3(STP)/kg) w fraksi massa

z coordination number (z = 10) γi koefesient aktifitas komponen i τij parameter interaksi persamaan UNIQUAC ω faktor acentrik

Ωi koefesien aktifitas fraksi massa komponen i 1 solven

2 polymer C kombinatorial R residual

∞ kondisi infinite dilution Daftar Pustaka

1. Card, T.W.; Al-Saigh, Z.Y.; Munk, P.: Macromolekul 18 (1985) 379-2435

2. Castells. R.C.; Mazza, G.D.; Arancibia, E.L. ; An. Asoc. Quim. Argent. 73 (1985) 519-530 3. Castells. R.S.; Massa, G.D.; Appl. Polym. Sci. 32 (1986) 5917-5931

4. Dipaol-Baranyi, G.; Macromolekules 14 (1981) 683-687

5. D.s. Abrams and J.M. Parusnit, “Statistical Thermodynamics of liquid Mixtures : A New Expression for the Exces Gibbs Energy of Partly or Completely Miscible Systems”, (1975) 116- 127.

6. E.F.G. Herington, J. Inst. Petrol. 37 (1951) 457-470.

7. G. Wibawa, M. Takahashi, Y. Sato, S. Takishima, H. Masuoka, “ Solubilities of 11 Polar Organic Solvents in Four Polymer Using the Piezoelectric-QuartsSorption Method’ J. Chem. Eng. Data 47 (2002) 518-524.

8. Heintz, A. ; Lichtenther, R.N.; Prausnitz, J.M.; Ber, Bunsen-Ges, Phys. Chem, 83 (1979) 926-928. 9. H. Wen, H.S. Elbro, P. Alessi, Polymer Solution Data Collection Parts 2 + 3, DECHEMA Chemistry

Data Series, DECHEMA: Frankfurt am Main, 1992.

10. J. Kim, E. Choi, K.P. Yoo and C.S. Bae, Fluid Phase Equilib., 161 (1999) 283-293. 11. K. Kojima, S. Zhang, T. Hiaki, Fluid Phase Equilib. 131 (1997) 145-179.

12. L. Durrill, R.G. Griskey, AIChE J. 15 (1969) 106-110.

13. L.I. Stiel, D.K. Chang, H.H.H. Chu, C.D. Han, J. Appl. Polym. Sci. 30 (1985) 1145-1165. 14. Liu, D.D.; Prausnitz, J.M.; J. Polym.Sci., Polym. Phys. Ed. 15 (1977) 138-142

15. Munk, P.; Du, Q.; Abdel Azim. A.A.; J. Appl. Polym.Sci., Appl. Polym. Sym. 45 (1990) 289-316 16. Newman, R.D.; Prausnit, J.M.; J. Paint. Technol. 45 (1973) 33-45

17. Prausnitz, “Molecular Thermodynamics of Fluid Phase Equiliba”, Second Edition, Prentice Hall Inc, Englewond Cliffts

(7)

19. R.M.H. Chiu, B.D.Chen Ind. Eng. Chem. Res. 35 (1996) 4386-4388

20. Rogalski, M. dan Malanowski, S. “Ebulliometers Modified for the Accurate Determination of Vapor-Equilibria” Fluid Phase Equlibria, 5, (1980) 97-112,

21. Romdhane, I. H.; Danner, R.P,; J. Chem. Eng. Data 36 (1991) 15-20 22. Sato, Y.; Inomata, H.; rai, K.; Kobunshi Robunshu 45 (1988) 287 - 289

23. Smith, Van Ness dan Abbott, “Introduction to Chemical Engeering Thermodynamics”, Fith edition, Mc Graw-Hill Companies, Inc., Singapore . (1996), 366-387,

24. S. Takishima, G. Wibawa, Y. Sato, H. Masuoka, “ A generalized correlation for Henry’s Law constans of nonpolar solutes in four polymer”, Fluid Phase Equlibria 211 (2003) 241-256.

25. S. Michaels, R.B. Parker, J. Polym. Sci. 41 (1959) 157-166 26. Wals. D.J.; McKeown, J.G.; Polymer 21 (1980) 1335-1340

27. Tseny, H.S.; Lloyd, D.R.; Ward, T.C.; Polym. Commun. 25 (1984) 262-265

28. Wisniak Jaime, “ The Herington Test for Thermodynamic Consistency”, Ind. Eng. Chem. Res, vol. 33, (1994) 177-180