Integral, Barisan Fungsi, Pertukaran Limit dan Integral

Integral, Barisan Fungsi, Pertukaran Limit dan Integral

12. LUAS DAERAH DAN INTEGRAL

12.1 Luas Daerah di Bawah Kurva

Masalah menentukan luas daerah (dan volume ruang) telah dipelajari sejak era Pythagoras dan Zeno, pada tahun 500-an SM. Konsep integral (yang terkait erat dengan luas daerah) berpijak pada metode ‘exhaustion’, yang telah dipakai oleh Plato dan Eudoxus, dan kemudian oleh Euclid dan Archimedes, untuk menghitung luas daerah lingkaran.

Pada 1630-an, Pierre de Fermat tertarik untuk menghitung luas daerah di bawah kurva. Misalkanf kontinu pada interval [a, b]. Apakah masuk akal untuk membahas ‘luas’ daerah di bawah kurvay=f(x)? Jika ya, bagaimanakah kita menghitungnya?

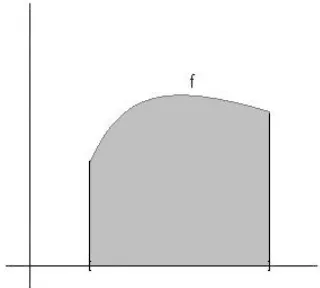
Gambar 12.1_{Daerah di bawah kurvay=f(x)}

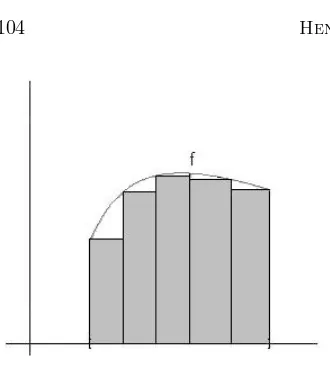
Gambar 12.2_{Luas daerahL}

Misalkan L menyatakan himpunan semua bilangan L yang dapat diperoleh sebagai jumlah luas daerah persegi-panjang kecil sebagaimana dalam Gambar 12.2. Maka ‘luas daerah’ di bawah kurva y = f(x) mestilah lebih besar daripada setiap anggota L. Tampaknya masuk akal untuk mendefinisikan ‘luas daerah’ di bawah kurvay=f(x) sebagai bilangan terkecil yang lebih besar daripada setiap anggotaL, yakni supL.

Contoh 1. Misalkan f(x) = x2_{, x ∈ [0,1]. Maka, dengan membagi interval [0,1]} atasninterval bagian yang sama panjang dan menghitung jumlah luas daerah persegi-panjang yang terbentuk, luas daerah di bawah kurva y =f(x) mestilah lebih besar daripada

1 n

h

0 + 1 2 n2 +

22

n2 +· · ·+

(n−1)2 n2

i

.

Jumlah deret ini sama dengan

(n−1)n(2n−1) 6n3 . Mengingat (n−1)n(2n_6n3 −1) ≤1₃ untuk tiapn∈Ndan

(n−1)n(2n−1)

6n3 →

1 3

untuk n→ ∞, maka bilangan terkecil yang lebih besar daripada (n−1)n(2n_6n3 −1) untuk

tiapn∈Nadalah 1

Soal Latihan

1. Buktikan bahwa (n−1)n(2n_6n3 −1) ≤ 1₃ untuk tiap n ∈ N, dan simpulkan bahwa

sup n∈N

(n−1)n(2n−1) 6n3 = 1₃.

2. Tentukan luas daerah di bawah kurva y= 1 +x, x∈[0,1], dengan cara seperti pada Contoh 1. Apakah hasil yang diperoleh sesuai dengan pengetahuan ge-ometri kita?

12.2 Integral

Misalkan f kontinu pada interval [a, b]. Definisikan partisi dari [a, b] sebagai himpunanP :={x0, x1, . . . , xn}dengan

a=x0< x1<· · ·< xn−1< xn=b.

Karena f kontinu pada [a, b], maka f terbatas pada [a, b]. Jadi, diberikan sembarang partisiP :={x0, x1, . . . , xn} dari [a, b], kita dapat mendefinisikan

mk:= inf xk−1≤x≤xk

f(x),

untukk= 1,2, . . . , n. Dengan demikian, untuk tiap partisiP, kita dapat membentuk deret

L(P, f) := n

X

k=1

mk(xk−xk−1).

(Buatlah suatu ilustrasi yang menyatakan nilaiL(P, f).) Misalkanf terbatas di atas pada [a, b], katakanlah

f(x)≤M, x∈[a, b]. Maka

L(P, f)≤M n

X

k=1

(xk−xk−1) =M(b−a).

Sekarang kita sampai pada definisi integral. Jikaf kontinu pada interval [a, b], maka kita definisikanintegraldarif pada [a, b] sebagai

Z b

a

f(x)dx:= sup P

L(P, f),

dengan nilai supremum diambil atassemuapartisiP dari [a, b]. Dalam half(x)≥0 untuk setiapx∈[a, b], maka Rb

af(x)dx dapat diinterpre-tasikan sebagai luas daerah di bawah kurvay=f(x).

Sebagai tambahan, jikaa < b, maka kita definisikan

Z a Selain itu, untuk sembaranga∈R, kita definisikan

Z a

Catatan_{. Bukti Proposisi 3 agak panjang; lihat [2].} Soal Latihan

1. Buktikan Proposisi 2. 2. Buktikan bahwa Rb

ac dx=c(b−a).

3. Diketahui f(x) =x, x∈[a, b]. Buktikan bahwa L(P, f)≤1

untuk sebarang partisiP dari [a, b]. Selanjutnya, dengan menggunakan definisi integral, buktikan bahwa

Z b

a

f(x)dx=1 2(b

2_−a2_).

12.3 Turunan dari Integral; Teorema Dasar Kalkulus

Misalkanf terdefinisi pada (a, b). Misalkan F kontinu pada [a, b] dan mempu-nyai turunan pada (a, b) dengan

F′_{(x) =f(x)}

untuk tiapx∈(a, b). MakaF disebut sebagaianti turunandarif pada [a, b].

Contoh 4. Jika f(x) =x3_{, maka fungsiF yang didefinisikan sebagai} F(x) =1

4x 4_{+ 5}

merupakan suatu anti turunan dari f. Secara umum, fungsi G yang didefinisikan sebagai

G(x) =1 4x

4_+C, dengan Ckonstanta, merupakan anti turunan darif.

Pembaca mungkin bertanya: apa urusannya anti turunan dengan integral? Un-tuk menjawab pertanyaan ini, misalkan f kontinu pada [a, b]. Definisikan F pada [a, b] sebagai

F(x) :=

Z x

a

f(t)dt, x∈[a, b].

Dalam teorema berikut, kita akan menunjukkan bahwaF merupakan suatu anti tu-runan darif pada [a, b].

Teorema 5 (Teorema Dasar Kalkulus I).Misalkan f kontinu pada [a, b] danF

didefinisikan pada[a, b] sebagai

F(x) :=

Z x

a

Maka, F merupakan suatu anti turunan dari f pada [a, b]; yakni, F kontinu pada

[a, b], mempunyai turunan pada (a, b), danF′_{(x) =f(x)untuk tiap x∈(a, b).}

Bukti. Karenaf kontinu pada [a, b], makaf terbatas pada [a, b], katakanlah |f(t)| ≤κ

untuk tiapt∈[a, b]. Selanjutnya, untukx, c∈[a, b], kita mempunyai

F(x)−F(c) =

Z x

c

f(t)dt, sehingga

|F(x)−F(c)| ≤κ|x−c|. JadiF kontinu pada [a, b].

Selanjutnya perhatikan bahwa untukx6=ckita mempunyai F(x)−F(c)

x−c −f(c) = 1 x−c

Z x

c

[f(t)−f(c)]dt. Karena f kontinu di c, kita dapat memilihδ >0 sedemikian sehingga

F(x)−F(c) x−c −f(c)

< ǫ,

untuk 0<|x−c|< δ. Ini menunjukkan bahwaF′_{(c) =f(c), dan ini berlaku untuk} setiapc∈[a, b].

Teorema 6 (Teorema Dasar Kalkulus II). Setiap fungsi f yang kontinu pada

[a, b] mempunyai anti turunan pada [a, b]. Jika G adalah anti turunan dari f pada

[a, b], maka

Z b

a

f(t)dt=G(b)−G(a).

Bukti. Definisikan fungsiF pada [a, b] sebagai

F(x) :=

Z x

a

f(t)dt, x∈[a, b]. Maka,F merupakan suatu anti turunan darif pada [a, b], dan

Z b

a

Sekarang, jikaGadalah anti turunan darif pada [a, b], maka G(x) =F(x) +C, x∈[a, b], suatu konstantaC. Karena itu,

Z b

a

f(t)dt= [F(b) +C]−[F(a) +C] =G(b)−G(a), sebagaimana yang kita harapkan.

Soal Latihan

1. Buktikan bahwa R1

0 x 2_dx= 1

3.

2. Misalkan r∈Q, r6=−1. Buktikan bahwaR1

0 x

r_dx= 1 r+1.

3. Misalkanf dangkontinu pada [a, b]. Buktikan, dengan menggunakan Teorema Dasar Kalkulus II, bahwa untuk setiapλ, µ∈R, berlaku

Z b

a

[λf(x) +µg(x)]dx=λ

Z b

a

f(x)dx+µ

Z b

a

g(x)dx.

4. Misalkanf dangkontinu pada [a, b]. Buktikan Ketaksamaan Cauchy-Schwarz:

hZ b

a

f(x)g(x)dxi 2

≤

Z b

a

[f(x)]2dx·

Z b

a

13. INTEGRAL RIEMANN

13.1 Jumlah Riemann Atas dan Jumlah Riemann Bawah

Pada Bab 12 kita mengasumsikan bahwaf kontinu pada [a, b] dan mendefini-sikan integralRb

af(x)dxsebagai supremum dari himpunan semua jumlah luas daerah persegi-panjang kecil di bawah kurva y = f(x). Sesungguhnya, kita dapat pula mendefinisikan integralRb

af(x)dxsebagai infimum dari himpunan semua jumlah luas daerah persegi-panjang kecil ‘di atas’ kurvay=f(x). Dalam half kontinu pada [a, b], kedua definisi tersebut akan menghasilkan nilai yang sama.

Pada bab ini, kita akan memperluas definisi integral untuk fungsif : [a, b]→R

yang terbatas, sebagaimana yang dilakukan oleh Bernhard Riemann pada 1850-an. Seperti pada Sub-bab 12.2, diberikan sembarang partisiP :={x0, x1, . . . , xn} dari [a, b], kita dapat mendefinisikan

L(P, f) := n

X

k=1

mk(xk−xk−1).

dengan mk:= inf xk−1≤x≤xk

f(x), k= 1,2, . . . , n.Pada saat yang sama, kita juga dapat mendefinisikan

U(P, f) := n

X

k=1

Mk(xk−xk−1).

dengan Mk := sup xk−1≤x≤xk

f(x), k= 1,2, . . . , n.

L(P, f) dan U(P, f) disebut sebagai jumlah Riemann bawah dan jumlah Rie-mann atasdarif yang berkaitan dengan partisiP. Perhatikan bahwa

Selanjutnya, jikaP :={x0, x1, . . . , xn}danQ:={y0, y1, . . . , ym}adalah partisi dari [a, b], makaQdisebut sebagai suatuperhalusandariP apabila setiap titik partisi xk∈P merupakan titik partisi diQ, yakniP ⊆Q. Dalam hal ini, setiap sub-interval yang terkait dengan partisiP dapat dinyatakan sebagai gabungan dari beberapa sub-interval yang terkait dengan partisiQ, yakni

[xk−1, xk] = [yi−1, yi]∪[yi, yi+1]∪ · · · ∪[yj−1, yj].

Catat bahwa kita dapat memperoleh suatu perhalusan dari sembarang partisiP de-ngan menambahkan sejumlah titik keP.

Proposisi 1. Jika Q merupakan perhalusan dari P, maka L(P, f) ≤ L(Q, f) dan

U(Q, f)≤U(P, f).

Akibat 2. JikaP1 danP2 adalah dua partisi sembarang dari[a, b], makaL(P1, f)≤ U(P2, f).

Soal Latihan

1. Buktikan Proposisi 1. (Petunjuk. Mulai dengan kasus Q =P ∪ {x∗_{} dengan} x∗_∈/P.)

2. Buktikan Akibat 2.

13.2 Integral Riemann

Seperti pada sub-bab 13.1, pada sub-bab ini kita mengasumsikan bahwa f : [a, b] → R terbatas. Menurut Akibat 2, himpunan {L(P, f) : P partisi dari [a, b]} terbatas di atas (oleh suatu jumlah Riemann atas), sementara himpunan{U(P, f) : P partisi dari [a, b]}terbatas di bawah (oleh suatu jumlah Riemann bawah). Karena itu kita dapat mendefinisikan

L(f) := sup{L(P, f) : P partisi dari [a, b]} dan

L(f) disebut sebagaiintegral Riemann atas darif, sementara U(f) disebut sebagai

integral Riemann bawahdarif.

Proposisi 3. L(f)≤U(f).

Bukti. Untuk setiap partisiP0dari [a, b],U(P0, f) merupakan batas atas dari{L(P, f) : P partisi dari [a, b]}, sehingga

L(f) = sup{L(P, f) : P partisi dari [a, b]} ≤U(P0, f).

Karena ini berlaku untuk sembarang partisiP0, makaL(f) merupakan batas bawah dari{U(P0, f) : P0partisi dari [a, b]}. Akibatnya

L(f)≤inf{U(P0, f) : P0partisi dari [a, b]}=U(f), sebagaimana yang diharapkan.

Secara umum, L(f)6=U(f). Sebagai contoh, jikaf : [0,1]→R didefinisikan sebagai

f(x) =

0, xrasional; 1, xirasional, maka L(f) = 0 sementara U(f) = 1.

Jika L(f) = U(f), maka f dikatakan terintegralkan Riemann dan nilai yang sama tersebut didefinisikan sebagai integral Riemann dari f pada [a, b], yang di-lambangkan denganRb

a f(x)dx. (Seperti pada Bab 12, kita definisikan

Ra

b f(x)dx= −Rb

a f(x)dx dan

Ra

a f(x)dx= 0.)

Sebagai contoh, jika f bernilai konstan pada [a, b], katakan f(x) = c untuk setiap x ∈ [a, b], maka L(f) = U(f) = c(b −a) dan karenanya f terintegralkan Riemann pada [a, b] dengan

Z b

a

f(x)dx=c(b−a).

Teorema berikut memberikan suatu kriteria untuk keterintegralanf pada [a, b]. (Untuk selanjutnya, ‘terintegralkan’ berarti ‘terintegralkan Riemann’ dan ‘integral’ berarti ‘integral Riemann’.)

Teorema 6. f terintegralkan pada [a, b] jika dan hanya jika untuk setiap ǫ > 0

Bukti. Misalkan f terintegralkan pada [a, b]. Ambil ǫ > 0 sembarang. Dari definisi supremum, terdapat suatu partisiP1dari [a, b] sehingga

L(f)−ǫ

2 < L(P1, f).

Dari definisi infimum, terdapat pula suatu partisiP2 dari [a, b] sehingga U(P2, f)< U(f)−

ǫ 2.

Sekarang misalkan Pǫ =P1∪P2. Maka Pǫ merupakan perhalusan dari P1 dan P2. Akibatnya,

L(f)−ǫ

2 < L(P1, f)≤L(Pǫ, f)≤U(Pǫ, f)≤U(P2, f)< U(f) + ǫ 2. NamunL(f) =U(f), sehingga kita peroleh

U(Pǫ, f)−L(Pǫ, f)< ǫ.

Sebaliknya misalkan untuk setiap ǫ > 0 terdapat suatu partisi Pǫ dari [a, b] sedemikian sehingga

U(Pǫ, f)−L(Pǫ, f)< ǫ. Maka, untuk setiapǫ >0, berlaku

0≤U(f)−L(f)≤U(Pǫ, f)−L(Pǫ, f)< ǫ.

Dari sini kita simpulkan bahwaU(f) =L(f) atauf terintegralkan pada [a, b].

Akibat 7. Misalkan terdapat barisan partisi hPnidari [a, b]sedemikian sehingga lim

n→∞[U(Pn, f)−L(P n, f)] = 0.

Makaf terintegralkan pada [a, b]dan

lim

n→∞L(Pn, f) =

Z b

a

f(x)dx= lim

n→∞U(Pn, f).

Soal Latihan

2. Misalkan f(x) = x, x ∈ [0,1], dan Pn = {0,_n1,_n2, . . . ,1}, n ∈ N. Tunjukkan bahwa lim

n→∞[U(Pn, f)−L(Pn, f)] = 0, dan kemudian simpulkan bahwaf terin-tegralkan pada [0,1].

3. Misalkan fungsif didefinisikan pada [0,1] sebagai

f(x) =

0, 0≤x <1; 1, x= 1.

Buktikan bahwaf terintegralkan pada [0,1] denganR1

0 f(x)dx= 0. 4. Misalkan fungsif didefinisikan pada [0,2] sebagai

f(x) =

1, 0≤x≤1; 2, 1< x≤2. Buktikan bahwaf terintegralkan pada [0,2] denganR2

0 f(x)dx= 3.

13.3 Keterintegralan Fungsi Kontinu dan Fungsi Monoton

Sebagaimana disinggung pada awal bab ini, fungsi yang kontinu pasti terinte-gralkan.

Teorema 8. Jikaf kontinu pada [a, b], maka f terintegralkan pada[a, b].

Bukti. Menurut Teorema 18 pada Bab 8, fungsi yang kontinu pada [a, b] mestilah kontinu seragam pada [a, b]. Karena itu, diberikanǫ >0 sembarang, terdapat δ >0 sedemikian sehingga untukx, y∈[a, b] dengan|x−y|< δ berlaku

|f(x)−f(y)|< ǫ b−a.

Selanjutnya, untuk tiapn∈Ndengan n > b−a

δ , tinjau partisiPn :={x0, x1, . . . , xn} dengan xk =a+k· b−_na, k = 0,1, . . . , n. (Di sini, interval [a, b] terbagi menjadin sub-interval sama panjang.)

Menurut Teorema 13 pada Bab 8, pada setiap sub-interval [xk−1, xk],f menca-pai nilai maksimumMk dan minimummk, katakanlah

Dalam hal ini kita peroleh Dari sini kita simpulkan bahwa lim

n→∞[U(Pn, f)−L(Pn, f)] = 0, dan karenanya f terintegralkan pada [a, b].

Selain fungsi kontinu, teorema berikut menyatakan bahwa fungsi monoton juga terintegralkan.

Teorema 9. Jikaf monoton pada [a, b], maka f terintegralkan pada[a, b].

Bukti. Tanpa mengurangi keumuman, asumsikan f naik pada [a, b]. Untuk tiap n∈N, tinjau partisiPn:={x0, x1, . . . , xn}dengan xk =a+k·b−na, k= 0,1, . . . , n. Karena f naik pada [xk−1, xk], makamk =f(xk−1) danMk =f(xk). Dalam hal ini kita peroleh suatu deret teleskopis

n

Dengan demikianf mestilah terintegralkan pada [a, b].

Soal Latihan

1. Misalkan f : [a, b]→Rkontinu dan f(x)≥0 untuk setiapx∈[a, b]. Buktikan jikaL(f) = 0, makaf(x) = 0 untuk setiapx∈[a, b].

2. Misalkanf : [a, b]→Rkontinu dan, untuk setiap fungsig: [a, b]→Ryang terin-tegralkan,f gterintegralkan danRb

14. SIFAT-SIFAT INTEGRAL RIEMANN

14.1 Sifat-sifat Dasar Integral Riemann

Pada bab ini kita akan mempelajari sifat-sifat dasar integral Riemann. Sifat pertama adalah sifat kelinearan, yang dinyatakan dalam Proposisi 1. Sepanjang bab ini,I menyatakan interval [a, b], kecuali bila kita nyatakan lain.

Proposisi 1. Misalkanf, g:I→Rterintegralkan padaI, danc∈Rsuatu konstanta. Makacf danf+g terintegralkan padaI dan

Z b

a

cf(x)dx=c

Z b

a

f(x)dx, (1)

Z b

a

(f+g)(x)dx=

Z b

a

f(x)dx+

Z b

a

g(x)dx. (2)

Bukti. (1) Jika c = 0, maka pernyataan tentang cf jelas benar. Sekarang tinjau kasus c >0. (Kasus c <0 serupa dan diserahkan sebagai latihan). Misalkan P := {x0, x1, . . . , xn}partisi sembarang dariI. Karenac >0, kita mempunyai

inf{cf(x) : x∈[xk−1, xk]}=cinf{f(x) : x∈[xk−1, xk]}

untuk k= 1,2, . . . , n. Kalikan tiap suku ini denganxk−xk−1 dan jumlahkan, kita dapatkan

L(P, cf) =cL(P, f). Jadi, karenac >0, kita peroleh

L(cf) = sup{cL(P, f) : Ppartisi dariI}=csup{L(P, f) : Ppartisi dariI}=cL(f). Dengan cara yang serupa kita peroleh pulaU(P, cf) =cU(P, f) dan

Karena f terintegralkan,U(f) =L(f) dan akibatnya

untuk sembarang partisi P dari I. Sekarang, jika ǫ > 0 diberikan, maka terdapat partisiPf,ǫ danPg,ǫsedemikian sehingga

U(Pf,ǫ, f)≤L(Pf,ǫ, f) + Menurut Kriteria Keterintegralan Riemann,f +gterintegralkan.

Selanjutnya perhatikan bahwa dari ketaksamaan di atas, kita peroleh

Dari kedua ketaksamaan ini, kita peroleh

Karena ini berlaku untukǫ >0 sembarang, kita simpulkan bahwa

Z b

Proposisi berikut dikenal sebagai sifat kepositifan integral Riemann. (Buktinya diserahkan sebagai latihan.)

Catatan_{. Bukti Proposisi 4 tidak dibahas di sini; lihat [1] bila ingin mempelajarinya.} Soal Latihan

1. Buktikan Proposisi 1 bagian (1) untuk kasusc <0. 2. Buktikan Proposisi 2 dan Akibat 3.

4. Buktikan jika f terintegralkan padaI dan |f(x)| ≤K untuk tiap x∈I, maka

Rb

af(x)dx

≤K|b−a|.

14.2 Teorema Dasar Kalkulus untuk Integral Riemann

Analog dengan Teorema Dasar Kalkulus I (Teorema 5 pada Sub-bab 12.3) untuk integral dari fungsi kontinu, kita mempunyai hasil berikut untuk integral Riemann dari fungsi terbatas.

Teorema 5 (Teorema Dasar Kalkulus I).Misalkanf terbatas padaI= [a, b]dan

F didefinisikan padaI sebagai

F(x) :=

Z x

a

f(t)dt, x∈I.

Maka,F kontinu padaI. Selanjutnya, jikaf kontinu dic∈(a, b), maka F mempun-yai turunan di cdanF′_{(c) =f(c).}

Demikian pula kita mempunyai Teorema Dasar Kalkulus II untuk integral Riemann, yang dapat dibuktikan tanpa menggunakan Teorema Dasar Kalkulus I melainkan dengan menggunakan Kriteria Keterintegralan Riemann.

Teorema 6 (Teorema Dasar Kalkulus II). Misalkan f terintegralkan pada I = [a, b]. Jika F :I→Radalah anti-turunan darif padaI, maka

Z b

a

f(t)dt=F(b)−F(a).

Bukti. Diberikanǫ >0 sembarang, pilih partisiP :={x0, x1, . . . , xn}dariIsedemikian sehingga

U(P, f)−L(P, f)< ǫ.

Menurut Teorema Nilai Rata-rata (yang kita terapkan pada F), pada tiap interval [xk−1, xk] terdapat titiktk ∈(xk−1, xk) sedemikian sehingga

F(xk)−F(xk−1) = (xk−xk−1)f(tk).

untuk tiapk= 1,2, . . . , n. Perhatikan bahwa bila kita jumlahkan suku-suku di tengah, maka kita peroleh suatu deret teleskopis yang jumlahnya sama denganF(b)−F(a). Karena itu, kita peroleh

L(P, f)≤F(b)−F(a)≤U(P, f). Namun, kita juga mempunyai

L(P, f)≤

Z b

a

f(t)dt≤U(P, f). Akibatnya, kita peroleh

Z b

a

f(t)dt−[F(b)−F(a)] < ǫ.

Karena ini berlaku untukǫ >0 sembarang, kita simpulkan bahwa

Z b

a

f(t)dt=F(b)−F(a), sebagaimana yang kita kehendaki.

Soal Latihan

1. Misalkan f(x) =|x|, x∈[−1,1]. Terkait denganf, definisikan F(x) :=

Z x

−1

f(t)dt, x∈[−1,1]. (a) Peroleh rumus untukF(x), x∈[−1,1].

(b) Periksa bahwaF′_{(x) =f(x) untukx∈[−1,1].} (c) Periksa bahwaR1

−1f(t)dt=F(1)−F(−1). 2. Misalkan f : [−1,1]→Rdidefinisikan sebagai

f(x) =

 



−1, −1≤x <0; 0, x= 0; 1, 0< x≤1, Terkait denganf, definisikan

F(x) :=

Z x

1

(a) Peroleh rumus untukF(x). ApakahF kontinu pada [−1,1]? (b) Tunjukkan bahwaF′_{(x) =f(x) untukx∈[−1,1], x6= 0.}

(c) Periksa apakahR1

−1f(t)dt=F(1)−F(−1). Berikan argumen yang men-dukung fakta tersebut.

3. Misalkan f dan g terintegralkan dan mempunyai anti- turunan F danGpada I= [a, b]. Buktikan bahwa

(Catatan_{. Hasil ini dikenal sebagaiteknik pengintegralan parsial.)}

14.3 Teorema Nilai Rata-rata dan Teorema Taylor untuk Integral

Jikaf kontinu padaI= [a, b], maka (menurut Teorema 9 pada Bab 8) f akan mencapai nilai maksimumM dan minimummpada [a, b]. Menurut Proposisi 3, kita mempunyai

af(x)dxdisebut sebagainilai rata-rata integralf pada intervalI. (Dalam versi diskrit, nilai rata-rata aritmetik dari sejumlah bilangan adalah jumlah dari bilangan-bilangan tersebut dibagi dengan banyaknya bilangan itu. Dalam versi ‘kon-tinum’, integral menggantikan jumlah dan panjang interval menggantikan banyaknya bilangan.)

Mengingat m dan M ada di daerah nilai f dan 1 b−a

Rb

af(x)dx ada di antara kedua nilai tersebut, maka menurut Teorema Nilai Antara mestilah terdapat suatu titikc∈Isedemikian sehingga

f(c) = 1 b−a

Z b

a

Fakta ini dikenal sebagaiTeorema Nilai Rata-ratauntuk integral, yang dinyatakan di bawah ini. (Ingat bahwa sebelumnya kita juga mempunyai Teorema Nilai Rata-rata untuk turunan. Dalam konteks turunan, nilai rata-rata analog dengan ‘kecepatan rata-rata’ dalam fisika.)

Teorema 7 (Teorema Nilai Rata-rata untuk Integral). Jika f kontinu pada

I= [a, b], maka terdapatc∈I sedemikian sehingga

Pada Bab 10, kita telah membahas Teorema Taylor untuk turunan. Sekarang kita akan membahas teorema yang serupa untuk integral.

Teorema 8 (Teorema Taylor untuk Integral). Misalkan f, f′_{, . . . , f}(n) _kontinu

Bukti. Dengan pengintegralan parsial, kita peroleh

En=

Jika kita lakukan pengintegralan parsial hinggan kali, maka kita akan sampai pada hasil di atas.

Soal Latihan

1. Buktikan jika f kontinu pada I = [a, b] danf(x)≥0 untuk tiapx∈I, maka terdapatc∈I sedemikian sehingga

f(c) =h 1 b−a

Z b

a

2. Buktikan jika f kontinu pada I = [a, b] danf(x)≥0 untuk tiapx∈I, maka untuk sembarangk∈Nterdapatc=ck∈Isedemikian sehingga

f(c) =h 1 b−a

Z b

a

fk(x)dxi1/k.

3. Misalkanf dangadalah fungsi yang kontinu padaI= [a, b] sedemikian sehingga

Z b

a

f(x)dx=

Z b

a

g(x)dx.

15. INTEGRAL SEBAGAI LIMIT

15.1 Jumlah Riemann

Dalam kuliah Kalkulus pada tahun pertama, integral Riemann biasanya diperke-nalkan sebagai limit dari ‘jumlah Riemann’, tidak melalui integral Riemann atas dan integral Riemann bawah. Hal ini memang dimungkinkan, karena nilai limit dari jum-lah Riemann tersebut sama dengan integral Riemann yang kita bahas pada Bab 13.

Seperti pada bab sebelumnya, sepanjang bab iniI menyatakan interval [a, b], kecuali bila kita nyatakan lain. Misalkanf :I→Rterbatas danP :={x0, x1, . . . , xn} partisi dari I. Jika tk adalah bilangan sedemikian sehingga xk−1 ≤ tk ≤ xk untuk k= 1,2, . . . , n, maka jumlah

S(P, f) := n

X

k=1

f(tk)(xk−xk−1)

disebut sebagai suatu jumlah Riemann untuk f, yang terkait dengan partisiP dan

titik-titik sampeltk.

Catat bahwa untuk sebuah partisi P terdapat tak terhitung banyaknya cara memilih titik-titik sampeltk, dan karenanya terdapat tak terhitung banyaknya jumlah Riemann yang terkait dengan partisiP.

Untuk fungsif ≥0 pada I, jumlah Riemann dapat diinterpretasikan sebagai jumlah luas daerah persegipanjang dengan lebar xk−xk−1 dan tinggi f(tk). Jika partisiP cukup halus, maka masuk akal untuk mengharapkan bahwa jumlah Riemann S(P, f) akan menghampiri luas daerah di bawah kurvay=f(x). Dalam hal ini, nilai S(P, f) mestilah cukup dekat ke nilai integral dari f pada I, bila f terintegralkan padaI.

pemilihan titik sampel tk∈Ik := [xk−1, xk], kita mempunyai mk ≤f(tk)≤Mk, k= 1,2, . . . , n, dengan mk:= inff(Ik) danMk:= supf(Ik). Akibatnya,

n

X

k=1

mk(xk−xk−1)≤ n

X

k=1

f(tk)(xk−xk−1)≤ n

X

k=1

Mk(xk−xk−1),

yakni

L(P, f)≤S(P, f)≤U(P, f).

Jadi, jumlah Riemann untukf senantiasa bernilai di antara jumlah Riemann bawah dan jumlah Riemann atas, terlepas dari bagaimana caranya kita memilih titik-titik sampeltk.

Catat khususnya jika batas bawahmk dan batas atasMk tercapai olehf pada [xk−1, xk] untuk tiapk= 1,2, . . . , n, maka jumlah Riemann bawah dan jumlah Rie-mann atas sama dengan jumlah RieRie-mann untuk titik-titik sampel tertentu. Secara umum, jumlah Riemann bawah maupun atas bukan jumlah Riemann (karena nilaimk dan Mk tidak harus tercapai oleh f). Namun demikian, dengan memilih titik-titik sampel secara cermat, kita dapat memperoleh jumlah Riemann yang cukup dekat ke jumlah Riemann bawah atau ke jumlah Riemann atas.

Soal Latihan

1. Misalkan f(x) =x, x∈[0, b]. Untuk sembarang partisi P :={x0, x1, . . . , xn} dari [0, b], pilih titik-titik sampeltk =1₂(xk+xk−1). Hitunglah jumlah Riemann S(P, f) dengan titik-titik sampel ini.

2. Misalkan f : I → R terbatas, P :={x0, x1, . . . , xn} partisi dari I, danǫ >0 sembarang.

(a) Tentukan titik-titik sampeltk sedemikian sehingga n

X

k=1

f(tk)(xk−xk−1)−L(P, f)< ǫ.

(b) Tentukan titik-titik sampeltk sedemikian sehingga U(P, f)−

n

X

k=1

15.2 Integral sebagai Limit

Di sini kita akan melihat bahwaRb

af(x)dxdapat dipandang sebagai ‘limit’ dari jumlah RiemannS(P, f), dalam arti tertentu.

Teorema 1. Misalkan f terintegralkan pada I. Maka, untuk setiap ǫ > 0 terdapat suatu partisi Pǫ dari I sedemikian sehingga untuk sembarang partisi P ⊇ Pǫ dan

sembarang jumlah RiemannS(P, f)berlaku

S(P, f)− Z b

a

f(x)dx < ǫ.

Bukti. Diberikanǫ >0 sembarang, pilih partisiPǫ dariI sedemikian sehingga U(Pǫ, f)−L(Pǫ, f)< ǫ.

Selanjutnya ambil sembarang partisiP ⊇Pǫ. Maka, menurut Proposisi 1 pada Sub-bab 13.1, kita mempunyai

L(Pǫ, f)≤L(P, f)≤U(P, f)≤U(Pǫ, f). Akibatnya,

U(P, f)−L(P, f)< ǫ.

Sekarang misalkan S(P, f) adalah sembarang jumlah Riemann yang terkait dengan P. Maka,

L(P, f)≤S(P, f)≤U(P, f). Sementara itu, kita juga mempunyai

L(P, f)≤

Z b

a

f(x)dx≤U(P, f). Dari kedua ketaksamaan ini kita peroleh

S(P, f)− Z b

a

f(x)dx

≤U(P, f)−L(P, f)< ǫ,

dan teorema pun terbukti.

Teorema 2. Misalkan f terbatas pada I. Misalkan terdapat suatu bilangan A ∈R

sedemikian sehingga untuk setiapǫ >0terdapat partisiPǫdariIsedemikian sehingga

untuk sembarang partisi P ⊇Pǫ dan sembarang jumlah RiemannS(P, f)berlaku |S(P, f)−A|< ǫ.

Makaf terintegralkan pada I dan

Z b

a

f(x)dx=A.

Soal Latihan

1. Buktikan Teorema 2.

2. Misalkan f(x) = x, x∈[0, b]. Gunakan Teorema 1 dan Soal Latihan 15.1 No. 1 untuk menyimpulkan bahwaRb

0x dx= 1 2b2.

3. Gunakan Teorema 1 untuk memberikan bukti alternatif untuk Teorema Dasar Kalkulus II (Teorema 6 pada Sub-bab 14.2).

15.3 Teorema Darboux

Terdapat cara lain melihat integral sebagai limit dari jumlah Riemann. Misal-kanI:= [a, b] danP:={x0, x1, . . . , xn}adalah partisi dariI. Ukurankehalusandari P, dilambangkan dengankPk, didefinisikan sebagai

kPk:= sup{xk−xk−1 : k= 1,2, . . . , n}.

Dalam perkataan lain, kPk adalah panjang sub-interval maksimum yang terkait de-ngan partisiP.

Catat bahwa dua partisi berbeda dapat memiliki kehalusan yang sama. Selain itu, jikaP ⊆Q(yakni, Qmerupakan perhalusan dariP), makakQk ≤ kPk. Namun sebaliknyakQk ≤ kPk tidak mengharuskanP ⊆Q.

Teorema 3 (Teorema Darboux). Misalkan f terintegralkan padaI. Maka, untuk setiap ǫ >0 terdapat δ >0 sedemikian sehingga jika Qadalah partisi dari I dengan

kQk< δ, maka untuk sembarang jumlah RiemannS(Q, f)berlaku

ǫdanQ∗mempunyai sebanyak-banyaknyan−1 titik lebih banyak daripada Q, yakni titik-titik x1, . . . , xn−1 yang ada di Pǫ tetapi sebanyak-banyaknya 2(n−1) suku berbentuk

(Mj−Mk∗)(zk−zk−1),

dengan Mj menyatakan supremum dari f pada sub-interval ke-j dalam Q dan Mk∗ menyatakan supremum darif pada sub-interval ke-kdalamQ∗_{. Karena|M}

j−Mk∗| ≤ Serupa dengan itu kita juga mempunyai

L(Q∗_{, f)−}ǫ

Selanjutnya kita tahu bahwa S(Q, f) dan Rb

a f(x)dx terletak dalam interval [L(Q, f), U(Q, f)], dan karena itu keduanya berada dalam interval

Iǫ:= [L(Q∗, f)− ǫ 3, U(Q

∗_{, f) +} ǫ 3]. Karena Q∗ _{⊇ Pǫ, kita mempunyai U(Q}∗_{, f)−L(Q}∗_{, f) <} ǫ

3, sehingga panjang Iǫ lebih kecil daripadaǫ. Jadi jarak antaraS(Q, f) dan Rb

af(x)dx mestilah lebih kecil daripadaǫ, sebagaimana yang ingin kita buktikan.

Kebalikan dari Teorema 3 juga berlaku.

Teorema 4. Misalkan f :I→R terbatas. Misalkan terdapat suatu bilangan B ∈R

sedemikian sehingga untuk setiap ǫ > 0 terdapat δ > 0 sedemikian sehingga untuk sembarang partisiP dari I dengankPk< δ dan sembarang jumlah RiemannS(P, f)

berlaku

|S(P, f)−B|< ǫ.

Makaf terintegralkan pada I dan

Z b

a

f(x)dx=B.

Soal Latihan

1. Buktikan Teorema 4. (Petunjuk. Gunakan Teorema 2.)

2. Buktikan bahwafterintegralkan jika dan hanya jika untuk setiapǫ >0 terdapat δ >0 sedemikian sehingga jikakPk< δ dankQk< δ, maka

16. BARISAN FUNGSI

16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik

Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan membahas keluarga fungsi yang membentuk suatu barisan. Dalam aplikasi, barisan fungsi muncul ketika kita berupaya menghampiri sebuah fungsi dengan keluarga fungsi yang kita kenal baik.

Sebuahbarisan fungsiadalah suatu pengaitann7→fn,n∈N, yang kita tuliskan sebagaihfni. Di sinifnmerupakan fungsi dan untuk tiapn∈Nkita asumsikan bahwa fn mempunyai daerah asal yang sama, sebutlahA⊆R.

Seperti pada pembahasan barisan bilangan real, ketika dihadapkan dengan se-buah barisan fungsi hfni kita akan tertarik untuk membahas perilaku fn apabila n→ ∞. Dalam perkataan lain, kita ingin mempelajari kekonvergenan barisanhfni padaA.

Mengingat bahwa untuk tiapx∈A, fn(x) membentuk suatu barisan bilangan real, maka kekonvergenan barisan fungsi hfnidapat didefinisikan melalui kekonver-genan barisan bilangan hfn(x)i. Bila untuk tiap x∈ A, barisanhfn(x)i konvergen ke suatu bilangan (yang secara umum bergantung pada x), sebutlah Lx, maka kita peroleh sebuah fungsi f :A → Rdengan f(x) = Lx. Jadi, untuk tiap x ∈A, kita mempunyai

fn(x)→f(x), n→ ∞.

Dalam hal ini, kita katakan bahwa hfni konvergen titik demi titik ke f, dan kita tuliskan

Contoh 1. Misalkan untuk tiapn∈Nkita mempunyai fn(x) :=xn, x∈[0,1].

Maka, barisan fungsihfnikonvergen titik demi titik ke fungsif dengan

f(x) :=

0, 0≤x <1; 1, x= 1.

Untuk mendapatkan gambaran tentang apa yang terjadi, gambarlah grafik beberapa buah fungsifn dan juga grafik fungsif, pada sebuah sistem koordinat yang sama.

Dalam Contoh 1 kita melihat bahwafn kontinu pada [0,1] untuk tiapn∈N, namunf tidak kontinu pada [0,1]. Jadi, kekonvergenan titik demi titik secara umum tidak mempertahankan sifat kekontinuan fungsi. Padahal, dalam aplikasinya, ini merupakan salah satu isu penting. Oleh karena itu, dalam pembahasan berikutnya, kita akan mempelajari jenis kekonvergenan barisan fungsi yang lebih kuat, yang mem-pertahankan antara lain sifat kekontinuan fungsi.

Diberikan suatu barisan fungsihfki, kita mempunyai deretfungsi ∞

P

k=1

fk,yang didefinisikan sebagai limit titik demi titik dari barisan jumlah parsialPn

k=1

fk, asalkan barisan jumlah parsial ini konvergen.

Jika barisan jumlah parsial tersebut konvergen titik demi titik ke fungsispada A, makasdisebut sebagaijumlahderet padaA. Dalam hal ini, kita tuliskan

∞

X

k=1

fk(x) =s(x), x∈A.

Secara umum, indekskdapat berjalan mulai dari sembarangk∈Z.

Sebagai contoh, jika fk(x) := xk, k = 0,1,2, . . ., maka kita peroleh deret geometri P∞

k=0

xk_{, yang konvergen ke} 1

1−x untuk|x|<1 (lihat kembali Bab 5). Pembahasan mengenai deret fungsi, khususnya deret yang berbentuk

∞

X

n=0

an(x−c)n

Soal Latihan

1. Tinjau barisan fungsi hfniyang dibahas dalam Contoh 1. Diberikan x∈[0,1] danǫ > 0, tentukanN ∈N sedemikian sehingga untuk setiapn ≥N berlaku |fn(x)−f(x)|< ǫ. (Catatan. Kasusx= 1 perlu ditangani tersendiri.)

2. Untuk masing-masing barisan fungsi di bawah ini, tentukan sebuah fungsi f yang merupakan limitnya (titik demi titik).

(a) fn(x) := xn

n , x∈[0,1].

(b) fn(x) :=nx(1−x2₎n_{, x∈[0,1].} (c) fn(x) := x

n, x∈R. (d) fn(x) := _1+xx2n2n, x∈R.

(e) fn(x) := sinnx

n√x, x >0.

16.2 Kekonvergenan Seragam

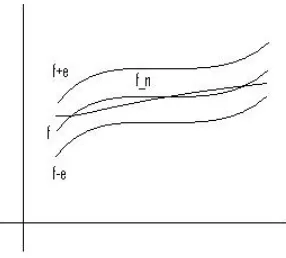
Misalkan hfni adalah suatu barisan fungsi yang, katakanlah, konvergen titik demi titik ke fungsi f padaA. Dalam hal ini, diberikan x∈ Adan ǫ >0, terdapat N ∈N sedemikian sehingga untuk setiapn≥N berlaku|fn(x)−f(x)|< ǫ. Secara umum bilangan N di sini bergantung pada x, selain pada ǫ. Bila bilangan N tadi berlaku untuk tiapx∈A, makahfnidikatakankonvergen seragamkef padaA.

Jadi, barisan fungsihfnikonvergen seragam kef padaAapabila untuk setiap ǫ >0 terdapatN ∈Nsedemikian sehingga untuk setiapn≥N danx∈Aberlaku

|fn(x)−f(x)|< ǫ. Dalam hal ini kita tuliskan

fn→f (seragam), n→ ∞.

Gambar 16.1_{Pita dengan lebar 2ǫdan median grafik fungsif}

Perhatikan bahwa ketaksamaan|fn(x)−f(x)|< ǫsetara dengan f(x)−ǫ < fn(x)< f(x) +ǫ.

Bila ini berlaku untuk setiapn≥N danx∈A, maka grafik fungsifn padaAberada di antara ‘pita’ [f −ǫ, f +ǫ] yang mempunyai lebar 2ǫ dan median grafik fungsi f, sebagaimana diilustrasikan dalam Gambar 16.1.

Contoh 2. Barisan fungsi hfni dengan fn(x) := xn, x ∈ [0,1], tidak konvergen seragam kef pada [0,1], dengan

f(x) :=

0, 0≤x <1; 1, x= 1.

Di sini, pita [f−1₄, f+1₄] tidak akan memuat grafikfn untuk nberapa pun. Lemma berikut (yang merupakan negasi dari definisi kekonvergenan seragam) dapat dipakai untuk menyelediki ketidakkonvergenan seragam suatu barisan fungsi.

Lemma 3. Barisan fungsi hfni tidak konvergen seragam ke fungsi f pada A jika

dan hanya jika untuk suatu ǫ0 >0 terdapat subbarisan hfnki dari hfni dan barisan

bilangan hxki diA sedemikian sehingga

Dengan menggunakan Lemma 3, ketidakkonvergenan seragam barisan fungsi

Ketidakkonvergenan seragam barisan dalam Contoh 2 juga dapat dijelaskan dengan teorema di bawah ini (yang mengatakan bahwa kekonvergenan seragam memperta-hankan sifat kekontinuan).

Teorema 4. Misalkanhfnikonvergen seragam kef pada suatu interval I⊆R. Jika fn kontinu di c∈I untuk tiapn∈N, maka f juga kontinu di c.

Bukti. Diberikan ǫ > 0, pilihN ∈ Nsedmeikian sehingga untuk setiap n≥N dan x∈I berlaku Ini membuktikan bahwaf kontinu dic.

Soal Latihan

2. Buktikan jikahfnidan hgnikonvergen seragam ke f dan g padaA (berturut-turut), makahfn+gnikonvergen seragam kef+g padaA.

3. Misalkanfn(x) :=x+1

n danf(x) =x, x∈R. Buktikan bahwahfnikonvergen seragam kef padaR, namunhfn2itidak konvergen seragam kef2 padaR.

16.3 Kriteria Cauchy untuk Kekonvergenan Seragam

Dalam membahas kekonvergenan seragam, seringkali kita terbantu dengan pe-ngertian norma seragam berikut. Ingat bahwa untuk A ⊆ R, fungsi f : A → R

dikatakan terbatas pada A apabila f(A) merupakan himpunan terbatas. Sekarang, jikaf terbatas padaA, maka kita definisikan norma seragamf padaAsebagai

kfkA:= sup{|f(x)| : x∈A}.

Perhatikan bahwakfkA< ǫsetara dengan|f(x)|< ǫuntuk tiapx∈A.

Menggunakan norma seragam, kita mempunyai lemma berikut tentang kekon-vergenan seragam.

Lemma 5. Misalkan fn terbatas pada A untuk tiap n ∈ N. Maka, barisan hfni

konvergen seragam kef pada Ajika dan hanya jika lim

n→∞kfn−fkA= 0.

Dengan menggunakan Lemma 5, kita juga dapat membuktikan ketidakkonver-genan seragam barisan fungsi dalam Contoh 2, dengan menghitung bahwa

kfn−fk[0,1]= 1 untuk tiapn∈N.

Dengan menggunakan norma seragam, kita peroleh pula kriteria berikut untuk kekonvergenan seragam suatu barisan fungsi.

Teorema 6 (Kriteria Cauchy untuk Kekonvergenan Seragam). Misalkan fn

terbatas pada A untuk tiap n∈ N. Maka, barisan hfni konvergen seragam ke suatu

fungsi terbatas f pada A jika dan hanya jika untuk setiap ǫ > 0 terdapat N ∈ N

Bukti. Misalkanhfnikonvergen seragam kef padaA. Diberikan ǫ >0 sembarang, pilih N ∈ N sedemikian sehingga untuk setiap n ≥ N berlaku kfn −fkA < 2ǫ. Akibatnya, jikam, n≥N, maka

|fm(x)−fn(x)| ≤ |fm(x)−f(x)|+|fn(x)−f(x)|< ǫ 2+

ǫ 2 =ǫ untuk tiapx∈A. Jadikfm−fnkA< ǫuntuk m, n≥N.

Sebaliknya, misalkan untuk setiapǫ >0 terdapatN ∈Nsedemikian sehingga untukm, n≥N kita mempunyaikfm−fnkA< ǫ. Maka, untuk setiapx∈A, berlaku

|fm(x)−fn(x)| ≤ kfm−fnkA< ǫ,

untuk m, n ≥ N. Ini berarti bahwa hfn(x)i merupakan barisan Cauchy di R, dan karenanya ia merupakan barisan yang konvergen, katakanlah ke f(x). Selanjutnya, untuk setiap x∈A, kita mempunyai

|fm(x)−f(x)|= lim

n→∞|fm(x)−fn(x)| ≤ǫ,

untukm≥N. Ini menunjukkan bahwahfnikonvergen seragam kef padaA.

Soal Latihan

1. Buktikan Lemma 5.

2. Misalkan hfni dan hgni adalah barisan fungsi terbatas pada A, yang konver-gen seragam ke f dan g pada A (berturut-turut). Tunjukkan bahwa hfngni konvergen seragam kef g padaA.

3. Uji-M Weierstrass. Misalkanhfniadalah barisan fungsi padaAdan|fn(x)| ≤ Mn untuk tiap x ∈ A dan n ∈ N. Buktikan jika P∞k=1Mk konvergen, maka deret fungsiP∞

17. PERTUKARAN LIMIT

17.1 Pertukaran Limit dan Turunan

Kita telah melihat sebelumnya bahwa kekonvergenan seragam mempertahankan sifat kekontinuan fungsi, yakni, jika fn kontinu pada A untuk tiap n ∈N dan hfni konvergen seragam kef padaA, makaf kontinu padaA.

Sekarang kita bertanya: apakah kekontinuan seragam juga mempertahankan sifat diferensiabilitas? Pertanyaan ini penting mengingat dalam aplikasi kita seringkali menaksir sebuah fungsi f dengan suatu deret P∞

n=1

fn (misalnya), dan kemudian kita menginginkan

f′_{(x) =} ∞

X

n=1 f′

n(x).

Jawaban untuk pertanyaan ini ternyata negatif. Sebagai contoh, fungsif yang didefi-nisikan sebagai jumlah deret berikut

f(x) := ∞

X

k=1

2−kcos(3kx)

merupakan fungsi yang kontinu di setiap titik tetapi tidak mempunyai turunan di titik manapun (lihat Bartle & Sherbert). Padahal, jumlah parsial deret ini mempunyai turunan di setiap titik dan membentuk barisan yang konvergen seragam kef. Jadi, kekonvergenan seragam dari suatu barisan fungsi yang mempunyai turunan ternyata tidak menjamin bahwa limitnya mempunyai turunan.

Teorema berikut memberikan suatu syarat cukup agar sebuah barisan fungsi mempertahankan sifat diferensiabilitas.

Teorema 1. Misalkan I⊆Radalah suatu interval terbatas dan hfni adalah barisan

barisanhf′

ni terdefinisi dan konvergen seragam ke suatu fungsig padaI. Maka,hfni

konvergen seragam ke suatu fungsif pada I denganf′_{(x) =g(x), x∈I.}

Bukti. Misalkan a < b adalah titik ujung interval I dan x ∈ I sembarang. Jika m, n ∈ N, maka menurut Teorema Nilai Rata-rata (untuk turunan) terdapat y di antarax0danxsedemikian sehingga

fm(x)−fn(x) =fm(x0)−fn(x0) + (x−x0)[f′

m(y)−fn(y)]. Akibatnya, kita peroleh

kfm−fnkI ≤ |fm(x0)−fn(x0)|+ (b−a)kfm′ −fn′kI.

Menurut hipotesis dan Kriteria Cauchy (Teorema 6, Bab 16),hfnikonvergen seragam padaI. Sebutlahf := lim

n→∞fn. Karenafn kontinu padaIuntuk tiapn∈N, makaf juga kontinu padaI.

Untuk menunjukkan bahwaf mempunyai turunan di sembarang titik c ∈ I, kita terapkan lagi Teorema Nilai Rata-rata terhadap fm−fn pada interval dengan titik ujungcdanx. Dalam hal ini terdapatzdi antarac danxsedemikian sehingga

[fm(x)−fn(x)]−[fm(c)−fn(c)] = (x−c)[f′

ni konvergen seragam pada I, untuk ǫ > 0 sembarang terdapat N ∈ N sedemikian sehingga jikam, n≥N danx6=c, maka

Jika kita ambil limit dari ruas kiri (terhadapm), maka kita dapatkan

M ∈ N sedemikian sehingga |f′

K := maks{M, N}. Karenaf′

K(c) ada, maka terdapatδK >0 sedemikian sehingga jika 0<|x−c|< δK, maka

Jadi, jika 0 < |x−c| < δK, maka (berdasarkan ketiga ketaksamaan di atas) kita mempunyai ke suatu fungsif yang mempunyai turunan pada [0,1], dan hf′

nikonvergen ke suatu fungsig pada [0,1], tetapif′_(1)6=g(1).

17.2 Fungsi Eksponensial

Dalam Kalkulus, kita mendefinisikan fungsi eksponensial E(x) := ex _sebagai invers dari fungsi logaritma L(x) := lnx:=Rx

1 1

tdt, x >0. Namun, daripada meng-ulang apa yang telah kita pelajari dalam Kalkulus, kita akan mempelajari suatu cara lain mendefinisikan fungsi eksponensial, yaitu dengan meninjau Masalah Nilai Awal

E′_{(x) =E(x), E(0) = 1. (3)} Perhatikan bahwa Masalah Nilai Awal ini setara dengan persamaan integral

E(x) = 1 +

Z x

0

E(t)dt.

Untuk mendapatkan solusinya, kita lakukan iterasi Picard dengan hampiran awal E0(x) := 1 dan

En+1(x) := 1 +

Z x

0

Dalam hal ini, kita akan memperoleh barisan fungsi

Sekarang marilah kita pelajari barisan fungsi ini. MisalkanR >0. Jika|x| ≤R danm > n >2R, maka

n! = 0, kita simpulkan bahwa barisan hEni konvergen seragam pada [−R, R] untuk R >0 sembarang.

Sebagai akibatnya, kita mempunyai teorema berikut.

Teorema 2. Barisan hEnikonvergen titik demi titik ke suatu fungsiE yang kontinu

padaR, denganE(0) = 1.

Bukti. Berdasarkan penjelasan di atas, jelas bahwa hEn(x)i konvergen untuk tiap x∈R. DefinisikanE:R→Rdengan

E(x) := lim

n→∞En(x), x∈R.

Karena setiapx∈Rtermuat dalam suatu interval [−R, R], makaE kontinu padaR. Selanjutnya, karenaEn(0) = 1 untuk tiapn, makaE(0) = 1.

Lebih jauh, kita mempunyai:

Teorema 3. E mempunyai turunan dengan E′_{(x) =E(x)untuk tiap x∈R.}

Bukti. Mengingat bahwaEn mempunyai turunan danEn+1′ (x) =En(x) untuk tiap n= 0,1,2, . . ., barisan hE′

pada sembarang interval [−R, R]. Dengan demikian, E′_{(x) = E(x) untuk tiap x∈}

R.

Akibat 4. FungsiE mempunyai turunan ke-k untuk tiapk∈N, dengan E(k)_{(x) =} E(x) untuk tiapx∈R.

Teorema 5. FungsiE yang memenuhi Masalah Nilai Awal (3) adalah tunggal. Teorema 6. FungsiE yang memenuhi Masalah Nilai Awal (3) bersifat:

(i)E(x)6= 0 untuk tiap x∈R;

17.3 Pertukaran Limit dan Integral

Sekarang mari kita periksa apakah kekonvergenan titik demi titik memperta-hankan keterintegralan. Misalkan fn(x) := nx(1−x2)n, x ∈ [0,1] (Soal 16.1 No.

Dengan demikian, untuk barisan fungsi ini, kita melihat bahwa

lim

Pertanyaannya sekarang adalah: bilakah limit dan integral dapat bertukar

tem-Teorema berikut menyatakan bahwa kekonvergenan seragam mempertahankan keter-integralan dan menjamin bahwa limit dan integral dapat betukar tempat.

Teorema 7. Misalkan fn terintegralkan pada I:= [a, b] untuk tiapn∈ Ndan hfni

Bukti. Diberikanǫ >0, pilihN∈Nsedemikian sehingga untuk setiapm≥N berlaku kf−fmkI <

ǫ 4(b−a).

Selanjutnya, karena fN terintegralkan, maka menurut Kriteria Riemann, terdapat partisiPǫ:={x0, x1, . . . , xn}dariI sedemikian sehingga Dengan cara yang serupa, kita juga peroleh

Selanjutnya, untuk membuktikan bahwa limit dan integral dapat bertukar

18. DERET PANGKAT

18.1 Deret Pangkat dan Interval Kekonvergenannya

Pada Bab 16 (dan, jauh sebelumnya, yaitu pada Bab 5) kita telah membahas deret geometri P∞

n=0

xn_{, yang konvergen (titik demi titik) ke} 1

1−x untuk|x|<1. Pada Bab 17, tepatnya pada Sub-bab 17.2, kita berurusan dengan deret P∞

n=0 xn

n!, yang kon-vergen (seragam) pada sembarang interval [−R, R],R >0. Kedua deret ini termasuk dalam keluargaderet pangkat

∞

X

n=0

an(x−c)n, (4)

yang akan kita pelajari secara lebih mendalam sekarang.

Deret pangkat (4) jelas konvergen untukx=c. Teorema berikut menunjukkan bahwa sebuah deret pangkat secara umum konvergen pada suatu interval yang ber-pusat dic.

Teorema 1. Jika deret P∞

n=0

an(x−c)n _{konvergen untuk x=x}

0, maka deret tersebut

juga konvergen (mutlak) untukxdengan|x−c|<|x0−c|.

Bukti. Karena P∞

n=0

an(x0 −c)n konvergen, maka an(x0 −c)n → 0 bila n → ∞. Akibatnya, barisanhan(x0−c)niterbatas, yakni terdapatM sedemikian sehingga

|an(x0−c)n| ≤M, n= 0,1,2, . . . . Sekarang misalkan|x−c|<|x0−c|. Maka

r= |x−c| |x0−c| <1. Akibatnya

Karena deret P∞

n=0

rn _{konvergen, maka menurut Uji Banding deret} P∞

n=0

an(x−c)n juga konvergen (mutlak).

Untuk selanjutnya, himpunan semua bilangan x ∈ R di mana deret pangkat ∞

P

n=0

an(x−c)n konvergen disebut interval kekonvergenan deret tersebut. Jika titik ujung interval kekonvergenan tersebut adalahc−Rdanc+R(denganR≥0), maka R disebut jari-jari kekonvergenan deret P∞

n=0

an(x−c)n_{. Interval kekonvergenannya} dalam hal ini adalah (c−R, c+R), (c−R, c+R], [c−R, c+R), atau [c−R, c+R]. Jika interval kekonvergenannya adalahR, maka jari-jari kekonvergenannya tak terhingga.

Contoh 2. (a) Interval kekonvergenan deret geometri P∞

n=0

xn _{adalah (−1,1), jari-jari} kekonvergenannya sama dengan 1.

(b) Interval kekonvergenan deret P∞

n=0 xn

n! adalahR. [Ingat bahwa deret ini konvergen pada sembarang interval [−R, R], R >0.]

Soal Latihan

1. Tentukan interval kekonvergenan deret pangkat berikut. (Petunjuk. Gunakan subsitusi peubah, misalt=x−1 untuk deret pertama.)

(a) P∞

Pada sub-bab terdahulu kita telah membuktikan bahwa sebuah deret pangkat ∞

P

n=0

Teorema 3. Misalkan lim

ada atau tak terhingga, katakanlah sama dengan

R. Maka, deret P∞

n=0

an(x−c)n _{konvergen bila|x−c|< Rdan divergen bila|x−c|> R.}

Bukti. Misalkan 0 < R < ∞. (KasusR = 0 atau tak terhingga diserahkan sebagai latihan.) Menggunakan Uji Rasio, deret P∞

n=0

Uji Rasio juga memberi tahu kita bahwa deret akan divergen bila|x−c|> R.

Catatan_{. Teorema di atas tidak memberi tahu kita perihal kekonvergenan deret untuk}

x=c±R. Namun, kita dapat memeriksa kedua kasus tersisa ini secara tersendiri, dengan menggunakan pengetahuan kita tentang deret bilangan.

Contoh 4. (a) Untuk deret geometri P∞

n=0

xn_{, kita mempunyai a}

n = 1 untuk tiap n∈N. Karena itu, jari-jari kekonvergenannya adalah

R= lim

Jadi deret konvergen bila |x| < 1 dan divergen bila|x| > 1. Untukx =±1, deret jelas divergen. Dengan demikian, interval kekonvergenan deret adalah (−1,1), seba-gaimana telah kita ketahui sebelumnya.

(b) Untuk deret P∞

Jadi deret konvergen untuk setiapx∈R. Apa yang terjadi bila barisanD an

an+1

E

Teorema 5. Misalkan L := lim sup n→∞

|an|1/n ada atau tak terhingga, dan R := 1 L.

Maka, deret P∞

n=0

an(x−c)n _{konvergen bila|x−c|< R dan divergen bila|x−c|> R.}

Soal Latihan

1. Buktikan Teorema 3 untuk kasusR= 0 danR=∞.

2. Tentukan jari-jari kekonvergenan deret berikut, dan kemudian tentukan interval kekonvergenannya.

(a) P∞

n=0 xn

n. (b) P∞

n=0 xn+1

2n .

(c) P∞

n=0 x2n

(2n)!

3. Buktikan Teorema 5.

18.3 Kekonvergenan Seragam Deret Pangkat

Teorema berikut menyatakan bahwa deret pangkat senantiasa konvergen ser-agam pada sembarang interval kompakdi dalaminterval kekonvergenannya.

Teorema 6. Jika R adalah jari-jari kekonvergenan deret pangkat P∞

n=0

anxn, maka

deret konvergen seragam pada sembarang interval kompakK⊆(−R, R).

Bukti. Hipotesis bahwa K kompak dan termuat dalam (−R, R) mengakibatkan adanya suatu konstanta c < 1 sedemikian sehingga |x| < cR untuk tiap x ∈ K. Karena itu,

|anxn| ≤ |an|cnRn =:Mn, n= 0,1,2, . . . . Menurut Uji Rasio, P∞

n=0

Mn konvergen. Akibatnya, berdasarkan Uji-M Weierstrass (Soal No. 3, Sub-bab 16.3), P∞

n=0

Akibat 7. Jumlah suatu deret pangkat merupakan fungsi yang kontinu pada(−R, R), denganR adalah jari-jari kekonvergenan deret pangkat tersebut.

Akibat 8. Sebuah deret pangkat dapat diintegralkan suku demi suku (yakni, inte-gral dan sigma dapat bertukar) pada sembarang interval kompak di dalam interval kekonvergenannya.

Akibat 9. Sebuah deret pangkat dapat diturunkan suku demi suku (yakni, turunan dan sigma dapat bertukar) di dalam interval kekonvergenannya. Persisnya, jikaf(x) =

∞

nanxn−1 juga mempunyai jari-jari

kekonvergenan R.

Perhatikan bahwa dalam Akibat 9 kita mempunyaia0 =f(0) dan a1 =f′(0). Jika fungsi f mempunyai turunan ke-ndi titikc untuk tiapn∈N, maka kita dapat menghitung koefisien Taylor an := f

(n)_(c)

n! untuk tiapn∈ Ndan memperoleh suatu deret pangkat dengan koefisien-koefisien ini. Namun, tidak ada jaminan bahwa deret pangkat yang dihasilkan konvergen kef pada suatu interval terbuka yang memuatc. Kekonvergenan deret pangkat tersebut bergantung pada suku sisaEndalam Teorema Taylor (Teorema 5, Sub-bab 10.3). Dalam hal ini, kita mempunyaideret Tayloruntuk f di sekitarc, yaitu

4. Buktikan bahwa deret pangkat P∞

n=0

5. Buktikan jika P∞

n=0

anxn dan ∞

P

n=0

bnxn konvergen ke suatu fungsi f yang sama pada suatu interval (−r, r) dengan r >0, makaan=bn untuk tiapn∈N. 6. Buktikan dengan induksi bahwa fungsifdenganf(x) =e−1/x2

DAFTAR PUSTAKA

1. R.G. Bartle and D. Sherbert, Introduction to Real Analysis, 3rd ed., John Wiley & Sons, 19xx.