6
BAB II
LANDASAN TEORI
Pada bab ini akan diuraikan konsep-konsep dasar yang digunakan sebagai landasan pembahasan pada bab selanjutnya yaitu sistem dinamik, nilai eigen, solusi sistem linear, linearisasi, kestabilan titik kesetimbangan, kriteria Routh Hurwitz, model matematika, pertumbuhan logistik, mekanisme Michaelis Menten, imunitas, virus, kemoterapi, dan immunoterapi.
A. Sistem Dinamik
Pada sistem dinamik, perubahan keadaan terjadi setiap saat. Perubahan-perubahan tersebut dapat diturunkan sebagai fungsi dari waktu. Dengan kata lain, sistem dinamik adalah sistem yang variabel-variabelnya berinteraksi untuk menstimulasi perubahan waktu. Sistem dinamik memberikan gambaran secara fungsional terhadap solusi masalah-masalah fisik atau model matematika yang menggambarkan masalah fisik.
Sesuai kajian matematika, sistem dinamik merupakan suatu himpunan variabel-variabel yang berhubungan dengan perubahan waktu.
Definisi 1 (Perko, 2001: 182)
Suatu sistem dinamik pada E adalah suatu pemetaan C1
: E E
dengan 1
C adalah himpunan fungsi-fungsi yang turunan pertamanya kontinu, n
7 i. 0( )x x, x E
ii. t( )x s( )x t s( ),x s t, dan x E
Keadaan setimbang dikenal dengan beberapa istilah, sesuai dengan wawasan yang dikaji. Pada bidang ekologi dan ekonomi istilah kesetimbangan (equilibrium) sangat umum dipakai untuk menggambarkan dinamika sistem yang tidak mengalami gejolak (Rudy C Tarumingkeng, 1994: 284). Apabila salah satu subsistem atau komponen suatu sistem yang berada dalam keadaan setimbang mengalami gangguan maka seluruh sistem akan berubah. Besarnya perubahan mungkin dalam kuantitas yang sangat kecil, tetapi setelah beberapa waktu gangguan ini dapat memberikan akibat yang mungkin tidak terduga sebelumnya.
Definisi 2 (Wiggins, 1990: 5)
Diberikan sistem persamaan diferensial berikut: ( ),
x f x x n (2.1) Titik kesetimbangan sistem (2.1) adalah suatu solusi x x yang memenuhi
( ) 0.
f x
Contoh:
Diberikan sebuah sistem dinamik sebagai berikut:
1 1 2 2 10 5 x x x x (2.2)
8 10 5 0 0 t t t e e , 0 0 1 0 2 x x x dan 0 0 10 1 5 2 0 . 0 t t x e x t x e
Titik kesetimbangan sistem (2.2) adalah x x1, 2 0, 0 .
B. Nilai Eigen
Nilai eigen digunakan untuk menentukan solusi sistem linear dari suatu sistem dinamik.
Definisi 3 (Boelkins dkk, 2009: 86)
Misalkan A adalah matriks n n, maka vektor taknol v dinamakan vektor eigen dari A jika dan hanya jika terdapat skalar sedemikian sehingga
Av v
Skalar dinamakan nilai eigen yang bersesuaian dengan vektor eigen v.
Solusi dari masalah nilai eigen/eigen vektor dapat dituliskan secara ekivalen sebagai
(A I v) 0
dengan I menyatakan matriks identitas. Sistem dikatakan mempunyai solusi non trivial jika dan hanya jika
det(A I) 0
Jika diberikan A adalah matriks n n, polynomial berorde n p( ) yang didefinisikan sebagai
( ) det( )
9
disebut polinom karakteristik dari A , dan persamaan p( ) 0 disebut persamaan
karakteristik dari A. Contoh:
Tentukan nilai eigen dari matriks A berikut ini.
3 1 0
0 2 0
2 0 2
A .
Penyelesaian:
Nilai eigen dapat ditentukan melalui persamaan det(A I) 0 :
3 1 0 det( ) 0 2 0 0 2 0 2 A I 3 2 2 0 2 3 2 0
Sehingga diperoleh nilai eigen dari matriks A adalah 1 3 dan 2 3 2.
C. Solusi Sistem Linear
Sistem yang dibahas pada skripsi ini berbentuk non linear. Untuk mendapatkan solusi masalah yang berbentuk sistem non linear tidaklah mudah. Muncullah konsep solusi sistem linear berikut ini.
Diberikan sistem linear:
10 dengan n
x , A adalah matriks berukuran n n dan
1 n dx dt dx x dt dx dt
Solusi sistem (2.3) dengan kondisi awal x(0) x0 adalah
0
( ) At
x t e x
(2.4) Bukti bahwa x t( ) e xAt 0 adalah solusi sistem (2.3) adalah sebagai berikut
Bentuk eAtadalah suatu fungsi matriks n n yang didefinisikan oleh deret Taylor (Perko, 2001: 1) sedemikian hingga
1 ! n n At n A t e I n (2.5)
Deret (2.5) didiferensialkan suku demi suku sehingga diperoleh 1 1( 1)! 1 ! n n n n At At n n d A t A t e A I Ae dt n n
Maka turunan pertama dari eAt adalah
At At
d
e Ae
dt
Ketika t 0 memenuhi kondisi
0 At
t
11 Kemudian mengidentifikasi At
e dengan matriks fundamental yang memenuhi masalah nilai awal yang sama sebagai eAt yaitu:
'
A , (0) I
Hasil dari interpretasi fungsi matriks eksponensial eAt, dapat dituliskan solusi sistem linear dari:
x Ax , x(0) x0 adalah dalam bentuk
0
( ) At
x t e x
Terdapat tiga kasus, antara lain:
1. Menurut (Perko, 2001: 7), jika A mempunyai nilai eigen real dan berbeda, bentuk At e menjadi At e P jt 1 diag e P Bukti:
Jika A mempunyai nilai eigen real dan berbeda, P AP1 diag j .
1 1 j P AP diag P AP D A PDP 1 maka 2 3 ( ) ( ) ( ) ... 2! 3! ! n At At At At e I At n 2 1 2 3 1 3 1 1 1 ... 2! 3! ! n n At PD P t PD P t PD P t e PP PDP t n
12 2 2 1 1 1 1 ... 2! ! n n PD t PD t PP PDtP P P n 2 2 1 ( ...) 2! D t P I Dt P jt 1 Pdiag e P
Sehingga persamaan (2.4) menjadi
x t P 1 0
jt
diag e P x (2.6)
2. Menurut (Perko, 2001: 33), jika A mempunyai nilai eigen real dan kembar, bentuk eAt menjadi At e P 1 1 1 ... ( 1)! j k k t N t diag e P I Nt k Bukti:
Jika A mempunyai nilai eigen real dan kembar yaitu A S N
dengan N adalah matriks berukuran n n. Matriks N berukuran n n dikatakan
nilpotent orde k jika 1 0 k N dan Nk 0 serta 1 j P SP diag . 1 j P SP diag 1 P A N P D P A1 P N P1 D P AP1 D P NP1 P P AP P1 1 P D P NP P1 1 1 A PD NP P 1 A PDP N maka
13 2 3 ( ) ( ) ( ) ... 2! 3! ! n At At At At e I At n 2 3 1 2 1 3 1 1 ... 2! 3! At PDP N t PDP N t e PP PDP N t 2 1 1 2 2 3 1 2 1 1 2 3 3 1 1 2 3 3 ... 2! 3! PD P PDP N N t PD P PD P N PDP N N t PP PDP N t 2 2 1 3 3 1 2 3 1 2 3 1 2 2 1 1 2 1 ... ... ... 2! 3! 2! 2! 2! PD t P PD t P PD Nt P PDN t P N t PP PDtP PDNt P Nt 2 2 3 3 2 3 3 2 2 1 2 1 1 1 2 ... ... ... 2! 3! 2! 2! 2! D t D t D t Dt N t P I Dt P PDt P N P P N P P N Nt 2 2 2 3 3 2 2 1 2 1 1 1 2 1 1 ... ... ... 2! 2! 2! 2! D t D t Dt N t P I Dt P PDt P N P P N P P N PP Nt PP 2 2 1 1 1 ... ... 2! ( 1)! k k D t N t P I Dt P I Nt k 2 2 1 1 2 2 1 1 2 2 1 2 2 0 0 2! 0 0 1 0 0 0 0 1 0 0 0 0 ... ... 2! ( 1)! 0 0 0 0 0 0 1 0 0 0 2! k k n n t t t t N t P P I Nt k t t 2 2 1 1 1 1 1 2 2 1 0 2! 0 ... ( 1)! 0 0 1 2! k k n n t t N t P P I Nt k t t 1 1 1 1 0 0 ... ( 1)! 0 0 n t k k t e N t P P I Nt k e P 1 1 1 ... ( 1)! j k k t N t diag e P I Nt k .
14 Sehingga persamaan (2.4) menjadi
( ) x t P 1 1 1 0 ... ( 1)! j k k t N t diag e P I Nt x k (2.7)
3. Menurut (Perko, 2001: 28), jika A mempunyai nilai eigen kompleks, bentuk eAt
menjadi
At
e P diag cos sin 1
sin cos j j j a t j j b t b t e P b t b t Bukti:
Jika A mempunyai nilai eigen kompleks dan 1 j j
j j a b P AP diag b a 1 P AP D 1 A PDP maka 2 3 ( ) ( ) ( ) ... 2! 3! ! n At At At At e I At n 2 1 2 3 1 3 1 1 ... 2! 3! At PD P t PD P t e PP PDP t 2 2 1 1 1 ... 2! PD t PP PDtP P 2 2 1 ( ...) 2! D t P I Dt P
15 2 1 1 2 1 1 1 1 1 1 2 2 1 0 2! 0 1 ... 1 0 0 1 2! n n n n n n n n a b t b a a t b t b t a t P a t b t a b b t a t t b a 1 P 2 2 2 2 3 1 1 2 1 1 1 1 1 1 2 2 2 2 3 1 1 2 1 1 1 1 1 1 2 2 2 2 3 2 2 2 2 2 3 2 1 2! 2! 1 2! 2! 1 2! 2! 1 2! 2! n n n n n n n n n n n n n n n n a b t a b t a t b t a b t a b t a b t b t a b t a t P a b t a b t a t b t a b t a b t a b t b t a b t a t 1 P Baris 1 kolom 1: 2 2 2 3 2 3 4 2 2 4 1 1 1 1 1 1 1 1 1 1 3 6 1 ... 2! 3! 4! a b t a a b t a a b b a t 2 2 2 2 2 3 2 2 4 4 4 1 1 1 1 1 1 1 1 1 ... ... ... 2! 2! 2! 2!2! 4! a t b t a b t a b t b t a t 2 2 2 2 4 4 1 1 1 1 1 ... 1 ... 2! 2! 4! a t b t b t a t 1 1 cos a t e b t Baris 1 kolom 2: 2 3 3 3 3 4 3 4 2 1 1 1 1 1 1 1 1 1 1 3 4 4 ... 3! 3! 4! 4! a b t b t a b t a b t b t a b t 2 3 3 3 3 4 3 4 2 1 1 1 1 1 1 1 1 1 1 ... 2! 3! 3! 3! a b t b t a b t a b t b t a b t
16 2 2 3 3 3 3 1 1 1 1 1 1 ... ... 2! 3! 3! a t a t b t a t b t 1 1 sin a t e b t Baris 2 kolom 1: 2 3 3 3 3 4 2 1 1 1 1 1 1 1 1 1 1 3 4 4 2 ... 2! 3! 4! a b b t a b a b t a b t b t 2 3 3 3 3 4 3 4 2 1 1 1 1 1 1 1 1 1 1 ... 2! 3! 3! 3! a b t b t a b t a b t b t a b t 2 2 3 3 3 3 1 1 1 1 1 1 ... ... 2! 3! 3! a t a t b t a t b t 1 1 sin a t e b t Baris 2 kolom 2: 2 2 2 3 2 3 4 2 2 4 1 1 1 1 1 1 1 1 1 1 3 6 1 ... 2! 3! 4! a b t a a b t a a b b a t 2 2 2 2 2 3 2 2 4 4 4 1 1 1 1 1 1 1 1 1 ... ... ... 2! 2! 2! 2!2! 4! a t b t a b t a b t b t a t 2 2 2 2 4 4 1 1 1 1 1 ... 1 ... 2! 2! 4! a t b t b t a t 1 1 cos a t e b t
Jadi bentuk eAt menjadi
1 1 1 1 1 1 1 1 1 cos sin sin cos cos sin sin cos n n n n a t a t a t a t At a t a t n n a t a t n n e b t e b t e b t e b t e P e b t e b t e b t e b t At
e P diag cos sin 1
sin cos j j j a t j j b t b t e P b t b t
17 Sehingga persamaan (2.4) menjadi
x t P diag 1 0 cos sin sin cos j j j a t j j b t b t e P x b t b t (2.8) D. Linearisasi
Perilaku sistem non linear dapat diselidiki melalui perilaku linearisasi jika nilai eigen pada bagian real dari matriks linearisasinya tidak ada yang bernilai nol. Oleh karena itu, linearisasi dilakukan dengan menganalisa perilaku sistem di sekitar titik kesetimbangan.
Diberikan sistem non linear:
1 1 1 2 2 2 1 2 1 2 , ,..., , ,..., , ,..., n n n n n x f x x x x f x x x x f x x x (2.9)
Apabila sistem (2.9) mempunyai titik kesetimbangan x x1, 2,...,xn maka
1 1, 2,..., n 2 1, 2,..., n n 1, 2,..., n 0
f x x x f x x x f x x x . Pendekatan linear
fungsi f x x1 1, 2,...,xn ,f2 x x1, 2,...,xn ,…, fn x x1, 2,...,xn diperoleh dengan
menggunakan ekspansi Taylor di sekitar titik kesetimbangan x x1, 2,...,xn yaitu,
1 2 1 1 1 1 2 1 1 2 1 2 1 1 1 2 2 1 2 2 2 2 1 2 2 1 2 1 2 1 1 1 2 2 1 2 1 2 , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., n n n n n f n n n n n f n n f f f x x x f x x x x x x x x x x x x x x x f f f x x x f x x x x x x x x x x x x x x x f x x x 1 2 1 2 1 1 1 2 2 1 2 , ,..., , ,..., , ,..., n n n n n n n n f f f f x x x x x x x x x x x x x x x (2.10)
18 Pendekatan linear untuk sistem (2.9) adalah
1 2 1 1 1 1 1 2 1 1 1 2 2 2 1 2 1 2 2 2 2 2 1 2 1 1 1 2 2 2 1 2 1 2 1 1 , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., n n n n n f n n n n n n f n n n f f f x x x x x x x x x x x x x x x x x x x f f f x x x x x x x x x x x x x x x x x x x f x x x , 2,..., 1 1 2 1, 2,..., 2 2 1, 2,..., n n n n n n n n f n f f x x x x x x x x x x x x x x x x (2.11) dengan 1
f ,…, fn disebut sebagai bagian non linear yang selanjutnya dapat diabaikan karena nilai
1
f ,…, fn mendekati nol. Persamaan (2.11) dapat dituliskan sebagai matriks
1 1 1 1 2 1 2 1 2 1 2 1 2 2 2 1 2 1 2 1 2 2 2 1 1 2 1 2 1 2 , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., n n n n n n n n n n n n n n f f f x x x x x x x x x x x x x f f f x x x x x x x x x x x x x x f f f x x x x x x x x 1 1 2 2 1, 2,..., n n n n x x x x x x x x x x (2.12)
Misalkan y1 x1 x , 1 y2 x2 x ,…, 2 yn xn x maka diperoleh: n
1 1 1 1 2 1 2 1 2 1 2 1 2 2 2 1 2 1 2 1 2 2 2 1 1 2 1 2 1 2 , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., n n n n n n n n n n n n n n f f f x x x x x x x x x x x x y f f f x x x x x x x x x y x x x y f f f x x x x x x x x 1 2 1, 2,..., n n n y y y x x x x (2.13)
19 dengan 1 1 1 1 2 1 2 1 2 1 2 2 2 2 1 2 1 2 1 2 2 1 1 2 1 2 1 2 1 2 , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., , ,..., n n n n n n n n n n n n n n n f f f x x x x x x x x x x x x f f f x x x x x x x x x x x x J f f f x x x x x x x x x x x x disebut
sebagai matriks Jacobian pada titik kesetimbangan x x1, 2,...,xn .
Apabila J tidak mempunyai nilai eigen yang bernilai nol pada bagian realnya maka sifat kestabilan sistem (2.9) dapat dilihat dari
y J y (2.14)
Sistem (2.14) kemudian disebut sebagai hasil linearisasi sistem (2.9).
E. Kestabilan Titik Kesetimbangan
Suatu titik kesetimbangan dapat dikatakan stabil, stabil asimtotik atau tidak stabil, diperlukan definisi dan teorema berikut ini.
Definisi 5 (Wiggins, 1990: 7)
Titik kesetimbangan x t dikatakan stabil jika diberikan 0 , terdapat
0 sedemikian hingga untuk solusi yang lain y t dari (2.1)
memenuhi x t0 y t0 dengan adalah norm pada n maka
x t y t untuk t t0, t0 .
Titik kesetimbangan x t dikatakan stabil asimtotik jika titik
20
bilangan konstan b 0 sedemikian hingga jika x t0 y t0 b maka
lim 0
t x t y t .
Titik kesetimbangan x 0 dikatakan tidak stabil jika titik kesetimbangan tersebut tidak stabil dan bergerak menjauhi titik kesetimbangannya seiring dengan bertambahnya t.
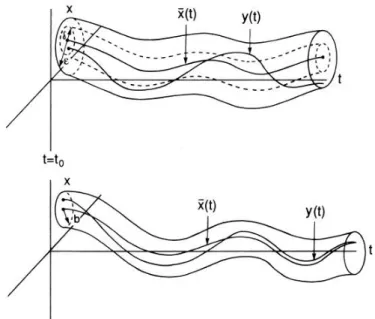
Berikut ini interpretasi secara geometri terkait definisi di atas:
Gambar 1. Titik Kesetimbangan Gambar 2. Titik Kesetimbangan
Stabil (atas) Stabil Asimtotik (bawah) Pada Gambar 1 menunjukkan bahwa solusi y t tetap berada pada persekitaran dan mendekati titik kesetimbangan seiring dengan bertambahnya t.
Pada Gambar 2 menunjukkan bahwa solusi y t bergerak menuju titik kesetimbangan seiring dengan bertambahnya t.
21
Teorema 1 (Olsder, 2004: 58)
Diberikan sistem x Ax, dengan A suatu matrik n n yang mempunyai k nilai eigen berbeda 1,..., k, dengan memenuhi k n .
Titik kesetimbangan x 0 dikatakan stabil jika Re i 0 untuk i 1,...,k.
Titik kesetimbangan x 0 dikatakan tidak stabil jika Re i 0 untuk beberapa 1,...,
i k dengan kata lain paling sedikit ada satu Re i 0. Bukti:
Perhatikan persamaan (2.6), (2.7), dan (2.8), ketiga persamaan ini merupakan solusi persamaan (2.5) untuk semua kemungkinan nilai eigen dari A. Setiap xi mempunyai
faktor e , dengan a tj
Re
j j
a , j 1, 2,...,n , sedangkan faktor lainnya bersifat terbatas sehingga:
(a) Jika Re j 0, j 1, 2,...,n maka saat t akan mengakibatkan nilai
Re
0
j t
e . Solusi dari sistem x x1, 2,...,xn 0, 0,..., 0 , artinya solusinya menuju ke titik kesetimbangannya maka sistem dapat dikatakan stabil.
(b) Jika ada j sehingga Re j 0 maka saat t nilai
Re j t
e , yang
mengakibatkan xj . Solusinya menjauh dari titik kesetimbangannya, maka sistem dapat dikatakan tidak stabil.
22
Nilai-nilai eigen dari suatu matriks A dapat ditentukan melalui persamaan karakteristiknya yaitu, A I 0. Dalam menentukan akar-akar persamaan karakteristik tidak selalu mudah. Oleh sebab itu, diperlukan kriteria yang menjamin bahwa akar-akar persamaan karakteristik adalah negatif atau terdapat akar persamaan yang bernilai positif.
Diberikan persamaan karakteristik nilai eigen dari suatu matriks A berukuran n n 1 0 1 ... 1 n n n n A I a a a a
dengan a0 0, sehingga dapat disusun tabel sebagai berikut.
Tabel 1. Tabel Routh Hurwitz
0 a a2 a4 1 a a3 a5 1 b b2 b3 1 c c2 c3 dengan 1 2 0 3 1 1 1 3 1 2 1 1 , , a a a a b a b a a b c b 1 4 0 5 2 1 1 5 1 3 2 1 , , a a a a b a b a a b c b
23
Bagian real nilai-nilai eigen dari matriks A yang berukuran n n akan bernilai negatif jika dan hanya jika tabel Routh Hurwitz mengandung n 1 baris dan semua elemen pada kolom pertama dari tabel bertanda sama yaitu semua elemen pada kolom pertama bernilai positif atau negatif secara keseluruhan.
G. Model Matematika
Model dapat dikatakan sebagai kata benda yang merupakan gambaran miniatur dari sesuatu, uraian atau analogi yang digunakan untuk membantu memvisualisasi segala sesuatu yang tidak dapat diamati secara langsung.
Pemodelan matematika adalah suatu studi tentang konsep matematika dalam konteks dunia real dan pembentukan model-model dalam menggali dan memahami situasi masalah kompleks yang sesungguhnya. Fokus pada pemodelan matematika adalah mentransformasikan situasi dunia real ke dalam masalah matematika melalui penggunaan rangkaian simbol matematika, hubungan dan fungsi.
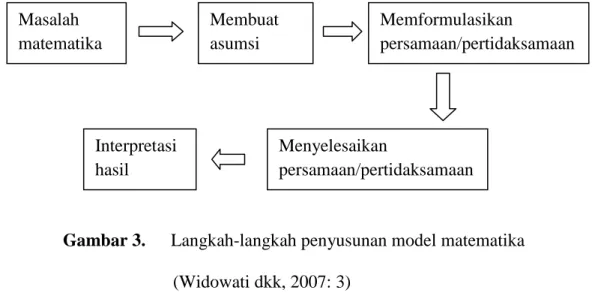
Bagian ini memaparkan proses penyusunan fenomena dalam dunia nyata ke dalam bentuk model matematika. Langkah-langkah dalam menyusun model matematika dalam skripsi ini diilustrasikan dalam alur diagram berikut:
24
Gambar 3. Langkah-langkah penyusunan model matematika
(Widowati dkk, 2007: 3) Keterangan:
a. Masalah matematika yaitu menyatakan masalah dunia nyata ke dalam pengertian matematika. Langkah ini meliputi identifikasi variabel-variabel dan membentuk beberapa hubungan antar variabel tersebut. Di samping itu, perlu memahami dan memperjelas permasalahan yang akan dirumuskan terutama mencari semua peubah yang kuantitatif dan antar relasinya sehingga dapat diterjemahkan ke dalam bahasa matematika.
b. Membuat asumsi
Asumsi ini mengibaratkan bagaimana proses berpikirnya agar model harus berjalan. Sama halnya, membuat asumsi agar mengarah pada situasi fisik yang kompleks menjadi masalah yang dapat diselesaikan.
c. Memformulasikan persamaan/pertidaksamaan
Melihat asumsi dan pemahaman hubungan antara variabel-variabel, memformulasikan sekumpulan persamaan/pertidaksamaan merupakan langkah
Masalah matematika Membuat asumsi Memformulasikan persamaan/pertidaksamaan Interpretasi hasil Menyelesaikan persamaan/pertidaksamaan
25
penting. Bahkan terkadang perlu menguji kembali asumsi-asumsi agar langkah memformulasi persamaan ini dapat diselesaikan dan realistik.
d. Menyelesaikan persamaan/pertidaksamaan
Setelah persamaan diperoleh, selanjutnya diselesaikan secara matematis dengan menggunakan sistem persamaan diferensial. Menyelesaikan persamaan diperlukan kehati-hatian dan fleksibilitas dalam proses pemodelan secara menyeluruh.
e. Interpretasi hasil
Interpretasi adalah langkah yang akan menghubungkan terakhir antara masalah matematika ke masalah dunia nyata. Hal ini dapat dilakukan dengan berbagai cara seperti suatu grafik dapat digambarkan berdasarkan solusi yang diperoleh.
H. Pertumbuhan Logistik
Sel tumor dan sel normal diasumsikan tumbuh mengikuti pertumbuhan logistik. Pertumbuhan logistik adalah model yang menggambarkan pertumbuhan populasi yang berkaitan dengan kapasitas lingkungan (carrying capacity) sebagai bentuk pengaruh dari persaingan. Menurut Arief Wahyullah, suatu populasi awalnya meningkat secara eksponensial kemudian akhirnya menurun hingga mendekati kapasitas lingkungannya karena sumber daya yang terbatas. Pertumbuhan populasi yang seperti ini dideskripsikan sebagai berikut:
26 1 dP P rP dt K (2.15)
dengan P t( ): jumlah populasi saat t, r 0: laju pertumbuhan, K 0: kapasitas lingkungan (carrying capacity).
I. Mekanisme Michaelis Menten
Kerja sistem imun pada model diasumsikan mengikuti bentuk Michaelis Menten. Bentuk ini biasanya digunakan pada model matematika terkait tumor yang mengandung komponen sistem imun karena memperbolehkan adanya pengaruh saturasi (kondisi jenuh).
Mekanisme Michaelis Menten adalah mekanisme tentang kinetika enzim. Menurut mekanisme ini, enzim mengikat substrat membentuk kompleks substrat-enzim. Kemudian terurai menjadi produk dan substrat-enzim.
1 2
1
k k
k
E S ES P E
Reaksi enzim tersebut dapat dimodelkan dalam sistem persamaan diferensial berikut:
2 1 ds k c k se dt 2 3 1 ( ) de k k c k se dt 1 ( 2 3) dc k se k k c dt (2.16) 3 dp k c dt
27 dengan
( ) [ ]( )
e t E t konsentrasi enzim pada saat t
( ) [ ]( )
s t S t konsentrasi substrat pada saat t
( ) [ ]( )
c t ES t konsentrasi kompleks substrat-enzim pada saat t
( ) [ ]( )
p t P t konsentrasi produk pada saat t
Selanjutnya misalkan et menyatakan enzim total yaitu jumlah enzim bebas E dan enzim terikat ES maka
t
e e c
t
e e c
ketika sistem reaksi berada dalam keadaan seimbang maka kecepatan pembentukan ES sama dengan kecepatan penguraian ES .
1 ( 2 3) k se k k c 1( t ) ( 2 3) k e c s k k c 1 t 1 ( 2 3) k e s k cs k k c 1 t ( 1 2 3) k e s k s k k c 1 1 2 3 ( ) t k e s c k s k k (2.17) Substitusi persamaan (2.13) ke dp k c3 dt diperoleh 2 3 1 ( ) / t e s c s k k k
28
(2.18)
bila konsentrasi substrat cukup besar sehingga semua enzim terikat kepadanya yaitu
dalam bentuk kompleks ES, maka akan didapatkan dp
dt maksimum yaitu maks k e3 t
sehingga k e3 t merupakan laju maksimum reaksi enzim yang dinotasikan
3
maks k et (2.19)
dengan memisalkan km (k2 k3) /k1 dan mensubstitusikan persamaan (2.15) dalam persamaan (2.18) diperoleh:
maxs
dp
dt km s (2.20)
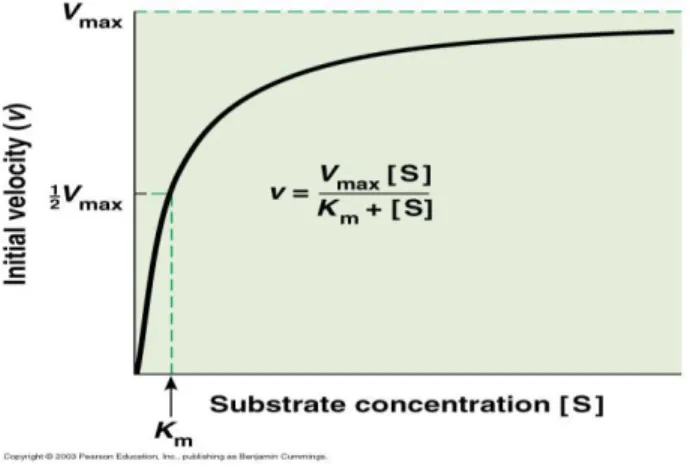
Grafik hubungan antara laju reaksi enzim dan konsentrasi substrat Michaelis Menten dapat dilihat pada gambar berikut.
Gambar 4. Hubungan antara laju reaksi enzim dan konsentrasi substrat 3 2 3 1 ( ) / t k e s dp dt s k k k
29
Persamaan Michaelis Menten di atas seringkali digunakan untuk menggambarkan laju pertumbuhan populasi yang bergantung pada konsentrasi nutrisi dan dapat mencapai kondisi jenuh saat konsentrasi nutrisi cukup besar atau melimpah. Misalkan konsentrasi dari nutrisi adalah s, maka laju pertumbuhan r(s) dinyatakan secara matematis berikut:
max
( ) s , 0
r s s
km s (2.21)
dengan max dan km adalah konstanta positif.
Persamaan (2.21) dikenal sebagai fungsi pertumbuhan monod. Grafik dari r s( ) akan mendekati nilai jenuh max yang merupakan laju pertumbuhan maksimal. Ketika
s km maka ( ) 2 maks
r s , karena itu km disebut sebagai konstanta half saturasi.
Konstanta ini juga disebut sebagai tetapan Michaelis Menten (Claudia, 2004: 771-774).
J. Imunitas
Sistem imun merupakan fundamental untuk mengetahui perkembangan sel tumor dalam memilih pendekatan terapi yang tepat.
Imunitas adalah sistem pertahanan tubuh sebagai bentuk perlindungan terhadap benda asing. Imunitas merupakan suatu daya ketahanan yang dinamis. Ketika terdapat hal-hal yang berbahaya bagi tubuh, maka timbul upaya untuk melawan. Reaksi tubuh yang demikian disebut reaksi atau respon imunologik.
30 Komponen respon imun:
1. Antigen, yaitu zat yang dapat bereaksi dengan antibodi.
2. Antibodi, yaitu protein yang diproduksi sebagai hasil interaksi dengan antigen. Terdapat 5 kelas antibodi yang disebut imunoglobin (A, D, E, G, M).
3. Imunoglobin G
Menyusun pertahanan untuk melawan bakteri dan virus dalam aliran darah. Ini merupakan satu-satunya antibodi yang mampu melintasi plasenta.
4. Imunoglobin M
Menghambat gerakan mikroorganisme patogen, memudahkan fagositosis dan dapat mengikat komplemen dengan kuat.
5. Imunoglobin A
Melindungi membran mukosa dari serangan bakteri dan virus. 6. Imunoglobin E
Bertindak sebagai reseptor untuk antigen. 7. Imunoglobin D
Bertindak sebagai reseptor antigen ketika terdapat sel B dan menandai kematangan sel B.
1. Komponen Sistem Imun
a. Fagosit
Fagosit adalah sel darah putih yang melindungi dengan menelan benda asing berbahaya, bakteri dan sel-sel mati. Proses menelannya ini dinamakan fagositosis.
31 b. Makrofag
Makrofag adalah sel penghasil fagosit yang berfungsi untuk menelan musuh seperti benda asing berbahaya, bakteri dan sel-sel mati sehingga tidak lagi menjadi suatu ancaman bagi tubuh.
c. Sel B
Sel B adalah sel-sel yang hanya mampu memproduksi antibodi sehingga berfungsi sebagai mediator imunitas humoral.
d. Sel T Penolong
Sebagai tanggapan terhadap rangsangan antigen, sel T penolong mensekresikan protein yang disebut sitokin, yang berfungsi untuk merangsang proliferasi dan diferensiasi sel T itu sendiri, serta sel lainnya, termasuk sel B, makrofag, dan leukosit lainnya dan membunuh sel-sel yang menghasilkan antigen asing, seperti sel yang terinfeksi oleh virus dan mikroba intraseluler lainnya.
e. Sel T Pembunuh
Terlibat dalam kekebalan bawaan terhadap virus dan mikroba intraseluler lainnya.
2. Respon imun terhadap virus
Sebenarnya di dalam tubuh terdapat sistem imun yang dapat menyerang virus yang masuk. Jika ada virus yang masuk, tubuh akan segera menyerangnya dengan cara sebagai berikut:
32
b. Tubuh menghasilkan antibodi dan antigen. Jika antigen masuk ke dalam tubuh, maka tubuh terpicu memproduksi antibodi. Antibodi ini sangat spesifik dan hanya menyerang pada antigen yang memicunya (Koes Irianto: 2006, 207).
K. Virus
Dalam skripsi ini, faktor yang dimaksudkan menyerang imun adalah virus. Virus adalah mikroorganisme berukuran sangat kecil yang mampu menginfeksi hampir semua jenis organisme. Virus juga dapat dikatakan sebagai makhluk peralihan antara hidup dan tak hidup. Hal ini disebabkan virus tidak mengalami pertumbuhan, tidak melakukan metabolisme dan tidak dapat berkembang biak dengan sendirinya.
L. Kemoterapi
Pendekatan terapi yang digunakan untuk membasmi sel tumor, yaitu kemoterapi. Kemoterapi adalah pengobatan dengan menggunakan zat-zat kimia yang bertujuan menghambat pertumbuhan sel tumor. Prinsip kerja obat kemoterapi adalah menyerang fase tertentu atau seluruh fase pada pembelahan mitosis pada sel-sel yang bereplikasi atau berkembang dengan cepat. Obat kemoterapi hampir tidak menimbulkan dampak pada sel yang sedang dalam masa beristirahat (tidak melakukan pembelahan), namun terkadang sel-sel rambut dan sel-sel yang sedang aktif membelah lainnya dapat terkena dampak obat ini apabila siklus mitosisnya
33
berada dalam target obat-obatan kemoterapi yang sedang digunakan. Menurut (Kianti Raisa Darusman, 2002: 6), sel tumor dapat berada dalam 3 keadaan yaitu:
1. Sel sedang melakukan pembelahan (siklus proliferatif).
2. Sel dalam keadaan istirahat (tidak melakukan pembelahan, G0).
3. Sel secara permanen tidak melakukan pembelahan.
Sel tumor yang sedang melakukan pembelahan terdapat dalam beberapa fase yaitu: a. fase mitosis (M)
b. fase pramitosis (G1)
c. fase sintesis DNA (S) d. fase pascamitosis (G2)
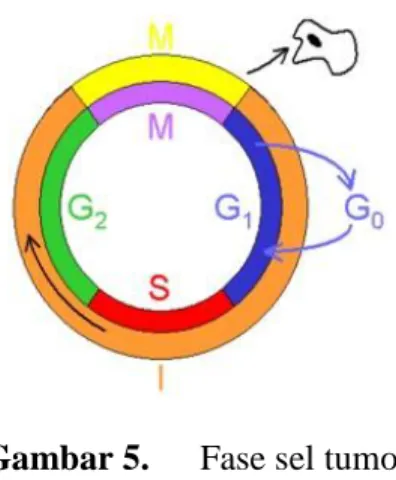
Bagan fase sel tumor adalah sebagai berikut:
Gambar 5. Fase sel tumor
Pada akhir fase G1 terjadi peningkatan RNA disusul dengan fase S yang
merupakan saat terjadinya replikasi DNA. Setelah fase S berakhir sel masuk dalam fase pramitosis (G2) dengan ciri-ciri :
34
b. mengandung DNA lebih banyak daripada sel fase lain c. masih berlangsungnya sintesis RNA dan protein
Sewaktu mitosis berlangsung (fase M) sintesis protein dan RNA berkurang secara tiba-tiba, dan terjadi pembelahan menjadi 2 sel. Setelah itu sel dapat memasuki interfase untuk kembali memasuki fase G1, saat sel berproliferasi atau memasuki fase
istirahat (G0). Sel dalam fase G0 yang masih potensial untuk berproliferasi disebut sel
induk (stem cell). Dengan demikian, sel dalam siklus proliferasi dan dalam fase G0
yang menambah jumlah sel tumor.
M. Immunoterapi
Adanya sel tumor dan virus dapat menyebabkan sistem imun makin melemah, pendekatan terapi yang efektif untuk mengatasi hal itu adalah immunoterapi. Immunoterapi adalah pengobatan yang berfungsi untuk merangsang sistem imun untuk melawan tumor. Immunoterapi mengacu pada penggunaan sitokin yang biasanya bersama-sama dengan adoptive cellular immunotherapy (ACI). Sitokin adalah protein hormon yang diproduksi oleh sel sebagai respon terhadap rangsangan berfungsi meningkatkan respon imun dengan cara merekrut dan mengaktivasi sel serta mengatur aktivasi dan diferensiasi sel T dan B. Sitokin yang paling efektif untuk penanganan hal tersebut adalah Interleukin-2 (IL-2), karena yang bertanggung jawab dalam pertumbuhan dan diferensiasi sel T.