BAB 2 DASAR TEORI 2.1 Umum (1,2,3,4)
Suatu sistem tenaga listrik (Electric Power System) terdiri dari tiga komponen utama, yaitu : sistem pembangkitan tenaga listrik, sistem transmisi tenaga listrik, dan sistem distribusi tenaga listrik .
Komponen dasar yang membentuk suatu sistem tenaga listrik adalah generator, transformator, saluran transmisi dan beban. Untuk keperluan analisis sistem tenaga, diperlukan suatu diagram yang dapat mewakili setiap komponen sistem tenaga listrik tersebut. Diagram yang sering digunakan adalah diagram satu garis dan diagram impedansi atau diagram reaktansi. Gambar 2.1 merupakan diagram satu garis sistem tenaga listrik yang sederhana.
G Pembangkit Transformator Step-up Transformator Step-down Penghantar Sistem Distribusi
Gambar 2.1 Diagram Satu Garis Sistem Tenaga Listrik
2.2 Aliran Daya (1,2,3,4)
Aliran Daya merupakan salah satu analisa sistem tenaga listrik pada keadaan
steady state. Besaran yang dihasilkan dari perhitungan studi aliran daya adalah daya
nyata (real power), daya reaktif (reactive power), besaran (magnitude), dan sudut beban (phase angle) tegangan pada setiap rel.
Jenis rel pada sistem tenaga, yaitu : 1. Rel Beban
dan reaktif yang dicatu ke dalam sistem tenaga adalah mempunyai nilai positif, sementara daya aktif dan reaktif yang di konsumsi bernilai negatif. Besaran yang dapat dihitung pada rel ini adalah V dan δ (sudut beban).
2. Rel Generator
Rel Generator dapat disebut dengan voltage controlled bus karena tegangan pada rel ini
dibuat selalu konstan atau rel dimana terdapat generator. Pembangkitan daya aktif dapat dikendalikan dengan mengatur penggerak mula (prime mover) dan nilai tegangan dikendalikan dengan mengatur eksitasi generator. Sehingga rel ini sering juga disebut dengan PV rel. Besaran yang dapat dihitung dari rel ini adalah Q dan δ (sudut beban).
3. Slack Bus
Slack Bus sering juga disebut dengan swing bus atau rel berayun. Adapun besaran yang
diketahui dari rel ini adalah tegangan (V) dan sudut beban (δ). Suatu sistem tenaga biasanya didesign memiliki rel ini yang dijadikan sebagai referensi yaitu besaran δ = 00. Besaran yang dapat dihitung dari rel ini adalah daya aktif dan reaktif.
Secara singkat klasifikasi rel pada sistem tenaga terdapat pada Tabel 2.1 yaitu besaran yang dapat diketahui dan tidak diketahui pada rel tersebut.
Tabel 2.1 Klasifikasi Rel Pada Sistem Tenaga Jenis rel Besaran yang
diketahui
Besaran yang tidak diketahui Rel beban (atau rel PQ) P, Q V , δ Rel generator atau rel
dikontrol tegangan (atau rel PV)
P, V Q , δ
Rel pedoman atau rel slack atau rel swing
2.2.1 Persamaan Aliran Daya (1)
Persamaan aliran daya secara sederhana, untuk sistem yang memiliki 2 rel. Pada setiap rel memiliki sebuah generator dan beban, walaupun pada kenyatannya tidak semua rel memiliki generator. Penghantar menghubungkan antara rel 1 dengan rel 2. Pada setiap rel memiliki 6 besaran elektris yang terdiri dari : PD, PG, QD, QG, V, dan δ.
G1 Rel 1 1 1∠δ V Beban 1 1 1 1 G G G P jQ S = + 1 1 1 D D D P jQ S = + Rel 2 2 2∠δ V Beban 2 2 2 2 G G G P jQ S = + 2 2 2 D D D P jQ S = + G2 Penghantar
Gambar 2.2 Diagram Satu Garis sistem 2 rel
Pada Gambar 2.2 dapat dihasilkan persamaan aliran daya dengan menggunakan diagram impedansi. Pada Gambar 2.3 merupakan diagram impedansi dimana generator sinkron direpresentasikan sebagai sumber yang memiliki reaktansi dan transmisi model π (phi). Beban diasumsikan memiliki impedansi konstan dan daya konstan pada diagram impedansi. G1 G2 B e b a 1 B e b a 2 1 ˆ E 1 G jX 1 ˆ G I 1 ˆ D I 1 ˆI ZS p y jB 2 yp jB 2 S R jXS 2 ˆ E 2 G jX 2 ˆ G I 2 ˆ D I 2 ˆI 1 ˆ V Vˆ2 n n
Gambar 2.3 Diagram impedansi sistem 2 rel
(
1 1) (
1 1)
1 1 1 SG SD PG PD j QG QD S = − = − + − (2.1)(
2 2) (
2 2)
2 2 2 SG SD PG PD j QG QD S = − = − + − (2.2)Pada Gambar 2.4 merupakan penyederhanaan dari Gambar 2.3 menjadi daya rel (rel daya) untuk masing-masing rel.
ˆ
Gambar 2.4 rel daya dengan transmisi model π untuk sistem 2 rel
Besarnya arus yang diinjeksikan pada rel 1 dan rel 2 adalah :
1 1 1 ˆ ˆ ˆ D G I I I = − (2.3) 2 2 2 ˆ ˆ ˆ D G I I I = − (2.4)
Semua besaran adalah diasumsikan dalam sistem per-unit, sehingga :
(
)
1 * 1 1 1 1 1 * 1 1 1 VˆIˆ P jQ P jQ Vˆ Iˆ S = = + ⇒ − = (2.5)(
)
2 * 2 2 2 2 2 * 2 2 2 VˆIˆ P jQ P jQ Vˆ Iˆ S = = + ⇒ − = (2.6) 1 ˆ I S S Z y = 1 p y 2 ˆ I 1 ˆ V 2 ˆ V p y S jX S R " ˆ 1 I ' ˆ 1 I " ˆ 2 I ' ˆ 2 I Rel Daya Rel DayaGambar 2.5 Aliran arus pada rangkaian ekivalen
1 1 1 ˆ ˆ ˆ I I I = ′+ ′′
(
)
S p V V y y V Iˆ1 = ˆ1 + ˆ1 − ˆ2(
)
1(
)
2 1 ˆ ˆ ˆ y y V y V I = p + S + − S (2.7) 2 12 1 11 1 ˆ ˆ ˆ Y V Y V I = + (2.8) Dimana :Y11 adalah jumlah admitansi terhubung pada rel 1 = yP +yS (2.9) Y12 adalah admitansi negatif antara rel 1 dengan rel 2 = −yS (2.10) Untuk aliran arus pada rel 2 adalah :
2 2 2 ˆ ˆ ˆ I I I = ′ + ′′
(
)
S p V V y y V Iˆ2 = ˆ2 + ˆ2 − ˆ1(
)
1(
)
2 2 ˆ ˆ ˆ y V y y V I = − S + p + S (2.11) 2 22 1 21 1 ˆ ˆ ˆ Y V Y V I = + (2.12) Dimana :Y22 adalah jumlah admitansi terhubung pada rel 2 = yP +yS (2.13) Y21 adalah admitansi negatif antara rel 2 dengan rel 1 = −yS =Y12 (2.14)
Dari Persamaan (2.8) dan (2.12) dapat dihasilkan Persamaan dalam bentuk matrik, yaitu : = 2 1 22 21 12 11 2 1 ˆ ˆ V V Y Y Y Y I I (2.15)
Notasi matrik dari Persamaan (2.15) adalah ::
bus bus bus Y V
Persamaan (2.5) hingga (2.16) yang diberikan untuk sistem 2 rel dapat dijadikan sebagai dasar untuk penyelesaian Persamaan aliran daya sistem n-rel.
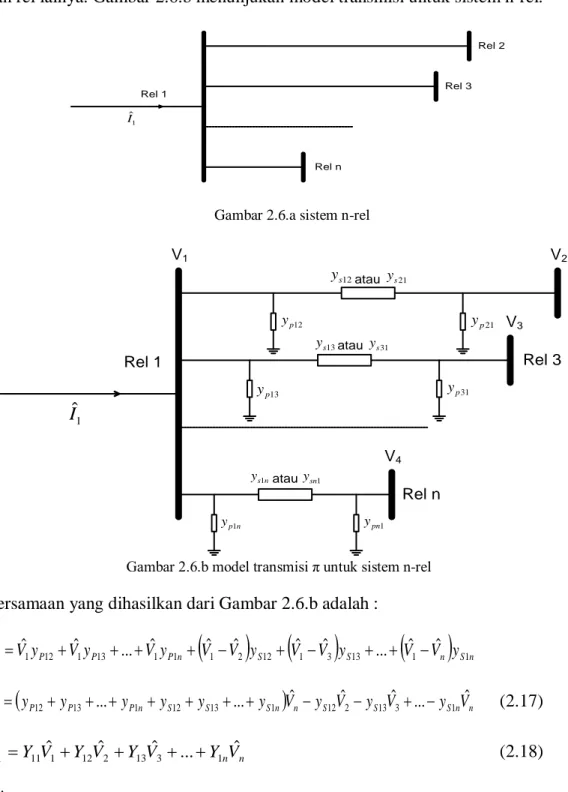
Gambar 2.6.a menunjukan sistem dengan jumlah n-rel dimana rel 1 terhubung dengan rel lainya. Gambar 2.6.b menunjukan model transmisi untuk sistem n-rel.
Rel 1 1 ˆ I Rel 2 Rel 3 Rel n
Gambar 2.6.a sistem n-rel
Rel 1 1 ˆ I Rel 2 12 p y yp21 12 s y atau ys21 Rel 3 13 p y yp31 13 s y atau ys31 Rel n 1 pn y n p y1 n s y1 atauysn1 V1 V2 V3 V4
Gambar 2.6.b model transmisi π untuk sistem n-rel
Persamaan yang dihasilkan dari Gambar 2.6.b adalah :
(
) (
S)
S(
n)
S n n P P P V y V y V V y V V y V V y y V Iˆ1 = ˆ1 12+ ˆ1 13+...+ ˆ1 1 + ˆ1− ˆ2 12+ ˆ1− ˆ3 13+...+ ˆ1− ˆ 1(
yP yP yPn yS yS ySn)
Vn yS V yS V ySnVn Iˆ1= 12+ 13+...+ 1 + 12+ 13+...+ 1 ˆ − 12ˆ2− 13ˆ3+...− 1 ˆ (2.17) n nV Y V Y V Y V Y Iˆ1 = 11ˆ1+ 12ˆ2 + 13ˆ3 +...+ 1 ˆ (2.18) Dimana : n S S S n P P P y y y y y y Y11= 12 + 13 +...+ 1 + 12 + 13 +...+ 1 (2.19)= jumlah semua admitansi yang dihubungkan dengan rel 1 n S n S S Y y Y y y Y12 =− 12; 13 =− 13; 1 =− 1 (2.20)
Persamaan (2.21) dapat disubtitusikan ke Persamaan (2.5) menjadi Persamaan (2.22), yaitu :
∑
= = n j j ijV Y I 1 1 ˆ ˆ (2.21)∑
= = = − n j j jV Y V I V jQ P 1 1 * 1 1 * 1 1 1 ˆ ˆ ˆ (2.22)∑
= = − n j j ij i i i jQ V Y V P 1 * ˆ ˆ i=1,2,...,n (2.23)Persamaan (2.23) merupakan representasi persamaan aliran daya yang nonlinear. Untuk sistem n-rel, seperti Persamaan (2.15) dapat dihasilkan Persamaan (2.24), yaitu :
= n nn n n n n n V V V Y Y Y Y Y Y Y Y Y I I I ˆ : ˆ ˆ ... : ... : : ... ... ˆ : ˆ ˆ 2 1 2 1 2 22 21 1 12 11 2 1 (2.24)
Notasi matrik dari Persamaan (2.24) adalah :
bus bus bus Y V I = (2.25) Dimana : = = nn n n n n bus Y Y Y Y Y Y Y Y Y Y ... : ... : : ... ... 2 1 2 22 21 1 12 11
2.3 Metode Aliran Daya (2,3)
Pada sistem multi-rel, penyelesaian aliran daya dengan metode Persamaan aliran daya. Metode yang digunakan pada umumnya dalam penyelesaian aliran daya, yaitu metode : Newton-Raphson, Gauss-Seidel, dan Fast Decoupled. Tetapi metode yang dibahas pada Tugas Akhir ini adalah metode Newton-Raphson.
2.3.1 Metode Newton-Raphson
Dalam metode Newton-Raphson secara luas digunakan untuk permasalahan Persamaan non-linear. Penyelesaian Persamaan ini menggunakan permasalahan yang linear dengan solusi pendekatan. Metode ini dapat diaplikasikan untuk satu Persamaan atau beberapa Persamaan dengan beberapa variabel yang tidak diketahui.
Untuk Persamaan non-linear yang diasumsikan memiliki sebuah variabel seperti Persamaan (2.27).
) (x
f
y= (2.27)
Persamaan (2.27) dapat diselesaikan dengan membuat Persamaan menjadi Persamaan (2.28).
0 ) (x =
f (2.28)
Menggunakan deret taylor Persamaan (2.28) dapat dijabarkan menjadi Persamaan (2.29).
( )
( )(
)
( )(
)
... ! 2 1 ! 1 1 ) ( 20 0 2 2 0 0 0 + − + − + = x x dx x df x x dx x df x f x f( )(
)
0 ! 1 0 0 − = + n n n x x dx x df n (2.29)Turunan pertama dari Persamaan (2.29) diabaikan, pendekatan linear menghasilkan Persamaan (2.30)
( )
( )(
)
0 ) ( 0 0 0 + − = = x x dx x df x f x f (2.30)Dari :
( )
( )
x dx df x f x x 0 0 0 1= − (2.31)Bagaimana pun, untuk mengatasi kesalahan notasi, maka Persamaan (2.31) dapat diulang seperti Persamaan (2.32).
( )
( )
x dx df x f x x (0) ) 0 ( ) 0 ( ) 1 ( = − (2.32)Dimana : x(0) = Pendekatan perkiraan X(1) = pendekatan pertama
Oleh karena itu, rumus dapat dikembangkan sampai iterasi terakhir (k+1), menjadi Persamaan (2.33).
( )
( )
x dx df x f x x k k k k ) ( ) ( ) ( ) 1 ( + = − (2.33)( )
( )
( ) ) ( ) ( ) 1 ( ' k k k k x f x f x x + = − (2.34) Jadi,( )
( )
( ) ) ( ' k k x f x f x=− ∆ (2.35) ) ( ) 1 (k k x x x= − ∆ + (2.36)Metode Newton-Raphson secara grafik dapat dilihat pada Gambar 2.8 ilustrasi metode Newton-Raphson.
Gambar 2.7 Ilustrasi metode Newton-Raphson
Pada Gambar 2.7 dapat dilihat kurva garis melengkung diasumsikan grafik Persamaan y=F(x). Nilai x pada garis x merupakan nilai perkiraan awal kemudian 0
dilakukan dengan nilai perkiraan kedua hingga perkiraan ketiga.
2.3.2 Metode Newton-Raphson dengan koordinat polar
Besaran-besaran listrik yang digunakan untuk koordinat polar, pada umumnya seperti Persamaan (2.37)
i i i V
V = ∠δ ; Vj =Vj ∠δj ; dan Yij = Yij∠θij (2.37)
Persamaan arus (2.21) pada Persamaan sebelumnya dapat diubah kedalam Persamaan polar (2.38).
∑
= = n j j ij i Y V I 1 j ij n j j ij i Y V I =∑
∠θ +δ =1 (2.38)Persamaan (2.38) dapat disubtitusikan kedalam Persamaan daya (2.22) pada Persamaan sebelumnya menjadi Persamaan (2.39).
i i i i jQ V I P − = * i i i V V* = ∠−δ Vi*= conjugate dari V i
j ij n j j ij i i i i jQ V Y V P − = ∠−δ
∑
∠θ +δ =1 j i ij n j j ij i i i jQ V Y V P − =∑
∠θ −δ +δ =1 (2.39) Dimana : ( )(
)
(
)
j i ij j i ij j j Cos e θij−δi+δj ≅ θ −δ +δ + θ −δ +δ sin (2.40)Persamaan (2.39) dan (2.40) dapat diketahui Persamaan daya aktif (2.41) dan Persamaan daya reaktif (2.42).
(
( ) ( ))
1 ) ( ) ( ) ( cos ij ik jk n j k j ij k i k i V Y V P =∑
θ −δ +δ = (2.41)(
( ) ( ))
1 ) ( ) ( ) ( sin ij ik jk n j k j ij k i k i V Y V Q =−∑
θ −δ +δ = (2.42)Persamaan (2.41) dan (2.42) merupakan langkah awal perhitungan aliran daya menggunakan metode Newton-Raphson. Penyelesaian aliran daya menggunakan proses iterasi (k+1). Untuk iterasi pertama (1) nilai k = 0, merupakan nilai perkiraan awal (initial estimate) yang ditetapkan sebelum dimulai perhitungan aliran daya.
Hasil perhitungan aliran daya menggunakan Persamaan (2.41) dan (2.42) dengan nilai Pi(k) dan Qi(k). Hasil nilai ini digunakan untuk menghitung nilai ∆Pi(k) dan ∆Qi(k).
Menghitung nilai ∆Pi(k) dan ∆Qi(k) menggunakan Persamaan (2.43) dan (2.44).
( ) ( )k calc i spec i k i p P P = , − , ∆ (2.43) ( ) ( )k calc i spec i k i Q Q Q = , − , ∆ (2.44) Hasil perhitungan (k) i P ∆ dan (k) i Q
∆ digunakan untuk matrik Jacobian pada Persamaan (2.45).
∆ ∆ ∆ ∆ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ = ∆ ∆ ∆ ∆ ) ( ) ( ) ( 2 ) ( 2 ) ( 2 ) ( ) ( 2 ) ( ) ( 2 2 ) ( 2 ) ( 2 2 ) ( 2 ) ( 2 ) ( ) ( 2 ) ( ) ( 2 2 ) ( 2 ) ( 2 2 ) ( 2 ) ( ) ( 2 ) ( ) ( 2 : : ... ... : : : : : : ... ... ... ... : : : : : : ... ... : : k n k n k k n k n k n n k n k n n k k n k k n k n k n n k n k n n k k n k k k n k k n k V V V Q V Q Q Q V Q V Q Q Q V P V P P P V P V P P P Q Q P P δ δ δ δ δ δ δ δ δ δ (2.45)
Persamaan (2.45) dapat dilihat bahwa perubahan daya berhubungan dengan perubahan besar tegangan dan sudut phasa.
Secara umum Persamaan (2.45) dapat disederhanakan menjadi Persamaan (2.46). ∆ ∆ = ∆ ∆ ) ( ) ( 4 3 2 1 ) ( ) ( k k k k V J J J J Q P δ (2.46)
Besaran elemen matriks Jacobian Persamaan (2.46) adalah : • J1
(
)
∑
≠ + − = ∂ ∂ i j k j k i ij ij k j k i k i i Y V V P ( ) ( ) ( ) ( ) ) ( sinθ δ δ δ (2.47)(
( ) ( ))
) ( ) ( ) ( sin ij ik jk ij k j k i k j i Y V V P θ δ δ δ =− − + ∂ ∂ i j ≠ (2.48) • J2(
( ) ( ))
) ( ) ( ) ( cos cos 2 ij ik jk i j ij k j ii ii k i k i i Y V Y V V P δ δ θ θ + − + = ∂ ∂∑
≠ (2.49)(
( ) ( ))
) ( ) ( cos ij ik jk ij k i k j i Y V V P θ δ δ + − = ∂ ∂ j ≠ i (2.50) • J3(
)
∑
≠ + − = ∂ ∂ i j k j k i ij ij k j k i k i i Y V V Q ( ) ( ) ( ) ( ) ) ( cosθ δ δ δ (2.51)(
( ) ( ))
) ( ) ( ) ( cos ij ik jk ij k j k i k j i Y V V Q δ δ θ δ =− − + ∂ ∂ i j ≠ (2.52) • J4(
)
∑
≠ + − − − = ∂ ∂ i j k j k i ij ij k j ii ii k i k i i Y V Y V V Q ( ) ( ) ( ) ( ) ) ( sin sin 2 θ θ δ δ (2.53)(
( ) ( ))
) ( ) ( sin ij ik jk ij k i k j i Y V V Q δ δ θ − + − = ∂ ∂ j ≠ i (2.54)Setelah nilai matrik Jacobian dimasukan kedalam Persamaan (2.46) maka nilai
) (k
i δ
∆ dan ∆V (ki ) dapat dicari dengan menginverskan matrik Jacobian seperti Persamaan (2.55). ∆ ∆ = ∆ ∆ − ) ( ) ( 1 4 3 2 1 ) ( ) ( k k k k Q P J J J J V δ (2.55) Setelah nilai (k) i δ ∆ dan (k) i V
∆ diketahui nilainya maka nilai ∆ (k+1)
i δ dan ) 1 ( + ∆ k i
V dapat dicari dengan menggunakan nilai ∆δi(k) dan ∆V (ki )ke dalam Persamaan (2.56) dan (2.57). ( ) ( ) ( )k i k i k i δ δ δ +1 = +∆ (2.56) ( ) ( ) ( )k i k i k i V V V +1 = +∆ (2.57)
Nilai δi(k+1) dan V (ik+1) hasil perhitungan dari Persamaan (2.56) dan (2.57) merupakan perhitungan pada iterasi pertama. Nilai ini digunakan kembali untuk perhitungan iterasi ke-2 dengan cara memasukan nilai ini ke dalam Persamaan (2.41) dan (2.42) sebagai langkah awal perhitungan aliran daya.
Perhitungan aliran daya pada iterasi ke-2 mempunyai nilai k = 1. Iterasi perhitungan aliran daya dapat dilakukan sampai iterasi ke-n. Perhitungan selesai apabila nilai (k) i P ∆ dan (k) i Q ∆ mencapai nilai 2,5.10-4.
Perhitungan aliran daya menggunakan metode Newton-Raphson 1. Membentuk matrik admitansi Yrel sistem
2. Menentukan nilai awal V(0), δ(0), Pspec, Qspec
3. Menghitung daya aktif dan daya reaktif berdasarkan Persamaan (2.41) dan (2.42)
4. Menghitung nilai ∆Pi(k) dan ∆Qi(k) beradasarkan Persamaan (2.43) dan (2.44) 5. Membuat matrik Jacobian berdasarkan Persamaan (2.46) sampai Persamaan
(2.54)
6. Menghitung nilai δ(k+1)
dan V(k+1) berdasarkan Persamaan (2.56) dan (2.57)
7. Hasil nilai δ(k+1) dan V(k+1) dimasukan kedalam Persamaan (2.41) dan (2.42) untuk mencari nilai ∆P dan Q∆ . Perhitungan akan konvergensi jika nilai ∆P dan Q∆ ≤ 10-4.
8. Jika sudah konvergensi maka perhitungan selesai, jika belum konvergensi maka perhitungan dilanjutkan untuk iterasi berikutnya.
2.4 Faktor Daya (5,6)
Dalam rangkaian listrik, biasanya terdapat tiga macam beban listrik yaitu beban resistif, beban induktif, dan beban kapasitif. Beban resistif adalah beban yang hanya terdiri dari tahanan ohm dan daya yang dikonsumsinya hanya daya aktif saja. Beban induktif mempunyai ciri–ciri bahwasanya disamping mengkonsumsi daya aktif, juga menyerap daya reaktif yang diperlukan untuk pembentukan medan magnet dalam beban
tersebut, jadi jumlah vektor dari daya reaktif (Q) dan daya aktif (P) biasa disebut daya buta (S). 2 2 Q P S= + ……….………..………...……… (2.58) φ Daya aktif (P) Daya reaktif (Q) Daya semu (S)
Gambar 2.8 Vektor Diagram Segitiga Daya
Dari gambar diatas didapat rumus untuk segi tiga daya :
P = V.I Cos φ (Watt) ; Q = V.I Sin φ ( Var) ; S = V.I (VA) Perbandingan antara daya aktif dan daya semu disebut faktor daya.
semu daya aktif daya daya faktor = S P Cosϕ = ………..……… (2.59)
Nilai faktor daya (Cos φ) yang besar, membawa pengaruh baik pada jaringan primer maupun sekunder. Makin besar daya reaktif suatu beban, maka makin kecil pula faktor dayanya.
Faktor daya (Cos φ) yang terbelakang terjadi pada kondisi dimana arus terbelakang terhadap tegangan dan keadaan ini dijumpai pada jaringan yang banyak terdapat beban induktif. Sebaliknya faktor daya yang terdahulu terjadi pada kondisi dimana arus mendahului tegangan dan keadaan ini dijumpai pada beban kapasitif.
2.5 Kapasitor Shunt (5,6)
Kapasitor ini terhubung paralel pada jaringan maupun langsung pada beban, dengan tujuan untuk perbaikan faktor daya, sebagai pengatur tegangan maupun untuk mengurangi kerugian daya dan tegangan pada jaringan (Deshpande, 1990).
Dengan anggapan tegangan sisi beban dipertahankan konstan, maka dari gambar dibawah ini terlihat bahwa dengan menggunakan kapasitor shunt, maka arus reaktif yang mengalir pada saluranakan berkurang. Hal ini menyebabkan berkurangnya penurunan tegangan pada saluran, sehingga diperlukan tegangan sumber yang tidak berbeda jauh dengan tegangan terima. Berkurangnya arus reaktif yang mengalir pada saluran akan memberikan penurunan rugi-rugi daya dan rugi-rugi energi.
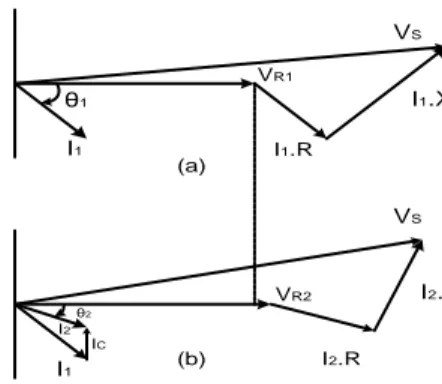
Pada Gambar 2.9. VR menunjukan tegangan pada sisi terima dan VS adalah
tegangan pada sisi pengirim. Dengan penambahan kapasitor shunt, kita juga dapat meningkatkan kapasitas penyaluran daya kepada konsumen, seperti yang terlihat pada Gambar 2.9 (b). VS I1.XS VR1 I1.R I1 θ1 I2.R I2.XS VS I1 I2 θ2 IC VR2 (a) (b)
Gambar 2.9 Tegangan Sebelum dan Sesudah Pemasangan Kapasitor Paralel
VR1 = VS – (IR.R+jIL.XS) ... (2.60)
VR2 = VS – (IR.R+jIL.XS – jIC.XS) ... (2.61)
∆VR = VR2 - VRI
= VS – (IR.R+jIL.XS – jIC.XS) – [ VS – (IR.R+jIL.XS – jIC.XS) ]
Keterangan :
IR = Komponen real arus (Ampere).
IL = Komponen reaktif arus lagging terhadap tegangan (Ampere).
IC = Komponen reaktif arus leading terhadap tegangan (Ampere).
R = Resistansi saluran (Ohm). XS = Reaktansi jaring (Ohm).
Ketika memasang kapasitor paralel, terjadi injeksi arus IC pada sistem sehingga
faktor daya meningkat dan IL berkurang. Hal itu mengakibatkan jatuhnya tegangan
berkurang IL x XS sehingga tegangan VR meningkat. Dari Persamaan (2.62), dijelaskan
bahwa tegangan kirim yang sama diperoleh tegangan terima yang lebih besar ketika sistem ditambahkan kapasitor paralel. Hal itu terjadi ketika faktor daya bus diperbaiki dengan menambah kapasitor paralel, tegangan terima bus juga meningkat. Untuk memperoleh hasil yang optimal, kekurangan daya reaktif yang dibutuhkan oleh beban sedapat mungkin dipenuhi oleh kapasitor paralel yang dipasang.
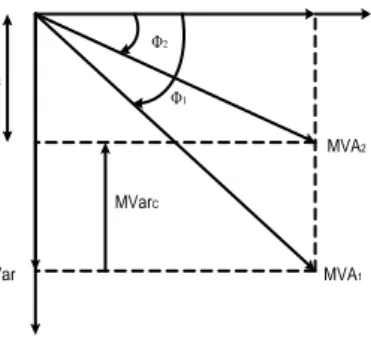
Φ2 Φ1 MVarC MVar MVA1 MVA2 MW MVar – MVarC
Gambar 2.10 Perbandingan Besar Daya Semu
Sebelum dan Sesudah Pemasangan Kapasitor Paralel.
MVA1 = MW – jMVar ... (2.63)
MVA2 = MW – jMVar - jMVarc ... (2.64)
∆MVA = MVA2 – MVA1
Keterangan :
MVA = Daya semu (Watt). MW = Daya aktif (Watt). MVar = Daya reaktif (Watt).
MVarc = Ijeksi daya reaktif dari kapasitor (Watt).
2.6 Bagaimana Kapasitor Memperbaiki Faktor Daya (5,6)
Sebagaiman diketahui membangkitkan daya reaktif pada pusat pembangkit tenaga dan menyalurkannya kepusat beban yang jaraknya jauh, sangatlah tidak ekonomis. Hal ini dapat diatasi dengan meletakan kapasitor pada pusat beban. Gambar berikut menunjukkan cara perbaikan faktor daya untuk sistem tersebut.
Seperti ditunjukan pada gambar, kapasitor menarik daya reaktif leading dan mensuplay daya reaktif lagging.
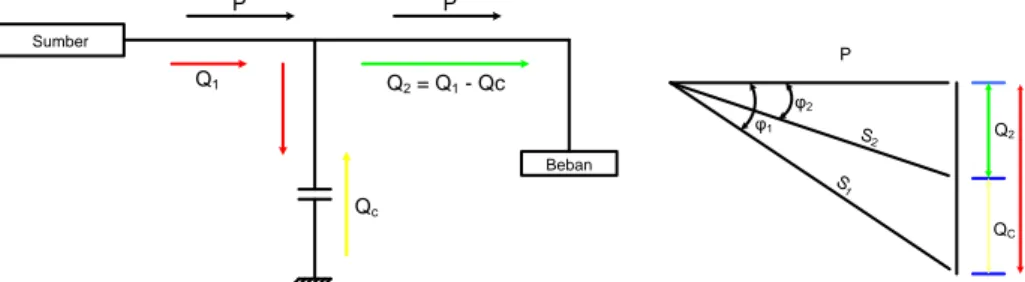
P P Q1 Qc Q2 = Q1 - Qc Sumber Beban Q1 Q2 QC S1 S2 P φ1 φ2 b a
Gambar 2.11 Perbaikan faktor daya dengan kapasitor
Anggap bahwa beban di suplay dengan daya nyata (P), daya reaktif (Q1), dan
daya semu (S1) pada faktor daya lagging sebesar :
1 S P Cosϕ =
(
)
1 2 2 1 2 1 Q P P Cos + = ϕ ………..………...……… (2.66)Bila kapasitor shunt sebesar Qc kVA dihubung ke beban, faktor daya akan diperbaiki dari cos φ1,cos φ2 dimana :
2 2 S P Cosϕ =
(
)
1 2 2 2 2 2 Q P P Cos + = ϕ ………..………....……… (2.67)(
)
[
]
1 2 2 2 1 2 Q Q P P Cos − + = ϕ ………...……..………… (2.68)Dari Gambar 2.11 dapat dilihat bahwa dengan daya reaktif sebesar Qc maka daya semu dan daya reaktif berkurang masing–masing dari S1 (kVA) ke S2 (kVA) dan
dari Q1 (kVAR) ke Q2 (kVAR). Dengan berkurangnya arus reaktif maka akan
mengurangi arus total, dan akhirnya mengurangi rugi–rugi daya.
Untuk menanggulangi masalah–masalah yang ditimbulkan beban induktif tersebut maka pada rangkaian listrik dengan beban induktif dipasang kapasitor daya paralel. Berikut ini ilustrasi bagaimana kapasitor membantu generator memberikan daya reaktif yang akan disuplay pada beban induktif.
2.7 Hubungan Kapasitor Dengan Daya Reaktif (6)
Daya aktif Daya reaktif
Generator Beban induktif
Keadaan tanpa kapasitor
Daya aktif
Generator Beban induktif
C Daya aktif
Keadaan dengan kapasitor
Gambar 2.12 Keadaan Tanpa dan Sesudah Pemasangan Kapasitor
Sebelum pemasangan kapasitor :
( ) I
(
pertiga fasa)
V
PR = 3 R L−L R cosΘR …...…....…… (2.69)
( ) I
(
pertiga fasa)
V
Setelah pemasangan kapasitor paralel sudut faktor daya pada jepitan beban berubah menjadi Θ΄R, Gambar 2.13.
PR = VR (L – N) IR cos ΘR C A B E Q R = V R (L – N) I R sin Θ R IR QC D VR (L – N) IR ΘR Θ'R
Gambar 2.13 Perbaikan Faktor Daya Dengan Kapasitor Paralel
Dari Gambar 2.13. dapat dituliskan : CA = PR tan ΘR per fasa
CD = PR tan Θ΄R per fasa
AD = QC = PR (tan ΘR - tan Θ΄R ) per fasa
Bila IC arus pada kapasitor statis :
(L N)
R C wC V
I = − ..………...…….………...… (2.71)
Jadi daya reaktif kapasitor adalah :
( ) 2 N L R C N L R C V I wC V Q = − = − .…..…………...… (2.72)
Dan besar kapasitor per fasa :
( )
(
)
( ) 2 1 1 tan tan N L R R R fasa R V w P C − Θ − Θ = ..……...………...… (2.73)Untuk tiga fasa maka daya reaktif total dari kapasitor :
( )
2
3 fasa 3QC wC VR L L
Q = = − ………..…..…...… (2.74)
atau besar kapasitor per fasa :
( ) 2 3 L L R fasa V w Q C − = ………..… (2.75)
Dari gambar terlihat akibat dari pemasangan kapasitor, beban induktif yang tenaga listrik disuplay oleh generator. Sebelum kapasitor terpasang daya aktif dan daya reaktif sepenuhnya disuplay dari generator, akibatnya daya semu (kapasitas) dari generator menjadi besar. Setelah kapasitor terpasang, seluruh atau sebagian besar dari daya reaktif yang diperlukan beban induktif disuplai oleh generator, dengan demikian tugas generator yang kini mensuplai daya aktif saja menjadi ringan, dengan demikian daya semu (kapasitasnya) menjadi kecil.