BAB I
PENDAHULUAN
I.1. Latar Belakang Masalah
Gerakan tanah akibat gempa bumi umumnya sangat tidak teratur dan hanya terjadi
beberapa detik sampai puluhan detik saja, walaupun kadang-kadang dapat terjadi lebih dari satu menit. Namun demikian gempa yang durasinya lebih dari satu menit ini sangat jarang terjadi, karena sifat getarannya yang acak dan tidak seperti beban statik pada umumnya maka efek beban gempa terhadap respon struktur tidaklah dapat diketahui dengan mudah. Oleh karena itu diperlukan usaha-usaha penyederhanaan agar model analisis pengaruh gempa terhadap respon struktur dapat diperhitungkan oleh kebanyakan insinyur. Gempa bumi umumnya direkam di permukaan tanah bebas (free field record) sedangkan fondasi bangunan terpendam di dalam tanah. Hasil penelitian para ahli menyimpulkan bahwa massa bangunan akan berpengaruh terhadap percepatan tanah di bawah bangunan yang bersangkutan (umumnya lebih kecil). Penyederhanaan yang dipakai adalah bahwa rekaman dari free field dianggap sebagai rekaman di bawah fondasi bangunan (foundatian input motion). Terdapat beberapa penyederhanaan untuk memperhitungkan efek gempa terhadap analisis struktur bangunan yaitu menggunakan Beban Ekivalen Statik, Spektrum Respon dan dengan Analisis Riwayat Waktu (Time History Analysis, THA).
Cara atau model analisis dengan menggunakan Spektrum Respon adalah pendekatan praktis. Spektrum ini pada hakekatnya adalah plot antara perioda getar struktur T lawan disain respon (umumnya aselerasi). Pada disain dengan prinsip “strength based” sebagaimana yang selama ini dianut di Indonesia, maka spektrum respon yang dimaksud adalah plot antara
Periode getar struktur T berhubungan dengan frekuensi alami f, dan frekuensi sudut ω (yang dikenal dengan eigenvalue). Jadi, perioda getar fundamental struktur T merupakan variabel yang sangat penting terhadap model analisis Spektrum Respon untuk mendapatkan nilai gaya geser dasar V.
Cara Beban Ekivalen Statik adalah suatu representasi dari beban gempa setelah disederhanakan dan dimodifikasi, dimana gaya inersia yang bekerja pada suatu massa akibat gempa disederhanakan menjadi Beban Ekivalen Statik. Beban Ekivalen Statik merupakan analisis dengan menggunakan mode pertama dari kemungkinan-kemungkinan mode suatu struktur bila terjadi goyangan. Mode merupakan pola/ragam goyangan struktur. Hal ini dikarenakan pada umumnya mode pertama akan menghasilkan perioda getar T yang signifikan untuk mewakili keseluruhan mode pada bangunan yang teratur. Periode getar T dari mode pertama ini disebut dengan periode getar alami fundamental.
Rakesh K. Goel dan Anil K. Chopra (1997)[1] mengevaluasi persamaan empiris untuk perhitungan periode getar alami fundamental bangunan yang didapatkan dari perilaku getaran alami bangunan yang diukur secara langsung dan direkam pada 8 gempa bumi yang terjadi di California, mulai dari 1971 gempa bumi San Fernando dan berakhir pada tahun 1994 gempa bumi Northridge. Ditunjukkan bahwa walaupun periode getar yang didapat dari persamaan empiris mempunyai nilai yang lebih pendek dibandingkan dengan periode terukur, persamaan-persamaan empiris ini dapat dikembangkan untuk mendapatkan hubungan yang lebih baik terhadap periode terukur (measured periods). Persamaan empiris untuk perhitungan periode getar fundamental bangunan struktur beton bertulang dan portal baja tersebut dikembangkan (dengan menambahkan penggunaan koefisien) dengan cara analisa regresi dari data periode bangunan terukur (measured period data). Namun, hasil perkembangan persamaan empiris yang didapat dengan cara analisa regresi ini tidak dapat digunakan untuk semua daerah gempa di dunia. Hal ini dikarenakan analisa yang dilakukan
tersebut adalah berada di California. Jadi persamaan empiris hasil analisa regresi tersebut boleh digunakan di daerah yang tingkat bahaya gempanya dibawah tingkat bahaya gempa daerah California namun tetap harus memerlukan evaluasi ulang yang teliti.
Khan Mahmud Amanat dan Ekramul Hoque (2006)[2] mengkaji perbedaan periode getar fundamental bangunan menggunakan cara analitis memakai model perhitungan komputasi terhadap dua kategori bangunan beton bertulang, yakni dengan memperhitungkan efek infill (komponen-komponen sekunder) dan tanpa memperhitungkan efek infill. Periode getar fundamental bangunan yang didapat memakai persamaan empiris yang disarankan oleh peraturan-peraturan (code) seperti UBC, NEHRP pada umumnya menunjukkan nilai periode yang lebih panjang dibandingkan periode yang teramati saat terjadi gempa. Untuk alasan inilah, di dalam peraturan ditetapkan suatu persamaan periode getar bangunan yang merupakan batasan maksimum periode getar fundamental. Hal ini pada kenyataannya tidak mendukung hasil perhitungan analitis dengan permodelan komputasi. Ternyata, pada umumnya desain dan analisa permodelan komputasi untuk struktur beton bertulang yang dilakukan secara konvensional mengijinkan struktur bergerak secara lebih fleksibel sehingga periode getar fundamental bangunan menjadi lebih panjang. Hal ini karena pada pemodelan komputasi konvensional tidaklah memperhitungkan efek komponen-komponen sekunder (infill). Pada kenyataannya, pertambahan massa dan kekakuan yang diberikan oleh komponen-komponen sekunder (infill) ini akan memperbesar kekakuan bangunan secara keseluruhan, yang akan berdampak pada nilai periode getar fundamental bangunan yang lebih pendek seperti yang teramati saat terjadi gempa.
Oh-Sung Kwon dan Eung Soo Kim (2010)[3] menjelaskan bahwa periode getar alami fundamental merupakan salah satu parameter terpenting dalam analisa beban gempa dengan cara ekivalen statik. Sedangkan nilai periode ini tergantung kepada massa dan kekakuan dari
bangunan. Hingga bangunan didisain, periode bangunan tidak dapat ditentukan. Namun justru nilai perioda ini diperlukan untuk melakukan analisa gempa untuk bangunan. Oleh sebab itu, beberapa dokumen peraturan bangunan struktur gempa merekomendasikan rumus empiris yang dapat digunakan untuk memperkirakan perioda bangunan hanya dengan sedikit informasi yang biasanya tersedia di awal perencanaan. Di dalam perancangan bangunan terhadap beban gempa, kebanyakan memakai persamaan empiris untuk perhitungan periode getar alami fundamental sebagai acuan perancangan. Berdasarkan NEHRP 00, 03, dan berdasarkan ASCE 7-02-05, nilai koefisien 𝐶𝑡 dan nilai koefisien 𝑥 di dalam rumus empiris periode getar fundamental bangunan masing-masing adalah 0.0446 dan 0.9 (untuk portal beton bertulang).
Persamaan empiris untuk memperkirakan waktu getar alami fundamental dari struktur frame dicantumkan di dalam peraturan SNI-1726-2010 adalah sebagai berikut:
𝑇 = 𝐶𝑡∙ ℎ𝑛𝑥 (1.1)
dimana : 𝑇 adalah waktu getar alami fundamental,
𝐶𝑡 adalah koefisien, 0.0466 untuk portal beton bertulang dan 0.0724 untuk portal baja,
ℎ𝑛 adalah tinggi bangunan dalam meter,
𝑥 adalah koefisien, 0.9 untuk portal beton bertulang dan 0.8 untuk portal baja. Sebagai alternatif, peraturan-peraturan tersebut di atas juga merekomendasikan rumus sederhana lain untuk menghitung waktu getar alami fundamental sebagai berikut:
Persamaan di atas hanya bisa digunakan untuk menghitung struktur dengan ketinggian tidak lebih dari 12 lantai dan tinggi tiap lantai tidak boleh kurang dari 3 meter.
I.2. Perumusan Masalah
Dalam tugas akhir ini, Penulis akan membandingkan beberapa parameter struktur yang dapat mempengaruhi perioda getar alami fundamental struktur bangunan. Model analisis berupa portal 2D akan dianalisis menggunakan metode analisis modal (analisis eigen value) untuk memperoleh periode mode pertama dari sturktur bangunan. Model analisis akan dikategorikan ke dalam tujuh kelompok untuk mempermudah pembahasan pada bab selanjutnya, yaitu:
1. Kategori 1 : struktur portal dengan jumlah lantai yang bervariasi Parameter : jumlah lantai bangunan
3x4m 6m 6x4m Portal 1.a 6m 6m 8x4m Portal 1.c Portal 1.b
Gambar 1.1. Portal Kategori 1
Parameter : jumlah bentangan bangunan
3x4m
4m 3x4m 6x4m
Portal 2.a Portal 2.b Portal 2.c
Gambar 1.2. Portal Kategori 2
3. Kategori 3 : struktur portal bentang tunggal dengan panjang bentang yang berbeda Parameter : panjang bentangan portal
3x4m
4m 8m
Portal 2.a
Portal 3
Gambar 1.3. Portal Kategori 3
4. Kategori 4 : struktur portal 3 bentangan dengan panjang bentang yang bervariasi Parameter : konfigurasi panjang bentang dari portal
3x4m Portal 4.a 6m 4m Portal 4.b 6m 3x4m Portal 2.b 6m 4m 4m
Gambar 1.4. Portal Kategori 4
5. Kategori 5 : struktur portal dengan ketidakteraturan kekakuan kolom antar lantai Parameter : struktur tidak beraturan akibat adanya lantai dengan ketinggian yang berbeda 6m
8x4m
Portal 1.c 6m5x5m
Portal 5.a7m
6m Portal 5.b7m
5x5m
Gambar 1.5. Portal Kategori 5
6m 6m
m 2m
Portal 1.a Portal 6.a
6m 8x4m Portal 1.b 6m m 2m Portal 6.b 3x4 m
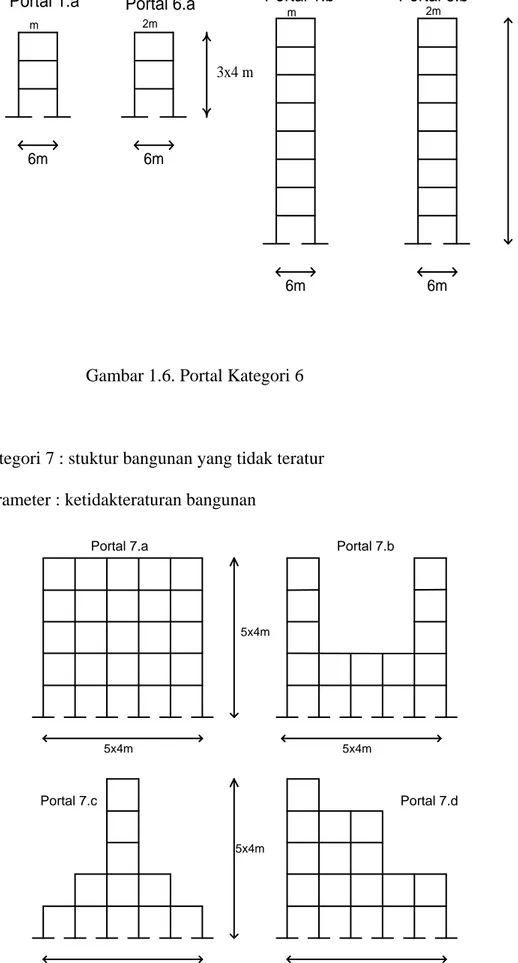
Gambar 1.6. Portal Kategori 6
7. Kategori 7 : stuktur bangunan yang tidak teratur Parameter : ketidakteraturan bangunan
5x4m
5x4m 5x4m
5x4m
5x4m
5x4m
Portal 7.a Portal 7.b
Gambar 1.7. Portal Kategori 7
Periode getar alami dari seluruh struktur diatas akan dihitung dengan melalui analisis eigen value dengan menggunakan bantuan program SAP2000.
I.3. Maksud dan Tujuan
Dalam tugas akhir ini penulis mempunyai maksud dan tujuan sebagai berikut :
“ Mengkaji pengaruh dari berbagai parameter terhadap waktu getar alami fundamental bangunan jenis rangka beton pemikul momen serta membandingkan waktu getar alami fundamental yang dihitung berdasarkan persamaan empiris yang dianjurkan di dalam SNI-1726-2010 dan dengan hasil analitis dengan menggunakan bantuan program SAP 2000 ”.
I.4. Pembatasan Masalah
Adapun pembatasan masalah yang diambil dalam penulisan tugas akhir ini, yakni :
a. Struktur bangunan yang dianalisis merupakan portal beton bertulang pemikul momen dua dimensi.
b. Peraturan pembebanan yang digunakan mengacu pada Tata Cara Perencanaan Pembebanan untuk Rumah dan Gedung tahun 1983.
c. Parameter variasi struktur bangunan yang akan dibandingkan adalah : 1. Jumlah lantai bangunan
2. Jumlah bentangan bangunan 3. Panjang bentang portal
4. Konfigurasi panjang bentang dari portal 5. Ketidakteraturan ketinggian tiap lantai 6. Ketidakteraturan massa
7. Ketidakteraturan bangunan
Metode yang digunakan dalam penulisan tugas akhir ini adalah mengumpulkan teori dan rumus – rumus untuk perhitungan dari buku-buku dan peraturan yang berhubungan dengan pembahasan pada tugas akhir ini, serta masukan dari dosen pembimbing.