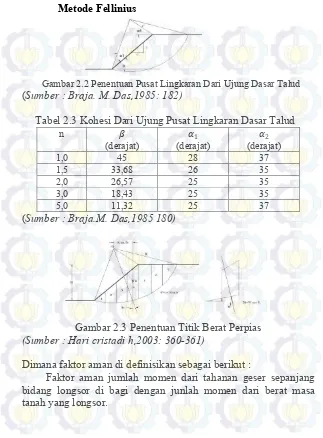
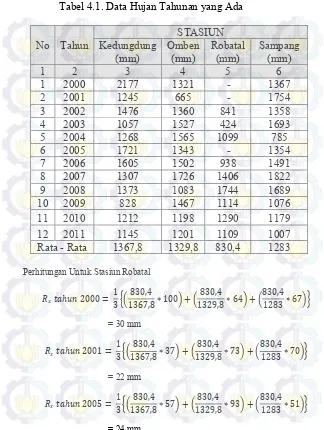
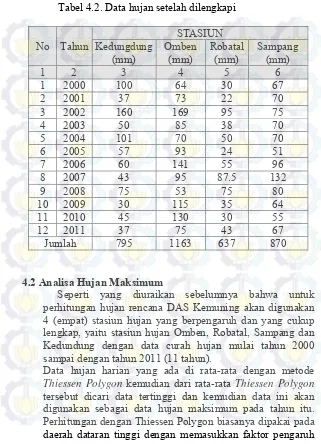
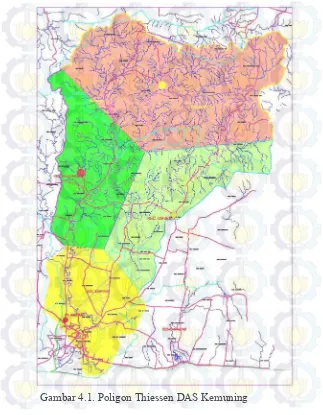
NORMALISASI KALI KEMUNING DENGAN CARA PENINGGIAN TANGKIS UNTUK MENGURANGI LUAPAN AIR DI KABUPATEN SAMPANG MADURA JAWA TIMUR
Teks penuh
Gambar



Dokumen terkait
2) Indonesia sebagai negara berkembang tentunya belum stabil dalam hal perekonomiannya, karena hal tersebut pemerintah melakukan kebijakan utang luar negeri. Tetapi
penelitian deskriptif analitik dengan pendekatan cross sectional.. dalam penelitian ini adalah ibu postpartum di Rumah Bersalin An Nissa Surakarta pada bulan Mei sampai Juni
Hasil percobaan dekontaminasi stainless steel terkontaminasi Cs-137 dengan silikon asetat dapat diketahui dari adanya penurunan aktivitas kontaminan sebelum dan sesudah
PERSEPSI KONSUMEN TERHADAP HARGA PSIKOLOGIS (Studi Kasus Pada Minimarket Indomaret Karangrejo I Semarang).. benar-benar merupakan
Fokus penelitian ini adalah untuk melihat pengaruh globalisasi terhadap akhlak remaja Muslim yang tinggal di tanah FELDA yang merupakan salah satu kelompok besar
Desentralisasi Fiskal dan Keuangan Daerah dalam Otonomi, Jakarta: Galia
Tujuan penelitian ini adalah menguji kinerja alat pengering hybrid tipe rak untuk pengeringan chip pisang kepok dengan tiga perlakuan yaitu pengeringan menggunakan
Tokoh politik negeri Johor Anak kampung Sungai Mengkuang Endau, Mersing, Taha bin Zakaria lahir pada tahun 1912, ayahnya haji Zakaria seorang pendakwah Islam berasal dari