Menyusun tabel pasanga nilai peubah dengan nilai fungsi Menggambar grafik fungsi dalam koordinat cartesius.

RENCANA PELAKSANAAN PEMBELAJARAN (RPP) Kelas VIII A

Nama Sekolah : SMP Negeri 1 Getasan Mata Pelajaran : Matematika

Kelas : VIII (Delapan)

Semester : 1 (Satu)

Alokasi Waktu : 8 x 40 menit (4 pertemuan).

A. Standar Kompetensi: FUNGSI

Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus.

B. Kompetensi Dasar:

Membuat sketsa grafik fungsi aljabar sederhana pada sistem koordinat cartesius.

C. Indikator

 Menyusun tabel pasanga nilai peubah dengan nilai fungsi

 _{Menggambar grafik fungsi dalam koordinat} cartesius.

 Karakter siswa yang diharapkan :

- Disiplin ( Discipline )

- Rasa hormat dan perhatian( respect) - Tekun( diligence )

- Tanggungjawab( responsibility) D. Materi Ajar

Menggambar Grafik fungsi

Gambar grafik suatu fungsi dalam koordinat Cartecius dapat diperoleh dengan langkah-langkah berikut:

1. Menentukan pasangan berurutan fungsi tersebut.

2. Menggambarkan pasangan berurutan sebagai titik dalam koordinat Cartecius

E. Model Pembelajaran

Model pembelajaran kooperatif, tanya jawab, dan pemberian tugas.

 _{Model pembelajaran kooperatif adalah model} pembelajaran yang diupayakan untuk dapat meningkatkan peran serta siswa, memfasilitas isiswa dengan pengalaman sikap kepemimpinan dan membuat keputusan dalam kelompok, serta memberikan kesempatan kepada para siswa untuk berinteraksi dan belajar secara bersama meskipun mereka berasal dari berbagai latarbelakang yang berbeda. Berikut tahap dalam penerapan model pembelajaran kooperatif :

FASE-FASE INDIKATOR TINGKAH LAKU GURU

Fase 1

Menyampaikan tujuan dan memotivasi siswa

Menyampaikan semua tujuan pembelajaran yang ingin dicapai dan

memotivasi siswa untuk aktif belajar.

Fase 2 Menyajikaninfor_masi

Menyajikan materi ajar kepada siswa dengan jalan mendemonstrasikan atau melalui bahan bacaan.

Fase 3 Mengorganisasik an siswa kedalam kelompok-kelompok belajar

Menjelaskan kepada siswa bagaimana cara membentuk kelompok belajar . Fase 4 Membimbing kelompok belajar Membimbing setiap kelompok belajar untuk belajar dan bekerja.

Fase 5 Evaluasi Mengevaluasi hasil belajardan kerja masing-masing kelompok.

Fase 6 Memberikan_penghargaan

Guru memberikan penghargaan pada para siswa baik sebagai individu maupun kelompok, baik karena usaha yang telah merekalakukan maupun karena hasil yang telah merka capai.

Dalam pelaksanaan fase diatas guru

menggunakan pendekatan pembelajaran tipe STAD yaitu tipe pembelajaran yang terbentuk dari sebuah kelompok serta terdiri dari empat atau lima siswa yang mewakili heterogenitas kelas ditinjau dari kinerja, suku dan jenis kelamin.

 _{Tanya jawab adalah metode dimana siswa} diberikan kesempatan untuk bertanya ketika menemui kesulitan dalam pemahaman materi.  Pemberian Tugas adalah agar siswa mengulang

lagi materi yang telah disampaikan dan sebagai indikator apakan siswa tersebut mampu memahami materi yang telah disampaikan.

F. Langkah-langkah Kegiatan pertemuan 1-4

Pendahuluan :

 Memotivasi siswa agar dapat mengerjakan soal-soal dengan baik berkaitan dengan materi mengenai fungsi, menggambar grafik fungsi.

 Guru menjelaskan tentang metode belajar yang akan digunakan (STAD)

Kegiatan Inti:

 _Eksplorasi

Dalam kegiatan eksplorasi, guru:

 Menggunakan beragam pendekatan

pembelajaran, media pembelajaran, dan sumber belajar lain;

 memfasilitasi terjadinya interaksi antarpeserta didik serta antara peserta didik dengan guru, lingkungan, dan sumber belajar lainnya;

 _{melibatkanpesertadidiksecaraaktifdalamsetiapke} giatanpembelajaran;

 Elaborasi

Dalam kegiatan elaborasi, guru:

 Guru membagi siswa dalam kelompok yang terdiri dari lima siswa, dan mewakili heterogenitas kelas ditinjau dari kinerja, suku dan jenis kelamin. Kemudian siswa ditempatkan sesuai dengan kelompoknya.

 _{Masing-masing kelompok mendapat jumlah soal} sebanyak 10, setiap siswa mengerjakan 2 soal;  _{Guru mengamati dan membimbing kerjasama}

dalam kelompok;

 memfasilitasi peserta didik berkompetisi secara sehat untuk meningkatkan prestasi belajar;  memfasilitasi peserta didik membuat laporan

eksplorasi yang dilakukan baik lisan maupun tertulis, secara individual maupun kelompok;  memfasilitasi peserta didik untuk menyajikan

hasil kerja individual maupun kelompok;  _Konfirmasi

Dalam kegiatan konfirmasi, guru:

 memberikan umpan balik positif dan penguatan dalam bentuk lisan, tulisan, isyarat, maupun hadiah terhadap keberhasilan peserta didik,  memberikan konfirmasi terhadap hasil

eksplorasi dan elaborasi peserta didik melalui berbagai sumber,

 _{memfasilitasi peserta didik melakukan refleksi} untuk memperoleh pengalaman belajar yang telah dilakukan,

 _{memfasilitasi peserta didik untuk memperoleh} pengalaman yang bermakna dalam mencapai kompetensi dasar:

 berfungsi sebagai narasumber dan fasilitator dalam menjawab pertanyaan peserta didik yang menghadapi kesulitan, dengan menggunakan bahasa yang baku dan benar;  membantu menyelesaikan masalah;

 memberi acuan agar peserta didik dapat melakukan pengecekan hasil eksplorasi;  memberi informasi untuk bereksplorasi lebih

jauh;

 memberikan motivasi kepada peserta didik yang kurang atau belum berpartisipasi aktif. Kegiatan Akhir :

Dalam kegiatan penutup, guru:

 bersama-sama dengan peserta didik dan/atau

sendiri membuat rangkuman/simpulan

pelajaran;

 melakukan penilaian dan/atau refleksi terhadap kegiatan yang sudah dilaksanakan secara konsisten dan terprogram;

 memberikan umpan balik terhadap proses dan hasil pembelajaran;

 merencanakan kegiatan tindak lanjut dalam bentuk pembelajaran remedi, program pengayaan, layanan konseling dan/atau memberikan tugas baik tugas individual maupun kelompok sesuai dengan hasil belajar peserta didik.

G. Alat dan Sumber Belajar

Sumber :

- Buku paket, yaitu buku Matematika Kelas VIII Semester 1.

H. Penilaian Hasil Belajar Indikator

Pencapaian Kompetensi

Penilaian Teknik BentukInstru

men Instrumen/ Soal

1. Menyusu tabel pasangan nilai peubah dengan nilai fungsi 2.Menggam bar grafik fungsi pada koordinat Cartesius Tes

tertulis singkatIsian Uraian

1.Diketahui f(x) = 2x + 3.

Lengkapilah tabel berikut:

X 0 1 2 3

f(x) .. .. .. ..

2.Dengan menggunakan tabel

gambarlah grafik fungsi yang dinyatakan f(x) = 3x -2.

3.Diketahui himpunan P =



2, 3, 4, 5



dan Q =

 

2, 3 . Relasi dari P ke Q adalah l “lebih dari“.

a. Gambarlah diagram panah relasi itu! Apakah relasi itu merupakan fungsi? b. Buatlah himpunan pasangan berurutannya! c. Gambarlah diagram Cartesiusnya! 4.Diketahui f(x): x2 3, dengan domain {-2, -1, 0, 1, 2, 3}. Tentukan range fungsi tersebut dan gambarkan grafik fungsinya!

Kunci jawaban:

1. f(x):2x + 3

X 0 1 2 3

2. Gambar grafik

F(x): 3x – 2

3. A. Gambar panah relasi

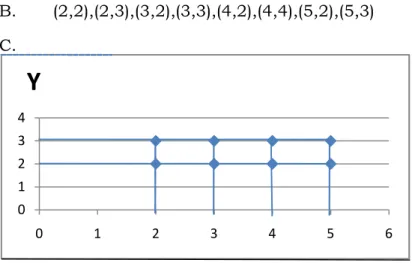
Bukan sebuah fungsi karena tidak berpasangan satu-satu. B. (2,2),(2,3),(3,2),(3,3),(4,2),(4,4),(5,2),(5,3) C. -10 -5 0 5 10 -4 -2 0 2 4

f(x): 3x - 2

0 1 2 3 4 0 1 2 3 4 5 6

Y

2 3 4 5 2 3

4. Range: {1,-2,-3,-2,1,6}

Grafik fungsi kuadrat f(x): x2 3

-4 -2 0 2 4 6 8 -4 -2 0 2 4

f(x): X

2

_{- 3}

RENCANA PELAKSANAAN PEMBELAJARAN (RPP) Kelas VIII F

Nama Sekolah : SMP Negeri 1 Getasan Mata Pelajaran : Matematika

Kelas : VIII (Delapan)

Semester : 1 (Satu)

Alokasi Waktu : 8 x 40 menit (4 pertemuan).

A. Standar Kompetensi: FUNGSI

Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus.

B. Kompetensi Dasar:

Membuat sketsa grafik fungsi aljabar sederhana pada sistem koordinat cartesius.

C. Indikator

 Menyusun tabel pasanga nilai peubah dengan nilai fungsi

 _{Menggambar grafik fungsi dalam koordinat} cartesius.

 Karakter siswa yang diharapkan :

- Disiplin ( Discipline )

- Rasa hormat dan perhatian( respect) - Tekun( diligence )

- Tanggungjawab( responsibility) D. Materi Ajar

Menggambar Grafik fungsi

Gambar grafik suatu fungsi dalam koordinat Cartecius dapat diperoleh dengan langkah-langkah berikut:

3. Menentukan pasangan berurutan fungsi tersebut.

4. Menggambarkan pasangan berurutan sebagai titik dalam koordinat Cartecius

E. Model Pembelajaran

Model pembelajaran kooperatif, tanya jawab, dan pemberian tugas.

 _{Model pembelajaran kooperatif adalah model} pembelajaran yang diupayakan untuk dapat meningkatkan peran serta siswa, memfasilitas isiswa dengan pengalaman sikap kepemimpinan dan membuat keputusan dalam kelompok, serta memberikan kesempatan kepada para siswa untuk berinteraksi dan belajar secara bersama meskipun mereka berasal dari berbagai latarbelakang yang berbeda. Berikut tahap dalam penerapan model pembelajaran kooperatif :

FASE-FASE INDIKATOR TINGKAH LAKU GURU

Fase 1

Menyampaikan tujuan dan memotivasi siswa

Menyampaikan semua tujuan pembelajaran yang ingin dicapai dan

memotivasi siswa untuk aktif belajar.

Fase 2 Menyajikaninfor_masi

Menyajikan materi ajar kepada siswa dengan jalan mendemonstrasikan atau melalui bahan bacaan.

Fase 3 Mengorganisasik an siswa kedalam kelompok-kelompok belajar

Menjelaskan kepada siswa bagaimana cara membentuk kelompok belajar . Fase 4 Membimbing kelompok belajar Membimbing setiap kelompok belajar untuk belajar dan bekerja.

Fase 5 Evaluasi Mengevaluasi hasil belajardan kerja masing-masing kelompok.

Fase 6 Memberikan_penghargaan

Guru memberikan penghargaan pada para siswa baik sebagai individu maupun kelompok, baik karena usaha yang telah merekalakukan maupun karena hasil yang telah merka capai.

Dalam pelaksanaan fase diatas guru menggunakan pendekatan pembelajaran kooperatif tipe NHT, yaitu suatu model pembelajaran dimana siswa dalam kelompok kecil terdiri dari 4-6 orang, yang mana siswa belajar dan bekerja secara kolaboratif dengan struktur kelompok yang heterogen. Tujuan pembelajaran kooperatif adalah untuk meningkatkan partisipasi siswa dan mempersiapkan siswa agar memiliki sifat kepemimpinan.

 Tanya jawab adalah metode dimana siswa diberikan kesempatan untuk bertanya ketika menemui kesulitan dalam pemahaman materi.  Pemberian Tugas adalah agar siswa mengulang

lagi materi yang telah disampaikan dan sebagai indikator apakan siswa tersebut mampu memahami materi yang telah disampaikan.

G. Langkah-langkah Kegiatan pertemuan 1-4

Pendahuluan :

 Memotivasi siswa agar dapat mengerjakan soal-soal dengan baik berkaitan dengan materi mengenai fungsi, menggambar grafik fungsi.

 Guru menjelaskan tentang metode belajar yang akan digunakan (NHT)

Kegiatan Inti:  _Eksplorasi

Dalam kegiatan eksplorasi, guru:

 Menggunakan beragam pendekatan

pembelajaran, media pembelajaran, dan sumber belajar lain;

 memfasilitasi terjadinya interaksi antarpeserta didik serta antara peserta didik dengan guru, lingkungan, dan sumber belajar lainnya;

 _{melibatkanpesertadidiksecaraaktifdalamsetiapke} giatanpembelajaran;

 Elaborasi

Dalam kegiatan elaborasi, guru:

 Guru membentuk kelompokNumbered Head

Together yang heterogen yang sesuai dengan

nilai pre-tes, setiap kelompok terdiri dari lima siswa. Kemudian siswa ditempatkan sesuai dengan kelompoknya.

 Setiap siswa dalam tiap kelompok mendapa nomor 1-5 dan member nama kelompok yang berbeda.

 Siswa diberi kartu soal untuk dikerjakan dikelompok masing-masing. Tiap kelompok mendapatkan 10 kartu soal dan setiap siswa mengerjakan 2 kartu soal.

 _{Guru mengamati dan membimbing kerjasama} dalam kelompok;

 Guru memanggil salah satu nomor dan siswa yang nomornya dipanggil mengangkat tangan,

kemudian siswa yang ditunjuk guru

mengerjakan di papan tulis.

 _{Demikian seterusnya hingga semua kartu soal} terjawab dan maing-masing kelompok dapat menerangkannya.

 _{memfasilitasi peserta didik berkompetisi secara} sehat untuk meningkatkan prestasi belajar;  _{memfasilitasi peserta didik membuat laporan}

eksplorasi yang dilakukan baik lisan maupun tertulis, secara individual maupun kelompok;

 _{memfasilitasi peserta didik untuk menyajikan} hasil kerja individual maupun kelompok;

 _Konfirmasi

Dalam kegiatan konfirmasi, guru:

 memberikan umpan balik positif dan penguatan dalam bentuk lisan, tulisan, isyarat, maupun hadiah terhadap keberhasilan peserta didik,  memberikan konfirmasi terhadap hasil

eksplorasi dan elaborasi peserta didik melalui berbagai sumber,

 memfasilitasi peserta didik melakukan refleksi untuk memperoleh pengalaman belajar yang telah dilakukan,

 memfasilitasi peserta didik untuk memperoleh pengalaman yang bermakna dalam mencapai kompetensi dasar:

 berfungsi sebagai narasumber dan fasilitator dalam menjawab pertanyaan peserta didik yang menghadapi kesulitan, dengan menggunakan bahasa yang baku dan benar;  membantu menyelesaikan masalah;

 memberi acuan agar peserta didik dapat melakukan pengecekan hasil eksplorasi;  memberi informasi untuk bereksplorasi lebih

jauh;

 memberikan motivasi kepada peserta didik yang kurang atau belum berpartisipasi aktif.

Kegiatan Akhir :

Dalam kegiatan penutup, guru:

 _{bersama-sama dengan peserta didik dan/atau}

sendiri membuat rangkuman/simpulan

pelajaran;

 melakukan penilaian dan/atau refleksi terhadap kegiatan yang sudah dilaksanakan secara konsisten dan terprogram;

 _{memberikan umpan balik terhadap proses dan} hasil pembelajaran;

 merencanakan kegiatan tindak lanjut dalam

bentuk pembelajaran remedi, program

pengayaan, layanan konseling dan/atau memberikan tugas baik tugas individual maupun kelompok sesuai dengan hasil belajar peserta didik.

G. Alat dan Sumber Belajar

Sumber :

- Buku paket, yaitu buku Matematika Kelas VIII Semester 1.

- Buku referensi lain.

H. Penilaian Hasil Belajar Indikator

Pencapaian Kompetensi

Penilaian Teknik BentukInstru

men Instrumen/ Soal

3. Menyusu tabel pasangan nilai peubah dengan nilai fungsi 4.Menggam bar grafik fungsi pada koordinat Cartesius Tes

tertulis singkatIsian Uraian

5.Diketahui f(x) = 2x + 3.

Lengkapilah tabel berikut:

X 0 1 2 3

f(x) .. .. .. ..

6.Dengan menggunakan tabel

gambarlah grafik fungsi yang dinyatakan f(x) = 3x -2.

7.DiketahuihimpunanP =



2, 3, 4, 5



dan Q =

 

2, 3 . Relasi dari P ke Q adalah l “lebih dari“.

d. Gambarlah diagram panah relasi itu! Apakah relasi itu merupakan fungsi?

e. Buatlah himpunan pasangan berurutannya!

f. Gambarlah diagram Cartesiusnya!

8.Diketahuif(x): x2 3,dengan domain {-2, -1, 0, 1, 2, 3}. Tentukan range fungsi tersebut dan gambarkan grafik fungsinya! Kunci jawaban: 3. f(x):2x + 3 X 0 1 2 3 f(x) 3 5 7 9 4. Gambar grafik F(x): 3x – 2

5. A. Gambar panah relasi

Bukan sebuah fungsi karena tidak berpasangan satu-satu. -10 -5 0 5 10 -4 -2 0 2 4

f(x): 3x - 2

2 3 2 3 4 5

B. (2,2),(2,3),(3,2),(3,3),(4,2),(4,4),(5,2),(5,3) C.

6. Range: {1,-2,-3,-2,1,6}

Grafik fungsi kuadrat f(x): x2 3 0 1 2 3 4 0 1 2 3 4 5 6

Y

-4 -2 0 2 4 6 8 -4 -2 0 2 4

f(x): X

2

_{- 3}

Lembar Soal Pretes dan Postes Nama:

Kelas:

1. Pada sebuah fungsi, daerah yang semua anggotanya harus berpasangan adalah…

a. domain b. kodomain

c. domain dan kodomain d. domain dan range 2. Diketahui himpunan pasangan berurutan dari

suatu pemetaana dalah {(a,3), (d,2), (c,1), (b,4)}. Domain dari pemetaan tersebuta dalah…

a. {1,2,3} b. {1,2,3,4} c. {a,b,c} d. {a,b,c,d} 3. Diketahui suatu pemetaan dari himpunan A

kehimpunan B. Jika n(A) = 3 dan n(B) = 4, maka banyak pemetaan yang mungkin adalah…

a. 12 b. 24 c. 32 d. 64

4. Banyak anggota dari daerah hasil (range) suatu relasi yang dinyatakan dengan {3,9), 2,4), (-1,1), (2,4), (3,9)} adalah ….

a. 3 b. 4 c. 5 d. 6

5. Suatu fungsi dirumuskan sebagai f(x) pxq. Jikaf (-1) = 2 dan f (-2) = 4, maka nilai f(-3) adalah…

a. 6 b. 8 c. 10 d. 15

6. Diketahui himpunan pasangan berurutan dari suatu pemetaan adalah {(p,3), (q,2), (r,1), (s,4)}. Domain dari pemetaan tersebut adalah…

7. Banyak anggota dari daerah hasil(range) suatu relasi yang dinyatakan dengan {(-2,8),(-1,1), (2,8)} adalah ….

a. 1 b. 2 c. 3 d. 4

8. Diketahui suatu pemetaan dari himpunan A kehimpunan B. Jika n(A) = 2 dan n(B) = 3, maka banyak pemetaan yang mungkin adalah…

b. 9 b. 6 c. 12 d. 5

9. Suatu fungsi dirumuskan sebagai f(x) pxq. Jika f (-2) = 3 dan f(4) = 5, maka nilai f(-5) adalah…

b. 6 b. -8 c. -10 d. 15

10. Suatu fungsi dirumuskan sebagai

. )

(x ax b

f   Jika f(-5) = 4 dan f(2) = 3, maka nilai f(7) adalah…

a. 2 b. 7 c. -7 d. -2

Nilai Pretes dan Postes Kelas VIII A

no nama nilai nilai

pretes postes

1 Andrean H. S 70 70

2 Aprilia Kartika Dewi 70 90

3 Arta Dewi Boru. S 80 80

4 Eko Pambudi 20 100

5 Eko Wahono 70 70

6 Giyarni 60 90

7 Hizkia Krsipratama 80 90

8 Indah Sari 90 80

9 Irene Tammy Gracia M 20 100

10 Krismanto 90 90

11 Listya 10 100

12 Luluk Putri Hapsari 90 90

13 Martin Kurniasari 30 90 14 Mella Anggraeni 70 80 15 Mukhalim Ramadhan 30 90 16 Nur Prihatini 100 100 17 Nurhayati 80 90 18 Nuryani 50 90 19 Peni W 80 80 20 Prio 80 100

21 Pungky Dwi Aji W 80 80

22 Rima Tesalonika 70 80

23 Riski 40 100

24 Riyan. S 70 80

25 Santo 60 90

26 Sella Ayunda D 70 70

27 Septian Ardi Saputro 20 100

28 Septiyanto 40 80

29 Sinta. N 90 100

30 Sri Astuti 70 70

31 Widi Astuti 60 100

Nilai Pretes dan Postes Kelas VIII F

no Nama _PretesNilai _PostesNilai

1 Ali Sodiqin 70 80

2 Alwi. N 70 70

3 Andika Fendi Pratama 50 70

4 Arif. T 40 70

5 Ayom Tri Astuti 60 70

6 Basuki 70 70

7 Beti Cahyaningsih 70 60

8 Danu Renmi W 60 70

9 Edi Sulistyo 70 80

10 Eisa resti Anindita 60 70

11 Fadil Bayu Laksono 70 80

12 Fahrulloh Muftarika Yusuf 70 70

13 Fitri Wulan Dini 50 60

14 Geffi Putri M 70 70

15 Hasdiwijaya 60 80

16 Imam 80 80

17 Intan Nur Aini 60 70

18 Jihad Hutomo Mukti 70 100

19 Jihan Fadhillah 80 100

20 Nur Arinda 70 80

21 Puri R.A 60 70

22 Putri Wulan Sari 80 80

23 Rizal A.N.S 70 70 24 Rizka. D 40 60 25 Rudi prasetya 40 90 26 Saroyah 60 70 27 Septia A.P 70 70 28 Siti Marliyah 40 70 29 Slamet Rahayu 50 70 30 Sriyanti 50 60 31 Wahyu. A 40 70 32 Yusworo 60 60

LEMBAR KERJA SISWA KELAS VIII A

Mata Pelajaran : Matematika

Kelas/Semester : VIII(delapan/1)

Standar Kompetensi : 1. Memahami betul aljabar, relasi, fungsi dan

persamaan garis lurus. Kompetensi Dasar : 1.5 Membuat sketsa grafik

fungsi aljabar sederhana pada sistem koordinat cartesius.

Indikator : 1. Menentukan nilai fungsi

2. Menggambar grafik fungsi dalam koordinat cartesius

Alokasi Waktu : 30 menit.

Kegiatan Inti:

A. Diketahui suatu fungsi f : x  3x + 2, maka tentukan :

a. Rumus fungsinya;

b. Range/daerah hasil fungsi tersebut dan

pasangan berurutan jika domain fungsinya {x | -3  x  3};

c. Buat diagram cartesius jika domain-nya sama dengan b;

d. Bayangan dari – 4 ; e. Prapeta dari -1;

Jawab: . f : x  3x + 2

a. Rumus fungsi f(x) = …x + …

b. Domain {x | -3 x  3} sehingga domainnya {3, -2, -1, 0, 1, -2, 3}  f(-3) = 3(-3) + 2 = -7  f(-2) = 3(…) + … = …  f(-1) = 3(…) + … = …  f(0) = 3(…) + … = …  f(1) = 3(…) + … = …  f(2) = 3(…) + … = …  f(3) = 3(…) + … = …

jadi, range-nya adalah {-7,…,…,…,…,…,…} Pasangan berurutan {(-3,-7), (…,…), (…,…),

(…,…), (…,…), (…,…), (…,…)} c. Diagram cartesius

= … + … = …

e. prapeta dari -1 atau f(x) = -1 f (x) = -1 …x +…= -1 …..x = …+…

x = …

Nama anggota Kelompok:

1. 2.

3. 4.

LEMBAR KERJA SISWA KELAS VIII F

Mata Pelajaran : Matematika

Kelas/Semester : VIII (delapan/1)

Standar Kompetensi : 1. Memahami bentuk aljabar, relasi, fungsi dan

persamaan garis lurus. Kompetensi Dasar : 1. Membuat sketsa grafik

fungsi aljabar sederhana pada sistem koordinat cartesius.

Indikator : 1.Membuat tabel pasangan

nilai peubah dengan nilai suatu fungsi.

2. Membuat himpunan pasangan berurutan

3. Menggambar grafik fungsi dan koordiat cartesius.

Alokasi Waktu : 30 menit.

1. Suatu fungsi f(x) = 2x + 1, dengan domain A = {x|-1 x2, xR}

a. Buatlah table fungsi dan tulislah daerah hasilnya.

b. Himpunan pasangan berurutan c. Buat diagram cartesiusnya d. Peta dari 4

Penyelesaian: a. Table fungsi

Domain A = {x|-1 x2, xR} dapat dinyatakan dengan mendaftarkan anggota A = {-1, …, …, 2} x -1 … … 2 2x 2 x (-1)= -2 2 x … = … 2 x … = … 2 x 2 = … 1 1 1 1 1 f(x) -2+1= -1 … + 1 =…. … + 1 =…. … + 1 =…. [x, f(x)] (-1, -1) (…,...) (…,...) (2, ...) Daerah hasil = { -1,…,…,…}. (lihat pada

baris ke empat)

b. Himpunan pasangan berurutan sebagai berikut : { (-1,-1), (…,…), (…,…), (…,…)} c. Diagram cartesiusnya:

d. Prapeta dari 4 atau f(x) = 4 2x + 1 = 4

2x = 4 + ( … ) 2x = … x = …

2. Suatu fungsi f(x) = 2x + 1, dengan domain A = {x|1 x4, xR}

a. Buatlah table fungsi dan tulislah daerah hasilnya.

b. Himpunan pasangan berurutan c. Buat diagram cartesiusnya d. Peta dari 5

Penyelesaian: a. Table fungsi

Domain A = {x|1 x4, xR} dapat dinyatakan dengan mendaftarkan anggota A = {1, …, …, 4} x 1 … … 4 2x 2 x 1 =2 2 x … = … 2 x … = … 2 x 2 = … 1 1 1 1 1 f(x) 2+1= 3 … + 1 =…. … + 1 =…. … + 1 =…. [x, f(x)] (1, 3) (…,...) (…,...) (4, ...) Daerah hasil = {3,…, …,…}. (lihat pada

baris ke empat)

b. Himpunan pasangan berurutan sebagai berikut : { (1,3), (…,…), (…,…), (…,…)} c. Diagram cartesiusnya:

d. Prapeta dari 5 atau f(x) = 5 2x + 1 = 5

2x = 5 + ( … ) 2x = … x = … Nama Anggota Kelompok:

1) 2) 3) 4) 5)

Pr df 0.25 0.50 0.10 0.20 0.05 0.10 0.025 0.050 0.01 0.02 0.005 0.010 0.001 0.002 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 0.68052 0.68038 0.68024 0.68011 0.67998 0.67986 0.67975 0.67964 0.67953 0.67943 0.67933 0.67924 0.67915 0.67906 0.67898 0.67890 0.67882 0.67874 0.67867 0.67860 0.67853 0.67847 0.67840 0.67834 0.67828 0.67823 0.67817 0.67811 0.67806 0.67801 0.67796 0.67791 0.67787 0.67782 0.67778 0.67773 0.67769 0.67765 0.67761 0.67757 1.30254 1.30204 1.30155 1.30109 1.30065 1.30023 1.29982 1.29944 1.29907 1.29871 1.29837 1.29805 1.29773 1.29743 1.29713 1.29685 1.29658 1.29632 1.29607 1.29582 1.29558 1.29536 1.29513 1.29492 1.29471 1.29451 1.29432 1.29413 1.29394 1.29376 1.29359 1.29342 1.29326 1.29310 1.29294 1.29279 1.29264 1.29250 1.29236 1.29222 1.68288 1.68195 1.68107 1.68023 1.67943 1.67866 1.67793 1.67722 1.67655 1.67591 1.67528 1.67469 1.67412 1.67356 1.67303 1.67252 1.67203 1.67155 1.67109 1.67065 1.67022 1.66980 1.66940 1.66901 1.66864 1.66827 1.66792 1.66757 1.66724 1.66691 1.66660 1.66629 1.66600 1.66571 1.66543 1.66515 1.66488 1.66462 1.66437 1.66412 2.01954 2.01808 2.01669 2.01537 2.01410 2.01290 2.01174 2.01063 2.00958 2.00856 2.00758 2.00665 2.00575 2.00488 2.00404 2.00324 2.00247 2.00172 2.00100 2.00030 1.99962 1.99897 1.99834 1.99773 1.99714 1.99656 1.99601 1.99547 1.99495 1.99444 1.99394 1.99346 1.99300 1.99254 1.99210 1.99167 1.99125 1.99085 1.99045 1.99006 2.42080 2.41847 2.41625 2.41413 2.41212 2.41019 2.40835 2.40658 2.40489 2.40327 2.40172 2.40022 2.39879 2.39741 2.39608 2.39480 2.39357 2.39238 2.39123 2.39012 2.38905 2.38801 2.38701 2.38604 2.38510 2.38419 2.38330 2.38245 2.38161 2.38081 2.38002 2.37926 2.37852 2.37780 2.37710 2.37642 2.37576 2.37511 2.37448 2.37387 2.70118 2.69807 2.69510 2.69228 2.68959 2.68701 2.68456 2.68220 2.67995 2.67779 2.67572 2.67373 2.67182 2.66998 2.66822 2.66651 2.66487 2.66329 2.66176 2.66028 2.65886 2.65748 2.65615 2.65485 2.65360 2.65239 2.65122 2.65008 2.64898 2.64790 2.64686 2.64585 2.64487 2.64391 2.64298 2.64208 2.64120 2.64034 2.63950 2.63869 3.30127 3.29595 3.29089 3.28607 3.28148 3.27710 3.27291 3.26891 3.26508 3.26141 3.25789 3.25451 3.25127 3.24815 3.24515 3.24226 3.23948 3.23680 3.23421 3.23171 3.22930 3.22696 3.22471 3.22253 3.22041 3.21837 3.21639 3.21446 3.21260 3.21079 3.20903 3.20733 3.20567 3.20406 3.20249 3.20096 3.19948 3.19804 3.19663 3.19526 Tabel Distribusi t