6 BAB II KAJIAN TEORI
Pada bab ini akan dibahas mengenai beberapa definisi dan teori yang akan digunakan pada pembahasan berdasarkan literatur yang relevan.
A. Program Linear
Model Program Linear (MPL) merupakan salah satu model yang dapat digunakan untuk memodelkan masalah optimasi yang bertujuan memaksimumkan atau meminimumkan fungsi tujuan yang berbentuk linear dan memenuhi beberapa fungsi kendala yang juga berbentuk linear. MPL memiliki dua unsur utama yaitu fungsi tujuan dan fungsi kendala. Fungsi tujuan adalah fungsi linear dari beberapa variabel keputusan. Variabel keputusan adalah variabel yang menyatakan keputusan-keputusan yang akan dibuat. Variabel keputusan akan memberikan nilai fungsi tujuan yang paling menguntungkan. Variabel keputusan harus ditentukan terlebih dahulu sebelum menentukan fungsi tujuan dan fungsi kendala. Fungsi kendala adalah fungsi yang mengendalikan nilai variabel keputusan. Berikut ini diberikan contoh model program linear untuk lebih memahami yang dimaksud dengan fungsi tujuan dan fungsi kendala.
Contoh 2.1
Akan ditentukan nilai dari yang memaksimumkan
(2.1) dengan kendala (2.2)
7
Fungsi (2.1) merupakan fungsi tujuan dan Fungsi (2.2) merupakan fungsi kendala. Selanjutnya, Definisi 2.1 berikut menjelaskan tentang fungsi.
Definisi 2.1 Fungsi(Varberg dan Purcell, 2010:57). Sebuah fungsi f adalah suatu aturan korespondensi yang menghubungkan setiap obyek x dalam satu himpunan yang disebut daerah asal fungsi, dengan sebuah nilai tunggal f(x) dari himpunan kedua yang disebut daerah hasil fungsi.
Untuk lebih memahami definisi tentang fungsi, berikut ini diberikan contoh tentang fungsi.
Contoh 2.2
Gambar 2.1 dibawah ini merupakan contoh gambar bukan fungsi.
Gambar 2.1 Bukan Fungsi Gambar 2.2 dibawah ini merupakan contoh gambar fungsi.
Gambar 2.2 Fungsi a b c x y z 𝐴 𝐵 a b c x y z 𝐴 𝐵
8
Salah satu bentuk fungsi yaitu fungsi linear, berikut ini diberikan definisi fungsi linear.
Definisi 2.2 Fungsi Linear(Winston, 2004:55). Fungsi f( ) =
merupakan fungsi linear dengan merupakan koefisien dari .
Berikut ini, diberikan contoh mengenai bentuk fungsi linear dan fungsi non linear. Contoh 2.3
Diberikan fungsi sebagai berikut:
(2.3)
(2.4)
Fungsi (2.3) merupakan fungsi linear dan Fungsi (2.4) merupakan fungsi nonlinear.
1. Model Program Linear
Menurut B.Susanta (1994) Formula (1.1), (1.2), dan (1.3) dapat dituliskan dalam bentuk matriks sebagai berikut.
Akan menentukan yang memaksimumkan
(2.5)
dengan kendala:
(2.6)
(2.7)
dengan adalah matriks , adalah vektor kolom , adalah vektor kolom , dan adalah vektor baris .
9 [ ] (2.8) [ ] (2.9) [ ] (2.10) [ ] (2.11)
MPL banyak digunakan dalam menyelesaikan masalah-masalah pengalokasian sumber daya, seperti dalam bidang pemasaran, keuangan, personalia, administrasi dan bidang lainnya. Selain itu dengan kemajuan teknologi, maka proses perhitungan untuk menyelesaikan MPL sudah menggunakan komputer, terutama dalam mengahadapi persoalan yang memiliki variabel cukup banyak, yang apabila dilakukan perhitungan dengan cara biasa akan memakai waktu yang cukup lama.
Langkah awal yang diperlukan membuat MPL adalah perumusan model. Model merupakan tiruan suatu realitas, sedangkan perumusan model merupakan langkah untuk membuat peralihan dari realita ke model kualitatif. Menurut Ayu (1996), untuk merumuskan model suatu masalah optimasi kedalam bentuk MPL, harus dipenuhi syarat-syarat berikut:
a. Tujuan masalah tersebut harus jelas dan tegas. Tujuannya yaitu ingin mendapatkan keuntungan yang maksimal atau meminimumkan biaya produksi
b. Harus ada beberapa alternatif yang ingin dibandingkan. Misalkan kombinasi jumlah produksi dan keuntungan yang diperoleh
10
d. Fungsi tujuan dan fungsi kendala dapat dirumuskan secara kuantitatif e. Adanya keterkaitan peubah
Menurut Hillier & Liebermann (2010:36-41), selain syarat-syarat di atas juga terdapat beberapa asumsi yang harus dipenuhi yaitu:
a. Asumsi Proportionality (Kesebandingan)
Asumsi proportionality menyatakan bahwa perubahan pada variabel keputusan ( ) akan menyebar dalam proporsi yang sama terhadap fungsi tujuan
( ) dan juga kendalanya ( ). Misalnya, apabila variabel keputusan dinaikkan dua kali, maka secara proporsional (seimbang dan serasi) nilai-nilai fungsi tujuan dan kendalanya juga akan menjadi dua kali lipat.
b. Asumsi Divisibility (Pembagian)
Asumsi ini menyatakan bahwa nilai variabel keputusan yang dihasilkan oleh setiap aktivitas tidak harus berupa bilangan bulat, artinya nilai variabel keputusan berupa bilangan real. Apabila diinginkan solusi yang berupa bilangan bulat (integer) maka harus digunakan metode integer programming.
c. Asumsi Determistic/Certainty (Kepastian)
Asumsi ini menghendaki bahwa semua parameter yang terdapat dalam model program linear ( ) dapat diperkirakan dengan pasti dan bernilai tetap. Apabila nilai-nilai parameternya probabilistik, maka harus digunakan formulasi pemrograman masalah stokastik.
d. Asumsi Linearity (Linearitas)
Asumsi linearity menyatakan bahwa fungsi tujuan dan semua fungsi kendala harus dapat dinyatakan sebagai suatu fungsi linear. Suatu fungsi kendala
11
yang melibatkan dua variabel keputusan maka dalam diagram dimensi dua kendala tersebut akan berupa suatu garis lurus. Demikian juga apabila suatu kendala melibatkan tiga variabel menghasilkan suatu bidang datar dan kendala yang melibatkan variabel menghasilkan hyperplane dalam ruang berdimensi .
e. Asumsi Additivity (Aditivitas/ Penambahan)
Menurut B. Susanta (1994:12), asumsi ini menyatakan bahwa nilai parameter suatu kriteria optimasi (koefisien variabel keputusan pada fungsi tujuan) merupakan jumlah dari individu-individu dalam program linier. Misalnya, keuntungan total yang merupakan variabel keputusan, sama dengan jumlah keuntungan yang diperoleh dari masing-masing kegiatan ( ).
2. Penyelesaian Model Program Linear
MPL dengan dua variabel atau tiga variabel yang dapat disusutkan menjadi dua variabel dapat diselesaikan dengan menggunakan metode grafik. Untuk MPL yang memuat tiga variabel atau lebih dan tidak dapat disusutkan menjadi MPL dengan dua varibel dapat diselesaikan dengan menggunakan metode simpleks (B. Susanta, 1994:68).
Menurut Supranto (2009:97), metode simpleks merupakan suatu metode yang secara sistematis dimulai dari suatu penyelesaian layak basis (plb) awal ke plb lainnya dan dilakukan secara berulang (dengan jumlah ulangan yang terbatas) sampai diperoleh penyelesaian optimal. Pada setiap langkah metode simpleks akan menghasilkan suatu nilai dari fungsi tujuan yang selalu lebih baik (besar) atau sama dari langkah-langkah sebelumnya. Solusi untuk model program linear yang memenuhi Formula (2.6) dan (2.7) disebut penyelesaian layak (p.l) dan
12
penyelesaian layak yang mengoptimumkan Fungsi (2.5) disebut penyelesaian optimum (p.o) (B. Susanta, 1994:113).
Menurut B Susanta (1994:69-108) Langkah-langkah penyelesaian MPL menggunakan tabel simpleks sebagai berikut:
a. Mengubah soal ke dalam bentuk kanonik
Bentuk kanonik MPL memiliki ciri-ciri bahwa semua kendala harus berbentuk kanonik/persamaan dengan koefisien ruas kanan tidak negatif dan memiliki variabel basis pada setiap kendala utamanya. Berikut ini diberikan definisi bentuk kanonik.
Definisi 2.3 Bentuk Kanonik (B. Susanta, 1994:70). Bentuk kanonik MPL adalah model program linear dengan semua fungsi kendala utama berbentuk persamaan.
Sehingga setiap kendala utama yang berbentuk pertidaksamaan diubah terlebih dahulu menjadi persamaan dengan menyisipkan variabel pengetat yaitu variabel slack dan variabel surplus. Variabel slack adalah variabel yang berfungsi untuk menampung sisa kapasitas pada kendala yang berupa pembatas. Sedangkan variabel surplus adalah variabel yang berfungsi untuk menampung kelebihan nilai ruas kiri pada kendala yang berupa syarat. Variabel slack ditambahkan pada ruas kiri suatu ketaksamaan (≤) fungsi kendala dan variabel surplus ditambahkan pada ruas kiri suatu ketaksamaan ( ) fungsi kendala sehingga bentuk fungsi kendala menjadi:
∑ menjadi ∑ (2.12)
13
Selanjutnya dalam pembentukan bentuk kanonik untuk suatu fungsi kendala utama yang belum memiliki variabel basis perlu ditambahkan variabel artificial . Penambahan variabel slack, surplus dan artificial pada fungsi kendala utama mengakibatkan penambahan variabel-variabel tersebut pada fungsi tujuan. Koefisien ongkos untuk variabel slack dan surplus adalah nol dan variabel artificial adalah – dengan mewakili suatu bilangan yang sangat besar. Untuk lebih memahami bentuk kanonik, berikut ini diberikan contoh tentang bentuk kanonik.
Contoh 2.4
Bentuk kanonik dari Contoh 2.1 yaitu:
akan ditentukan nilai , , , yang memenuhi susunan kendala: + = 17 2 + = 15 ≥ 0 dan memaksimumkan Kejadian penyelesaian persamaan linear dapat dilihat dengan rank suatu matriks. Rank suatu matriks adalah ukuran terbesar dari matriks bagian dari yang determinannya tidak nol (B. Susanta, 1994:34). Rank matriks dilambangkan dengan Jelas bahwa
14
(2.14)
Suatu matriks bujursangkar disebut singular bila dan disebut tidak singular bila . Jadi bila tidak singular maka . Berdasarkan Formula (2.6) dengan cara menulis matriks , disusun
matriks |
|
| adalah matriks yang
dilengkapi dengan suku tetap di ruas kanan. Secara umum, menurut B. Susanta (1994:38) kejadian penyelesaian persamaan linear dapat ditandai dengan suatu rank matriks sebagai berikut:
1) Jika ) maka tidak ada penyelesaian.
2) Jika maka ada penyelesaian. Terdapat dua jenis penyelasaian yang dapat diperoleh dengan mengetahui banyaknya yaitu:
a) Untuk maka diperoleh penyelesaian banyak b) Untuk maka diperoleh penyelesaian tunggal
Berikut ini diberikan contoh banyaknya penyelesaian pada persamaan linear. Contoh 2.5
MPL pada Contoh 2.4 diketahui nilai dan sehingga banyaknya penyelesaian persamaan linear adalah penyelesaian banyak dengan banyaknya plb adalah .
b. Menyusun tabel simpleks
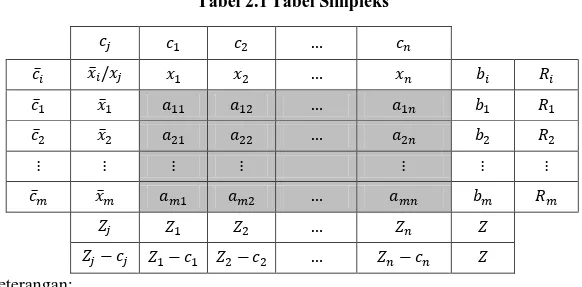
Untuk mempermudah langkah-langkah penyelesaikan MPL menggunakan metode simpleks, berikut ini diberikan bentuk umum tabel simpleks yang disajikan pada Tabel 2.1.
15
Tabel 2.1Tabel Simpleks
̅ ̅ ̅ ̅ ̅ ̅ ̅ ̅ Keterangan: : variabel-variabel keputusan : koefisien teknis
: koefisien ruas kanan : koefisien ongkos
̅ : variabel yang menjadi basis pada tabel yang ditinjau
̅ : koefisien ongkos dari variabel basis ̅ : ∑ ̅ (hasil kali ̅ dengan kolom ) : ∑ (hasil kali ̅ dengan )
: selisih dengan :
, dengan syarat
Masukan seluruh koefisien ongkos, koefisien teknis dan koefisien ruas kanan dari MPL bentuk kanonik ke dalam simpleks. Selanjutnya dengan membuat variabel non basis bernilai nol pada Tabel 2.1 akan diperoleh penyelesaian basis awal yaitu ̅ ̅ = dan penyelesaian basis ini dikatakan layak jika nilai penyelesaian lebih besar atau
16
sama dengan nol. Berikut ini akan diberikan contoh penyelesaian metode simpleks.
Contoh 2.6
Bentuk kanonik Contoh 2.5 dimasukkan kedalam Tabel 2.2 sebagai berikut. Tabel 2.2Tabel Awal Simpleks
12 -2M+2 M+3 -15M+76 -2M-3 M-2
Dari Tabel 2.2 dapat diketahui penyelesaian basis awal adalah
. c. Menguji keoptimuman
Langkah ini bertujuan untuk memeriksa penyelesaian awal basis yang diperoleh dari tabel simpleks. Suatu penyelesaian layak basis MPL telah optimum apabila untuk setiap , dengan . Apabila penyelesaian yang diperoleh dalam tabel simpleks telah optimum, maka langkah metode simpleks berhenti dan diperoleh penyelesaian yang optimum. Pada akhir iterasi (solusi akhir), variabel artificial harus bernilai nol. Saat variabel artificial ini mempunyai nilai yang tidak sama dengan nol, maka solusi yang diperoleh dinyatakan sebagai solusi tak layak. Namun apabila penyelesaian yang diperoleh belum optimum, maka dilanjutkan langkah
17
keempat yaitu memperbaiki tabel simpleks untuk memperoleh penyelesaian yang lebih baik yaitu penyelesaian yang mengoptimumkan fungsi tujuan. Pada Contoh 2.6 penyelesaian layak basis MPL belum optimum karena masih ada
.
d. Memperbaiki tabel simpleks
Langkah ini bertujuan untuk mencari penyelesaian layak basis lain yang akan menghasilkan penyelesaian yang lebih baik yaitu membuat nilai fungsi tujuan lebih besar dari tabel sebelumnya.
Tabel simpleks yang baru diperoleh dengan cara memilih salah satu variabel non basis untuk dijadikan variabel basis baru pada tabel simpleks baru yang akan dibuat dan memilih satu variabel basis yang akan keluar dari basis karena akan digantikan oleh variabel basis baru yang telah terpilih. Variabel non basis yang akan menjadi variabel basis fungsi tujuan adalah variabel non basis pada kolom ke-k yang memiliki nilai paling kecil (
). Selanjutnya kolom yang terpilih tersebut dinamakan kolom kunci. Apabila ada beberapa alternatif kolom kunci, maka dapat dipilih salah satu diantaranya secara acak yang nantinya akan menyebabkan tabel simpleks berputar (cycling) yaitu langkah-langkah simpleks yang akan terus berjalan.
Variabel basis yang harus keluar yaitu variabel basis yang memiliki nilai yang terkecil dengan
dan . Baris yang terpilih dinamakan sebagai baris kunci dan perpotongan unsur yang terdapat pada baris kunci dan kolom kunci dinamakan unsur kunci. Unsur kunci ini yang digunakan untuk memperbaiki tabel.
18
Tabel baru yang telah diperoleh, dilakukan kembali uji keoptimalan dengan melihat nilai Apabila penyelesaiannya telah optimal maka iterasi dihentikan, tetapi apabila penyelesaiannya belum optimal maka langkah selanjutnya ulangi kembali ke langkah ketiga. Penyelesaian optimum dapat dilihat di kolom bi. Sedangkan nilai optimal dari fungsi tujuan dapat dilihat di baris kolom bi.
Contoh 2.6 diketahui bahwa MPL belum optimum maka dilakukan perbaikan tabel yaitu dengan memilih nilai paling kecil. Nilai paling kecil pada Tabel 2.2 terdapat pada kolom 1 dan ditetapkan sebagai kolom kunci. Selanjutnya disusun nilai yang terlihat pada Tabel 2.3 di bawah ini.
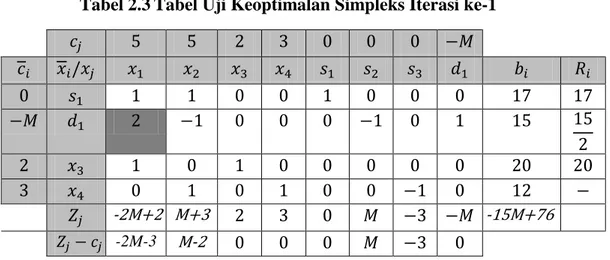
Tabel 2.3Tabel Uji Keoptimalan Simpleks Iterasi ke-1
Pada Tabel 2.3 masih ada nilai yang bernilai negatif yaitu kolom 1 dan kolom 7, jadi tabel belum optimum. Sesuai dengan langkah 4, dipilih kolom 1 sebagai kolom kunci dan disusun . Kemudian terkecil terdapat pada baris 2, berarti (basis ke-2) harus keluar digantikan oleh . Tabel perlu diperbaiki dan diperoleh seperti Tabel 2.4 berikut ini.
-2M+2 M+3 -15M+76 -2M-3 M-2
19
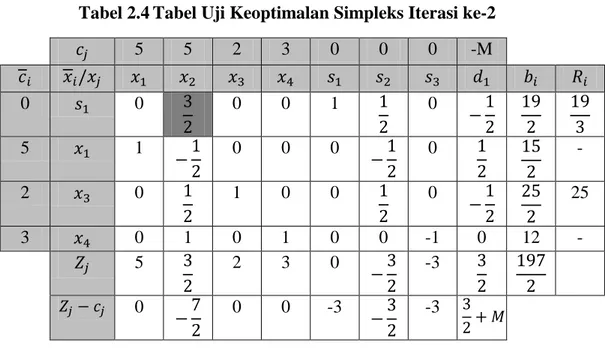
Tabel 2.4Tabel Uji Keoptimalan Simpleks Iterasi ke-2
5 5 2 3 0 0 0 -M 0 0 0 0 1 0 5 1 0 0 0 0 - 2 0 1 0 0 0 25 3 0 1 0 1 0 0 -1 0 12 - 5 2 3 0 -3 0 0 0 -3 -3
Diketahui bahwa Tabel 2.4 belum optimum sehingga dipilih kolom 2 sebagai kolom kunci dan disusun . Kemudian terkecil terdapat baris 1, berarti (basis ke-1) harus keluar digantikan dengan . Tabel perlu diperbaiki dan diperoleh seperti Tabel 2.5 berikut ini.
Tabel 2.5Tabel Uji Keoptimalan Simpleks Iterasi ke-3
20
Diketahui bahwa Tabel 2.5 belum optimum sehingga dipilih kolom 7 sebagai kolom kunci dan disusun . Karena nilai semua pada kolom kunci maka nilai tidak ada dan dapat disimpulkan bahwa penyelesaian layak berada di tak berhingga.
Selain kejadian-kejadian diatas terdapat juga kejadian-kejadian khusus dalam metode simpleks yaitu diantaranya:
a) MPL tidak layak yang disebabkan oleh penyelesaian optimum tidak memenuhi kendala yang dapat dilihat dari adanya penyelesaian optimum ada variabel artificial yang bernilai positif.
b) Merosot (degenerate) yang terjadi karena variabel basis dalam penyelesaian optimum bernilai nol.
c) Kendala berlebih (redundant) terjadi saat terdapat variabel pengetatdan
artificial merupakan variabel basis dalam penyelesaian optimum dan
bernilai tidak nol.
d) Ada alternatif PO (solusi lebih dari satu) yang terjadi karena pada penyelesaian optimum terdapat entri yang bukan variabel basis bernilai nol.
e) Solusi tunggal terjadi karena banyaknya entri sama dengan banyak basisnya.
f) Penyelesaian layak di tak berhingga saat semua koefisien pada kolom kunci bernilai negatif atau nol.
Masalah optimasi dapat diselesaikan dengan menggunakan Matlab Optimization Toolbox. Matlab Optimization Toolbox mempunyai subroutine atau
21
solver LINPROG untuk menyelesaikan MPL. Menurut Santoso (2008:82) MPL
(1.1), (1.2), dan (1.3) dapat diformulakan dengan bentuk sebagai berikut:
min
fungsi kendala
(2.15)
Sedangkan sintaks linprog dalam Matlab adalah
>>[x,fx,exitflag,out]=LINPROG (f,A,b,Aeq,beq,[ ],[ ],LB,UB)
dengan adalah koefisien untuk fungsi tujuan dan adalah matriks koefisien teknis dan adalah vektor koefisien ruas kanan untuk kendala yang berbentuk pertidaksamaan, dan masing-masing adalah matriks koefisien teknis dan vektor koefisien ruas kanan untuk kendala yang berbentuk persamaan, serta dan masing-masing batas bawah dan batas atas. Untuk batas bawah tidak terbatas maka dan batas atas tidak terbatas maka Berikut ini contoh dalam software Matlab untuk menyelesaikan MPL.
Contoh 2.7
Berdasarkan Contoh 2.1, fungsi tujuan tersebut harus diubah ke masalah minimasi dengan mengalikannya dengan -1 yaitu
[ ]
dan kendala yang berbentuk pertidaksamaan bisa diekspresikan sebagai berikut:
[ ] [ ] [ ] serta kendala yang berbentuk persamaanyaitu
22
[ ] [ ] [ ]
Setelah mengkonversikan fungsi tujuan menjadi minimasi, selanjutnya masalah diatas dapt diselesaiakn dengan LINPROG sebagai berikut:
>> f = [-5 -5 -2 -3] ;
>> A = [1 1 0 0; -2 1 0 0; 0 1 0 1] ; % koefisien teknis >> b = [ 17 -15 -12] ; % koefisien ruas kanan
>> Aeq = [1 0 1 0] ; % koefisien teknis yang berbentuk = >> beq = [20] ; % koefisien ruas kanan yang berbentuk = >> LB = [0 0 0 0] ; % nilai x yang nonnegatif
>> [X,fx,exitflag,output] = LINPROG (f,A b,Aeq,beq,[ ],[ ],LB) dari hasil output diketahui bahwa salah satu plb untuk MPL di atas
dan nilai fungsi tujuan
serta = -3. Fungsi tujuan yang sebelumnya diubah menjadi minimasi sehingga diperoleh fungsi tujuan bernilai negatif sehingga selanjutnya harus dikalikan dengan -1 untuk diperoleh nilai fungsi tujuan. Sebenarnya nilai , yaitu output ketiga dapat memberikan nilai salah satu dari berikut ini:
1. 1 jika solusi layak
2. 0 jumlah iterasi maksimum dicapai 3. -2 jika solusi tidak layak
23
5. -4 NaN ( )value encountered during execution of algorithm 6. -5 kedua primal dan dual problem infeasible
7. -7 arah pencarian (search) terlalu kecil, tidak bisa menuju titik yang lebih rendah lagi.
B. Konsep Himpunan Fuzzy 1. Pengertian Himpunan Fuzzy
Himpunan adalah kumpulan dari obyek-obyek tertentu yang tercakup dalam satu kesatuan dengan definisi (syarat) tertentu dan jelas. Himpunan klasik dapat didefinisikan dengan mendaftar anggota-anggota pada himpunan tersebut. Suatu anggota dalam suatu himpunan klasik mempunyai derajat keanggotaan
jika dan jika maka derajat keanggotaan = 0. Himpunan adalah himpunan „berbadan tinggi‟ yang didefinisikan sebagai Tinggi = . Dari definisi tersebut, dapat diketahui bahwa derajat keanggotaan orang yang memiliki tinggi 165 cm pada himpunan A,
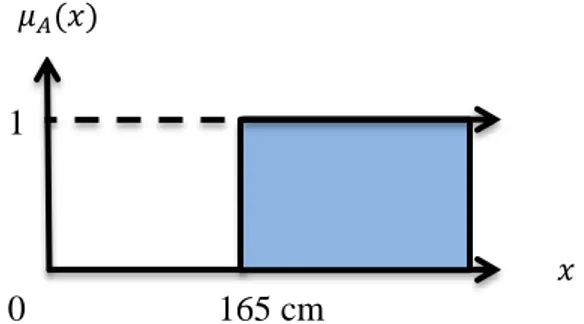
= 1 karena 165 A dan derajat keanggotaan orang yang memiliki tinggi 164 cm pada himpunan A, = 0 karena 164 A. Derajat keanggotaan di atas digambarkan menggunakan Gambar 2.3 sebagai berikut.
1
0 165 cm
Gambar 2.3 Grafik Himpunan “berbadan tinggi” 𝜇𝐴 𝑥
24
Himpunan fuzzy merupakan pengembangan lebih jauh dari konsep matematika tentang himpunan klasik. Menurut George J Klir, dkk (1997:6), teori himpunan fuzzy (fuzzy set) pertama kali diperkenalkan oleh Lotfi A. Zadeh pada tahun 1965, yaitu himpunan yang memiliki batas-batas keanggotaan himpunan yang tidak jelas. Keanggotaan pada himpunan fuzzy tidak dinyatakan dengan derajat keanggotaannya 0 atau 1, melainkan dengan derajat keanggotaan berupa bilangan real pada interval [0,1]. Adapun definisi dari himpunan fuzzy adalah sebagai berikut.
Definisi 2.4 (Zimmermann, 2001:11-12). Misalkan adalah koleksi dari
objek-objek yang dinotasikan dengan , suatu himpunan fuzzy ̃ dalam suatu himpunan
adalah suatu himpunan pasangan berurutan ̃ ̃ dengan
̃ adalah derajat keanggotaan x di ̃ yang nilainya pada rentang [0,1].
Menurut Zimmermann (2001:12-13) himpunan fuzzy dapat dinotasikan dengan dua cara, yaitu:
a. Himpunan fuzzy dituliskan sebagai pasangan berurutan, dengan elemen pertama menunjukkan nama elemen dan elemen kedua menunjukkan derajat keanggotaan.
̃ ̃ (2.16)
b. Himpunan fuzzy dinotasikan sebagai
̃ ̃ ̃ ...=∑ ̃ , jika diskrit (2.17) dan
25
̃ ∫ ̃ , jika kontinu (2.18)
Berikut ini diberikan contoh himpunan fuzzy. Contoh 2.8
Himpunan tinggi badan sekelompok orang dalam centimeter (cm) dinotasikan dengan .
Himpunan fuzzy “berbadan tinggi” dinotasikan dengan ̃ yang memiliki fungsi keanggotaan sebagai berikut:
̃ {
Sehingga ̃ dapat dinyatakan sebagai ̃ ={(140,0),(145,0.2),(150,0.4),(155,0.6), (160,0.8),(165,1.0)}.
Seperti himpunan klasik, himpunan fuzzy juga memiliki syarat yang dinyatakan dalam definisi berikut:
Definisi 2.5 (Ibrahim, 2004:35). Himpunan fuzzy kosong adalah himpunan fuzzy dengan derajat keanggotaan untuk semua elemen himpunan adalah 0.
Berikut ini diberikan contoh tentang himpunan fuzzy kosong. Contoh 2.9
Diberikan suatu himpunan dan sehingga
26
Definisi 2.6 (Ibrahim, 2004:35). Himpunan semesta fuzzy adalah himpunan fuzzy dengan derajat keanggotaan dari semua elemen himpunan adalah 1.
Berikut ini diberikan contoh tentang himpunan semesta fuzzy. Contoh 2.10
Diberikan dan sehingga ̃
merupakan himpunan semesta fuzzy.
Definisi 2.7 (Zimmermann, 2001:14). Himpunan α-cut ̃ adalah himpunan
(klasik) elemen-elemen yang ada pada himpunan fuzzy ̃ yang ̃ untuk
suatu nilai α [ ] yaitu:
̃ ̃ [ ]
Berikut ini diberikan contoh untuk lebih memahami definisi dari himpunan ̃ . Contoh 2.11
Diberikan dan ̃ (l,0.2), (2,0.5), (3,0.8), (4,1.0), (5,0.7), (6,0.3)}. Untuk ̃ ={1,2,3,4,5,6}, ̃ ={2,3,4,5}, ̃ ={3,4},
̃ ={4}.
Definisi 2.8 (Zimmermann, 2001:14). Support dari himpunan fuzzy ̃ yang
dinotasikan dengan S( ̃) adalah himpunan klasik dari dengan ̃
Berikut ini diberikan contoh untuk lebih memahami definisi S( ̃) Contoh 2.12
27
Definisi 2.9 (Ibrahim, 2004:36). Core ( ̃) adalah himpunan klasik dari semua
dengan derajat keanggotaan ̃ Contoh 2.13
Dari Contoh 2.11, Core ( ̃) adalah core dari himpunan fuzzỹ.
Definisi 2.10 (Ibrahim, 2004:36). Height ̃ dari himpunan fuzzy ̃ adalah
nilai tertinggi dari ̃ yang nilai α-level-nya tidak kosong.
Contoh 2.14
Berdasarkan Contoh 2.11, nilai , ̃ ={1,2,3,4,5,6} dengan ( ̃) adalah height dari himpunan fuzzỹ.
2. Jenis Fungsi Keanggotaan Fuzzy
Fungsi keanggotaan fuzzy adalah fungsi yang mengaitkan setiap elemen dengan suatu bilangan real dalam [0,1]. Fungsi keanggotaan menentukan derajat keanggotaan dari setiap elemen himpunan. Beberapa fungsi keanggotaan fuzzy yang dikenal antara lain fungsi linier (linier naik dan linier turun), fungsi segitiga, fungsi trapesium, fungsi bentuk bahu, fungsi kurva-S, fungsi bentuk lonceng/bell curve (kurva-PI, kurva Beta dan kurva Gauss).
Fungsi keanggotaan yang digunakan dalam penelitian ini adalah fungsi keanggotaan linear turun karena bentuk fungsi ini paling sederhana dan menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas.
Contoh 2.15
Jumlah persediaan minimal bahan baku gabah pada PB. Guyub Rukun untuk memproduksi beras slip tepat sebesar 100 ton dan dapat mengusahakan lagi
28
sebesar 20 ton. Suatu himpunan fuzzy sedikit ̃ dibentuk untuk menyatakan variabel jumlah persediaan bahan baku gabah yang digunakan untuk memproduksi beras slip dengan himpunan universal U=[100,20] dan fungsi keanggotaannya yaitu:
̃ {
Fungsi keanggotaan linear adalah fungsi pemetaan input ke derajat keanggotaanya yang digambarkan sebagai suatu garis lurus. Fungsi keanggotaan linear memiliki dua jenis yaitu:
a. Fungsi Keanggotaan Linear Naik
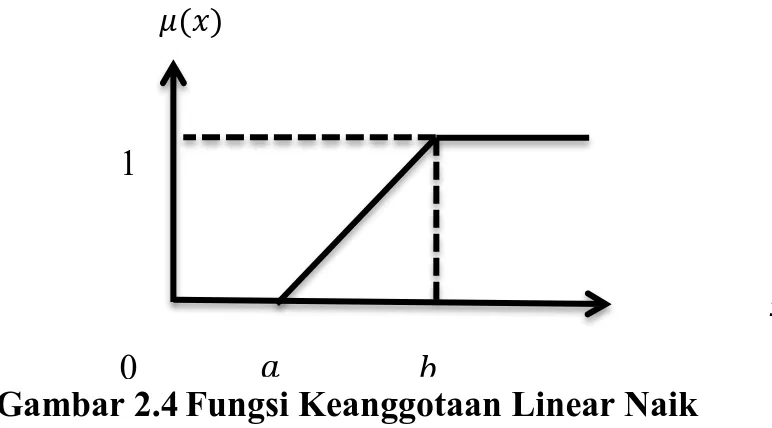
Fungsi keanggotaan linear naik memiliki representasi derajat keanggotaan 0 di ruas kiri dan bergerak ke kanan menuju derajat keanggotaan lebih tinggi atau 1. Menurut Kusumadewi (2002:31) Fungsi keanggotaan representasi linear naik sebagai berikut:
{ (2.19)
Himpunan fuzzy pada representasi linear naik direpresentasikan pada Gambar 2.4 di bawah ini.
Gambar 2.4Fungsi Keanggotaan Linear Naik 1
0 𝑎 𝑏
𝑥
29 Contoh 2.16
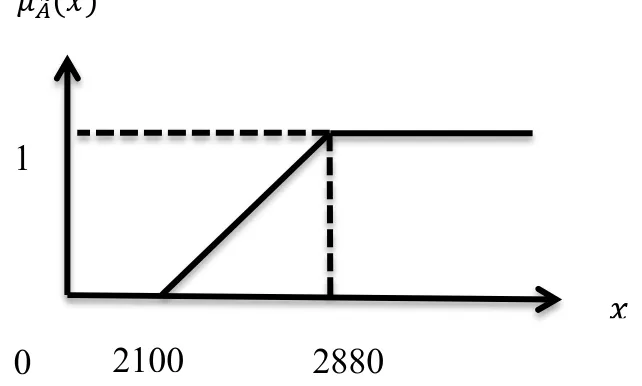
Himpunan fuzzy cepat ̃ pada variabel waktu yang digunakan untuk menggiling gabah dengan himpunan universal U=[2100,2880] yang mempunyai fungsi keanggotaan:
̃ {
jika
jika jika
Grafik representasi dari fungsi keanggotaan tersebut disajikan dalam Gambar 2.5 sebagai berikut.
Gambar 2.5Contoh Fungsi Keanggotaan Linear Naik
Berdasarkan fungsi keanggotaan di atas, dimisalkan untuk menentukan derajat keanggotaan waktu penggilingan gabah sebesar 2568 maka dilakukan perhitungan:
̃
dapat disimpulkan bahwa derajat keanggotaan waktu penggilingan sebesar 2412 adalah sebesar 0.6 pada himpunan fuzzy ̃.
b. Fungsi Keanggotaan Linear Turun
Fungsi keanggotaan linear turun merupakan kebalikan dari fungsi keanggotaan linear naik. Fungsi keanggotaan linear turun adalah fungsi
𝜇𝐴̃ 𝑥
1
0 2100 2880
30
keanggotaan yang memiliki derajat keanggotaan tertinggi atau satu [1] pada sisi kiri kemudian bergerak ke kanan menuju derajat keanggotaan yang lebih rendah atau nol [0]. Fungsi keanggotaan linear turun adalah sebagai berikut:
{ (2.20)
Menurut Kusumadewi (2002:32) Himpunan fuzzy pada representasi linear turun direpresentasikan pada Gambar 2.6 di bawah ini:
Gambar 2.6Fungsi Keanggotaan Linear Turun
Berikut ini diberikan contoh mengenai fungsi keanggotaan linear turun sebagai berikut:
Contoh 2.17
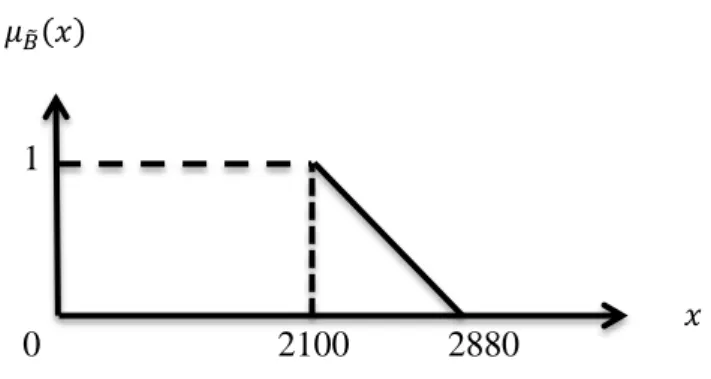
Himpunan fuzzy lambat ̃ pada variabel waktu yang digunakan untuk menggiling gabah dengan himpunan universal U=[2100,2880] yang mempunyai fungsi keanggotaan:
̃ { 𝑥 𝜇 𝑥 𝑎 𝑏
31
Grafik representasi dari fungsi keanggotaan tersebut disajikan dalam Gambar 2.7 sebagai berikut:
1
0 2100 2880
Gambar 2.7Contoh Fungsi Keanggotaan Linear Turun
Berdasarkan fungsi keanggotaan di atas, dimisalkan untuk menentukan derajat keanggotaan waktu penggilingan gabah sebesar 2458 maka dilakukan perhitungan:
̃
dapat disimpulkan bahwa derajat keanggotaan waktu penggilingan sebesar 2458 adalah sebesar 0.6 pada himpunan fuzzy ̃.
3. Bilangan Fuzzy
Konsep bilangan fuzzy muncul dalam kehidupan sehari-hari maupun dalam aplikasi teori fuzzy dalam bentuk besaran yang dinyatakan dengan bilangan yang tidak tepat, seperti misalnya “kira-kira 5 kilogram”, “sekitar 5 unit ” dan sebagainya. Secara intuitif dapat diterima bahwa ungkapan “kurang lebih 5”, “kira-kira 5 kilogram” atau “sekitar 5 unit” dapat dinyatakan dalam suatu himpunan fuzzy pada semesta bilangan real, dimana bilangan 5 mempunyai niali keanggotaan sama dengan 1 (satu), bilangan-bilangan di sekitar mempunyai derajat keanggotaan kurang dari 1 dan semakin jauh bilangan itu dari 5, derajat
𝑥 𝜇𝐵̃ 𝑥
32
keanggotaannya semakin mendekati 0 (nol) (Frans Susilo, 2006:111). Berikut diberikan definisi bilangan fuzzy:
Definisi 2.11 Bilangan Fuzzy (Klir & Yuan, 1995:97). Misalkan ̃ adalah
himpunan fuzzy pada . Bilangan fuzzy ̃ adalah himpunan fuzzy yang memenuhi
syarat-syarat sebagai berikut:
a. ̃ merupakan himpunan fuzzy normal
Himpunan fuzzy ̃ dalam normal jika terdapat sehingga .
b. ̃ merupakan interval tertutup untuk semua α [ ], dan
c. Support ̃ merupakan himpunan terbatas
Syarat bahwa ̃ merupakan interval tertutup untuk semua α [ ] sama dengan syarat bahwa ̃ merupakan himpunan konveks. Himpunan ̃ di adalah konveks jika
̃ ̃ ̃ dan setiap
[ ] (Nasseri,2008:1777). Bilangan fuzzy sebagai himpunan fuzzy normal dan konveks, serta untuk setiap merupakan interval tertutup. Jadi, bilangan fuzzy adalah himpunan konveks, normal, dan merupakan interval tertutup. (Chen dan Pham, 2000:42-43)
Bilangan fuzzy yang digunakan dalam tulisan ini adalah bilangan fuzzy linear turun yang memenuhi syarat fungsi keanggotaan linear sebagai berikut:
̃ {
(2.21)
Dimana adalah puncak nilai yang berarti bahwa derajat keanggotaanya adalah 1 dan adalah nilai persekitarannya dari . Bilangan fuzzy linear ditunjukkan dengan ̃ .
33 Contoh 2.18
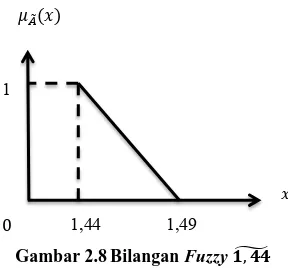
Untuk memproduksi 1 kuintal beras kristal biasanya diperlukan bahan baku gabah sebesar 1,44 kuintal. Akan tetapi pada musim-musim tertentu kadang terjadi serangan hama yang menyebabkan kualitas bahan baku gabah menurun sehingga untuk memproduksi 1 kuintal beras kristal diperlukan toleransi penambahan sebesar 0,05 kuintal. Sehingga jumlah jenis bahan baku gabah yang digunakan untuk memproduksi beras kristal merupakan bilangan fuzzy ̃ dan dapat dituliskan bahwa dan maka ̃ . Representasi bilangan fuzzy ̃ terlihat pada Gambar 2.8 yaitu
Gambar 2.8Bilangan Fuzzy ̃
Bilangan fuzzy ̃ bersifat normal, karena mempunyai derajat keanggotaan 1 untuk . Semua pada bilangan fuzzy ̃ tertutup pada selang
[ ]. Support dari himpunan fuzzy ̃ terbatas pada (1,44 , 1,49). Bilangan
fuzzy ̃ konveks karena untuk nilai dan dan
maka dengan ̃ ̃ ̃ sehingga ̃
̃ ̃ untuk setiap dan setiap [ ].
𝜇𝐴̃ 𝑥
1
1,44 1,49
34 4. Operasi pada Himpunan Fuzzy
Berikut ini penjelasan mengenai operasi himpunan fuzzy yang berupa irisan dan gabungan.
Definisi 2.12 Irisan Himpunan Fuzzy (Bellman & Zadeh, 1970:144). Irisan dari
dua himpunan fuzzy ̃ dan ̃ dinotasikan sebagai ̃ ̃ dan didefinisikan
sebagai himpunan fuzzy terbesar yang terdapat pada ̃ dan ̃. Fungsi
keanggotaan ̃ ̃ diberikan oleh
̃ ̃ ̃ ̃
Berikut ini diberikan contoh untuk lebih memahami definisi irisan himpunan fuzzy.
Contoh 2.19
Diberikan himpunan fuzzy ̃ ̃ yang didefinisikan sebagai berikut:
̃ ̃
untuk mencari ̃ ̃, terlebih dahulu menghitung ̃ ̃ untuk setiap . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . Jadi, ̃ ̃
35
Definisi 2.13 Gabungan Himpunan Fuzzy (Bellman & Zadeh, 1970:145).
Gabungan dari dua himpunan fuzzy ̃ dan ̃ dinotasikan sebagai ̃ ̃ dan
didefinisikan sebagai himpunan fuzzy terkecil yang terdapat pada ̃ dan ̃.
Fungsi keanggotaan ̃ ̃ diberikan oleh
̃ ̃ ̃ ̃
Berikut ini diberikan contoh untuk lebih memahami definisi gabungan himpunan fuzzy.
Contoh 2.20
Berdasarkan Contoh 2.19, untuk mencari ̃ ̃, terlebih dahulu menghitung
̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . ̃ ̃ ̃ ̃ . Jadi, ̃ ̃ .
C. Program Linear Fuzzy
Program linear menurut Amit Kumar, dkk (2010:37) merupakan salah satu teknik dalam riset operasi yang paling sering diterapkan. Nilai-nilai parameter model program linear harus terdefinisi dengan baik (tegas), sedangkan dalam
36
kehidupan nilai-nilai parameter yang tegas bukan merupakan asumsi yang realistis. Oleh karenanya penggunaan parameter dalam model program linear direpresentasikan dengan bilangan-bilangan fuzzy.
Menurut Klir & Yuan (1995:410), bentuk umum model program linear
fuzzy sama dengan bentuk umum model program linear biasa. Dalam program
linear fuzzy akan dicari suatu nilai yang merupakan fungsi tujuan yang akan dioptimasikan sedemikian hingga tunduk pada batasan-batasan yang dimodelkan dengan menggunakan himpunan fuzzy.
Bentuk matematika dari program linear fuzzy adalah: Maksimumkan: ∑ ̃ (2.22) dengan kendala ∑ ̃ ̃, i = 1,2, ... , m 0 , j = 1,2, ... , n
dengan ̃ ̃ dan ̃ semuanya adalah bilangan fuzzy.
Menurut Klir & Yuan (1995:410-411) program linear fuzzy memiliki dua kasus yaitu program linear fuzzy dengan hanya koefisien ruas kanan ( ) berbentuk bilangan fuzzy dan program linear fuzzy dengan koefisien teknis ( ) dan koefisien ruas kanan ( ) berbentuk bilangan fuzzy. Dalam penelitian ini akan dibahas mengenai program linear fuzzy dengan koefisien teknis dan koefisien ruas kanan berbentuk bilangan fuzzy linear turun dengan fungsi tujuan tidak fuzzy (tunggal).
37
Menurut Klir & Yuan (1995:411), bentuk umum dari program linear fuzzy
dengan koefisien teknis ( ) dan koefisien ruas kanan ( ) berbentuk bilangan fuzzy ini adalah sebagai berikut:
Maksimumkan: ∑ (2.23) dengan kendala ∑ ̃ ̃, i = 1,2, ... , m 0 , j = 1,2, ... , n
Bilangan linear turun fuzzy yang direpresentasikan dengan untuk a adalah puncak nilai yang berarti bahwa derajat keanggotaannya adalah satu dan d adalah nilai persekitarannya dari a yang dituliskan pada koefisien teknis ( ̃ ) sehingga ( ̃ dan koefisien ruas kanan ( ̃ dimisalkan dengan
untuk b adalah puncak nilai yang berarti bahwa derajat keanggotaannya adalah satu dan p adalah nilai persekitarannya dari b yang dituliskan pada koefisien ruas kanan ( ̃ Sehingga model program linear fuzzy dengan koefisien teknis ( ̃ ) dan koefisien ruas kanan ( ̃) berbentuk bilangan linear turun fuzzy dapat diformulasikan sebagai berikut:
Maksimumkan: ∑ (2.24) dengan kendala ∑ , i = 1,2, ... , m
38
0 , j = 1,2, ... , n
Dalam teori pengambilan keputusan fuzzy dikenal 3 konsep dasar (Bellman & Zadeh, 1970:147-149) yaitu fuzzy goal, fuzzy constraints, dan fuzzy decisions. Misalkan adalah himpunan yang memuat solusi dari pengambilan keputusan.
Fuzzy goal adalah himpunan fuzzy pada yang keanggotaannya didefinisikan
melalui fungsi keanggotaan:
: [ ]
Fuzzy constraint adalah himpunan fuzzy pada yang keanggotaannya
didefinisikan melalui fungsi keanggotaan: µC [ ]
Fuzzy decision adalah himpunan fuzzy yang merupakan irisan fuzzy
goal dan fuzzy kendala , yaitu dengan fungsi keanggotaan:
(2.25)
Contoh 2.21
Misalkan dimiliki fuzzy goal dan fuzzy constraint sebagai berikut:
µG { {
39 { ,jika ( ) ,jika ( ),jika min(1, 20 10 ) ,jika , jika (2.26)
Keputusan maksimal didefinisikan sebagai berikut:
= µG (x), µC (x)}. (2.27) Lebih umum, fuzzy decision hasil dari k fuzzy goal dan fuzzy kendala didefiinisikan oleh
. (2.28)
Dengan fungsi keanggotaan:
= { , . (2.29) Keputusan maksimal didefinisikan sebagai: